Image source: Do it! 딥러닝 교과서. 이지스 퍼블리싱 저
출력 계층의 역할은 네트워크가 수행해야 하는 작업을 완료하기 위해 기능에서 일부 추가 변환을 제공하는 것이다.
- feedforward network가 hidden features h = f(x; Θ) 를 제공한다고 가정하자.
- h → output units → y^
linear / sigmoid / softmax 가 주로 사용된다.
-
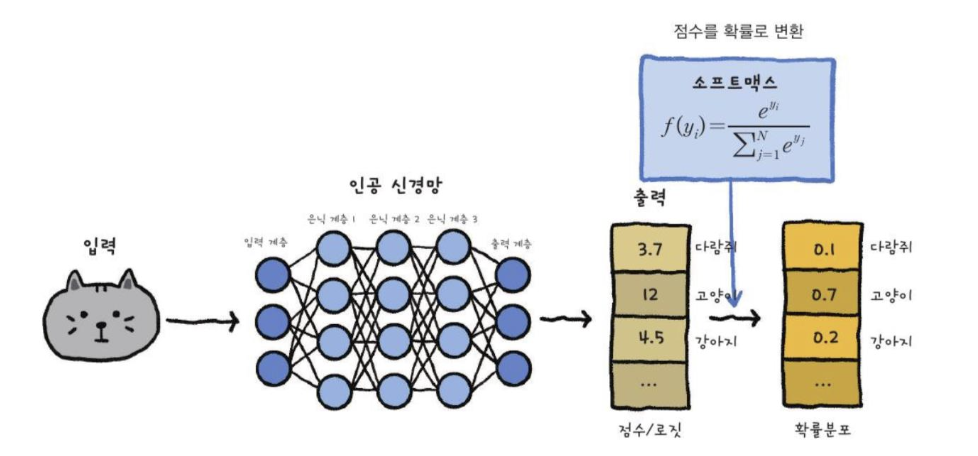
softmax: K 클래스에 대한 확률 분포를 나타낸다.
-
베르누이: sigmoid = 멀티누이: softmax
-
베르누이: 동전 던지기(2가지 경우의 수: 0 or 1), 이진 분류
-
멀티누이: 주사위 던지기(K가지 경우의 수: 1~K), 다중 분류
-
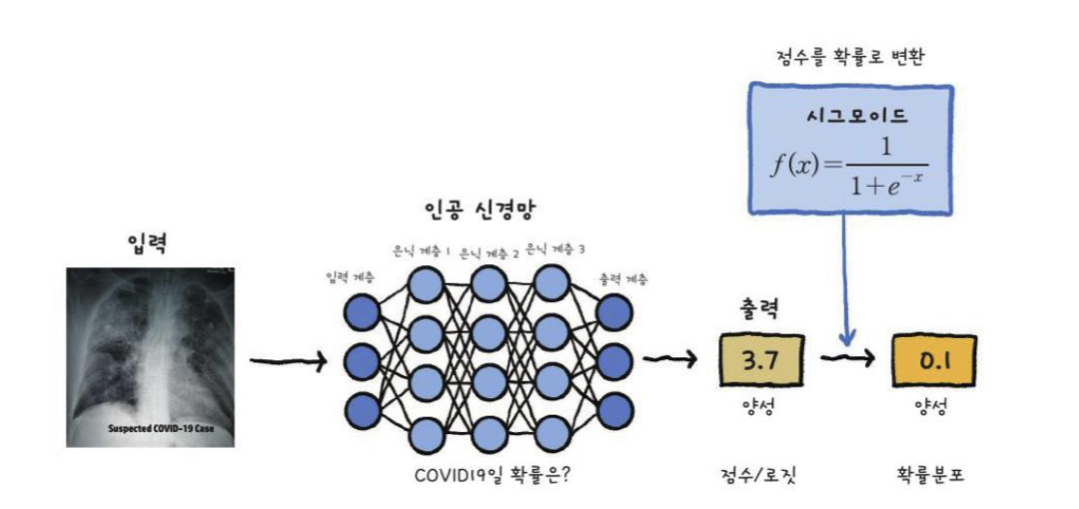
Linear Units for Gaussian Output Distributions
feature h가 주어졌을 때, 선형 output units은 y^ = 𝐰𝑇𝒉 + 𝑏를 생산한다.
- 주로 조건부 가우시안 분포의 평균을 생성하는데 사용된다.
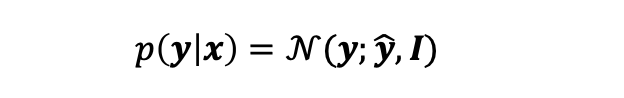
- log-likelihood의 최대화 == mean squared error(평균 오차 제곱)의 최소화
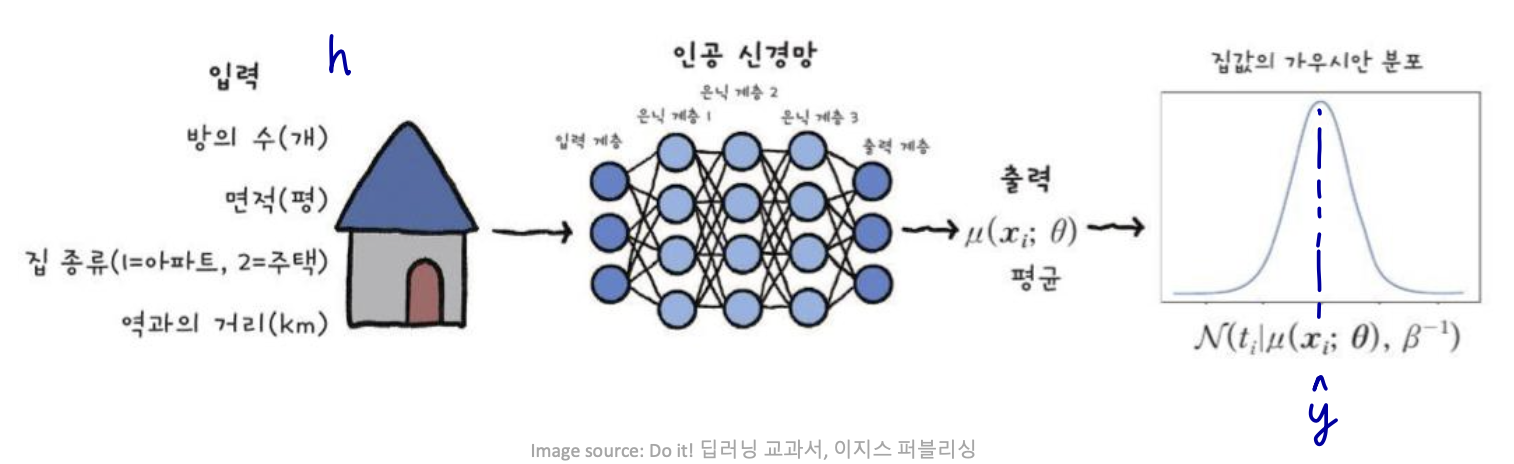
Sigmoid Units for Bernoulli Output Distributions
-
이진 변수 y 값 예측
-
이진 분류
-
y^ = P(y=1 | X)
-
x 일때 y=1일 확률
-
-
Threshold(임계값)?
-
P(y=1 | x) = max{ 0, min{1, 𝐰𝑇𝒉 + 𝑏 }}
-
𝐰𝑇𝒉 + 𝑏가 단위 간격을 벗어나면, gradient(기울기)가 0이 된다.
-
-
Sigmoid output
-
y^ = σ(𝐰𝑇𝒉 + 𝑏)
-
z = 𝐰𝑇𝒉 + 𝑏
-
z를 확률로 변환한다.
-
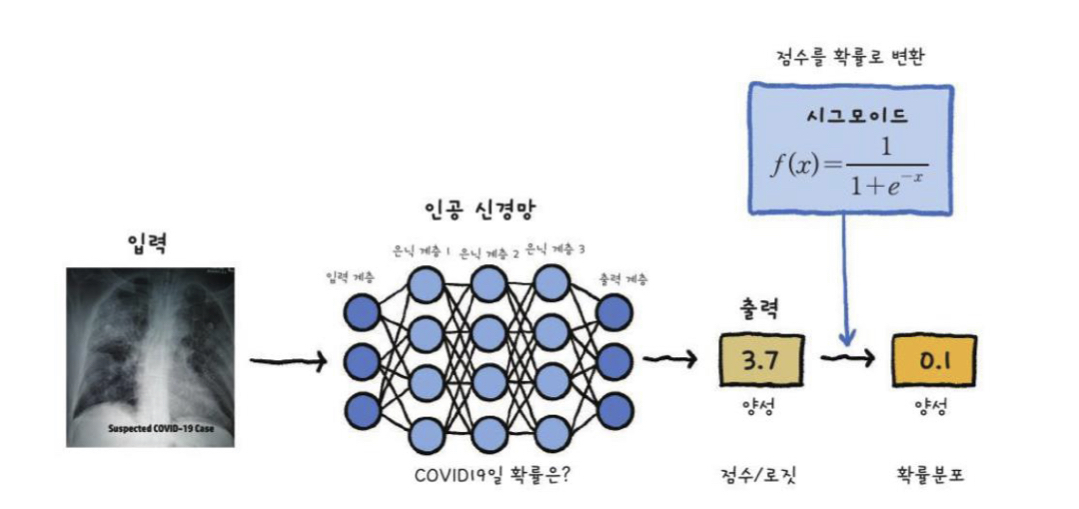
Softmax Units for Multinoulli Output Distributions
n개의 가능한 값을 가진 이산 변수에 대한 확률 분포를 나타낸다.
(*이산 변수: 하나하나 셀 수 있는 변수. e.g.) 한 회사의 직원 수)
소프트맥스 함수는 output classifier로써 가장 자주 사용된다.
-
sigmoid 함수의 일반화이다.
-
확률분포로 각 클래스가 나올 확률 값의 합이 1이 되도록 만들어준다.
Hidden Units
-
Hidden Units (은닉층)
-
input x의 벡터를 받는다.
-
affine 변환 계산. 𝒛 = 𝑾T𝒙 + 𝒃
-
노드별 비 선형 함수 적용 g(z)
-
-
은닉층은 활성화 함수 g(z)의 선택으로 서로 구별된다.
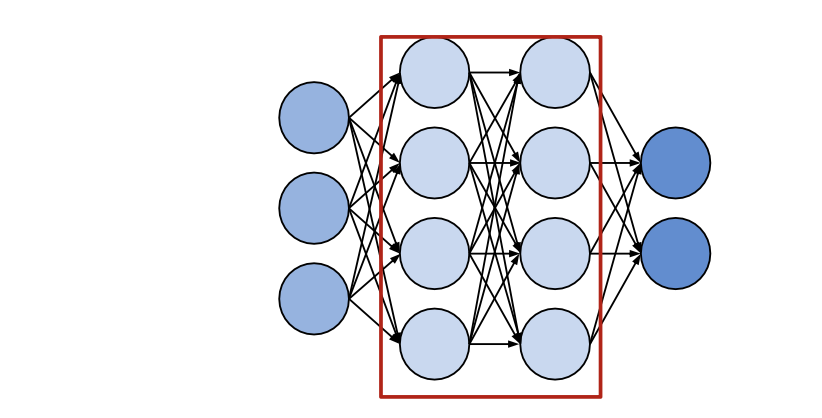
활성화 함수로 무엇을 사용할지 생각해야한다.
Activation Functions
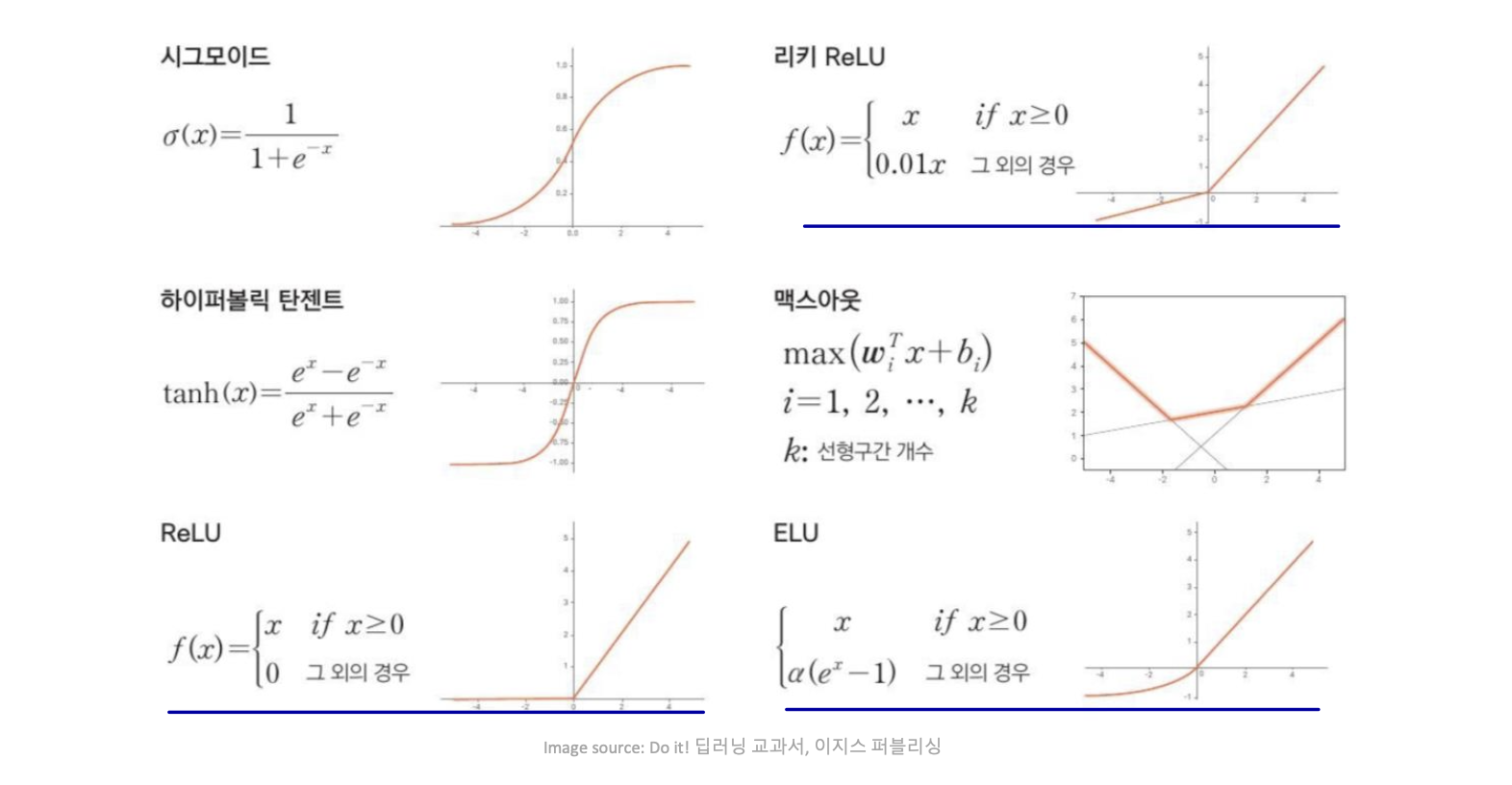
요즘은 밑줄 친 세 함수를 가장 자주 사용한다.
Rectified Linear Units (ReLU)
-
g(z) = max{0, z}
-
ReLU는 일반적으로 아핀 변환 위에 사용된다.
(*아핀 변환: 원점이 존재하지 않는 벡터 공간)
-
h = g(𝑾T𝒙 + 𝒃)
-
b의 모든 요소를 작은 양수값으로 설정
-
-
양수 영역에 포화 없음 / 계산적으로 매우 효율적임 / 빠른 수렴
-
활성화가 0인 경우 그래디언트 기반 방법을 통해 학습할 수 없다.
ReLU generalizations
-
ReLU의 한계 극복
-
절댓값 보정: g(z) = |z|
-
Leaky ReLU: g(z) = max{z, az} (fixed a)
-
Parametric ReLU: g(z) = max{z, az} (learnable a)
-
Exponential ReLU:
-
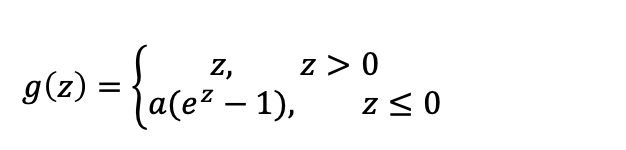
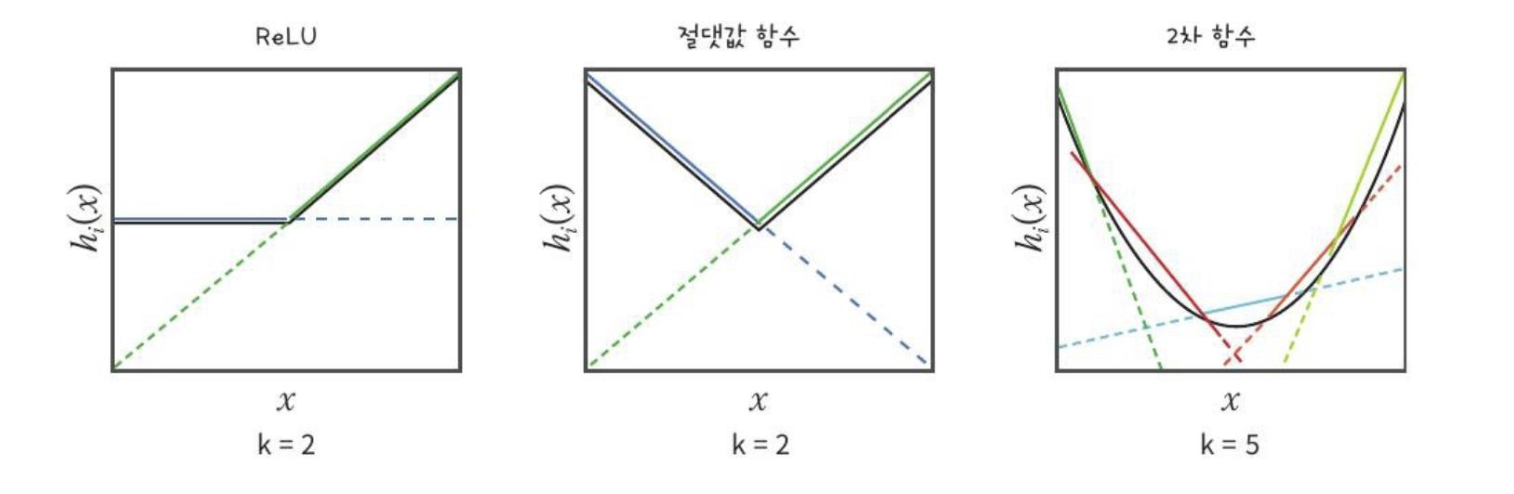
Maxout – further generalization of ReLU
-
Maxout 단위는 𝒛를 𝑘 값의 그룹으로 나눈다.
-
활성화 함수 자체 학습
-
충분히 큰 𝑘을 가진 모든 볼록 함수를 근사화할 수 있다
-
더 많은 매개변수와 뉴런이 필요하다.
-
Sigmoid and tanh
ReLU가 도입되기 전에는 대부분의 신경망이 시그모이드 또는 tanh 활성화 함수를 사용했다.
-
ouput range [0,1] 또는 [-1,1]
-
sigmoid: g(z) = σ(z) / tanh: g(z) = tanh(z)
-
tanh(𝑧) = 2𝜎(2𝑧) − 1이기 때문에 밀접하게 관련됨
-
𝑧가 큰 값의 양수이거나 음수일 때 포화 → 그래디언트 기반 학습을 매우 어렵게 만든다.
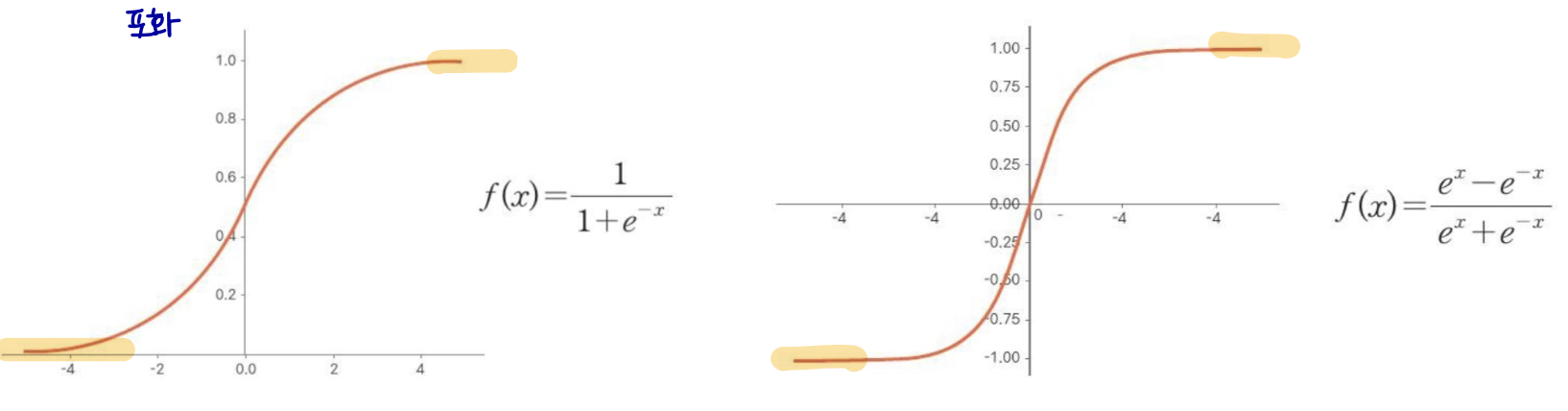
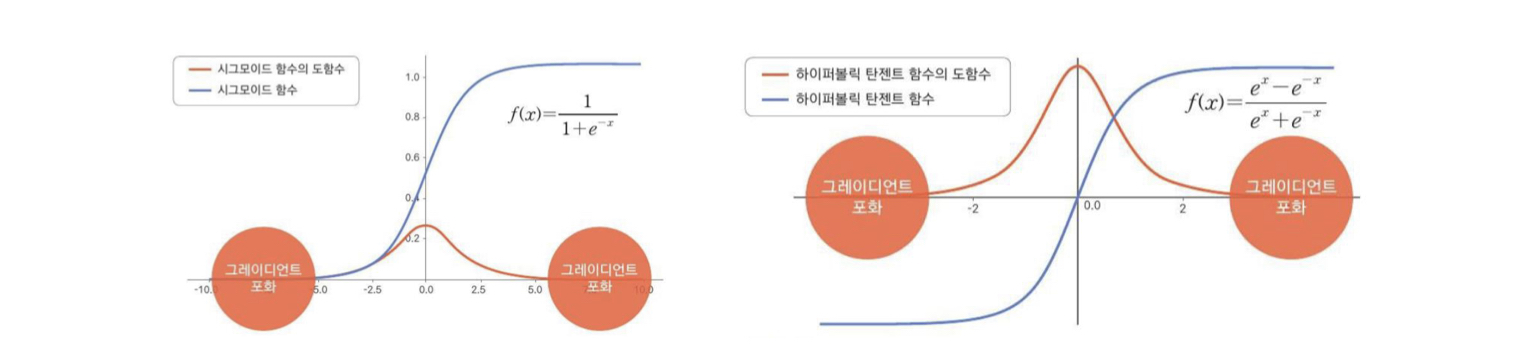
Sigmoid and tanh (cont.)
feedforward 네트워크에서 hidden units으로 사용되는 것은 이제 권장되지 않는다.
-
포화가 gradient를 죽인다 → 사라지는 gradient (기울기 0에 수렴 ..)
-
사용해야될 경우에는 tanh가 sigmoid보다 성능이 좋다,
-
zero-centered
-
0 근처에서 y=x 함수와 비슷하다.
-
One-side input slows down optimization
one-side input일 경우 입력이 모두 양수이거나 음수이기 때문에 가중치 업데이트 허용 방향이 1사분면과 3사분면으로 제한되어 학습경로가 진동하여 최적화가 느려질 수 있다.
최적해를 찾을 때 학습경로가 심하게 진동하는 이유는 경사하강법에서 발생할 수 있는 문제 중 하나인 plateau 문제이다. plateau는 함수의 기울기가 거의 0에 가까워져서 sgd가 최적화 과정에서 수렴하지 않고 심하게 진동한다. 이러한 문제는 함수의 극솟값 근처에서 흔히 발생한다.
이러한 문제를 해결하기 위해서 전처리 과정에서 zero-centering을 할 수 있다.