Feedforward Networks
전형적인 딥러닝 모델
- 심층 feedforward network, MLP
머신러닝 실무자에게 매우 중요
- 많은 중요한 상용 응용 프로그램의 기초
- e.g.) convolutional networks, recurrent networks
목표: approximating some function f*.
-
e.g.) classifier y = f*(x) maps an input x to a category y
-
feedforward network는 다음과 같이 정의 된다.
-
y = f*(x; Θ), 최적의 함수 근사치를 만들어내는 파라메터 Θ의 값을 학습한다.
(f*: 이상적인 함수 모델)
Feedforward Networks (cont.)
𝒙에서 출력 𝒚까지 함수를 통해 정보가 흐르기 때문에 'feedforward'라고 한다.
- x → f → y
forward propagation: input x가 초기 정보를 제공하고 각 층의 hidden units까지 전파한다. 그리고 마침내 y^ 결과 값을 생산해낸다.
모델의 아웃풋이 스스로 뒤로 가는 피드백 커넥션이 없다. (뒤에서 다시 앞으로 가는 경우 x)
- c.f.) recurrent neural networks (반례, feedback에 따라 재귀적으로 이전으로 감)
일반적으로 다양한 함수를 구성하여 표현되기 때문에 ‘network’라고 부른다.
- 모델은 유향 비순환 그래프와 연결된다.

Preliminary

Preliminary (cont.)

뉴런은 각 input과 가중치가 곱해진 값을 전부 더해 activation 함수에 넣어 ouput을 생성한다.
**Architecture & Notation**
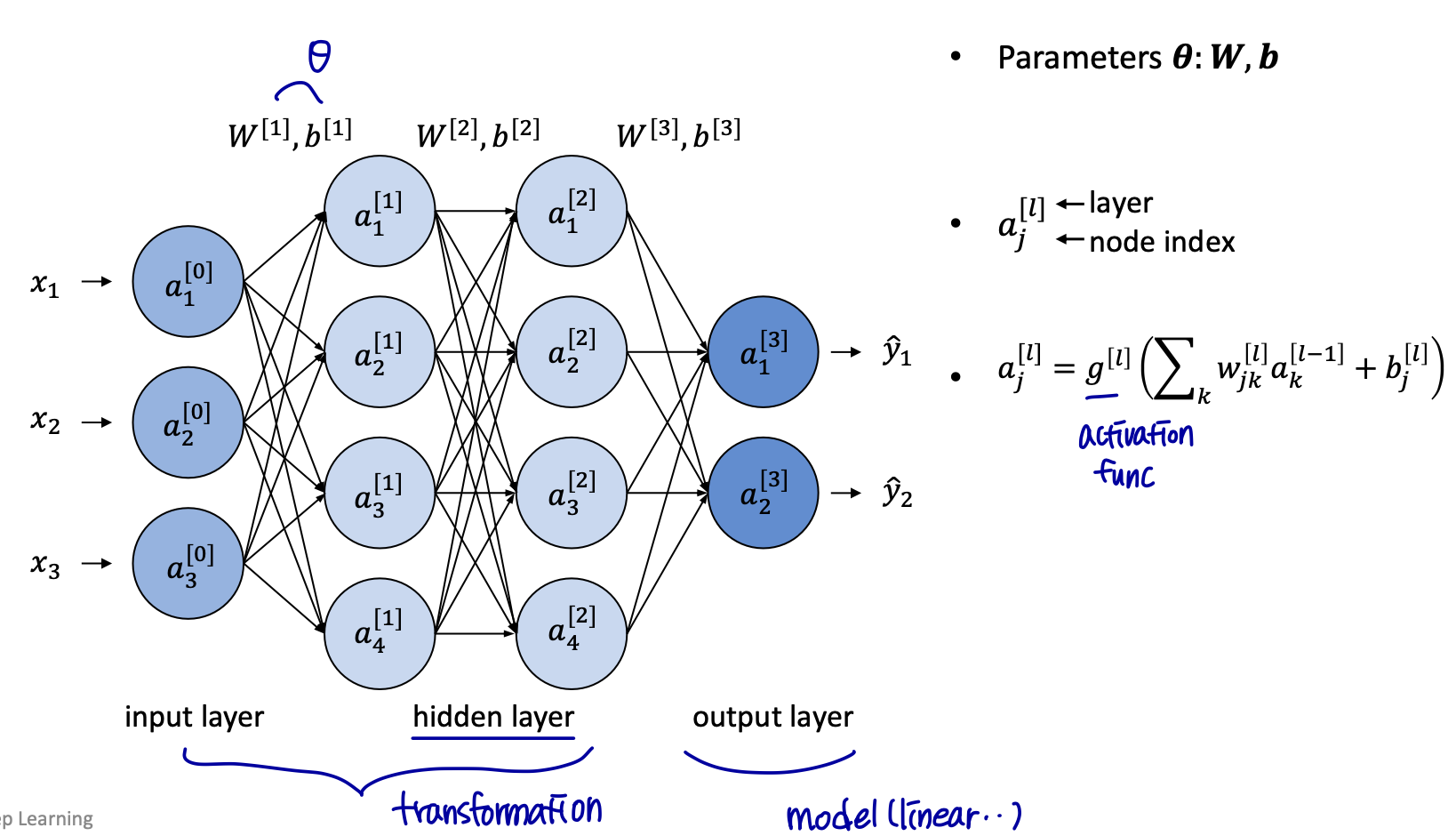
y = f*(x; Θ), 최적의 함수 근사치를 만들어내는 파라메터 Θ의 값을 학습한다.
- 이때 Θ는 w와 b (가중치와 편향값이다.)
Training

training을 통해 이상적인 모양에 맞는 f(x)를 찾아간다.
학습 알고리즘은 원하는 출력을 생성하기 위해 이러한 계층(=other layers)을 사용하는 방법을 결정해야 한다.
-
other layers: called hidden layer (트레이닝 데이터는 이러한 계층에 대해 원하는 출력을 표시하지 않는다.)
-
우리가 값을 찾아내야 된다는 의미에서 hidden layer라고 부른다.
Backpropagation
심층 신경망을 학습하는데 유용하게 활용되는 역전파(Backpropagation) 알고리즘도 경사하강법을 이용한다.
비용 정보는 gradient를 계산하기 위해 네트워크를 통해 역방향으로 흐른다.
체인 rule에서의 중간 항의 중복 계산을 피하기 위해 한 번에 한 레이어씩 기울기를 계산하고 마지막 레이어에서 역방향으로 반복한다.

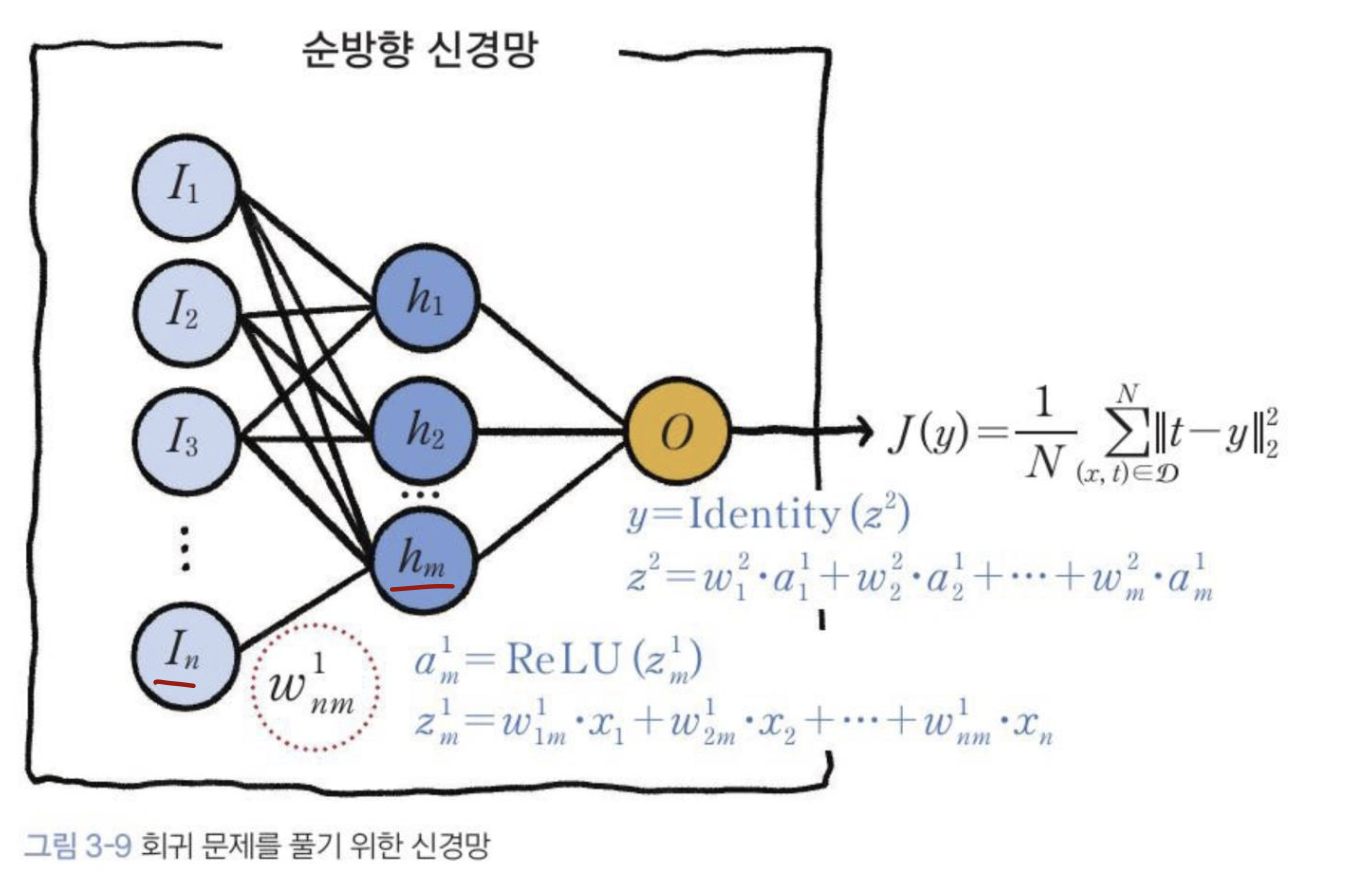
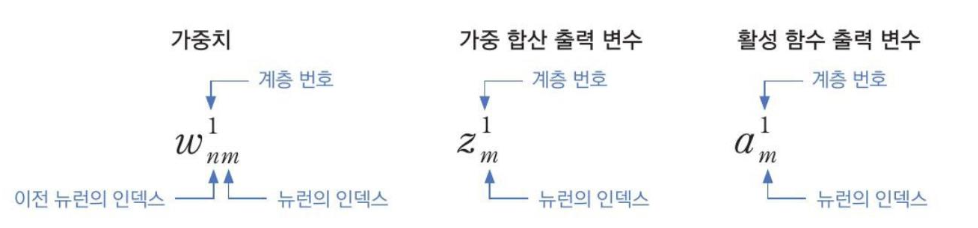
이 구조에서 적용되는 활성화 함수는 ReLU 함수 이다.
다층 퍼셉트론은 비용함수의 최소값을 찾아가는 방법으로 경사하강법을 활용한다. 각 층에서 가중치를 업데이트하기 위해서는 결국 각 층에서의 비용함수의 미분값이 필요하다.
이를 매우 효율적으로 해결하기 위한 방법이 역전파 알고리즘이다.
역전파란 역방향으로 오차를 전파시키면서 각 층의 가중치를 업데이트하고 최적의 학습 결과를 찾아가는 방법이다.
순전파에 있어서 가중치의 값을 매우 미세하게 변화시키면 비용함수 J1, J2도 매우 미세하게 변화한다.
이런 원리에 의해 순전파를 통해 출력층에서 계산된 오차 J1, J2의 각 가중치에 따른 미세변화를 입력 방향으로 역전파시키면서 가중치를 업데이트하고, 또 다시 입력값을 이용해 순전파시켜 출력층에서 새로운 오차를 계산하고, 이 오차를 또 다시 역전파시켜 가중치를 업데이트하는 식으로 반복한다.
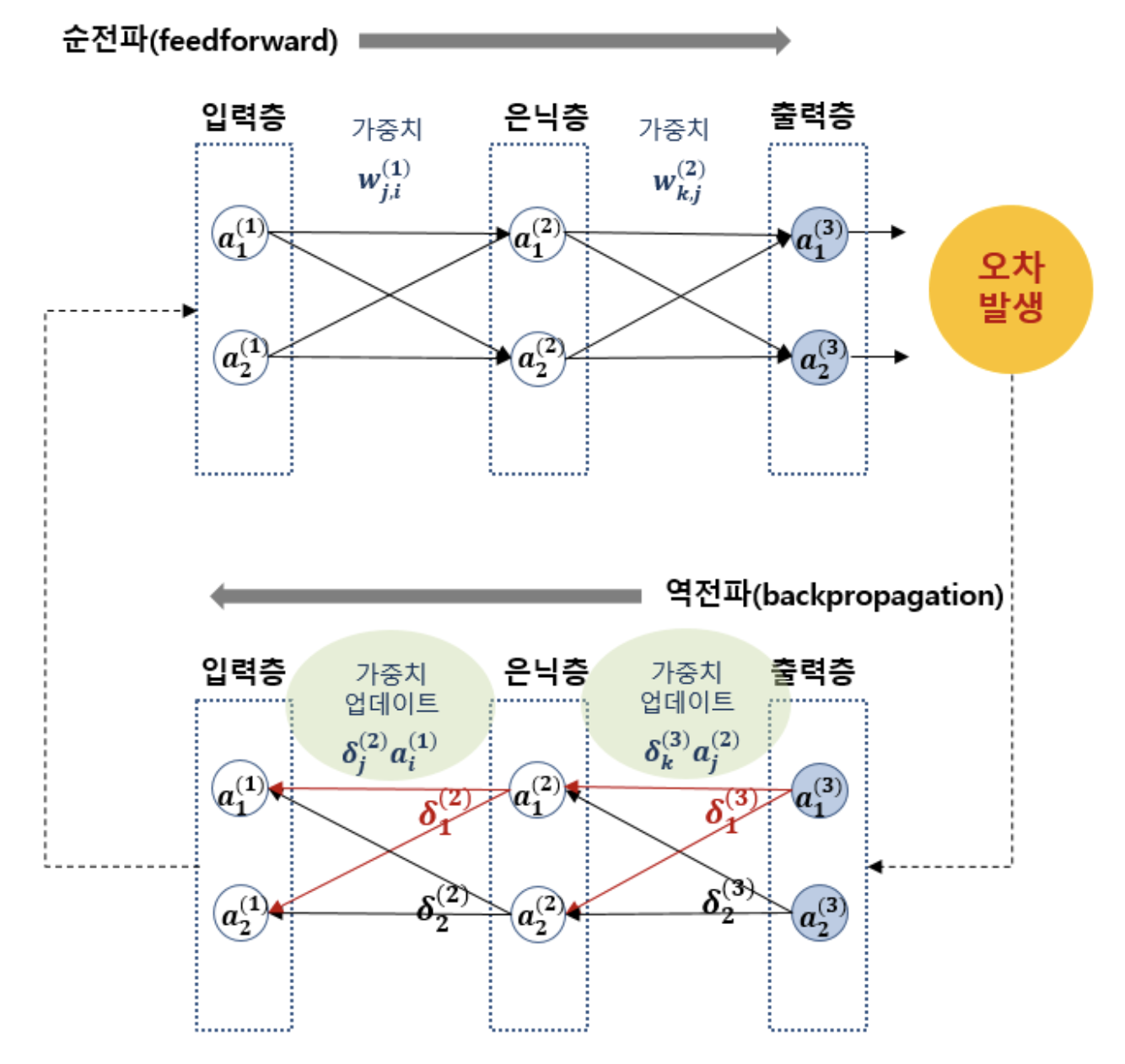
-
주어진 가중치 값을 이용해 출력층의 출력값을 계산한다 (feedforward)
-
오차를 각 가중치로 미분한 값을 기존 가중치에서 빼준다 (경사하강법 적용, backpropagation을 통해 이루어짐)
-
2번 단계는 모든 가중치에 대해 이루어진다
-
1~2번 단계를 주어진 학습횟수만큼 또는 주어진 허용오차값에 도달할 때까지 반복한다
2번 단계의 가중치 업데이트 식을 수식으로 표현하면 다음과 같다.
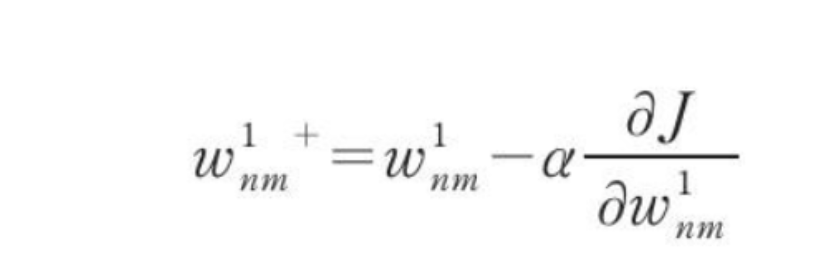
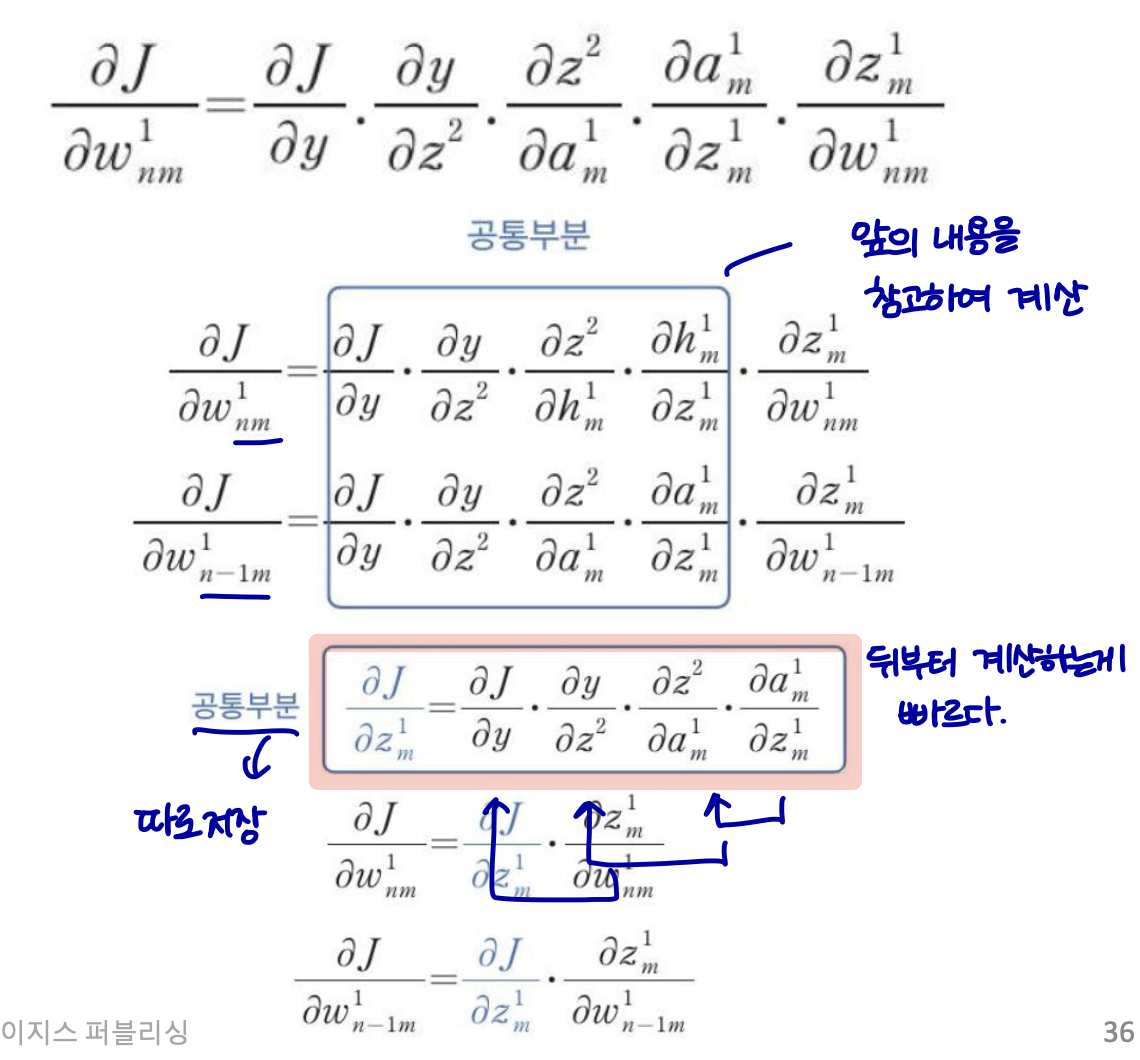
chain rule에 의해 오차의 가중치에 대한 미분값은 이와 같이 표현된다.
지금까지 기본적인 feedforward(순전파)와 backpropagation(역전파)의 개념을 살펴보았다.
이제 역전파의 간단한 예시를 살펴보자.
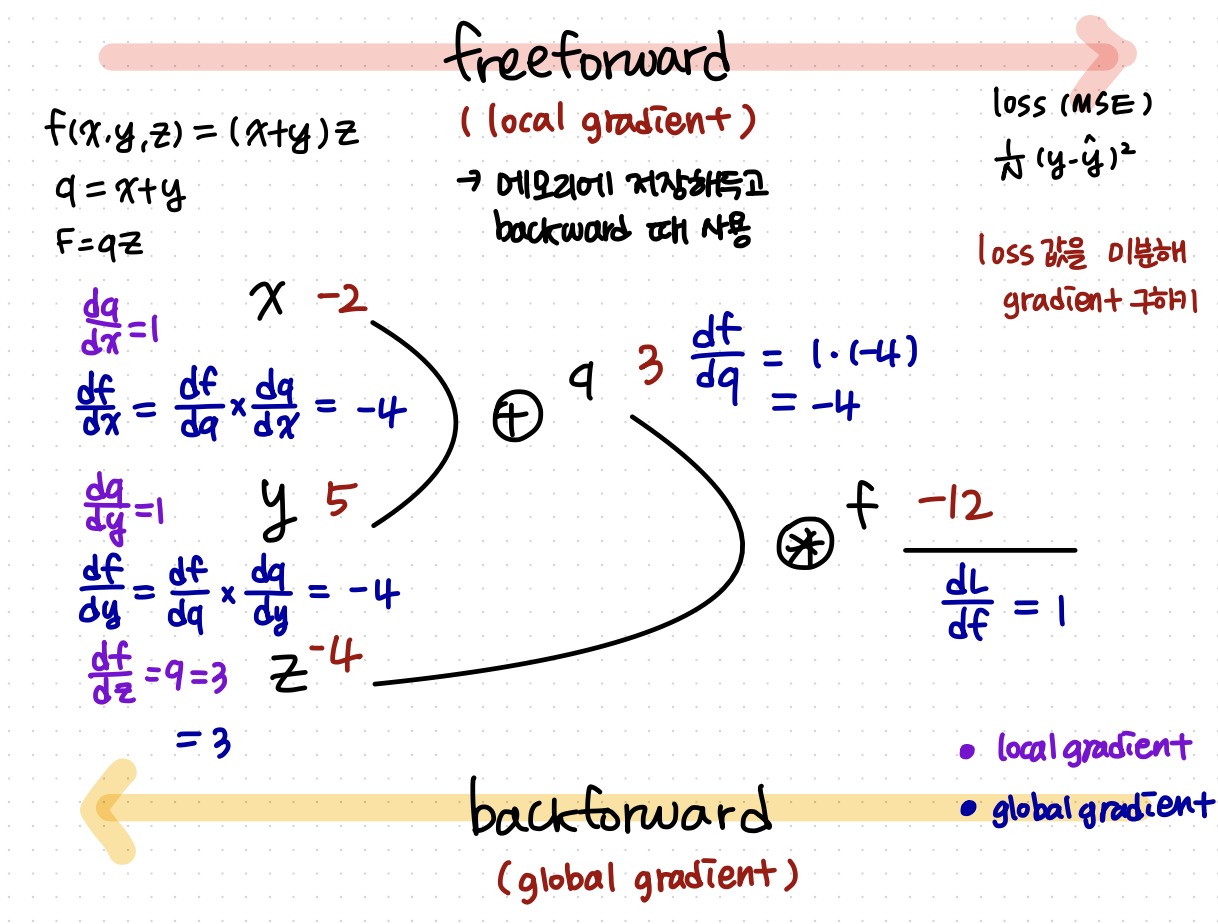
Simple example of backprop
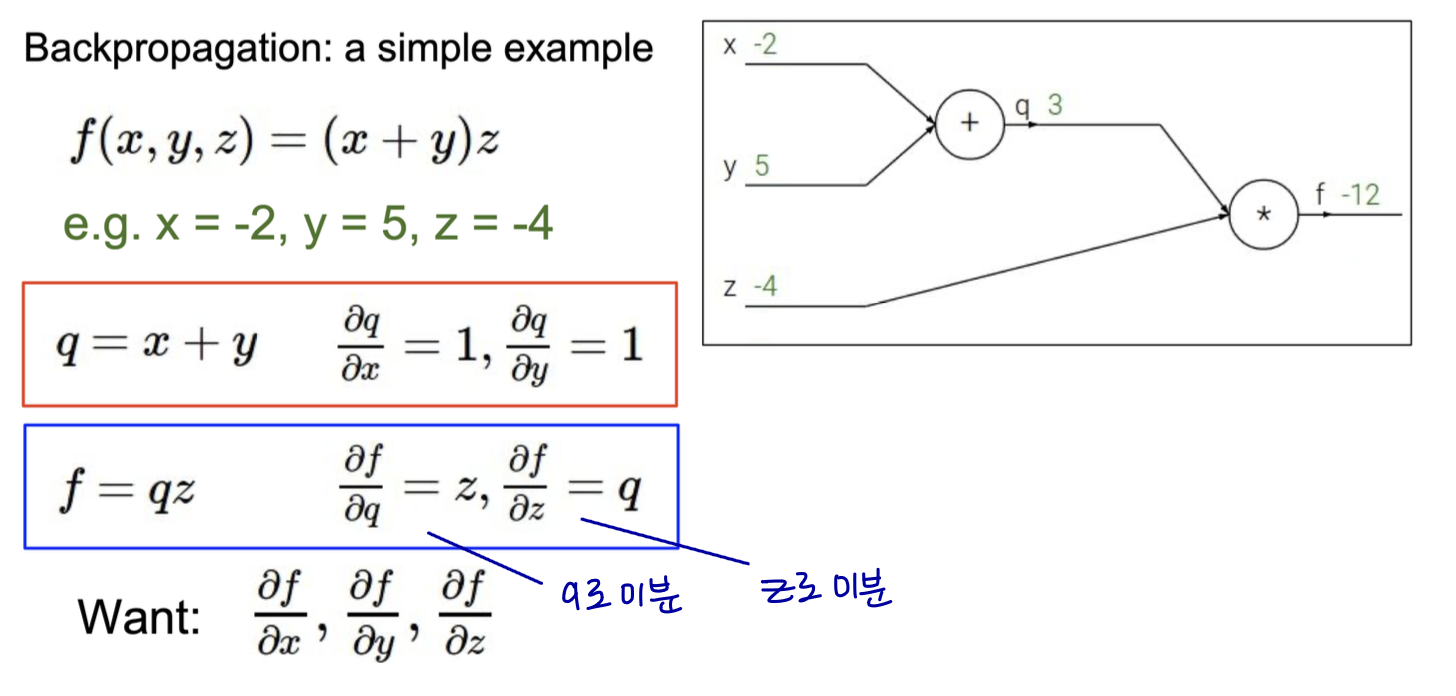
위의 예시를 backprop으로 푸는 방식은 다음과 같다.
Single-gate backprop
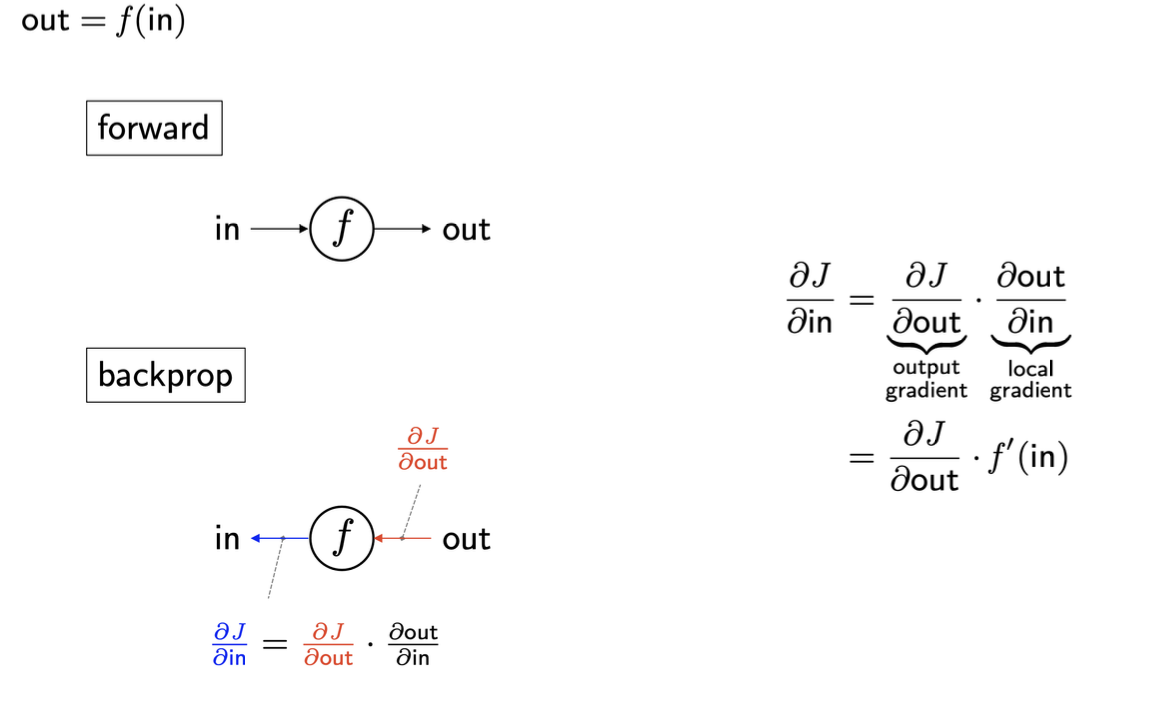
Sigmoid backprop
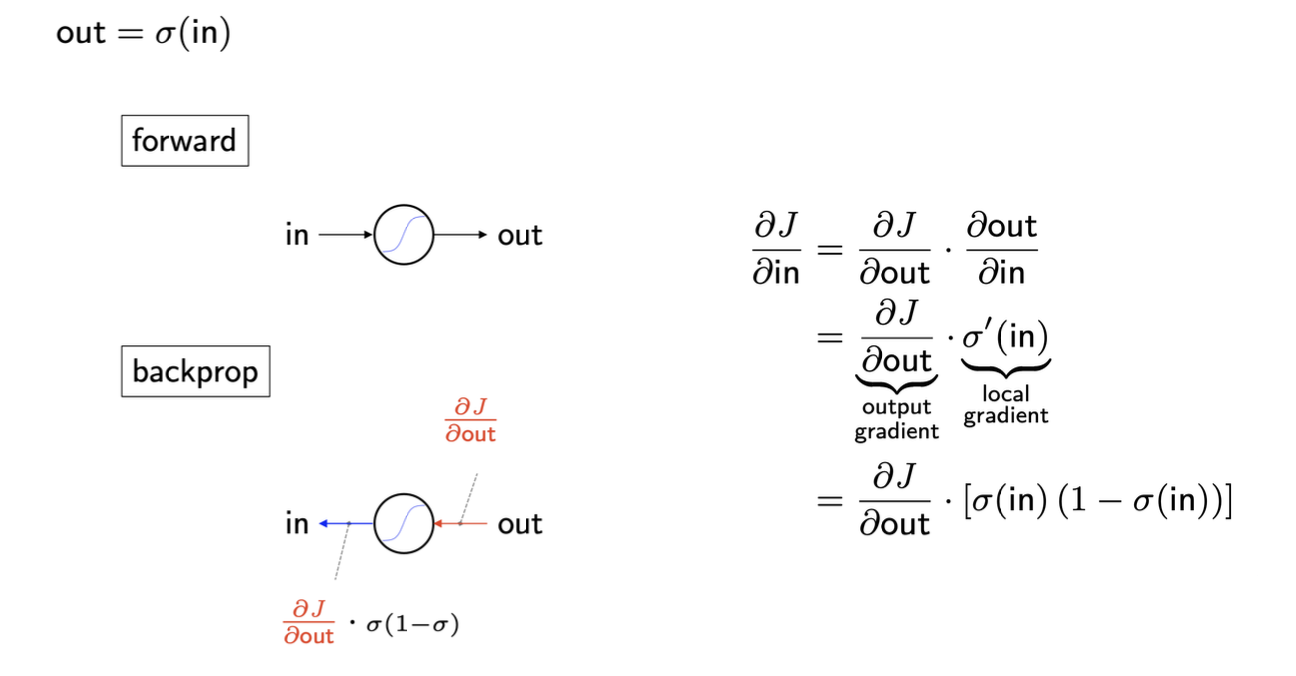
Multiplication backprop
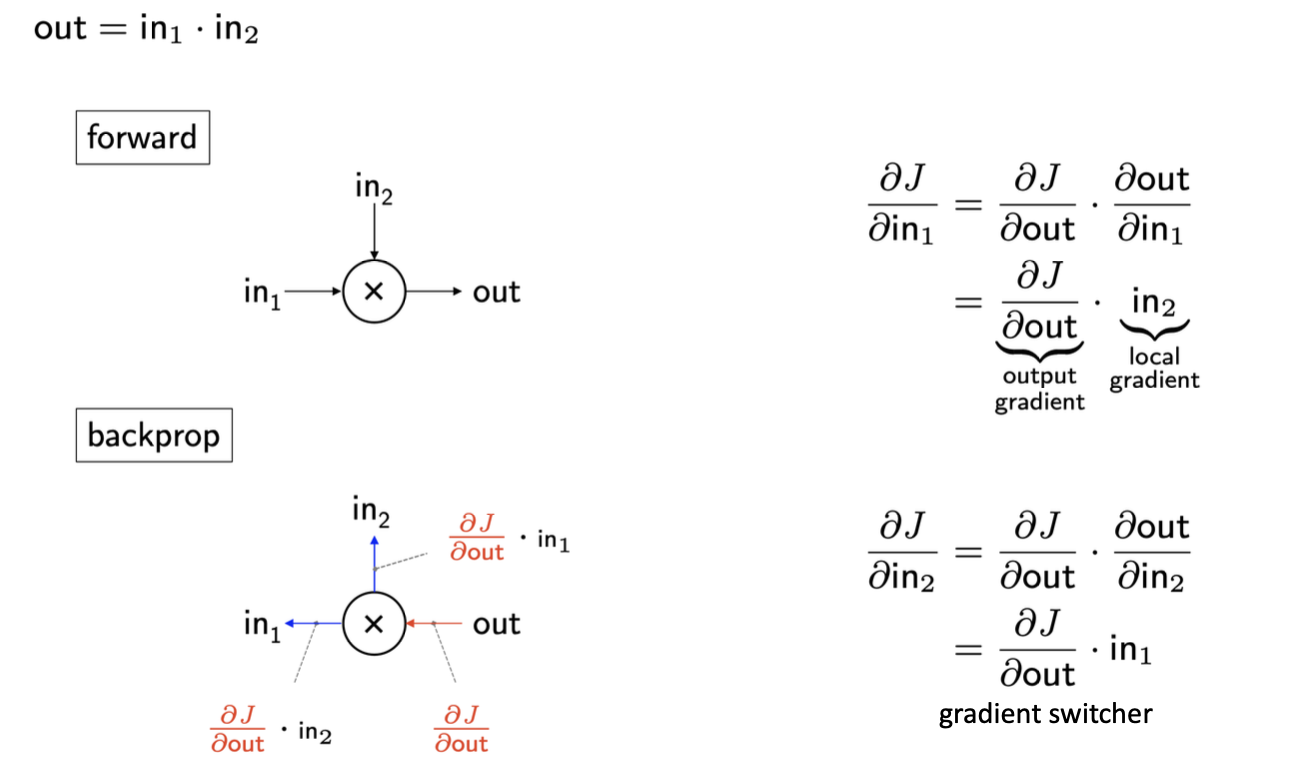
Summation backprop
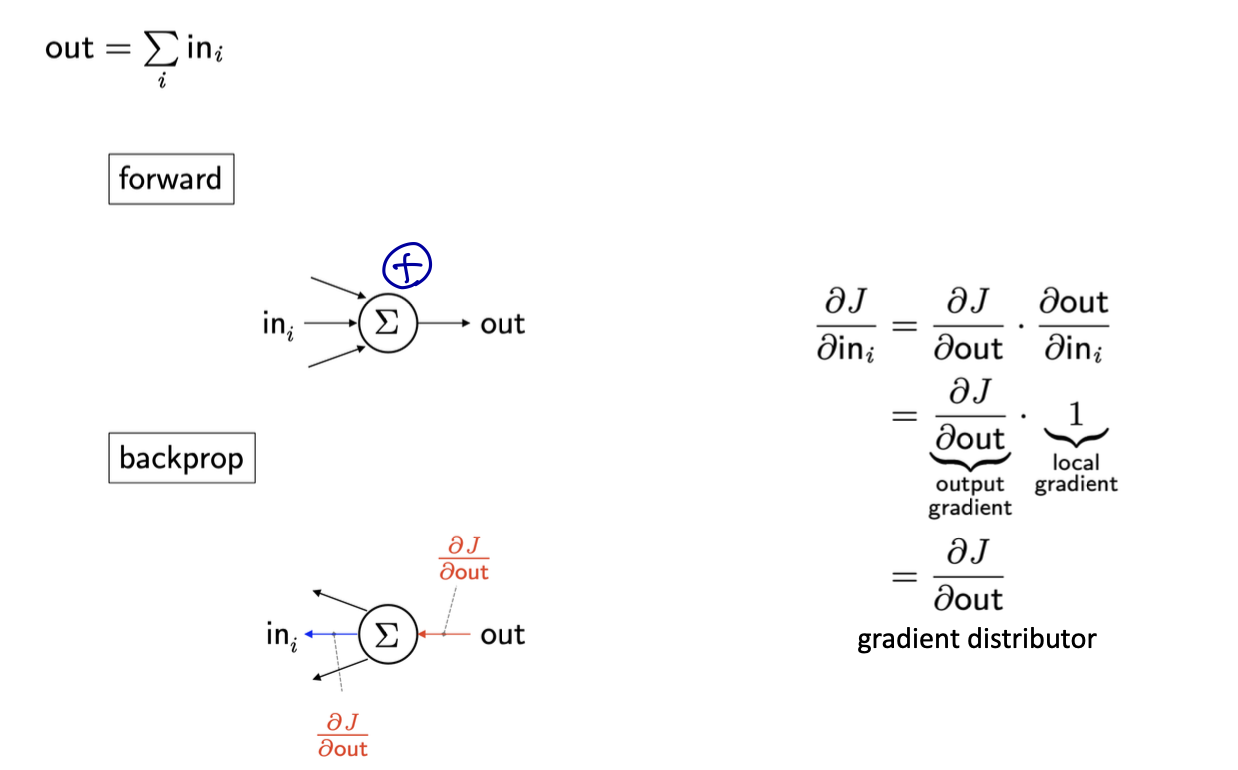
Max backprop
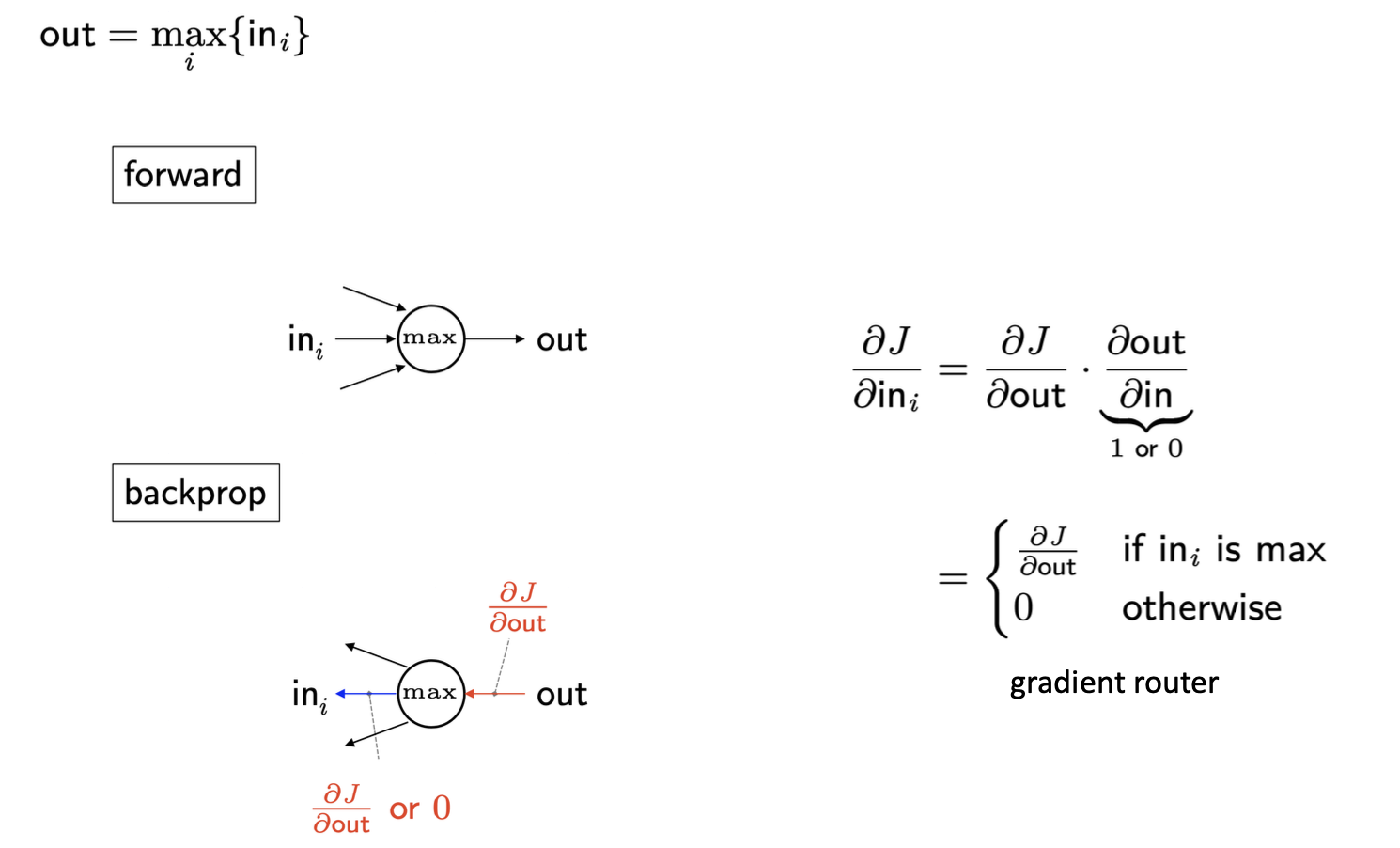
위의 공식을 이용하여 손으로 backpropagation을 풀어보면 다음과 같다.
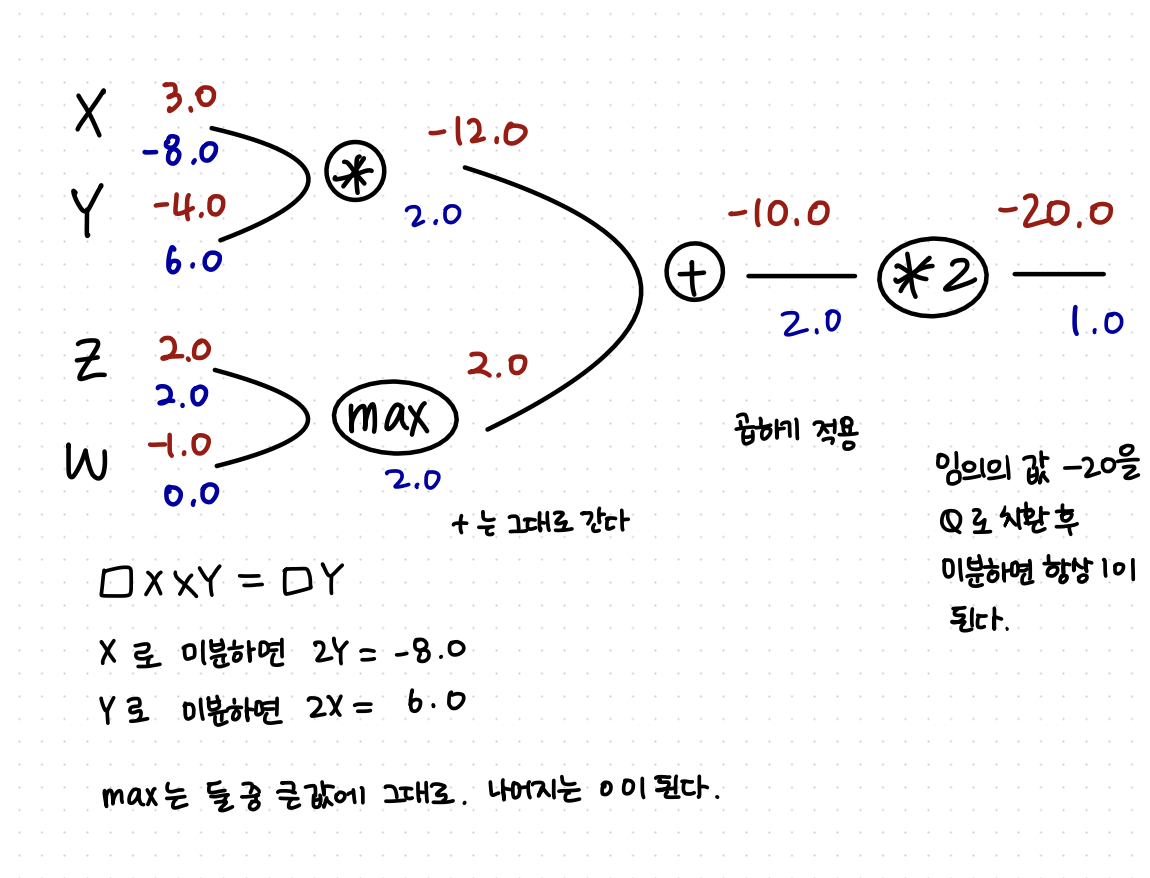
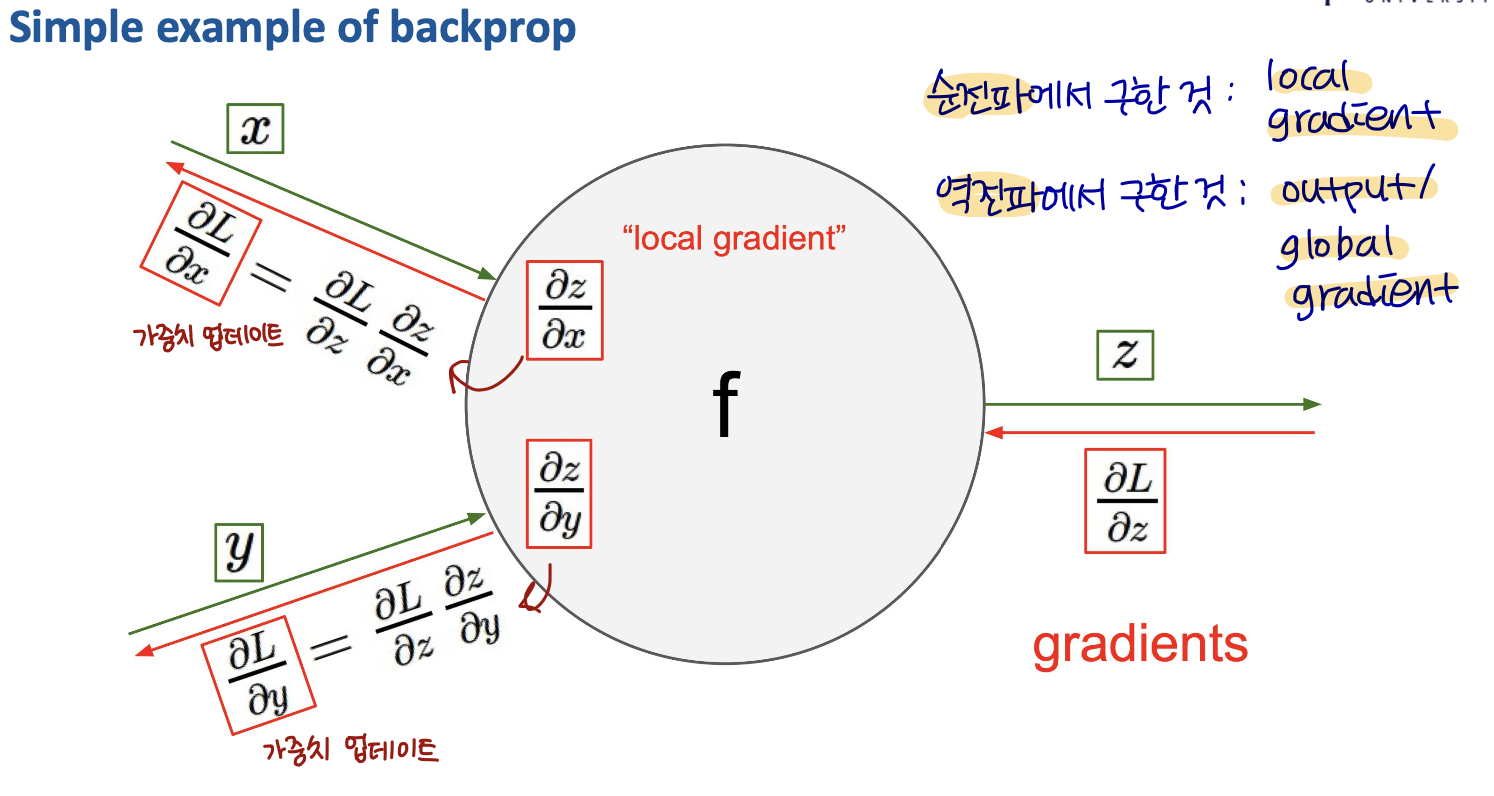
feedforward에서 구한 가중치 값 → local gradient
backprop에서 구한 가중치 값 → global gradient
이해가 쉽도록 직접 계산한 그림을 첨부했다