Attribute Set Closure
-
attribute α 의 집합이 주어졌을 때, F 아래 α를 함수적으로 결정되는 모든 attribute의 집합을 “closure of α under F” 라고 부른다.
-
주어진 애트리뷰트 집합에 의해 결정되는 모든 애트리뷰트의 집합
-
용도
- Super Key 테스트
- FD 테스트
- F+ 계산
-
α+를 계산하기 위한 알고리즘, the closure of α under F
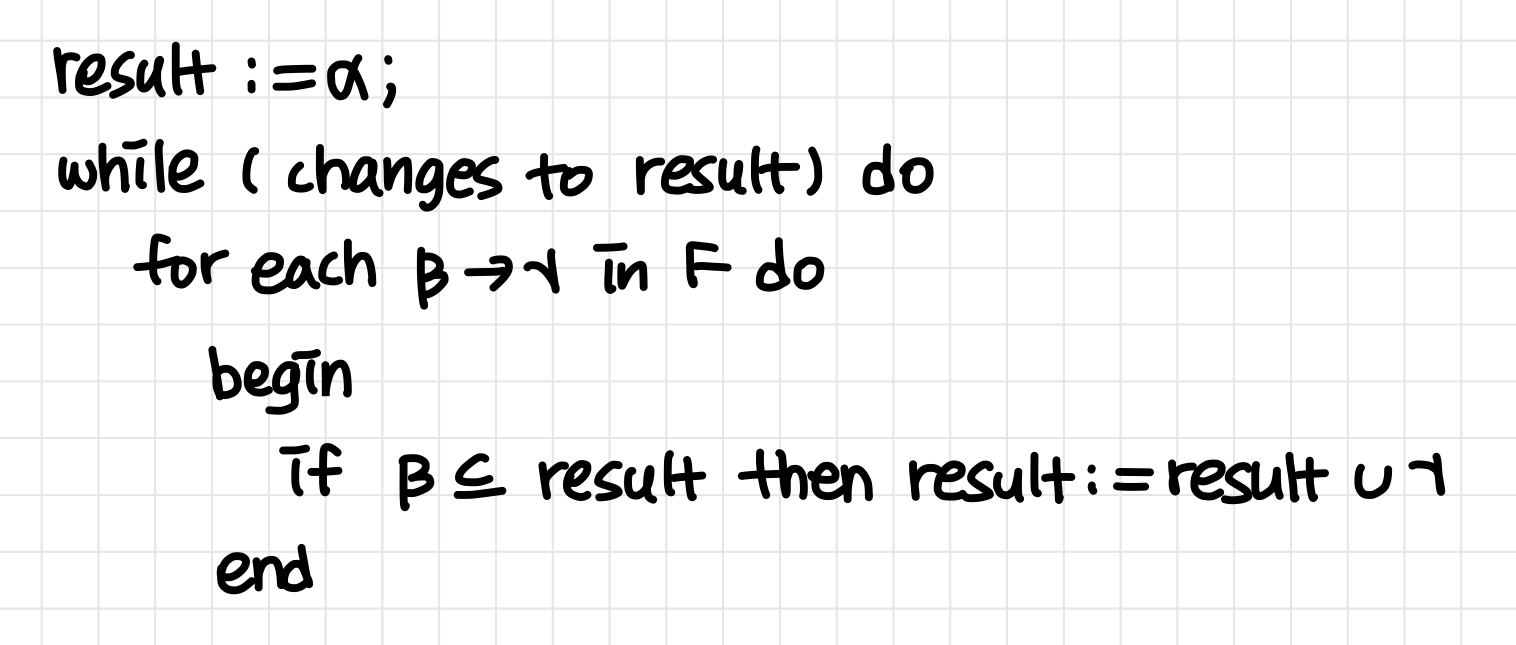
-
Uses of Attribute Closure
- attribute closure 알고리즘의 몇 가지 용도가 있다.
-
Super key 테스트
- α 가 super key인지 확인하기 위해 α+를 계산하고, α+가 R의 모든 attribute를 포함하는지 확인한다.
-
functional dependency 테스트
-
functional dependency α → β 가 성립하는지 확인하기 위해, β ⊆ α+ 인지 확인한다.
-
즉, attribute closure를 이용해 α+를 계산하고, α+가 β를 포함하는지 확인한다.
-
이것은 쉽고 값 싼 테스트이고 매우 유용하다.
-
-
F의 closure를 계산
-
각각의 S ⊆ γ+ 를 확인하기 위해, 각각의 γ ⊆ R 에 대해, γ+를 찾아낸다. 그리고 functional dependency γ → S를 도출한다.
-
e.g.) ABC → A, ABC → AB..
-
-
Example of Attribute Set Closure
attribute set closure는 해당 스키마의 candidate key를 찾아내기 위해 활용할 수 있다.
R = (A, B, C, G, H, I)
F = {A → B, A → C, CG → H, CG →I, B → H}
-
(AG)+
-
result = AG
-
result = AGB (A →B)
-
result = AGBC (A → C)
-
result = AGBCH (CG → H)
-
result = AGBCHI (CG →I)
-
result = AGBCHI (B → H)
-
-
AG는 candidate key 인가? YES
- AG는 super key 인가? YES
- Does AG → R? == Is (AG)+ ⊇ R YES
- Does G → R? == Is (G)+ ⊇ R NO
Covers
-
F’+ = F+ 인 임의의 F’를 F의 cover 라고 한다.
-
F와 동일한 Closure를 갖는 FD 집합
-
예) F {A → B, A → AC, A → BC} 와 F’ {A→B, A→C}
-
-
만약 {F - {g})+ = F+ or g ∈ (F - {g})+ 이면,
FD g ∈ F 는 불필요하다.
- 없어도 되는 FD
-
F’은 F의 중복이 없는 (minimal) cover이다.
-
F’+ = F+ 이고 F’는 불필요한 FD를 포함하지 않는다.
-
주어진 FD 집합과 동일한 최소의 FD 집합 (불필요한 FD 제거)
-
Canonical Cover
-
Functional dependency 집합은 다른 것들로 부터 유추가능한 불필요한 dependencies를 가지고 있을 수 있다.
-
e.g.) A → C 는 다음 집합에서 불필요하다. in: {A → B, B → C, A → C}
-
functional dependency의 일부분이 불필요할 수 있다.
-
α → β 에서 α는 LHS(Left Hand Side), β는 RHS(Right Hand Side)라고 부른다.
-
e.g. on LHS:
- F = {A → B, B → C, AC → D} 는 다음으로 간소화 될 수 있다. F’ = {A→ B, B → C, A → D}
- F = {A → B, B → C, AC → D} 는 다음으로 간소화 될 수 있다. F’ = {A→ B, B → C, A → D}
-
e.g. on RHS:
- F = {A → B, B → C, A → CD} 는 다음으로 간소화 될 수 있다. F’ = {A → B, B → C, A → D}
-
-
-
직관적으로, F의 canonical cover는 dependency 전체 혹은 일부에 불필요한 부분이 없는, F와 동일한 functional dependency 집합을 가지는 minimal 한 집합이다.
- F의 Extraneous Attributes를 모두 제와한 cover ⇒ canonical cover

Extraneous Attributes
-
Extraneous Attributes: 없어져도 무관한 애트리븉
-
정의: α → β in F.
-
만약 A ∈ α 이고,
F가 (F - {α → β}) U {(α - A) → β} 을 논리적으로 함축한다면
Attribute A는 α에서 무관하다.
-
만약 A ∈ β 이고,
(F - {α → β}) U {α → (β - A)} 가 F 임을 논리적으로 함축한다면
Attribute A는 β에 무관하다.
-
위의 각 경우에서 반대방향에서의 함축은 자명하다. stronger functional dependency는 항상 weaker one을 함축하기 때문이다.
-
F = A → B: strong
-
F’ = AC → B: weak
-
F → F’ 은 always trivial
-
but, F’ → F 는 don’t know
-
-
-
F = {A → C, AB → C} 를 가정해보자.
- AB → C에서 B는 무관하다. {A → C, AB → C} 이 A → C를 논리적으로 함축하고 있기 때문이다.
-
F = {A → C, AB → CD} 를 가정해보자.
- AB → CD에서 C는 무관하다. AB → CD는 C를 삭제하고 나서도 추론될 수 있기 때문이다.
Testing if an Attribute is Extraneous
-
functional dependency의 집합 F가 있고, F에 functional dependency α → β 가 있는 경우를 고려해보자.
-
α에서 어트리뷰트 A ∈ α 가 무관한지 테스트
-
F의 dependencies들을 이용해 ({α} - A)+를 계산한다.
-
({α} - A)+가 β를 포함하는지 확인한다. 만약 그렇다면, A는 α에서 무관한 애트리뷰트이다.
-
-
β에서 어트리뷰트 A ∈ β 가 무관한지 테스트
-
F’ = (F - {α → β}) U {α → (β - A)} 의 dependencies 만을 사용해 α+를 계산한다.
-
α+ 가 A를 포함하는 지 확인한다. 만약 그렇다면, A는 β에서 무관한 애트리뷰트이다.
-
Canonical Cover (cont.)
-
F의 canonical cover는 dependencies Fc의 집합이다. Fc such that
-
Fc+ = F+
-
Fc의 어떤 FD도 무관한 애트리뷰트를 포함하지 않는다.
-
Fc의 각 FD의 left side는 unique 하다.
-
-
즉, 정리하자면 Canonical cover란 불필요한 attribute는 없고, FD의 (동일한) 왼쪽 편이 두번 이상 나오지 않도록 한 cover이다.
Canonical Cover (cont.)
-
F의 Canonical cover 계산:
repeat
- F의 어떤 dependency를 대체하기 위해 union rule을 사용한다.
- α1 → β1 and α1 → β2 with α1 → β1β2
- α 또는 β가 무관한 애트리뷰트를 갖고 있는 functional dependency α → β 를 찾는다.
- 만약 무관한 어트리뷰트를 찾으면 α → β로 부터 그것을 지운다.
until F does not change
- F의 어떤 dependency를 대체하기 위해 union rule을 사용한다.
-
주의: 일부 무관한 어트리뷰트가 삭제된 후에 union rule이 적용될 수 있으므로 다시 적용해야 한다.
Example: Canonical Cover
-
R = (A, B, C), F = {A → BC, B → C, A → B, AB → C}
-
A → BC 와 A → B를 결합해 A → BC로 만든다.
- 집합은 이제 {A → BC, B → C, AB → C} 다.
-
AB → C에서 A는 무관하다.
- AB → C에서 A를 삭제한 결과가 다른 dependency들에 의해 논리적으로 함축될 수 있는지 확인한다.
- YES: 실제로, B → C가 이미 존재한다!
- 집합은 이제 {A → BC, B → C} 다.
- AB → C에서 A를 삭제한 결과가 다른 dependency들에 의해 논리적으로 함축될 수 있는지 확인한다.
-
A → BC 에서 C는 무관하다.
-
A → B와 다른 dependency들에 의해 A → C가 논리적으로 함축될 수 있는지 확인한다.
-
YES: A → B, B → C 에 transitivity를 이용한다.
- 더 복잡한 경우에서 A의 closure를 이용할 수 있다.
-
-
-
Canonical cover is: {A → B, B → C}
보완할 부분이 있으면 댓글 남겨주세요. :)
