Likelihood

Rewind

• Task

  • Classification(분류): binary / multiclass / multilabel

  • Regression(회기): scalar / vector

• Data

  • N-point data set D = {(x1, y1), (x2,y2), … , (xn, yn)}

  • unknown 데이터분포 P data(Θ)에 의해 생성됨

• Model

  • Neural Network (신경망)

  • y^ = fΘ(x) / p(y| x; Θ)

  • 모델 아키텍쳐

• Training

  • 모델 파라미터 Θ 추정

  • Cost / Loss function (비용/손실 함수)

  • 비용 함수를 최소화하는 Θ 찾기 → 최적화 (Gradient Descent: 경사하강법)

  • 신경망에서 자명하지 않은 gradient 계산 → Backpropagation (역전파)

• Evaluation

  • Training / Validation / Test data

  • K-fold validation

Probabilistic Model

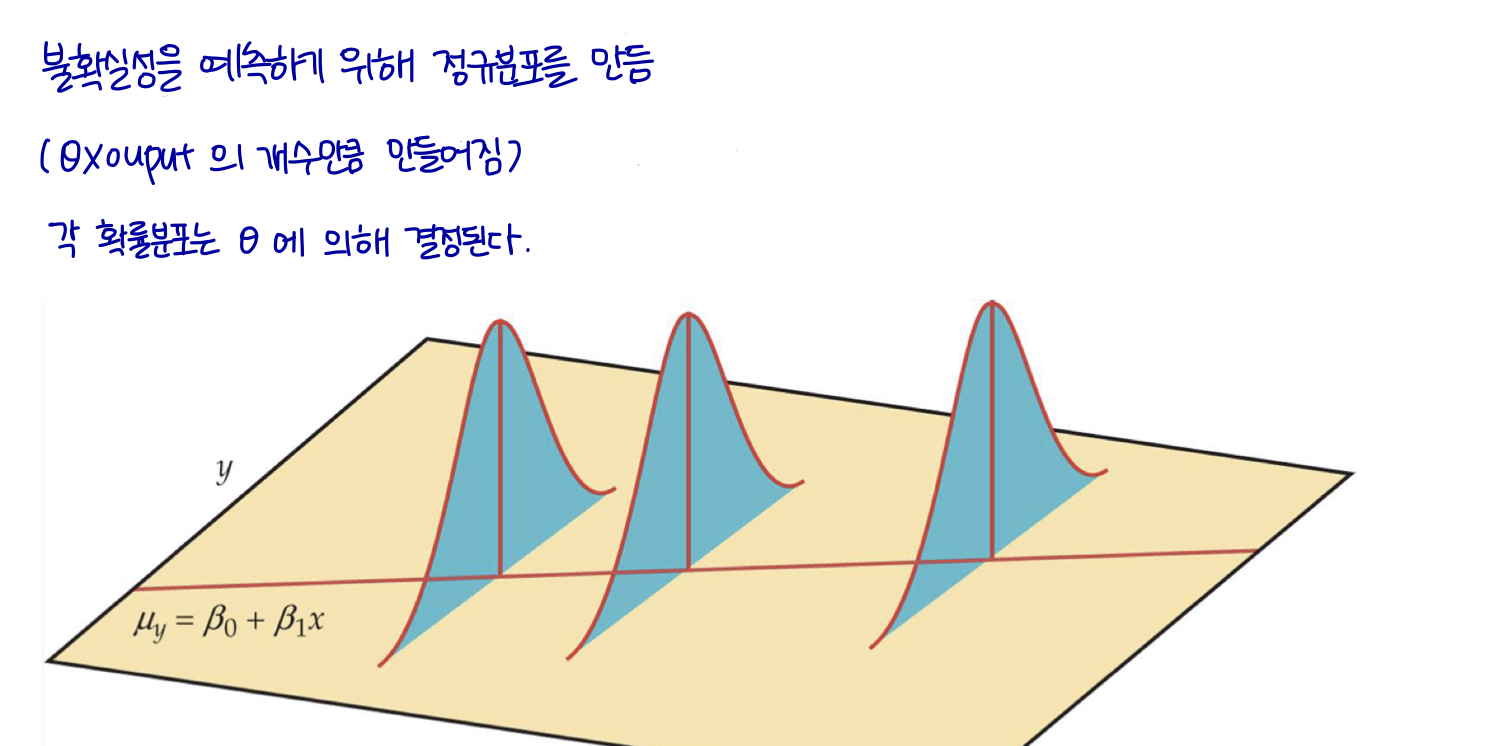
• 불확실성 → 어떻게 모델에 반영 → 정규 분포

• 주어진 입력에 대해 정확한 출력을 완벽하게 예측할 수 없다.

  • input-output mapping 에 대한 지식 부족 (모델 불확실성)

  • 매핑의 내재적 확률 (데이터 불확실성)

• 다음의 조건부 확률 분포를 사용하여 불확실성을 포착할 수 있다.

  • e.g.) classification p(y=c | x; Θ) = f(x; Θ); f가 아핀 함수이면 → logistic regression

  • e.g.) regression

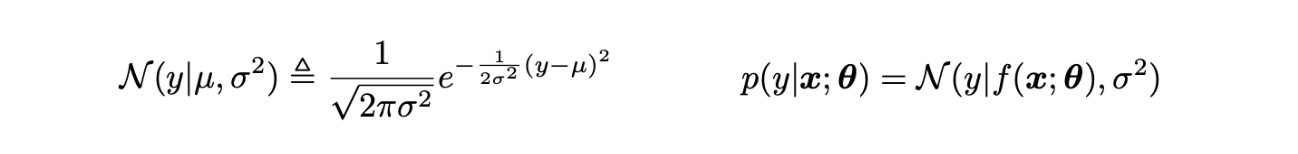
Maximum Likelihood Estimation

최대 우도 함수 추정

• Toy example

  • 어떤 분포가 데이터를 생성할 가능성이 가장 높은가?

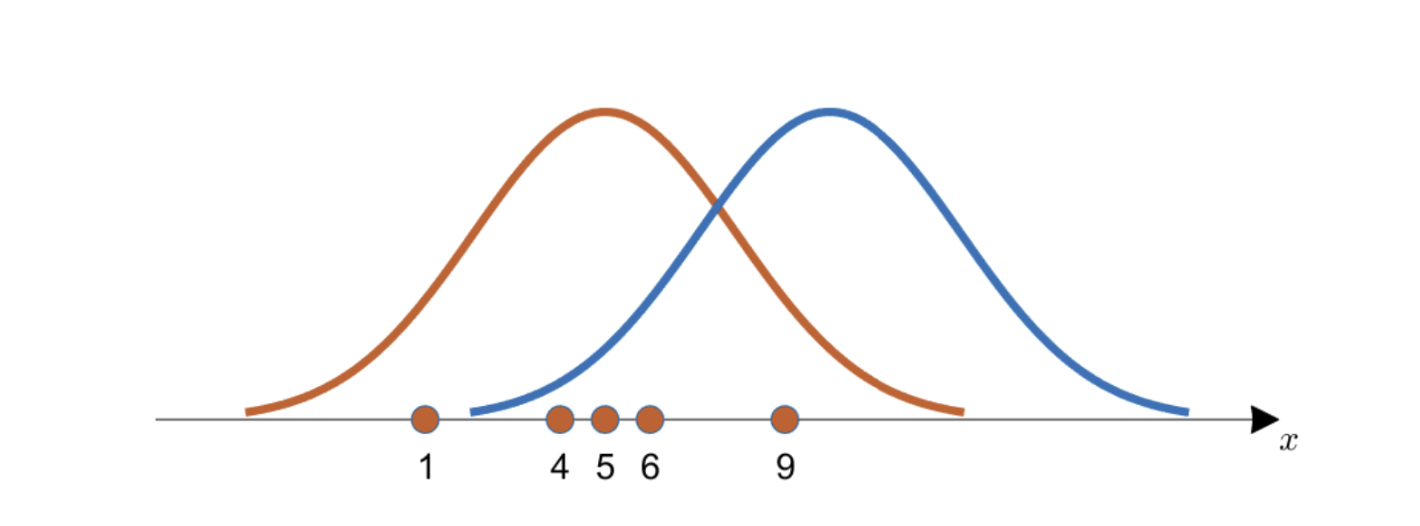
Maximum Likelihood Estimation (cont.)

일부 관찰된 데이터가 주어졌을 때 가정된 확률분포의 매개변수를 추정하는 방법

Maximum Likelihood Estimation (cont.)

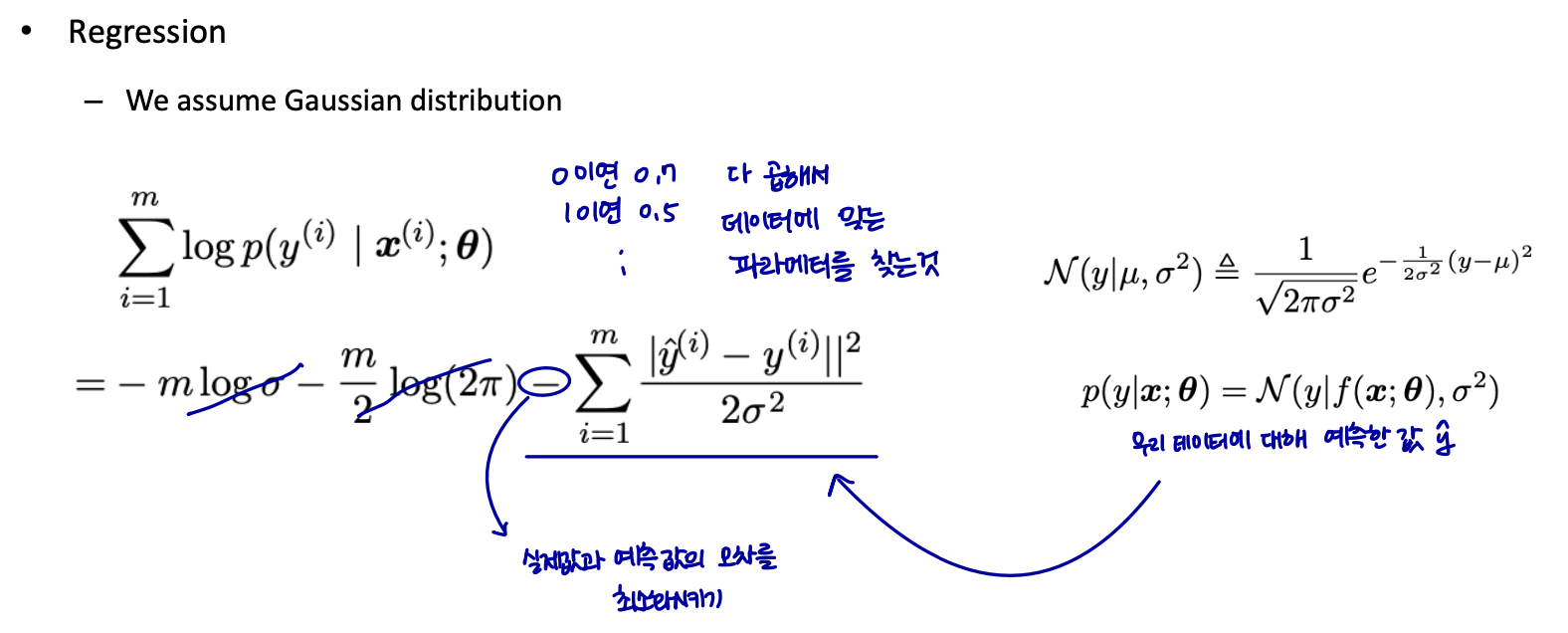
Maximum Likelihood Estimation (cont.)

• Binary Classification (이진 분류)

  • 베르누이 분포를 가정한다.

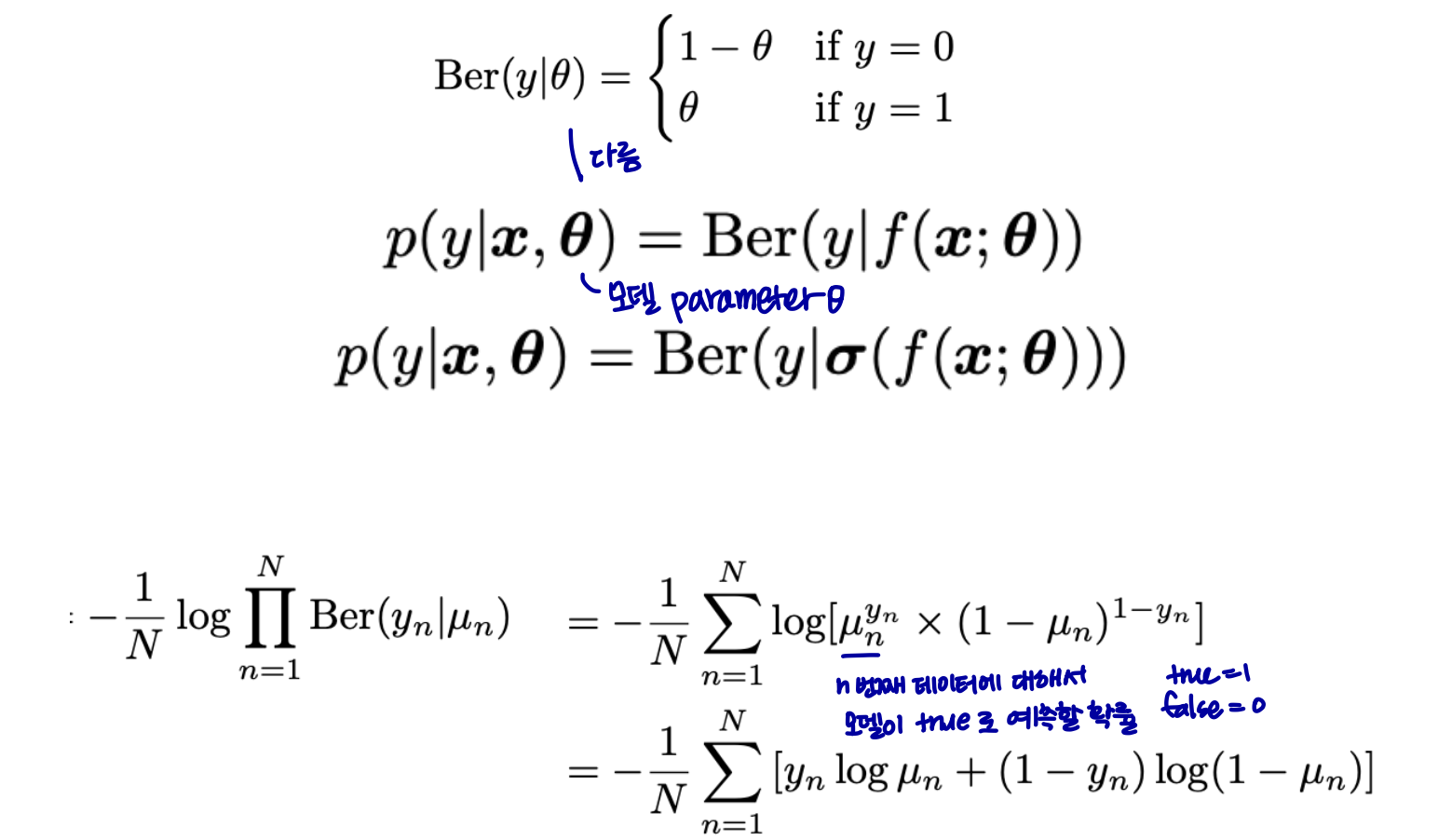
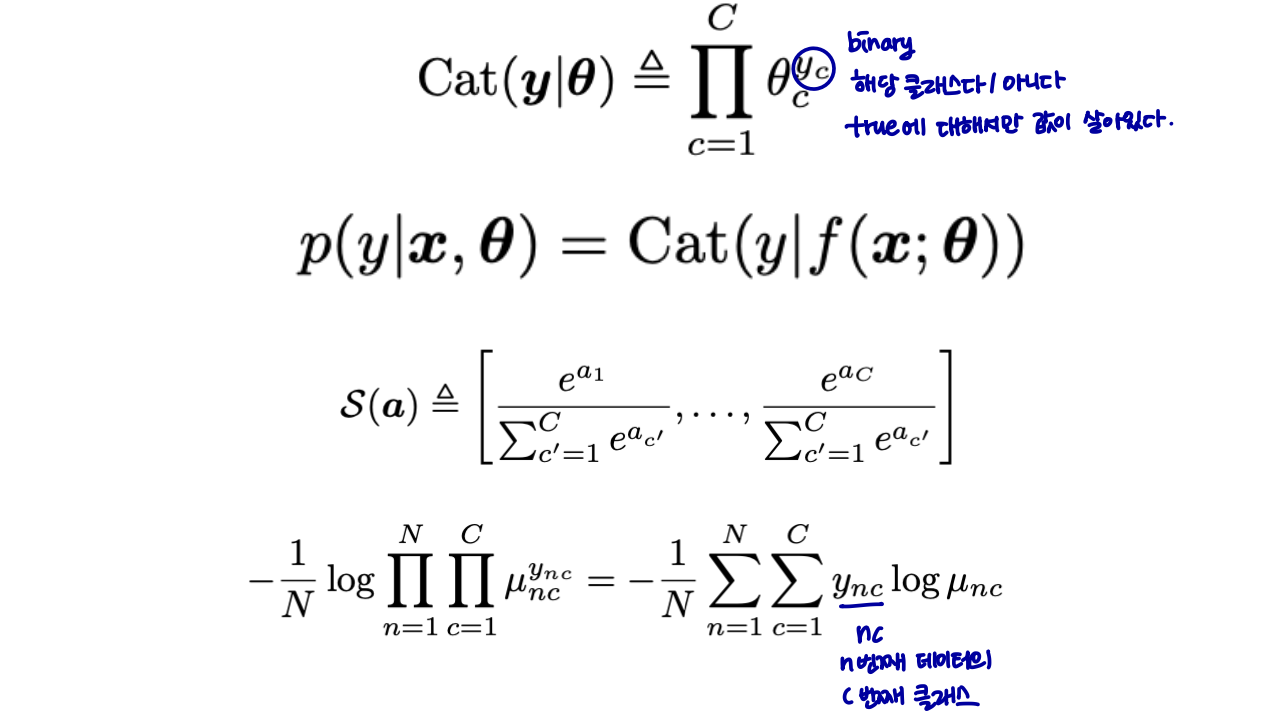
• Multi-class classification (다중 분류)

  • 범주형(=멀티누이) 분포를 가정한다.

Evaluation

• Training set: 모델 파라미터 추정 (경사하강법, 역전파 알고리즘)

• Validation set: 모델 선택

• Test set: 최종 검증

  • 제일 좋은 모델로 성능 검증 → k-fold transfication 방식

k-fold 쓰는 이유

일반적으로 머신러닝 모델을 학습시키기 위해서 데이터를 훈련 데이터, 검증 데이터, 테스트 데이터로 나눈다. k-fold는 데이터를 k개의 서로 다른 부분집합으로 나누어, 각각의 부분집합을 순차적으로 검증 데이터로 사용하고 나머지 부분집합을 합쳐서 훈련 데이터로 사용하는 방법이다. 이렇게 k번 반복하여 모델을 학습하고 평가한 후, k개의 성능 지표의 평균을 계산하여 최종 성능을 평가한다.

k-fold 교차 검증을 사용하면, 모델의 일반화 성능을 높일 수 있다. 또한 모델 성능을 평가할 때, 특정 데이터에 대한 과적합을 방지할 수 있다. k-fold 교차 검증은 데이터의 크기가 작을 때 특히 유용하며 머신러닝 모델의 하이퍼파라미터 튜닝에도 사용된다.

Appendix: Properties of the PDF

어떤 단일 값 a에 대해, 다음 수식이 성립한다.

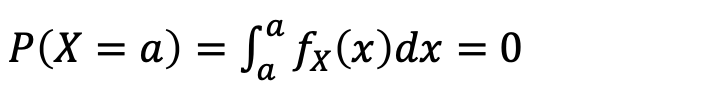
Appendix: Properties of the PDF (cont.)

Appendix: Simple Linear regression model

Appendix: Likelihood?

• 주사위 두 개가 있다

  • 우리가 알고 있는 일반적인 주사위 A

  • 무언가 조작이 가해져서 3이 나올 확률이 0.5이고 나머지가 uniform한 주사위 B

X1 : A → 결과값이 랜덤하게 나왔으므로 주사위 B보다는 A을 던졌을 확률이 더 높다.

X2 : B → 3이 나올 확률이 높은 주사위 B를 던졌기 때문에 결과값에 3이 많이 나온 것이다.

Appendix: Likelihood

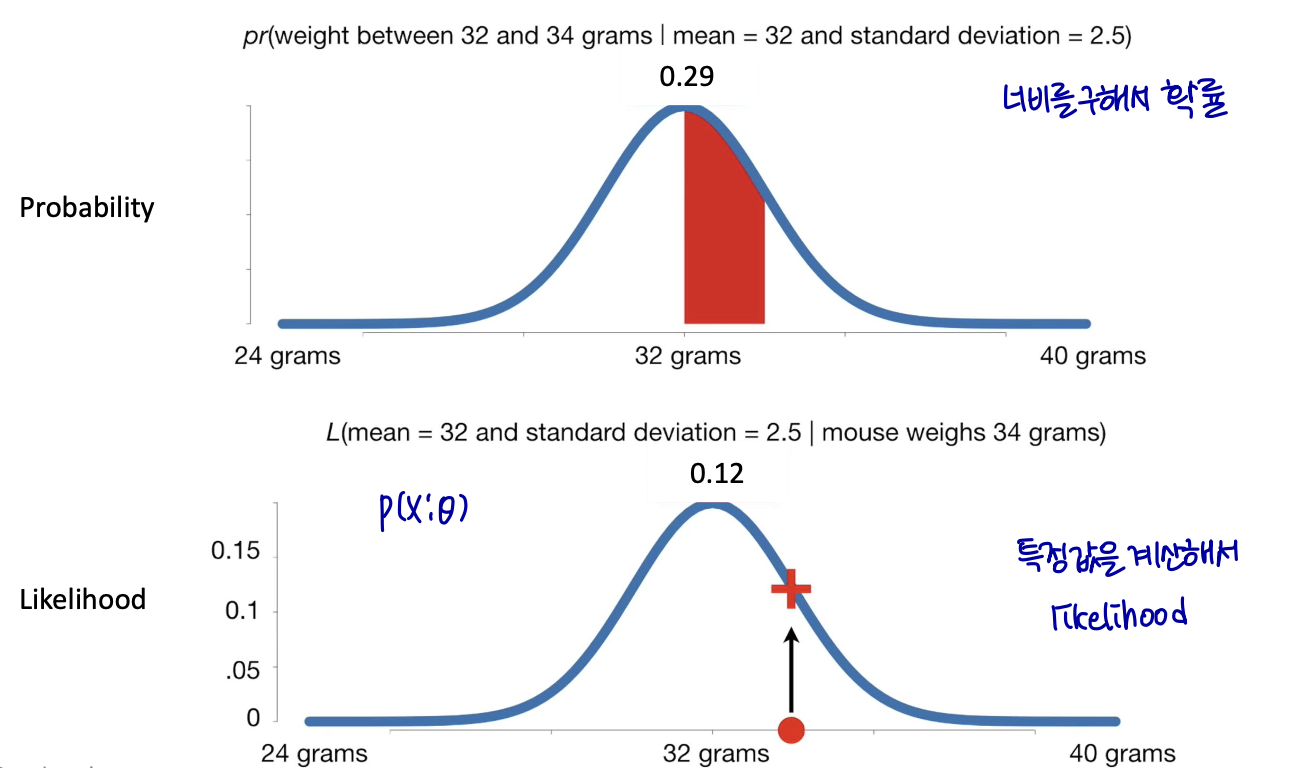
• PDF는 probability가 아니고, single value에 대한 probability는 항상 0이다.

• PDF를 사용하면 data가 A, B 분포에서 왔을 가능성을 측정해서 더 가능성이 큰 분포를 선택할 수 있다.
  (*PDF: Probability distribution function, 확률밀도함수)

우도 함수는 선택한 통계 모델의 매개변수 함수로 표시되는 관찰 데이터의 공동 확률이다.

통계 모델은 샘플 데이터 생성에 관한 일련의 통계적 가정을 구현하는 수학적 모델이다.

Appendix: Likelihood (cont.)

• L(Θ | x)로 표기. data가 관측되었을 때 해당 parameter에서 나왔을 가능성

• 이산확률 분포

  

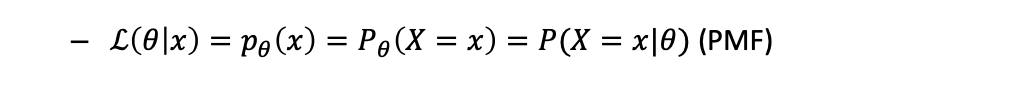
• 연속적인 확률 분포

  

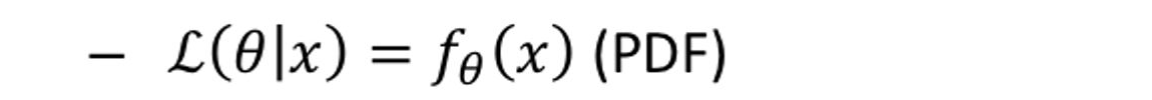
Appendix: Likelihood (cont.)

Appendix: Maximum Likelihood Estimation

• 관찰 데이터가 주어지고 distribution or model은 알고 있고 parameter를 모른다고 가정하자.

  • data 로부터 parameter를 알고 싶은데 어떻게하나?

    • parameter 별로 likelihood를 계산해서 likelihood가 최대로 되는 parameter를 선택

  • parameter는 사실 discrete 하지 않고 continuous인데?

    • log likelihood를 사용하면 된다. 로그 함수는 연속 함수이기 때문에, 로그 우도 함수는 파라미터 공간에서 매끄러운 함수로 만들어준다. 이는 파라미터 공간에서 최적화 알고리즘이 빠르게 수렴할 수 있도록 도와준다.

• 결합 우도를 최대화하는 Θ 찾기

  • L(Θ|x) = p(x1, … , xn; Θ)

• Θ = argmax L(Θ|x)

  • 가능한 모든 parameter 중에 주어진 data에 대한 likelihood를 maximize하는 parameter를 선택

• 보통 log likelihood를 사용한다.