최적화

Optimization

가장 간단한 경우, 최적화 문제는 허용된 집합 내에서 입력 값을 체계적으로 선택하고 함수의 값을 계산하여 실제 함수를 최대화하거나 최소화하는 것으로 구성된다.

최적화는 심층 신경망에서 중요하고 어렵고 비용이 많이 드는 부분이다.

비용 함수를 대폭 감소시키는 신경망의 파라미터 Θ 찾기, J(Θ)

Preliminaries

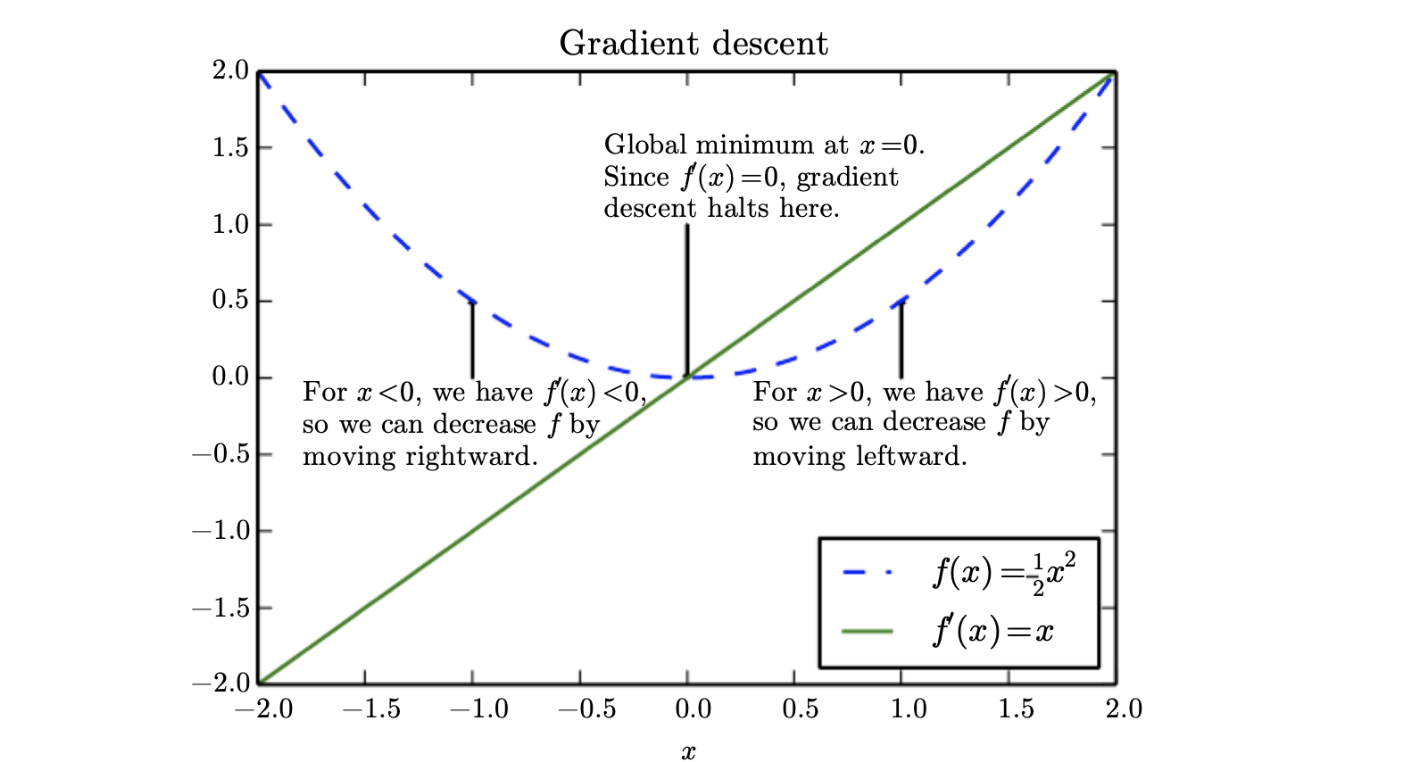
제 1도 함수 (gradient)

• Slope
• Jacobian matrix

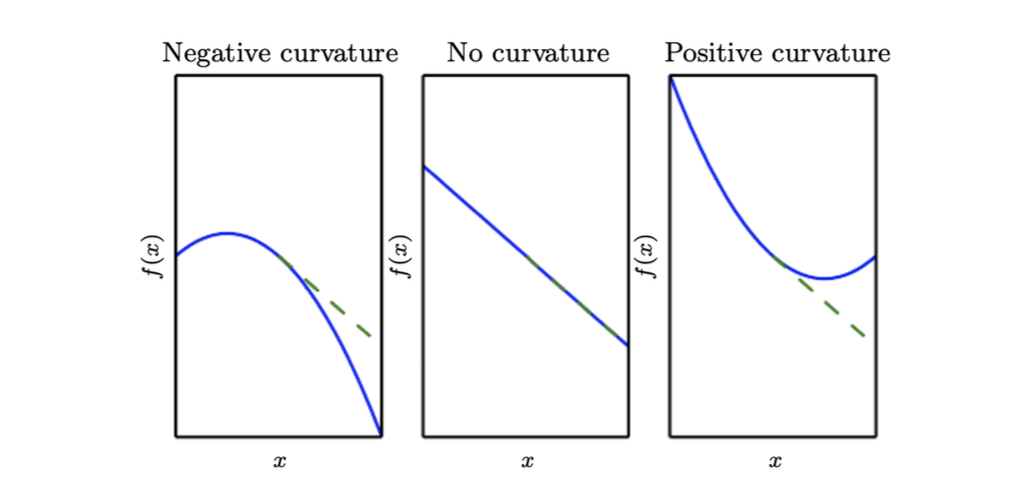
제 2도 함수

• Curvature
• Hessian matrix

• f’(x) = 0 → 임계점 or 정류점

  • 파생 모델은 어느 방향으로 이동해야 하는지에 대한 정보를 제공하지 않는다.

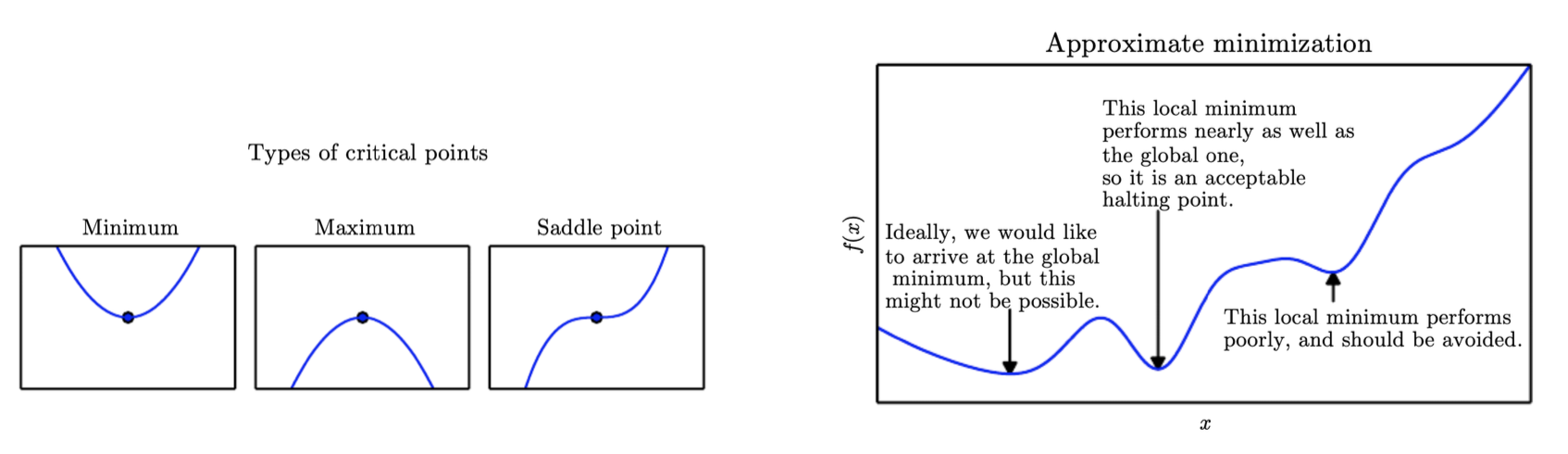
  • Local miminum / Local maximum / Saddle points

  • 고차원에서는 saddle point가 local minimum보다 훨씬 더 일반적이다.

Differences from pure optimization

대부분의 기계 학습 알고리즘의 목표는 테스트(unseen data)와 관련하여 정의된 성능 측정을 개선하는 것이다.

• intractable (다루기 힘든 경우)

• 간접적으로 최소화 (training data 이용)

J(Θ) 줄이기 → 그렇게하면 test set의 성능이 향상될 것으로 기대한다.

• 순수 최적화의 목표는 J를 최소화하는 것이다.

(*J(Θ): 비용 함수)

전형적인 비용함수

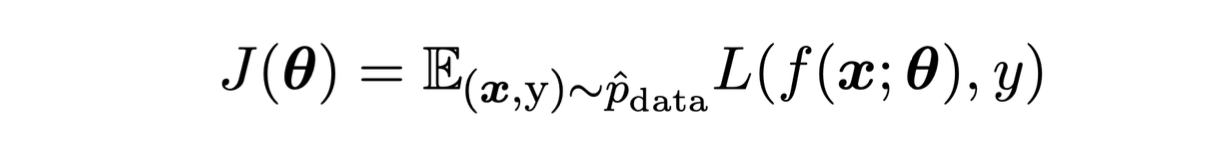
Empirical Risk Minimization

ML 알고리즘의 목표는 예상되는 일반화 오류를 줄이는 것이다.

• This quantity is known as the risk.

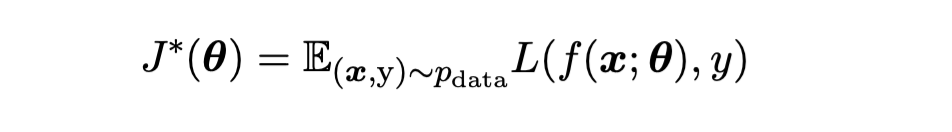
대부분의 경우, 우리는 데이터 분포를 알지 못하고 훈련 데이터 셋만 가지고 있다.

ML 문제를 최적화 문제로 변환

• training set 에서 예상되는 손실 최소화 → 위험 감소

• 과적합 이슈

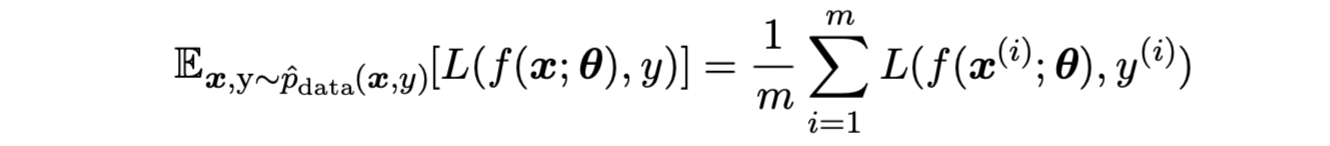
Surrogate Loss Functions and Early Stopping

손실함수 (e.g.) classification 오류)를 효율적으로 최적화할 수 없는 경우가 있다.

• e.g) 0-1 손실은 일반적으로 다루기 어렵다.

대신, 우리는 대리 손실 함수를 최적화한다.

• 프록시(proxy) 역할 수행

• e.g.) 올바른 클래스의 negative log-likelihood는 일반적으로 0-1 손실에 대한 대리로 사용된다.

조기 정지

• ML에서 훈련 알고리즘은 일반적으로 local minimum에서 중단되지 않는다.

• 일반적인 중지 기준은 실제 기본 손실함수를 기반으로 한다.

  • validation set

Additional

Surrogate loss function (대리 손실 함수):

• Loss function이 학습하기 적절하지 못하면 (ex 0-1 loss, why? → 미분이 불가능 해서 gradient(기울기) 구할 수 없음 → 그럼 무엇이 문제? Gradient descent를 사용하기가 어려워서 모델을 최적화 시키가 어려움)

• Classification 문제에서 Cross entropy를 사용하는게 예시

Minibatch stochastic methods

딥 러닝 및 기계 학습에서 일반적으로 사용되는 방법.

• 간단히 확률적 방법이라고 부른다.

미니 배치 크기와 관련된 요인

• 배치가 클수록 기울기를 더 정확하게 추정할 수 있다.

• GPUS를 사용할 때는 배치 크기가 2인 전력이 더 나은 런타임을 제공하는 것이 일반적이다.

• 작은 배치는 노이즈로 인해 정규화 효과를 제공할 수 있다.

Stochastic Gradient Descent: 확률적 경사하강법

SGD와 그 변형은 아마도 일반적으로 기계 학습, 특히 딥 러닝에 가장 많이 사용되는 최적화 알고리즘일 것이다.

m 개 샘플의 미니 배치에서 평균 기울기(gradient)를 취함으로써 기울기의 편향되지 않은 추정치를 얻을 수 있다.

SGD 알고리즘의 중요한 매개 변수는 학습률(learning rate)이다.

• 학습률은 시행착오를 통해 선택할 수 있지만, 일반적으로 목표 함수를 시간 함수로 플롯하는 학습 곡선을 모니터링하여 선택하는 것이 가장 좋다.

• 이것은 과학이라기보다는 예술에 가까우며, 이 주제에 대한 대부분의 지침은 다소 회의적으로 여겨져야 한다.

SGD gradient가 최솟값(minimum)에 도착했음에도 사라지지 않는다.

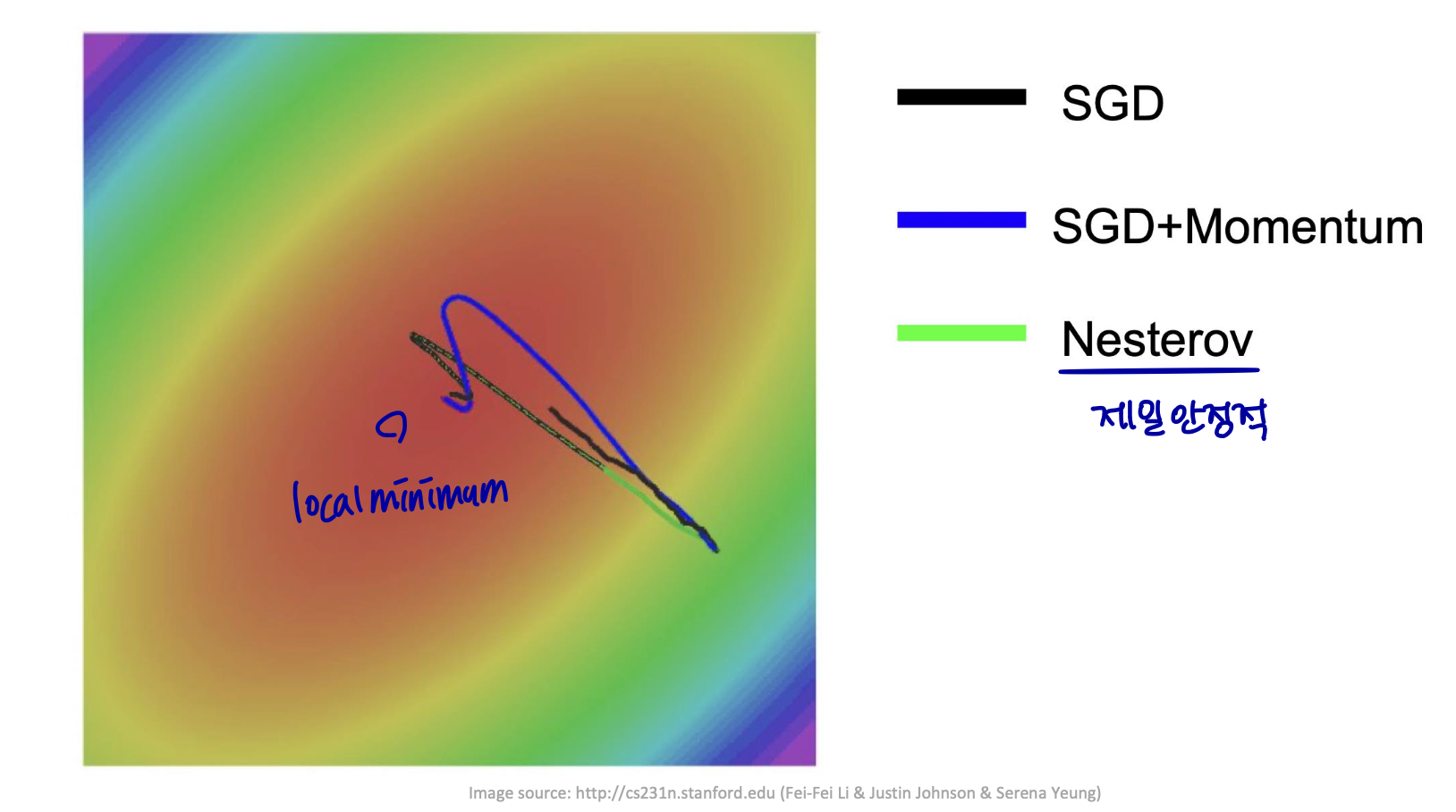
→ SGD(Stochastic Gradient Descent)는 볼록 함수의 경우 최솟값에 도착하면 수렴한다. 그러나, 비볼록 함수의 경우,처음 시작점(보통 딥러닝에서는 처음 시작점은 무작위로 주어짐)이 global minimum 보다 local minimum에 더 가까운 경우, 경사하강법에서 local minimum에 도달하면, f'(x)=0이 되어 더이상의 업데이트가 진행되지 않는다.

이러한 문제를 해결하기 위해서는, SGD 대신 더 나은 최적화 알고리즘을 사용하거나, SGD에 일부 변형을 가한 알고리즘을 사용하면 된다.

예를 들어, 모멘텀(Momentum)이나 AdaGrad, RMSProp, Adam 등의 최적화 알고리즘이 SGD보다 지역 최솟값에 빠질 확률이 적고, 더 빠르게 전역 최솟값(global minimum)에 도달할 수 있다.

• 시간이 지남에 따라 점진적으로 학습률을 낮추는 것이 필요하다.

• c.f. 총 비용 함수의 실제 기울기가 작아지고 배치 기울기 하강을 사용할 때 0이 된다.

업데이트당 계산 시간은 training example 수에 따라 증가하지 않는다.

SGD는 다음 조건에서 문제가 발생할 수 있다.

• Local minimum / Saddle point

• Gradient noise

• Poor condition

Momentum

경사하강법을 시행할 때, 학습률이 너무 작은 경우, 극솟값에 다다르는 속도가 너무 느리게 되어 많은 학습이 필요하다.

또한 처음 시작점(보통 딥러닝에서는 처음 시작점은 무작위로 주어짐)이 global minimum 보다 local minimum에 더 가까운 경우, 경사하강법에서 local minimum에 도달하면, f'(x)=0이 되어 더이상의 업데이트가 진행되지 않는다.

이러한 한계점을 해결하기 위해 모멘텀이 나왔다.

볼링공이 매끈한 표면의 완만한 경사를 따라 굴러간다고 하자. 볼링공은 처음에는 느리게 출발하지만, 종단속도에 도달할 때까지는 빠르게 가속될 것이다. 이것이 보리스 폴랴크가 1964년에 제안한 Momentum 최적화의 간단한 원리이다.

반대로 표준적인 경사하강법은 경사면을 따라, 일정한 크기의 스텝으로 조금씩 내려가기 때문에, 모멘텀에 비해, 맨아래에 도착하는데 시작이 더 오래 걸릴 것이다.

모멘텀의 방법은 학습을 가속화하도록 설계되었다.

• SGD는 매우 인기있지만 가끔 느리다.

• 높은 곡률 / 작지만 일정한 gradient / noisy gradients

이전 그레이디언트의 기하급수적으로 감소하는 이동 평균을 누적하고 해당 방향으로 계속 이동한다.

• 이는 두 가지 문제를 해결한다.

  • 상태 불량

  • SGD의 분산

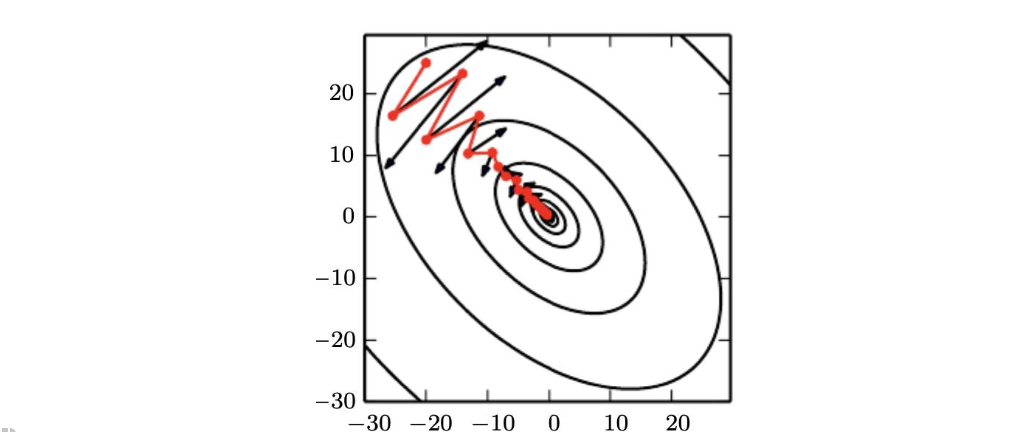
Momentum (cont.)

• Momentum

  • 물리학 (질량*속도)에서 파생된다.

  • 속도 v: 파라미터가 공간을 통과하는 방향 및 속도

    • 음의 기울기(gradient)의 지수적 감소 평균

  • 마찰 a: 이전 그레디언트의 기여도가 기하급수적으로 감소하는 속도를 결정한다.

    • 𝛼가 𝜖에 상대적으로 클수록 이전 그레이디언트가 현재 방향에 영향을 준다.

  • 실제로 사용되는 일반적인 𝛼 값에는 0.5, 0.9 및 0.99가 포함된다.

Momentum 최적화는 이전 gradient가 얼마였는지를 상당히 중요하게 생각한다. 따라서 매 반복에서 현재 graident를 (학습률 a를 곱한 후) 모멘텀 벡터 m에 더하고, 이 값을 빼는 방식으로 가중치를 업데이트 한다.

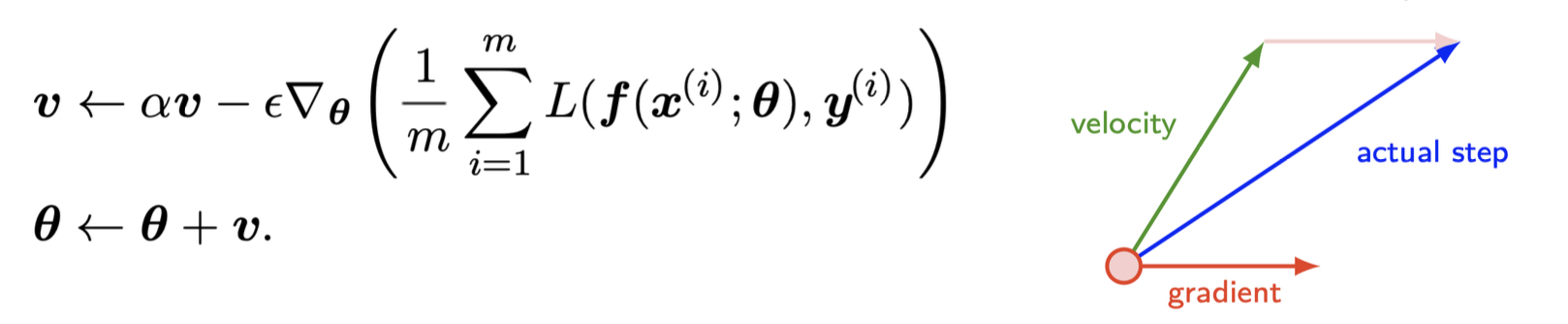
Momentum (cont.)

SGD + 모멘텀은 신경망 훈련을 가속화할 수 있다

때때로, 오버슈팅을 유발할 수 있다.

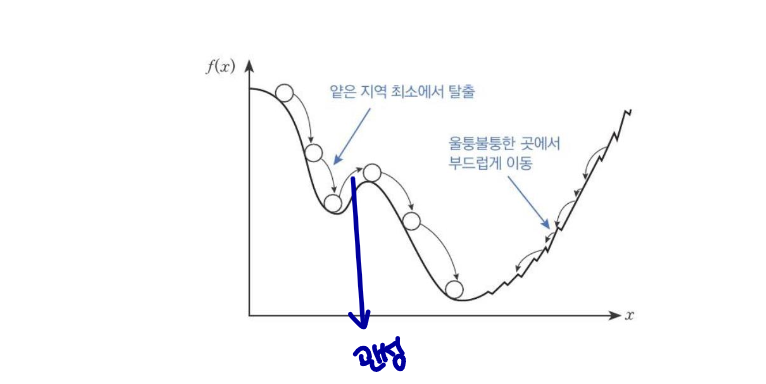
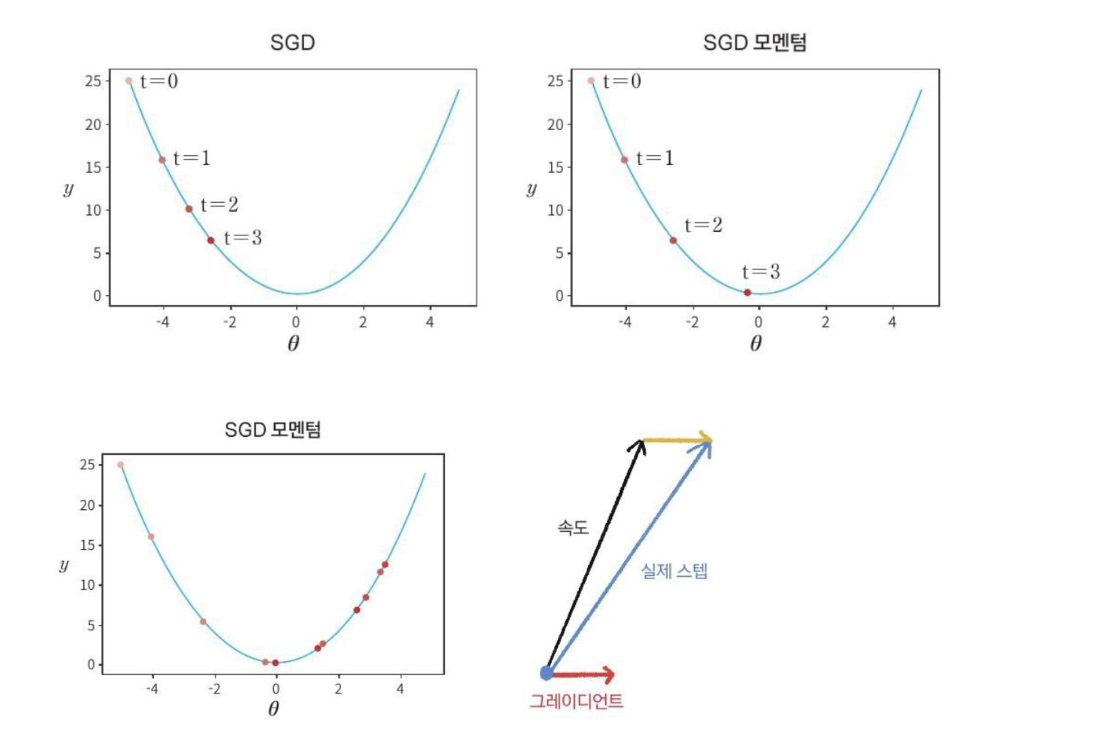
Nesterov Momentum

Nesterov Momentum

• 그레디언트는 현재 속도가 적용된 후에 평가된다.

• 모멘텀의 표준 방법에 대한 연관계수이다.

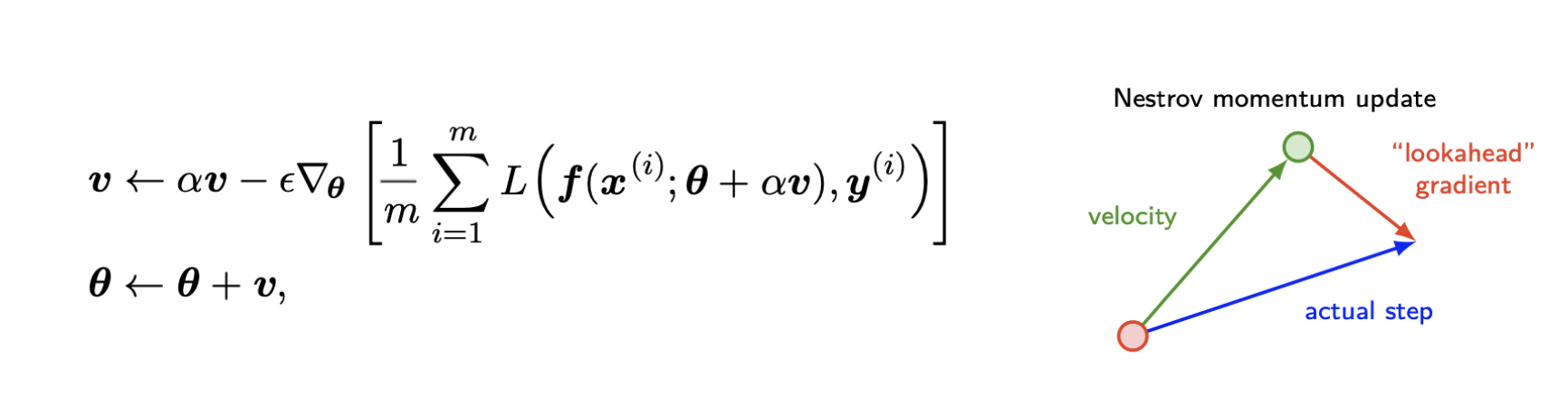
Adaptive Learning rates

이전 알고리즘은 학습 속도(learning rate)를 하이퍼 파라미터로 사용한다.

• 모든 매개변수에 대해 전역적으로 그리고 동일하게 설정한다.

• 모멘텀은 또 다른 하이퍼 파라미터를 도입한다.

학습 과정 전반에 걸쳐 각 매개 변수에 대한 학습 속도를 자동으로 조정한다.

• AdaGrad / RMSProp / Adam

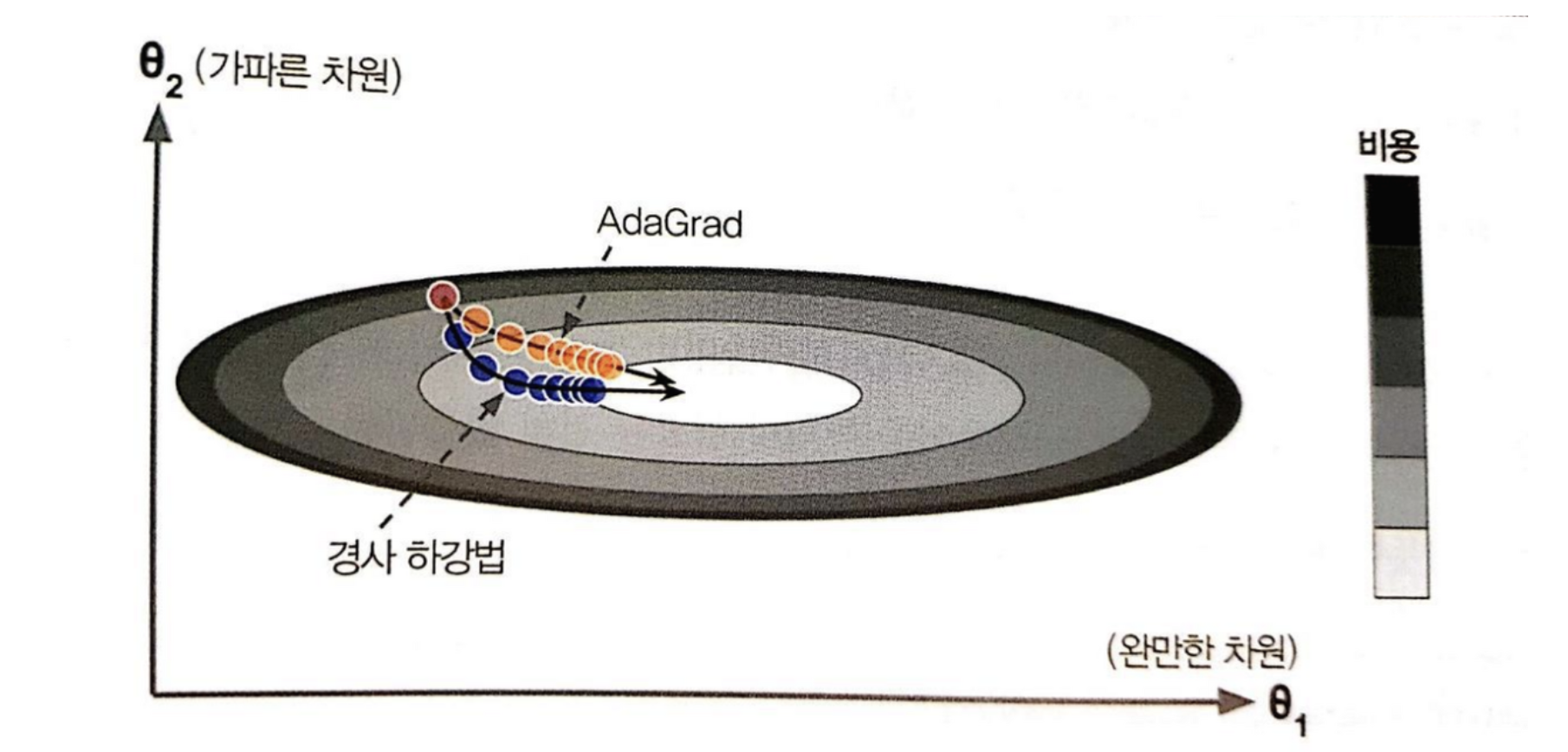
Gradient descent 알고리즘은 global minimum으로 곧장 향하지 않고 가장 가파른 경사를 따라 빠르게 내려가기 시작해서 골짜기 아래로 느리게 이동한다. AdaGrad 알고리즘은 global minimum의 방향을 좀 더 일찍 감지하고 global minimum쪽으로 좀더 정확한 방향을 잡아서 이동한다.

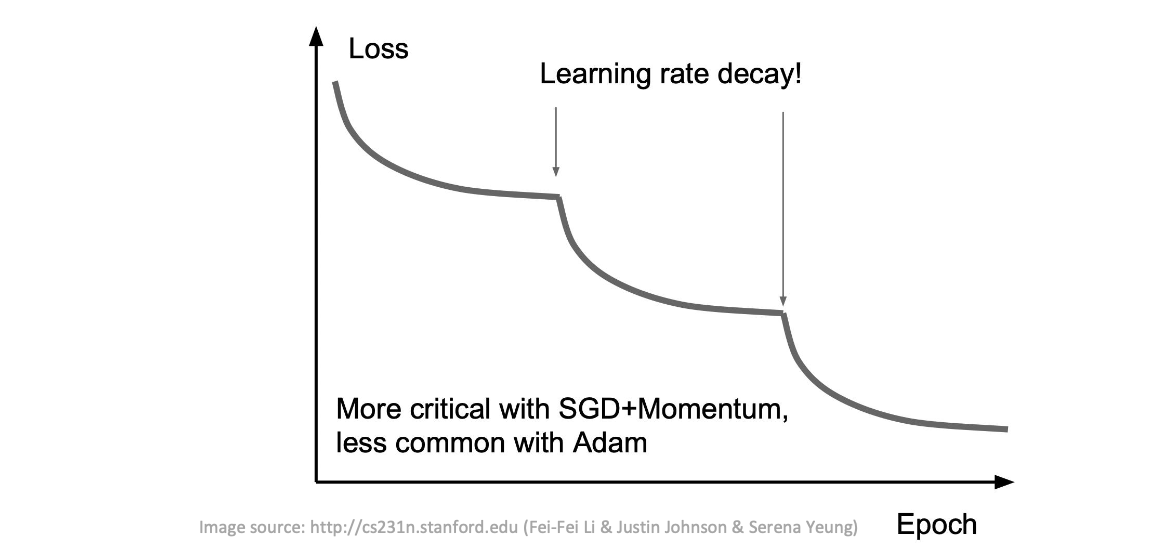
일반적인 Gradient descent 알고리즘의 경우에는, 모든 파라메터에 대해 동일한 step-size (학습률)가 적용된다. 이에 반해 Adaptive 방법은, 각각의 매개변수에 맞춰서 학습률을 변화시키는 학습을 진행하면서, 학습률을 점차 줄여가는 방법 이다. 학습률 감소시키는 기법인 learning rate decay와 비슷하다고 할 수 있다.

Adaptive Gradient (AdaGrad)

AdaGrad

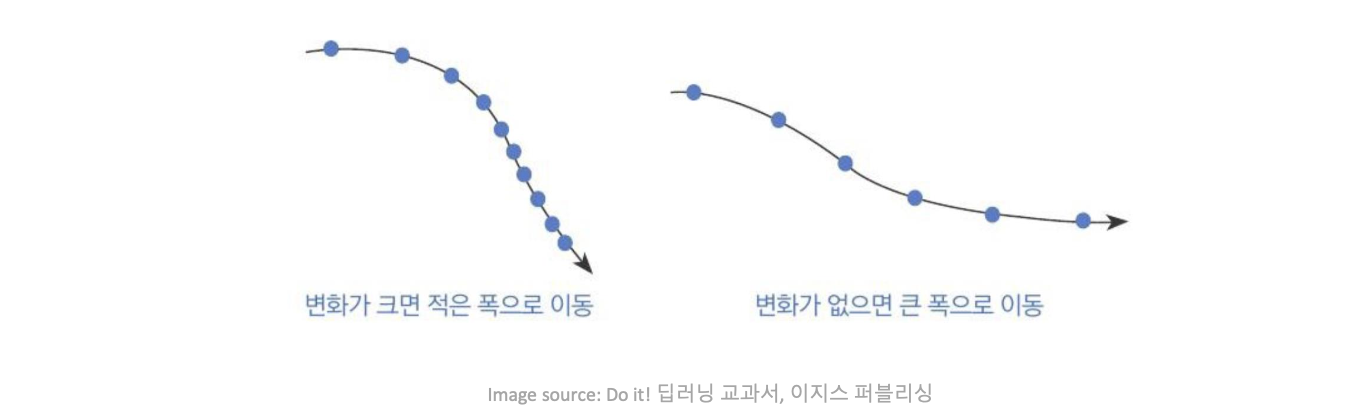
• 모든 과거 제곱 값의 합의 제곱근에 반비례하여 모든 모델 매개 변수의 학습 속도를 개별적으로 조정합니다.

• 손실의 가장 큰 편도함수는 그에 따라 학습 속도가 급격히 감소한다.

• 작은 편도함수는 학습률이 비교적 적게 감소한다.

• 순효과는 매개변수 공간의 더 완만하게 기울어진 방향에서 더 크게 진행되는 것이다.

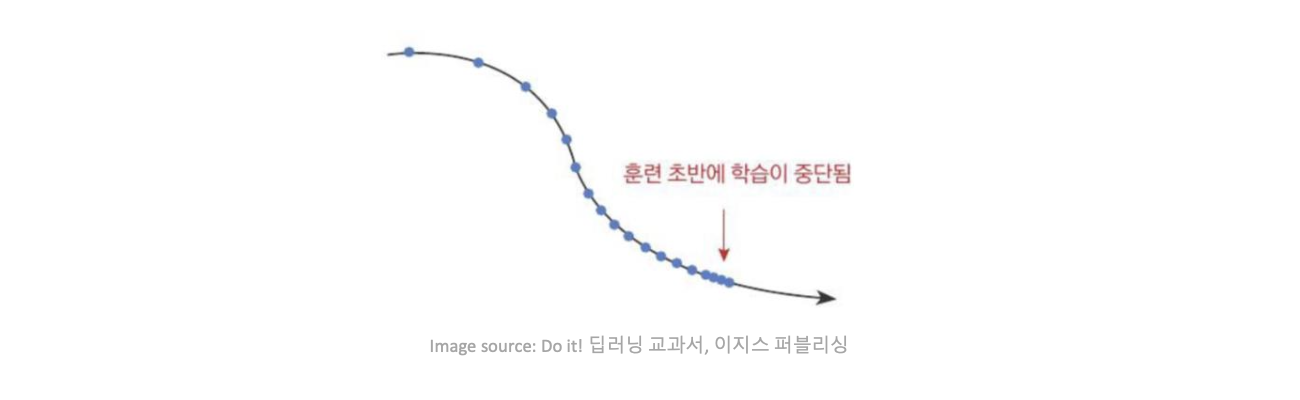
AdaGrad는 일부 딥러닝 모델에서 잘 수행되지만 모든 딥러닝 모델에 잘 적용되는 것은 아니다.

• AdaGrad는 볼록 함수에 적용할 때 빠르게 수렴하도록 설계되었다.

• 단조 감소는 너무 일찍 학습을 멈출 수 있다.

Root Mean Square Propagation (RMSProp)

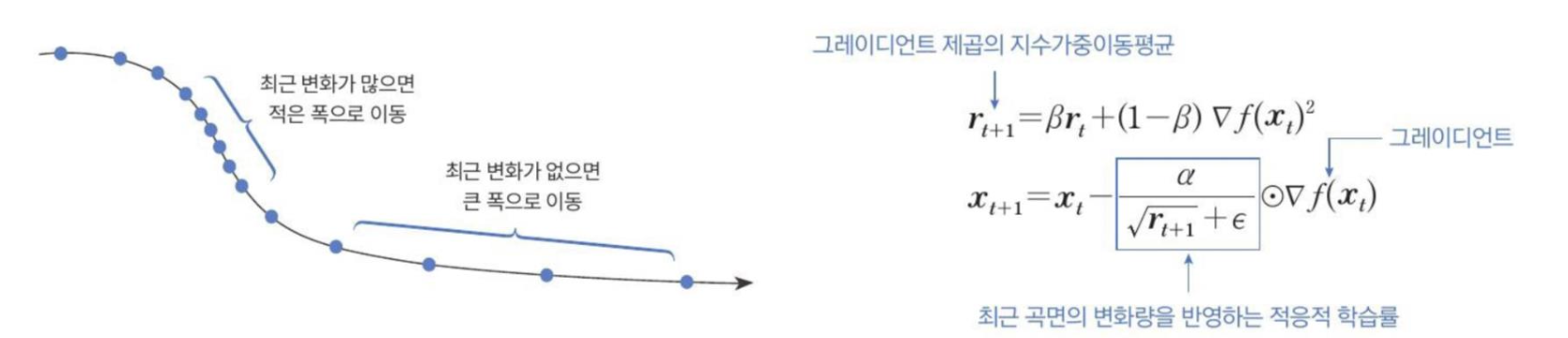
RMSProp

• 기울기 누적을 n 지수 가중 이동평균으로 변경하여 비볼록 설정에서 더 나은 성능을 발휘하도록 AdaGrad를 수정한 것이다.

• 볼록한 그릇을 찾은 후 빠르게 수렴할 수 있도록 극한 과거의 기록를 버린다.

  • 최근 변화가 많이 반영되고, 오래된 변화는 적게 반영된다.

• 심층 신경망을 위한 효과적이고 실용적인 최적화 알고리즘이다.

Adaptive Moment estimation (Adam)

Adam

• 적응형 (RMSprop) + momentum

• Bias 보정

• 일반적으로 공정하다고 간주된다.

  • 하이퍼 파라미터 선택에 강력하다.

Which algorithm should one choose?

안타깝게도 현재 이 점에 대한 합의가 이루어지지 않았다.

Adam은 사용할 기본 알고리즘으로 권장된다.

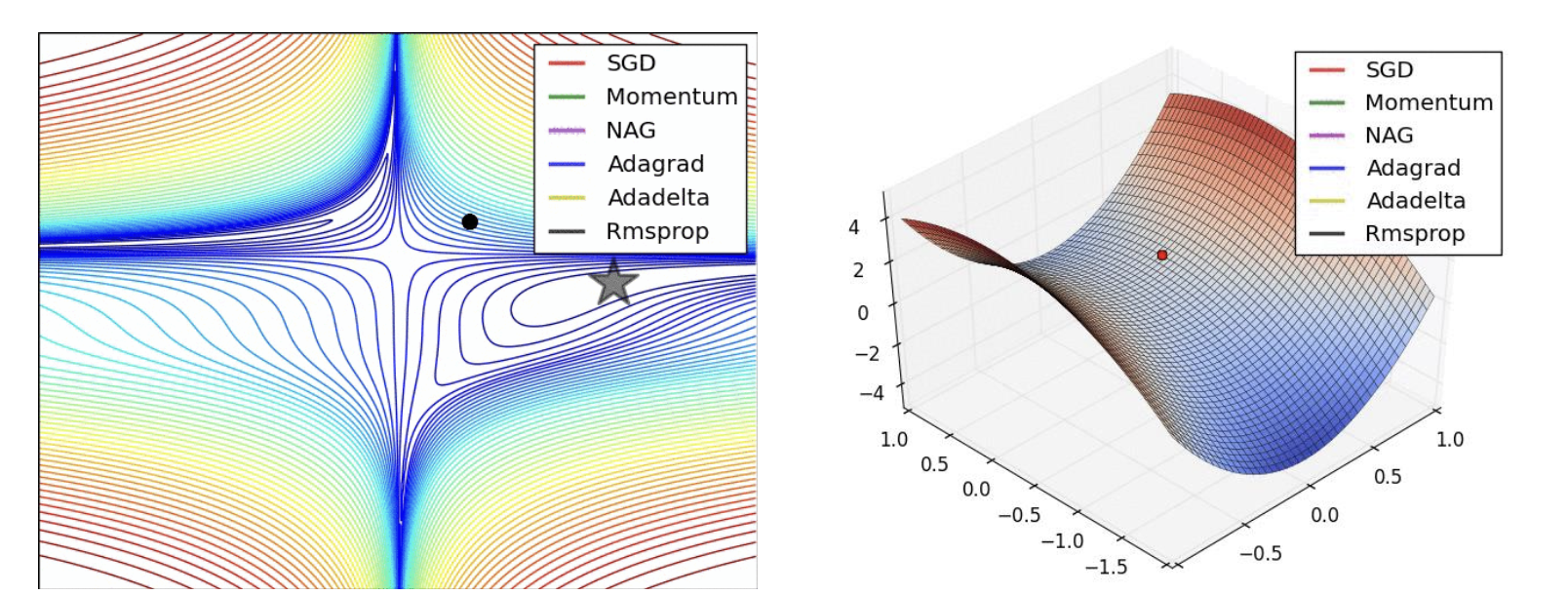
Which algorithm should one choose? (cont.)

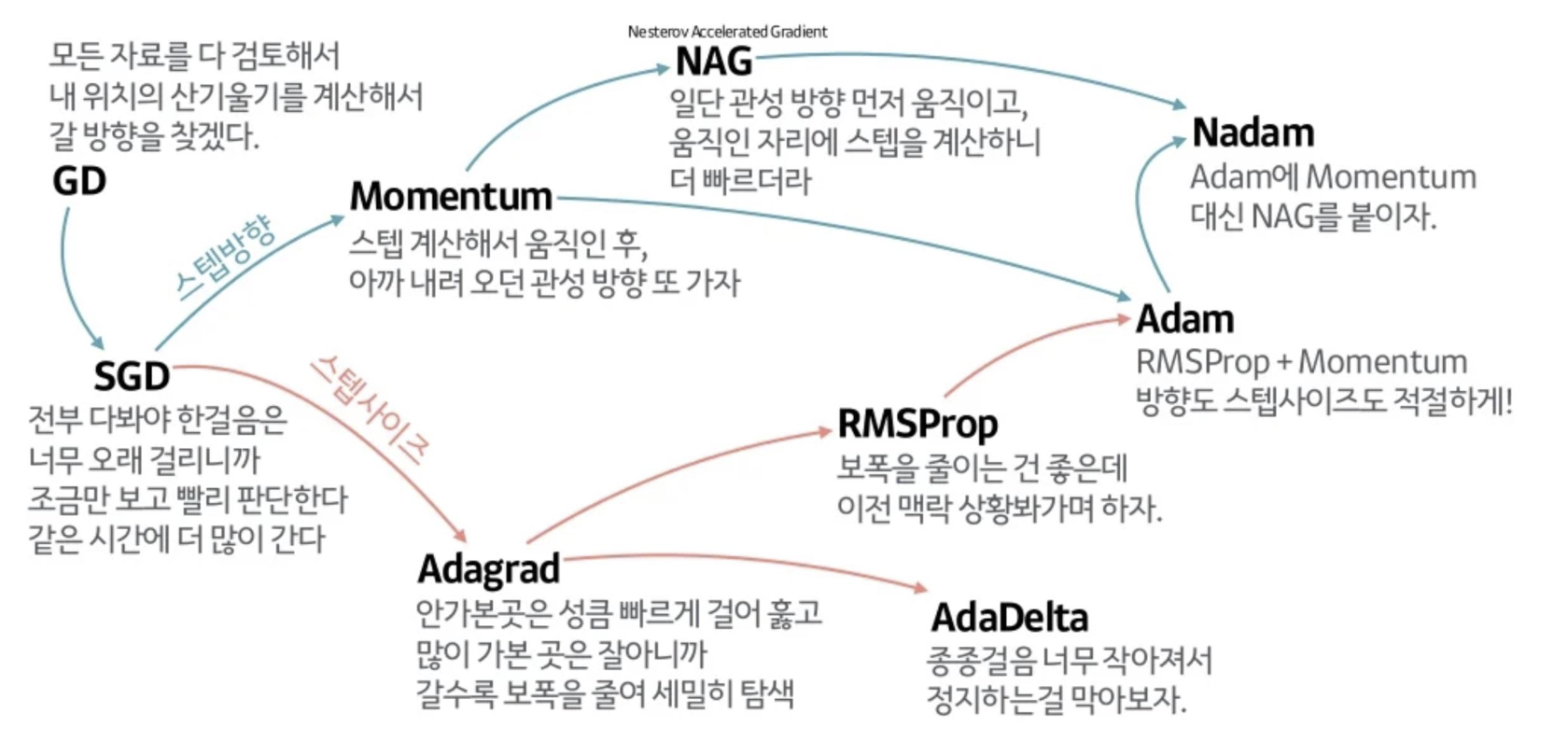
Learning rate

SGD, SGD+Momentum, Adagrad, RMSProp, Adam은 모두 하이퍼파라미터로 학습률을 갖는다.

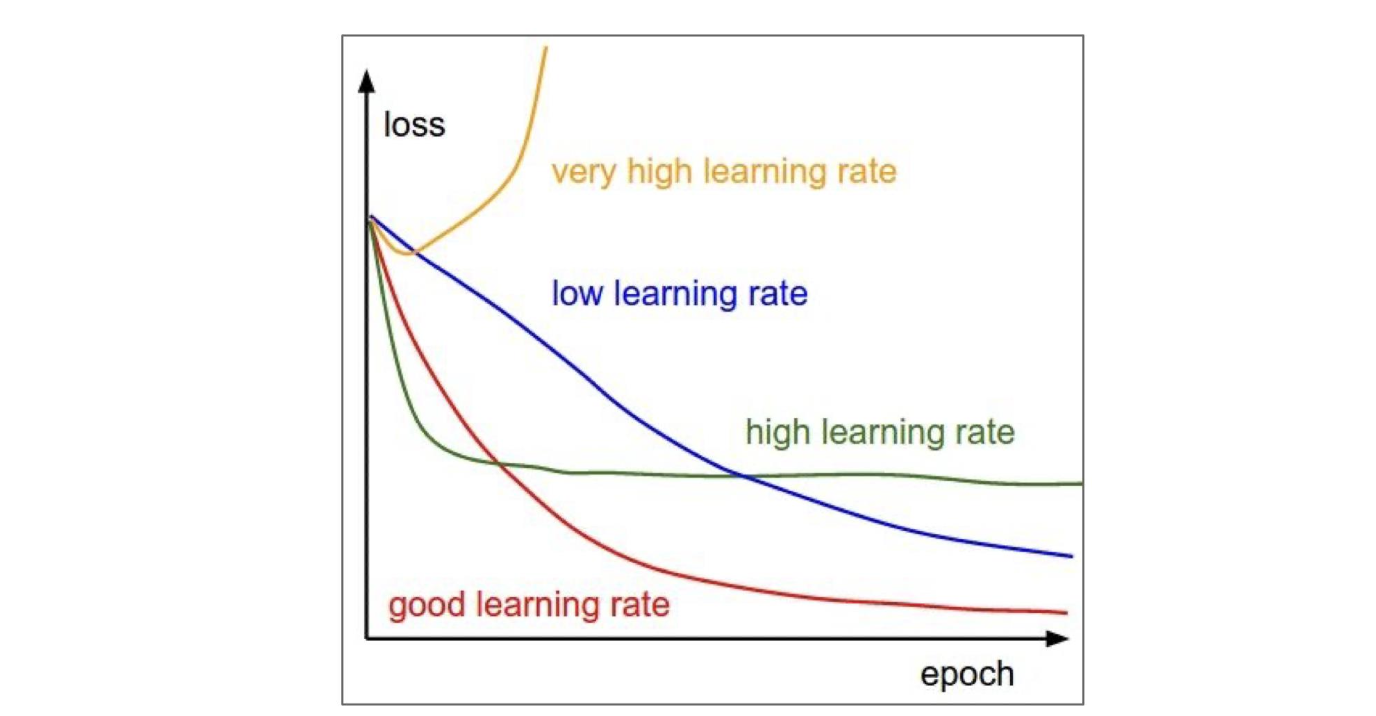
시간이 지남에 따라 점진적으로 학습 속도를 줄여나가야 함

• Step decay

• 1/t decay: 𝜖 = 𝜖0/(1 + 𝑘𝑡)

• Exponential(지수) decay: 𝜖 = 𝜖0Ф−𝑘𝑡