[논문리뷰] Aggregated Residual Transformations for Deep Neural Networks

ChangSeong Yoo·2025년 1월 31일

Deep Learning

목록 보기

10/12

📝 이번 포스트는 ResNeXt로 알려진 "Aggregated Residual Transformations for Deep Neural Networks" 논문에 대해 알아보도록 하겠습니다.

1. Why : 논문의 연구 배경

이 논문이 발표되기 전, VGGNet과 ResNet등 깊이가 깊어진 신경망들이 발표되었고, 높은 성능을 보였습니다.
그리고 Inception 모델도 발표되었는데, 이 모델은 깊이도 깊을 뿐만 아니라 wide한 특징을 갖는 모델로서 높은 성능을 보였습니다.
Inception 모델의 주요 특징은 "split-transform-merge" 방법으로, 이 방법을 통해 비교적으로 낮은 연산 비용을 가지면서도 강력한 성능을 보여주었습니다.
입력 데이터를 여러 낮은 크기의 합성곱(1x1, 3x3, 5x5)으로 분할(split)하고 합성곱 필터를 거친 뒤에 합병(concatenation)하는 과정을 거칩니다.
Inception 모델은 좋은 성능을 보였지만, 각 단계에서 모듈의 필터 수 와 크기를 각 상황에 맞게 조정해야 하는 설계의 복잡성이 있습니다.
이러한 모듈 속 조합이 좋은 성능을 보인다고 할지라도 새로운 데이터셋이나 작업에 적용될지는 불분명합니다.

저자는 이러한 Inception의 한계를 극복하기 위해 VGGNet/ResNet의 단순함과 Inception의 split-transform-merge 방법을 결합한 새로운 모델인 ResNeXt를 연구하게 되었습니다.

2. How : 연구 방법론

2.1. Template

저자는 Residual block들을 쌓은 구조를 기반으로 신경망을 구성하였습니다.
신경망 속 이 Residual block들은 모두 다 동일한 토폴로지를 갖습니다.
또한 VGGNet 과 ResNet의 영향을 받아 다음 두 가지 간단한 규칙을 따르도록 모델을 설계하였습니다.

동일한 크기의 spatial map을 출력으로 생성한다면, 블록들은 너비와 필터 크기를 공유한다.
즉, 같은 피쳐맵의 크기를 유지하는 계층에서는 동일한 필터 크기와 채널 수를 사용하여 일관성을 유지하게 합니다.
spatial map이 2의 배수로 다운샘플링 된다면, 블록들의 너비가 2의 배수로 증가한다.
즉, 피쳐맵이 줄어든만큼 채널 수를 증가시켜야 한다는 것입니다.

이 두 가지 규칙을 따른다면, 네트워크 전체를 단 하나의 템플릿 모듈(=토폴로지)만으로 설계할 수 있습니다.
이 템플릿 모듈을 기반으로 모든 블록은 자동으로 결정됩니다.

2.2. Revisiting Simple Neurons

딥러닝에서 가장 기본적인 연산은 내적(inner product)입니다.
FC-layer와 Conv layer 모두 이 내적 연산을 기반으로 작동하며, 내적의 수식은 아래와 같습니다.

\sum^{D}_{i=1} w_i x_i

$x = [x_1, x_2, \dots, x_D]$ : $D$ 채널의 입력 벡터
$w_i$ : $i$ 번쨰 채널의 가중치

내적을 그림으로 도식화해 보면 아래와 같습니다.

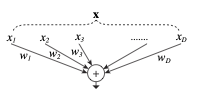
위 그림을 보면 하나의 뉴런이 여러 입력값(split)을 입력받아 특정 방식으로 변환(transform) 후 합치는(aggregate) 과정으로 볼 수 있습니다.

이러한 관점에서 보면, 뉴련의 기본 동작도 ResNeXt의 split-transform-aggregate 전략과 유사한 방식으로 설명될 수 있다는 것을 보여줍니다.

2.3. Aggregated Transformations

저자는 기존 신경망에서 뉴런이 수행하는 단순한 연산인 $w_i x_i$ 을 대체할 새로운 방법을 연구하였습니다.
대체할 새로운 방법이 하나의 네트워크가 되게끔 하는 복잡한 연산 방법을 모색하였습니다.
저자는 깊이와 너비를 증가시키는 Network In Network 논문과 다르게 새로운 차원으로 확장하는 "Network-in-Neuron" 방법을 연구하였습니다.
저자의 방법을 수식으로 표현하면 아래와 같습니다.

F(x) = \sum^{C}_{i=1}T_i(x)

$C$ : Caridnality, 집계(aggregate)되는 변환(transformation)의 개수
$T_i(x)$ : 변환 함수

$\sum^{D}_{i=1} w_i x_i$ 의 D(dimension) 대신 C(cardinality)를 사용하는 것은 모델의 성능이 향상하며, 깊이나 너비를 증가시키는 것보다 효과적임을 실험적으로 증명하였다고 합니다.
해당 실험은 추후 3.Experiment 파트에서 설명하겠습니다.
저자는 모든 $T_i(x)$ 를 같은 토폴로지로 구성해야 한다고 합니다.
그 이유는, 토폴로지를 같게 설정함으로써 단순하면서도 효율적인 확장성을 가질 수 있기 때문입니다.

게다가 저자는 ResNet의 Residual connection을 자신의 모델에 구현하였습니다.
Residual connection을 반영한 식은 아래와 같습니다.

y = x + \sum^{C}_{i=1}T_i(x)

위 식을 아래 그림의 (a)로 나타낼 수 있습니다.

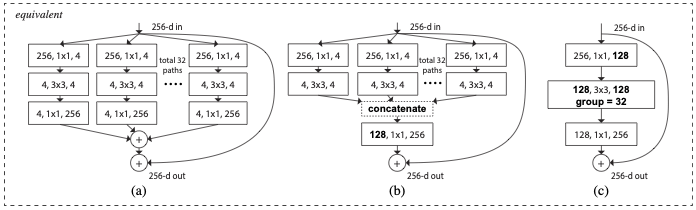
그림 (a) 속 total 32 paths는 cardinality를 32로 설정하였다는 뜻입니다.
얼핏 보면 Inception 모델들처럼 모듈 속 여러 path를 갖는 유사한 구조입니다.
하지만 다른 점은 Inception 모듈 속 path는 각각 다른 형태를 보이지만, ResNeXt의 모듈 속 path는 모두 동일한 토폴로지를 갖는다는 점입니다.

Relation to Inception-ResNet
위 그림의 (b)는 Inception-ResNet 모듈과 유사한 구조입니다.
참고로 (b) 구조는 (a) 구조와 동일한 파라미터 수를 갖습니다.
(b)는 각 path의 출력 채널이 4이고 32가지의 path를 concatenation하여 출력채널을 128로 집계하는 방법입니다.
그다음 identity mapping의 출력 채널 수를 맞춰주기 위해서 1x1 합성곱으로 출력 채널 수를 256으로 증가시킵니다.
그러면 (a)와 같아집니다.
위에서 말했듯, Inception-ResNet 역시 다중 path를 활용하지만, 각 path가 서로 다른 형태의 변환을 수행한다는 것입니다.
하지만 Inception-ResNet 모듈과 다르게 ResNeXt는 모든 path들이 동일한 토폴로지를 갖는다는 것입니다.
따라서 위 구조의 장점은 최소한의 디자인 노력으로 훨씬 단순하고 다른 데이터셋에 적용하기가 쉽다는 것입니다.

Relation to Grouped Convolutions
위 그림의 (c)는 Grouped Convolution 개념과 유사한 구조입니다.
(c)의 방법대로라면 $T_i(x)$ 의 합성곱 레이어를 큰 단일 레이어로 대체하고 여러 path로 나누지 않고 입력채널을 여러 개의 그룹으로 나누어 처리할 수 있습니다.
group convolution은 여러 개의 그룹으로 나누어 학습하는 방법으로, AlexNet에서 구현되었던 방법입니다.

group convolution이란?
input의 채널을 여러 개의 그룹으로 나누어 독립적으로 연산을 수행하는 방식
장점 :
1. 병렬처리에 특화
2. 일반 합성곱보다 더 적은 파라미터로 학습 가능
3. 각 그룹에 더 높은 correlation을 갖는 채널이 학습 가능

참고로 group convolution으로 구현한 (c) 구조는 (a)와 (b) 구조와 동일한 것입니다.
32개의 그룹으로 나누었으니 각 그룹의 출력채널은 4가 될 것입니다.
그다음 concatenation으로 각 그룹의 출력채널을 집계한 후, 1x1 합성곱으로 residual connection할 채널 수와 같게 맞춰주면 됩니다.

group convolution을 활용한 방법이 계산량을 줄이고 구현을 더 단순하게 만들어줄 수 있지만, 블록의 깊이가 3 이상일 때 효과적이라고 합니다.

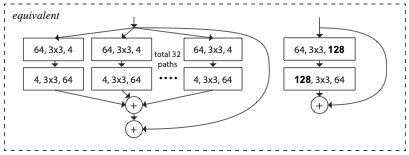
위 그림을 보면 깊이가 2일 때의 상황입니다.
group convolution으로 병목현상을 구현할 수가 없습니다.

2.4. Model Capacity

저자는 Cardinality를 변화시키면서 어떻게 성능이 달라지는지 비교할 때, 다른 하이퍼파라미터는 고정하고 실험을 진행해야 한다고 합니다.
ResNeXt의 Bottleneck 블록의 파라미터 수는 다음과 같이 계산됩니다.

C \cdot (256 \cdot d + 3 \cdot 3 \cdot d \cdot d + d \cdot 256)

C는 cardinality를 뜻하고, d는 Bottleneck의 width를 뜻합니다.

"3. Experiments"에서 ResNet과 비교하는 실험이 나오는데, 참고할 테이블과 그림들은 실험 부분에서 다루겠습니다.

3. Experiments

3.1. Cardinality vs Width

위의 구조 (a), (b), (c)가 설명되었습니다.
저자는 3가지 구조를 비교하여 어떠한 구조가 효율적인지 비교실험을 진행하였습니다.
결과는 Grouped Convolution 방법으로 구현한 (c) 구조가 연산 속도 면에서 빨랐다고 합니다.
(a)와 (b)와 (c) 모두 같은 파라미터 수를 갖지만 입력 벡터의 채널을 그룹으로 나누어 진행하는 (c) 구조가 가장 빨랐다고 합니다.
따라서 추후 실험에서 사용한 ResNeXt는 (c) 구조로 구현한 ResNeXt라고 합니다.

저자는 위 테이블의 세팅을 따라서 cardinality와 bottleneck의 width를 변경하면서 최적의 cardinality와 bottleneck width를 찾기 위해 실험을 진행하였습니다.

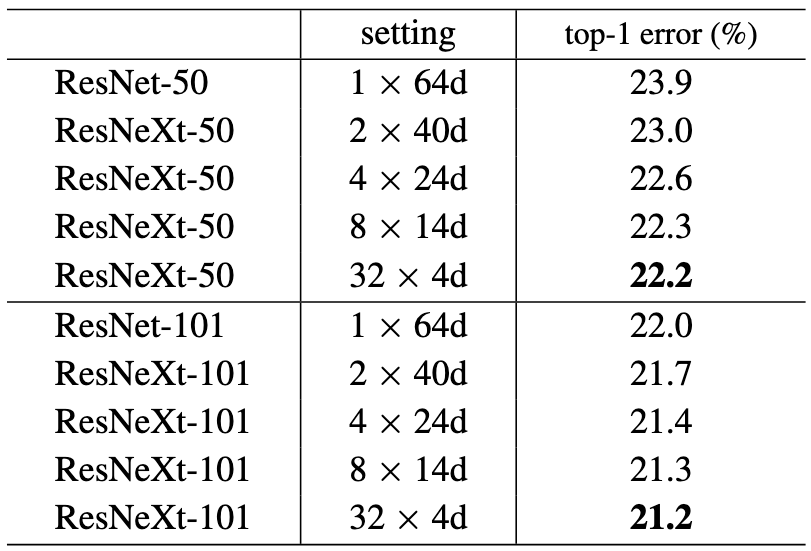
ResNet과 비교하여 cardinality 개념을 도입한 모든 ResNeXt 모델들이 낮은 top-1 error를 보였지만 cardinality=32, d(bottleneck width)=4일 때 가장 낮은 에러율을 보였습니다.
레이어 수가 50일 때와 레이어 수가 101일 때 둘 다 cardinality=32, d=4일 때 가장 낮은 top-1 error를 보였습니다.
따라서 뒤에 나오는 모든 실험은 cardinality=32, d=4로 설정한 ResNeXt으로 실험을 진행하였다고 합니다.

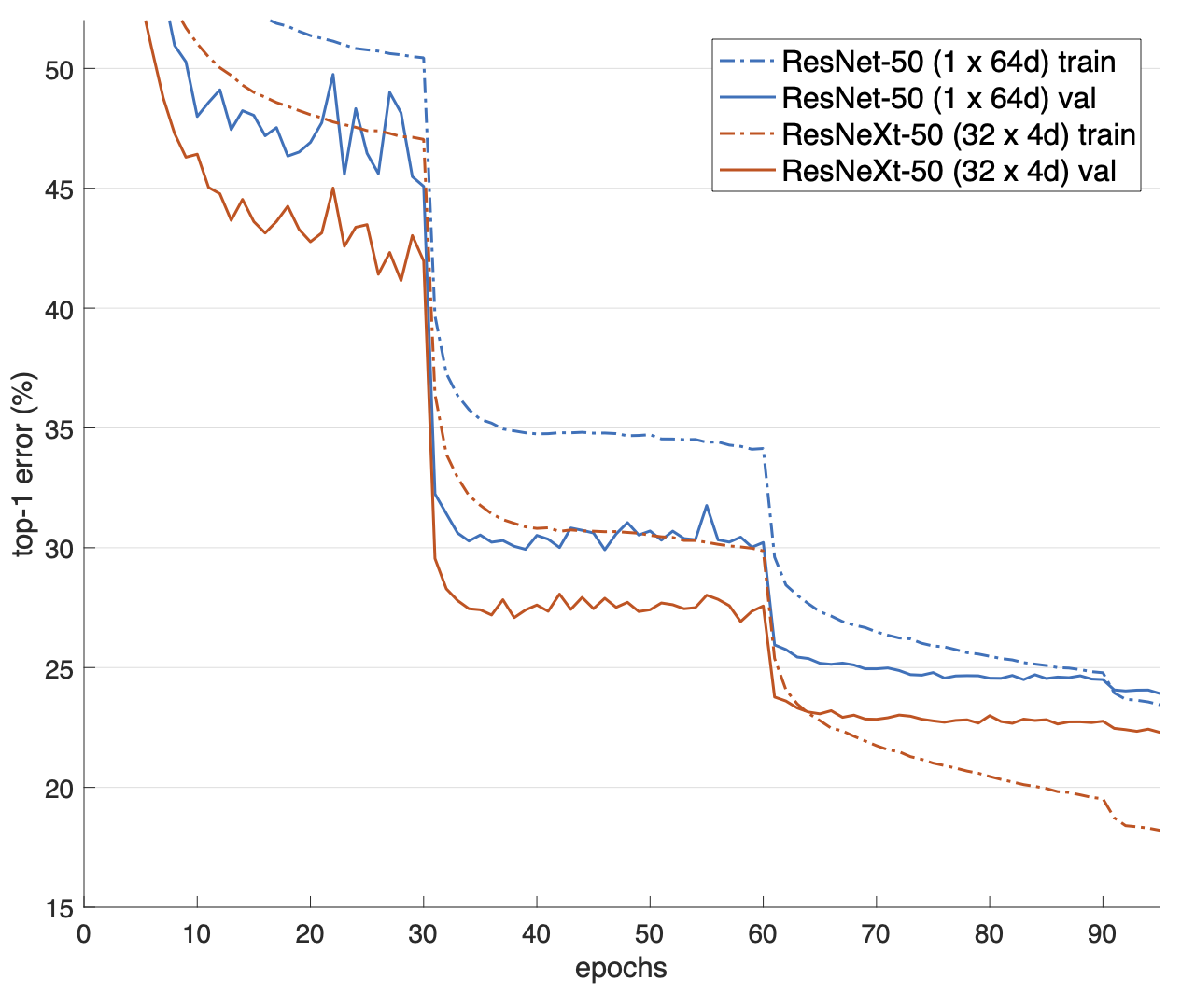
cardinality=1, d=64로 설정하면 기본적인 ResNet이 됩니다.
위 그림은 cardinality=1, d=64인 경우와 cardinality=32, d=4인 경우를 비교한 실험입니다.
cardinality=32, d=4로 설정했을 경우가 더 빠른 속도로 top-1 error가 감소함을 볼 수 있습니다.

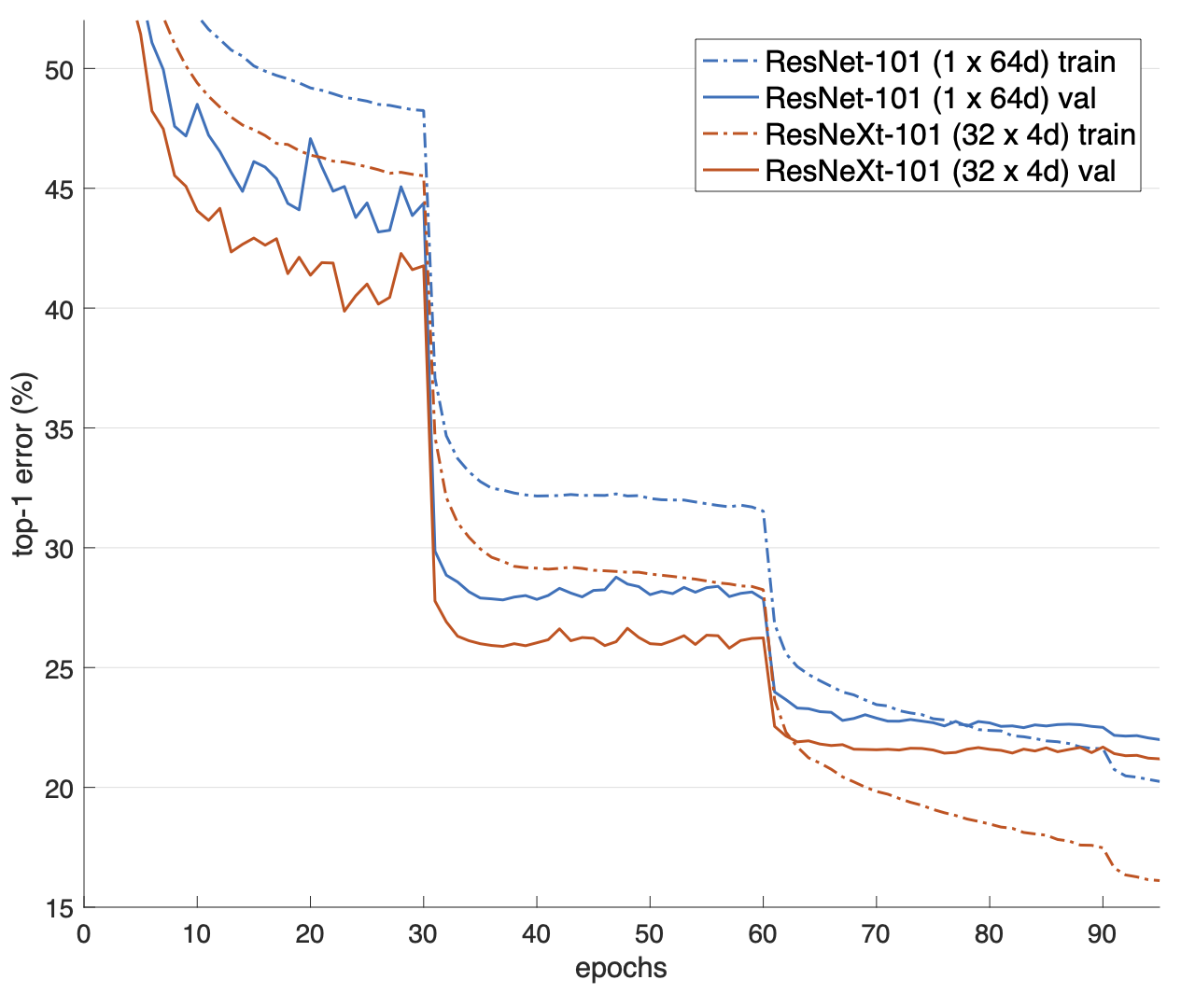
위 실험은 레이어 수가 101인 경우로 다른 조건들은 동일하게 한 실험입니다.
레이어 수가 101일 때 또한 cardinality=32, d=4인 경우가 더 빠른 속도로 top-1 error가 감소함을 볼 수 있었습니다.

3.2. Increasing Cardinality vs Deeper/Wider

이 실험은 깊이를 증가시키는 것과 너비를 증가시키는 것에 비해 Cardinality를 증가시키는 것이 훨씬 효율적임을 확인하기 위한 실험입니다.

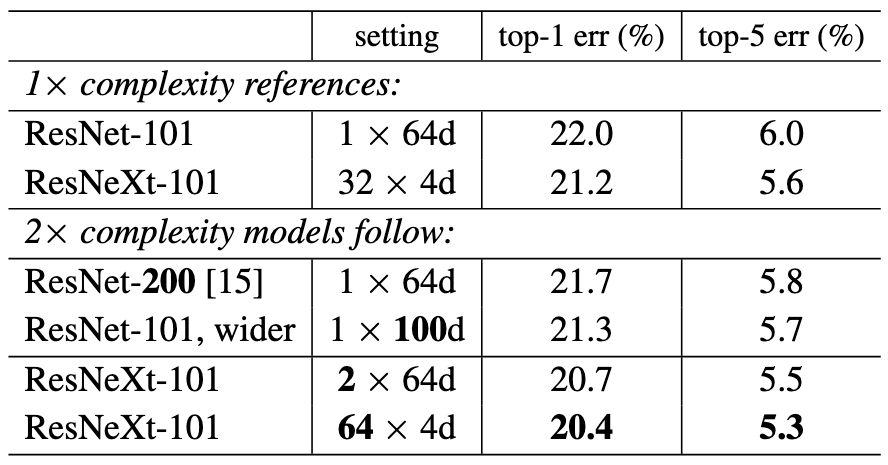
위 표를 보면 깊이를 약 두 배 증가시킨 ResNet-200의 에러율이 깊이를 증가시켰음에도 불구하고 ResNeXt-101보다 높음을 볼 수 있습니다.
그다음, 더 wide한 ResNet-101의 에러율이 더 wide했음에도 불구하고 ResNeXt보다 에러율이 높음을 볼 수 있습니다.
따라서 이 실험으로 cardinality가 깊이와 너비보다 더 학습에 효율적임을 알 수 있습니다.

4. Conclusion

Cardinality가 딥러닝 모델 설계에서 깊이와 너비보다 더 중요한 하이퍼파라미터로 작용할 수 있음을 알 수 있었습니다.
ResNet을 기반으로 설계한 ResNeXt는 깊이를 증가시키지 않고도 Cardinality라는 개념으로 성능을 개선할 수 있었습니다.

ChangSeong Yoo

𝒥𝓊𝓃𝒾ℴ𝓇 𝒟𝒶𝓉𝒶 𝒮𝒸𝒾ℯ𝓃𝓉𝒾𝓈𝓉

이전 포스트

[논문리뷰] Densely Connected Convolutional Networks

다음 포스트