📝 이번 포스트는 MobileNet으로 알려진 "MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications" 논문에 대해 알아보도록 하겠습니다.

1. Why : 논문의 연구 배경

이전 연구들은 CNN을 더 깊고 복잡하게 만듦으로써 정확도를 높이는 데 성공하였습니다.
하지만 이러한 접근 방식은 latency와 accuracy를 trade-off함으로써 accuracy가 향상할 수 있었던 것입니다.
로보틱스나 자율주행, 증강현실과 같은 실제 응용 분야에서는 연산 자원이 제한된 상태에서 시간 안에 작업을 끝내는 것이 중요하게 여겨집니다.
최신 SOTA 모델들은 accuracy는 충분히 좋지만, 실제 현장에서 요구하는 latency를 충족하지 못합니다.
저자는 이러한 문제를 해결하기 위해 Depthwise Separable Convolution 개념을 활용하여, 크기가 작고 latency가 작은 모델을 개발하기 위해 연구하였습니다.

---

2. How : 연구 방법론

2.1. Depthwise Separable Convolution

저자는 연산 비용을 줄이고 실행 시간을 단축하기 위해 표준 합성곱 방식을 대체할 방법을 연구하였습니다.
저자는 표준 합성곱을 Depthwise Convolution과 Pointwise Convolution 두 단계로 분리하여 연산을 수행하는 Depthwise Separable Convolution을 제시하였습니다.
이 방법은 Depthwise Convolution을 수행한 후 Pointwise Convolution을 수행하는 방식입니다.

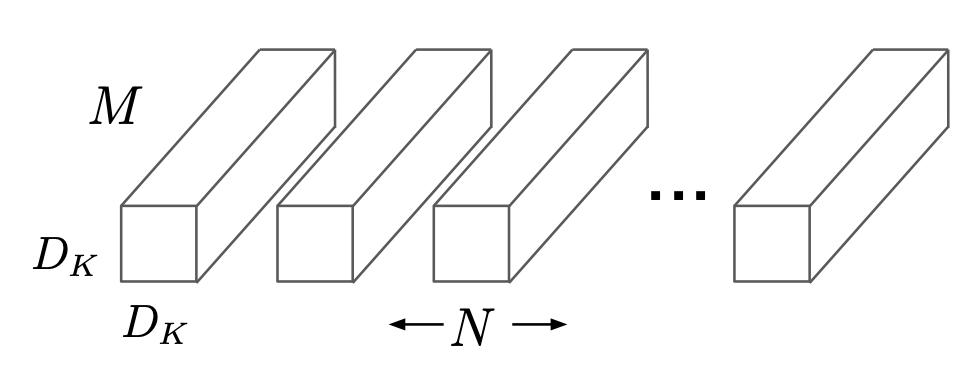
위 그림은 표준 합성곱을 그림으로 나타낸 것입니다.
표준 합성곱의 연산 비용을 구하는 식은 아래와 같습니다.

$D_F$ : 입력 피쳐맵의 크기
$M$ : 입력 채널 수
$D_G$ : 출력 피쳐 맵의 크기
$N$ : 출력 채널 수
$D_K$ : 필터(=커널)의 크기

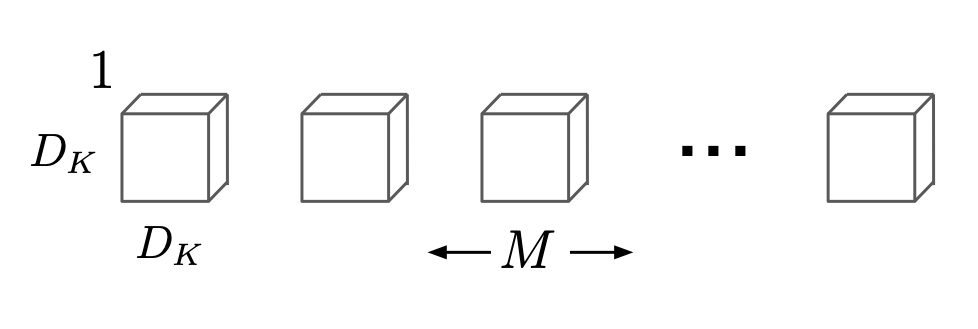
위 그림은 Depthwise Convolution을 그림으로 나타낸 것입니다.
Depthwise Convolution의 연산 비용을 구하는 식은 아래와 같습니다.

각 입력 채널에 대해 하나의 필터를 적용하여 독립적으로 피쳐를 추출합니다.
하나의 필터를 적용하기 때문에 입력의 채널 수와 출력의 채널 수는 동일할 것입니다.

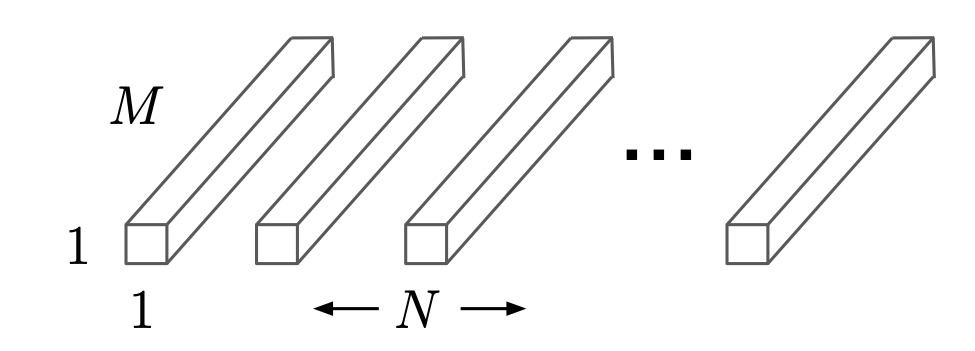
위 그림은 Pointwise Convolution을 그림으로 나타낸 것입니다.
Depthwise Convolution을 진행하였으니, 다음으로 Pointwise Convolution을 진행해야 합니다.
Pointwise Convolution의 연산 비용을 구하는 식은 아래와 같습니다.
Pointwise Convolution은 1x1 합성곱으로, 차원 축소의 역할을 합니다.

Depthwise Separable Convolution의 총연산 비용은 아래와 같습니다.

이를 표준 합성곱으로 나누면 아래와 같아집니다.

$D_K$는 필터의 크기이고 주로 $D_K=3$으로 이용합니다. 그리고 출력 채널 수 $N$은 $D_K$에 비해 상당히 큰 숫자이므로 무시될 수 있습니다.
따라서 $D_K=3$이라고 가정하면 대략 9배 적은 연산량으로 같은 성능을 보일 수 있습니다.

2.2. Network Structure and Training

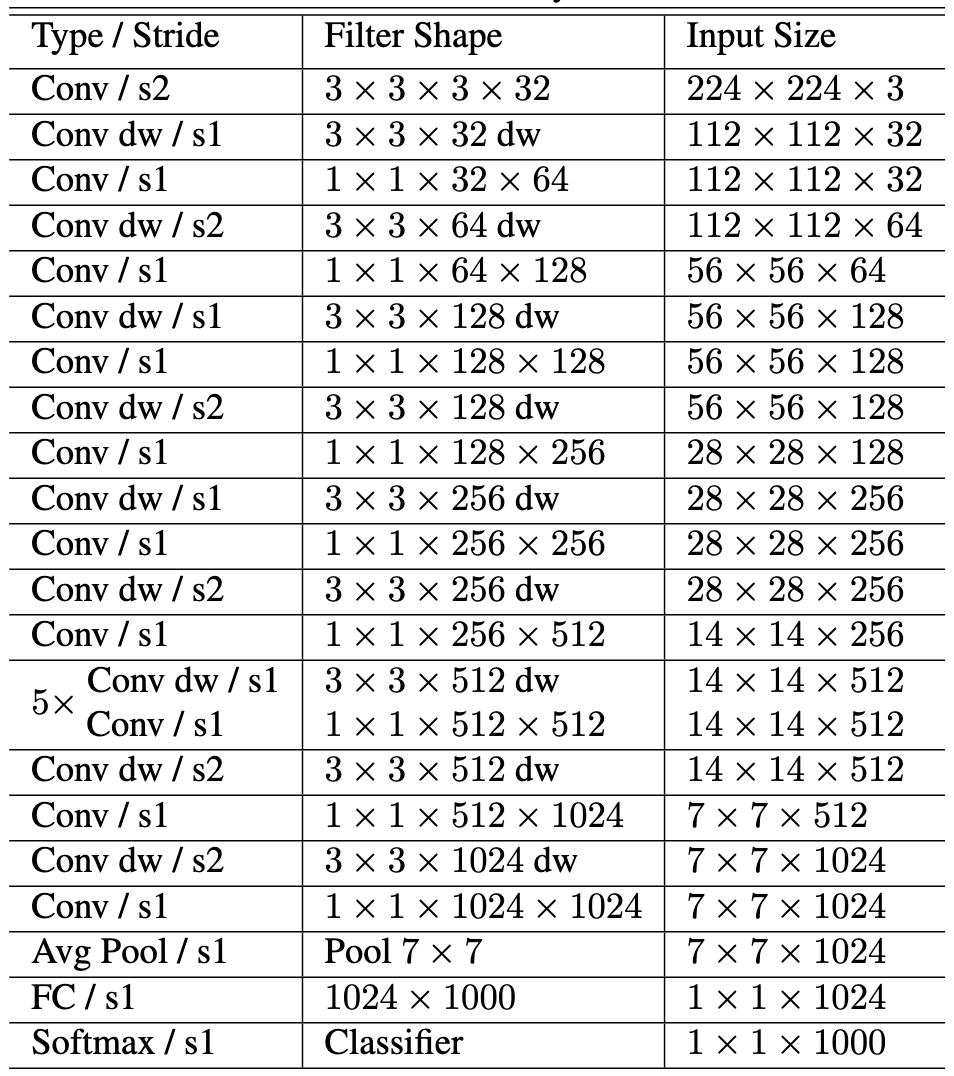
전반적인 MobileNet의 구조는 위와 같습니다.

첫 번째 층은 표준 합성곱으로 이루어져 있습니다.
그 뒤의 레이어들은 Depthwise Convolution & Pointwise Convolution으로 이루어져 있습니다.

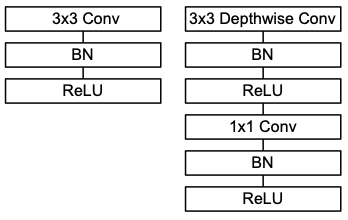
그리고 위 그림의 오른쪽과 같이 매 Depthwise Convolution과 Pointwise Convolution 뒤 Batch Normalization과 ReLU를 적용하여 학습 안정성을 높였습니다.
위 그림의 왼쪽은 표준 컨볼루션인데, 상식을 따랐다고 볼 수 있습니다.
모델의 마지막 부분의 Average Pooling과 FC layer와 Softmax에서는 Batch Normalization과 ReLU가 적용되지 않습니다.

2.3. Width Multiplier: Thinner Models

저자는 각 레이어의 채널 수를 줄이기 위한 방법을 연구하였습니다.
Width multiplier $\alpha$를 고려하면 채널 수를 일정 비율로 줄일 수 있었습니다.
입력채널 수는 $\alpha M$로 설정하고 출력채널 수도 $\alpha N$으로 설정합니다.

Width multiplier를 고려한 Depthwise Separable Convolution의 연산 비용을 구하는 공식은 아래와 같습니다.

$\alpha$의 범위는 [0, 1]이며 일반적으로 1, 0.75, 0.5, 0.25로 사용합니다.
Width multiplier를 고려함으로써 연산 비용이 $\alpha^2$와 비례하게 감소합니다.
MobileNet은 이미 경량화된 모델이지만, Width multiplier를 적용함으로써 모델 크기를 추가로 감소시킬 수 있습니다.
실행 시간과 크기의 교환으로 일어날 수 있는 일이지만 더 적은 실행 시간을 요구하는 환경에서는 이러한 구현이 필요할 수 있습니다.

2.4. Resolution Multiplier: Reduced Representation

저자는 연산 비용을 줄이기 위한 또 다른 방법을 연구하였습니다.
Resolution multiplier $\rho$를 고려하면 피쳐맵 크기를 조정하여 연산 비용을 줄일 수 있었습니다.
Resolution multiplier고 Width multiplier를 고려한 Depthwise Separable Convolution의 연산 비용을 구하는 공식은 아래와 같습니다.

$\rho$의 범위는 [0, 1]이며 $\rho < 1$ 로 설정하여 피쳐맵의 크기를 줄입니다.
Resolution multiplier를 고려함으로써 연산 비용이 $\rho^2$와 비례하게 감소합니다.

—

3. Experiments

위 표는 Standard Convolution으로 구성된 MobileNet과 Depthwise Separable Convolution으로 구성된 MobileNet의 비교실험입니다.
Depthwise Separable Convolution으로 구성된 MobileNet의 정확도는 약 1% 정도 감소했지만, 그 이상의 9배 정도 되는 연산량 감소율과 파라미터 감소율을 보여주었습니다.
정확도가 1% 감소한 것에 비해서 엄청난 trade-off를 보여주었습니다.

그다음 실험은 층의 수가 적은 Shallow MobileNet과 Width Multiplier $\alpha=0.75$의 MobileNet의 비교실험입니다.
층을 줄이는 것보다 채널 수를 줄이는 것이 연산 비용과 파라미터 수가 동일할 때 더 높은 정확도를 볼 수 있습니다.

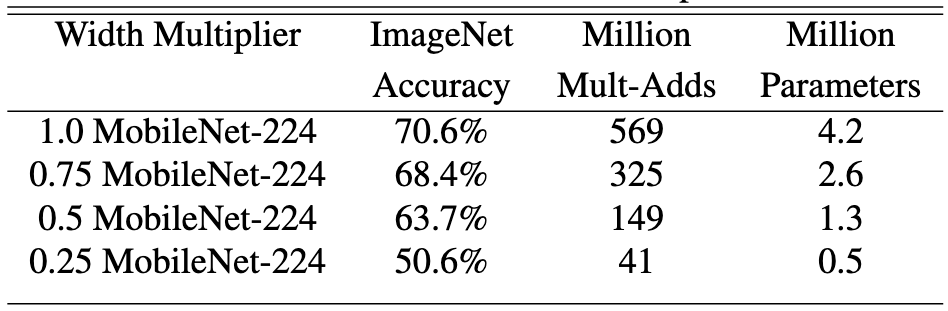
위 실험은 Width multiplier $\alpha$의 변화가 정확도와 연산 비용에 어떤 변화를 주는지 살펴보기 위한 실험입니다.
파라미터 수는 절반씩 줄어들지만 정확도 감소 폭은 그에 비해 작은 편임을 확인할 수 있습니다.

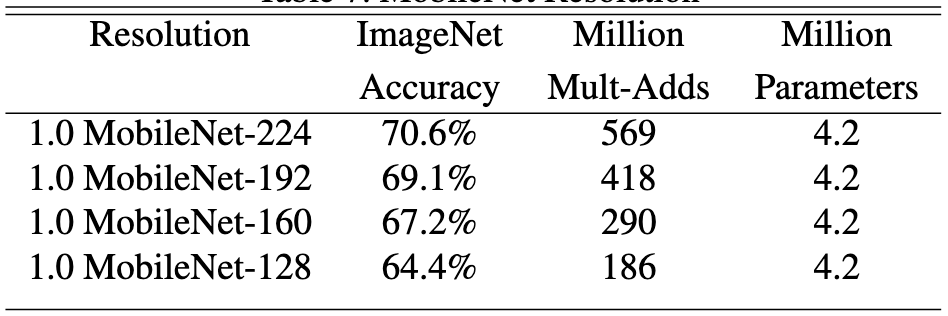
위 실험은 Resolution multiplier $\rho$에 변화를 주면서 정확도와 연산 비용에 어떤 변화를 주는지 살펴보기 위한 실험입니다.
연산 비용은 대폭 줄어들지만 정확도는 그에 비해 변화폭이 작음을 확인할 수 있습니다.

—

4. Conclusion

Depthwise Separable Convolution을 기반으로 한 MobileNets은 경량화와 연산 효율성을 극대화하는 것을 목표로 연구되었습니다.
Width multiplier($\alpha$)와 Resolution multiplier($\rho$)를 활용하여 모델의 크기와 속도를 조절하는 방법을 제시하였으며, 이를 통해 정확도를 일정 수준에서 유지하면서도 메모리 사용량과 지연 시간을 대폭 줄일 수 있음을 증명하였습니다.