📝 이번 포스트는 ResNet으로 알려진 "Deep Residual Learning for Image Recognition" 논문에 대해 알아보도록 하겠습니다.

1. Why : 논문의 연구 배경

층을 깊게 쌓은 Deep CNN은 이미지 분류 작업에서 지속적인 발전을 이끌었습니다.
깊이의 중요성에 따라 "더 나은 네트워크를 학습하는 것이 단순히 layer를 더 쌓는 것만으로 가능할까?"라는 질문이 뒤따르게 되었습니다.
층을 깊이 쌓는 것은 기울기 소실(vansihing gradient)과 기울기 폭등(exploding gradient) 문제를 야기합니다.
이 문제점은 normalization으로 대부분 해결할 수 있게 되었습니다.
normalization으로 인해 수십 개 층을 가진 네트워크도 SGD optimzer와 역전파를 통해 수렴할 수 있게 되었습니다.☑️

하지만 신경망을 이보다 더 깊이 쌓으면, 성능 저하(degradation)라는 문제점에 마주하게 됩니다.
accuracy는 포화상태에 이르고, 급격하게 감소하게 됩니다.

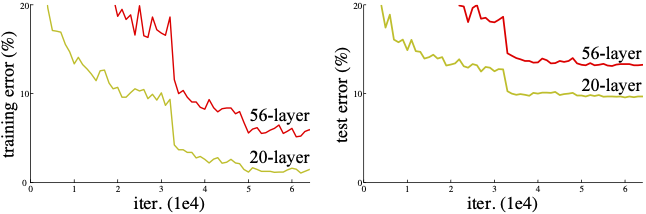
이는 과적합(overfitting)때문이 아니라, 적절히 깊은 모델에 더 많은 레이어를 추가할수록 오히려 학습 오류가 증가한다는 실험 결과로 입증되었습니다.
위 그림은 CIFAR-10 데이터셋을 단순한 20층 신경망과 56층 신경망을 비교한 실험입니다. 왼쪽은 training error이고, 오른쪽은 test error 실험입니다.
에러율이 학습단계와 검증단계 모두에서 56층 신경망에서 높은 것을 알 수 있습니다.

본 논문에서는 이러한 성능 저하 문제를 해결하기 위해 잔차 학습(residual learning) 프레임워크를 도입하였습니다.
쌓인 몇 개의 레이어가 원하는 매핑 H(x)를 직접 학습하는 residual mapping F(x) := H(x) - x를 학습하도록 설계하였습니다.이를 통해 원래 매핑은 H(x) = F(x) + x로 재구성되며, residual mapping을 학습하는 것이 원래의 복잡한 매핑을 직접 학습하는 것보다 다 최적화가 쉽다는 것을 주장합니다.

---

2. How : 연구 방법론

2.1. Residual Learning

기존의 네트워크는 stacked layers를 통해 입력 $x$에서 출력 매핑 $H(x)$를 직접 학습하였습니다.
그러나 ResNet에서는 이를 재구성하여, stacked layers가 $H(x)$ 대신 잔차 함수 (residual functions) $F(x) := H(x) -x$를 학습하도록 설계하였습니다.
원래 목표 매핑 $H(x)$는 위 식을 근거로 $F(x) + x$로 표현할 수 있습니다.
이 재구성은 층들이 더 간단한 변화를 학습할 수 있도록 하며, 학습이 더 쉬워질 수 있다는 가설을 기반으로 재구성되었습니다.

2.2. Identity Mapping by Shortcuts

$y = F(x, \{W_i\}) + x$

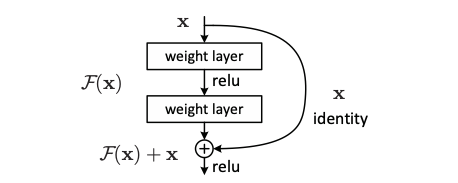
• $x$ : 입력 벡터
• $y$ : 출력 벡터
• $W_i$ : 블록의 가중치
• $F(x, \{W_i\})$ : 학습해야 할 잔차 매핑

로 위 식은 shortcut connection을 통해 input vector $x$와 residual mapping $F(x)$를 덧셈으로 결합한 학습가능한 함수로 표현한 것입니다.

위 그림은 층이 2개입니다. 식으로 표현하자면

로 표현할 수 있습니다.
참고로 $\sigma$는 ReLU를 뜻합니다.
저자가 bias는 수식에서 표기하지 않았다고 합니다.

만약 차원이 다른 경우는 shortcut connection을 수정해야 합니다.
shortcut connection에 대해서는 다음 섹션에서 설명하도록 하겠습니다.

2.3. Network Architectures

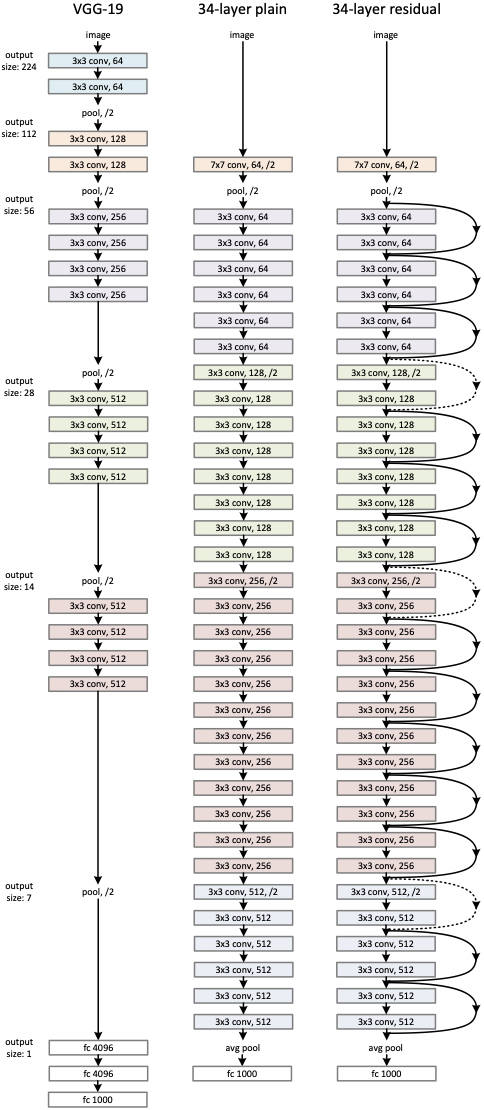
논문에서는 Plain Network와 Residual Network 두가지 모델로 실험을 진행하였습니다.

Plain Network는 VGGNet의 설계 철학에서 영감을 받아 다음과 같은 원칙으로 설계되었습니다.

• 합성곱 층은 3X3 필터를 사용한다.
• output feature map의 크기를 같게하기 위해 각 층들은 동일한 필터 수를 갖습니다.
• 만약 feature map의 크기가 절반으로 줄어든다면, 필터 수를 두 배로 늘려 층별 계산 복잡도를 일정하게 유지합니다.
• stride=2인 합성곱층을 사용하여 다운샘플링을 수행합니다.
• 마지막 층은 Global Average Pooling layer와 1000개의 클래스를 출력하는 Fully-Connected layer와 소프트맥스로 끝납니다.

Residual Network는 Plain Network를 기반으로 만들어졌습니다.

• 추가된 것은 shortcut connection을 추가하여 residual Network로 변형하였다는 것입니다.
• input과 output의 차원이 동일할 경우, identity mapping을 사용합니다.
• input과 output의 차원이 동일하지 않을 경우, 2가지 방법이 있습니다.
  1. zero-padding을 수행하여 identity mapping을 수행할 수 있도록 차원수를 증가시키고 identity mapping을 사용합니다.
  2. projection shortcut을 차원을 맞추기 위해 사용됩니다.
     projection shortcut은 $y = F(x, \{W_i\}) + W_s x$로 나타냅니다.

2.4. Implementation

Plain Network와 Residual Network 둘 다 구현 세부사항은 아래와 같습니다.

• SGD(Stochastic Gradient Descent) 사용
• learning rate : 0.1로 설정, 학습이 진행됨에 따라 점진적으로 감소
• momentum : 0.9로 설정
• weight decay : 0.0001로 설정
• mini batch : 256으로 설정
• 데이터 증강 :
  • 이미지의 가로 세로 중에 짧은 변을 256 ~ 480 사이의 값으로 다운샘플링 수행
  • 224x224크기 random crop
  • Horizontal Flip

으로 모델을 구현하였다고 합니다.

---

3. Experiments

논문의 실험 결과입니다.

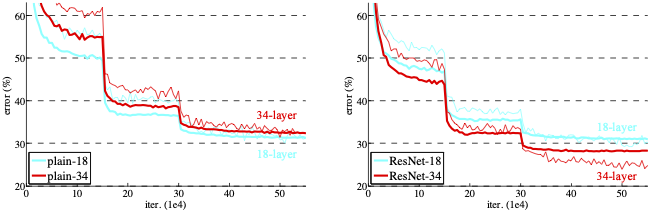
왼쪽 결과는 Plain Network 18층과 34층의 차이를 보여주는 그림입니다.
Plain Network는 층이 깊은 모델이 학습이 진행됨에 따라 error rate가 더 높음을 보여줍니다.
반면 ResNet은 층이 깊음에도 불구하고 34층 모델의 error rate가 작음을 보여줍니다.

이 결과로 Residual Block이 층을 깊게 쌓아도 degradation 문제를 발생시키지 않음을 알 수 있습니다.

---

4. Conclusion

Residual Block을 이용하여 성능 저하 없이 층을 깊게 쌓을 수 있는 방법을 보였습니다.
ResNet은 이후 컴퓨터 비전뿐 아니라 자연어 처리, 음성 인식 등 다양한 분야에서 모델 설계의 표준으로 자리 잡았으며, 딥러니의 심층화와 효율성 간의 균형을 맞추는 데 전환점을 제공했습니다.