CNN
MLP의 fully conneted layer는 가중치 행렬이 매우 크다.

반면 CNN은 kernel이라는 고정된 입력벡터를 사용한다.

- 모든 i에 대해 커널 V를 적용한다.
- 커널의 사이즈만큼 x 상에서 이동하며 적용한다.
- 활성화 함수를 제외한 convolution 연산도 선형변환이다.
수식
continous, discreate한 경우에 아래와 같이 수식이 이루어진다.
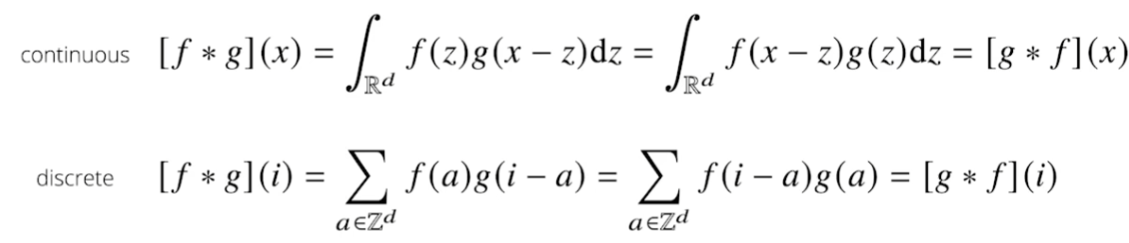
convolution 연산은 신호(signal)을 국소적으로 증폭/감소시켜 정보를 추출/필터링하는 것.
Cross-correlation
convolution 연산을 +로 엮은 것이다. 실제로 CNN을 구현할 때 cross-correlation이 사용된다. 전통적으로 cross-correlation을 convoltion으로 불렀지만, 실제로는 다른 연산이다.

convolution 연산
translation invariant : 커널은 정의역 내에서 움직여도, 커널 자체가 변하지는 않는다.
또한 커널은 신호에 국소적으로만 적용된다.


이미지에서의 convolution 예시
체험 링크 : https://setosa.io/ev/image-kernels/
다차원에서의 convolution 수식
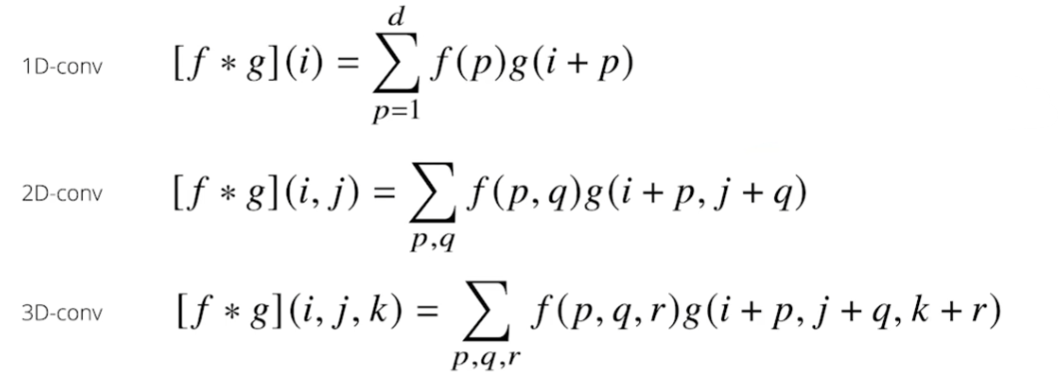
convolution 적용
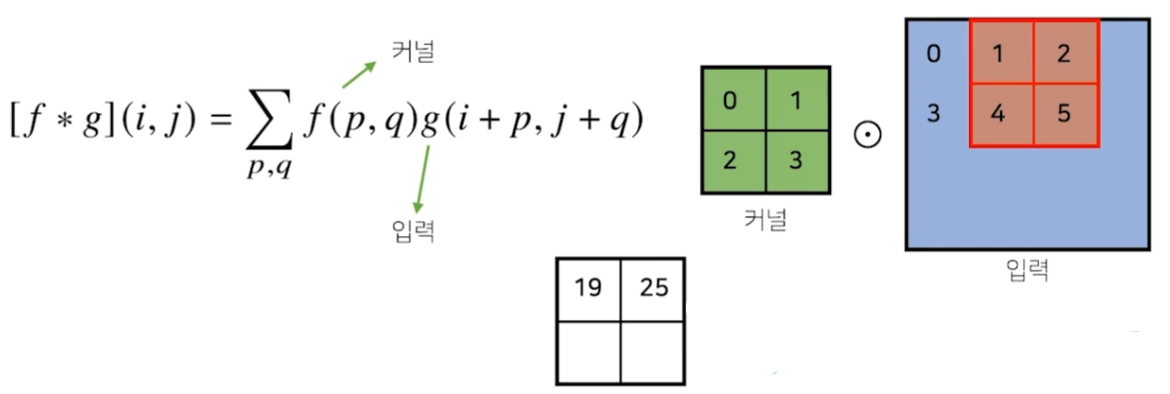
- f가 커널, g가 입력이다.
- 입력에 대한 좌표가 (i, j)
- 예시에서 p, q의 범위는 각각 0~1, 0~1이다. 즉, p, q의 범위는 커널 내의 요소와 입력 행렬의 요소를 한쌍으로 지정해주는 역할을 한다.
- 각각을 element-wise하게 곱해주고 sum한다.
- 이를 입력의 범위를 벗어나지 않는 선에서 반복한다.
convolution 크기 예상
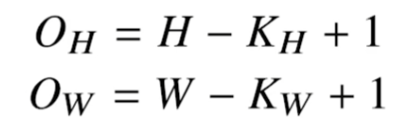
- 입력 크기 = (H, W)
- 커널 크기 = (KH, KW)
- 출력 크기 = (OH, OW)
2차원 convolution
3차원부터는 행렬이라고 하지 않고 Tensor라고 한다.
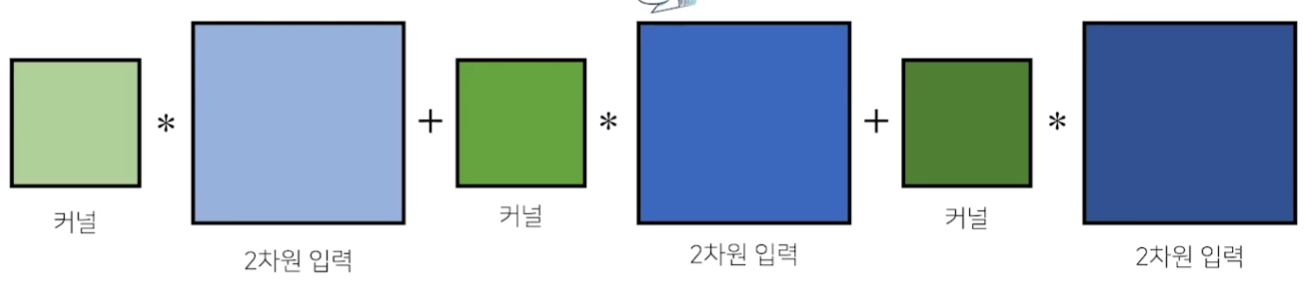
2차원 입력이 3채널로 들어올 경우 위와 같이 convolution 연산을 한다.
각각의 채널마다 커널을 생성하고, 해당 채널의 커널과 2차원 입력에 대해서 convolution 연산을 한다. 그리고 이 결과들을 모두 합한다.
이를 그림으로 설명하면 아래와 같다.
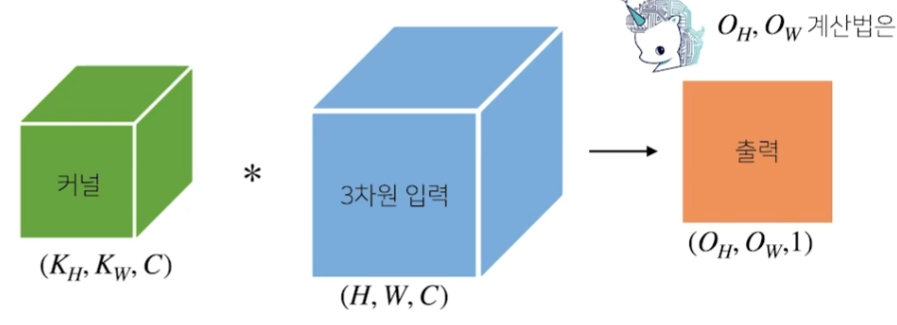
3차원 커널과 3차원 입력이 준비돼있다. 물론 2차원 입력에 대한 채널을 상정했기 때문에 3차원이 된 것이다.
이 때, 3차원과 3차원의 convolution 연산을 하면 1개 채널의 2차원 출력물이 발생한다. 모든 채널에 대해서 커널을 모두 준비했기 때문이다.
2차원 출력의 채널을 1개가 아닌 여러개로 만들고 싶다면, 3차원 커널 텐서를 여러개 만들어서 적용하면된다!

CNN의 back propagation
역전파를 계산할 때도, 똑같이 convolution 연산이 나온다. 말이 어려운데 수식으로 설명하면 아래와 같다.
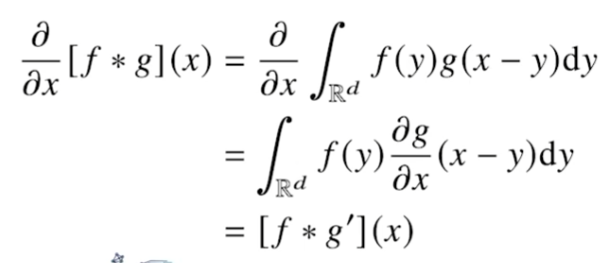
- f : 커널
- g : 시그널(입력)
- 하고자하는 것 : f와 g의 convolution 연산에 대한 미분
x에 대해 미분하고자하면 x 항은 g만 가지고 있기 때문에, 미분은 g에만 붙는다.
즉, 수식의 두번째 줄처럼 f와 g의 도함수에 대한 convolution 연산으로 변하는 것이다!!
이는 discrete에서도 똑같이 적용된다.
예시
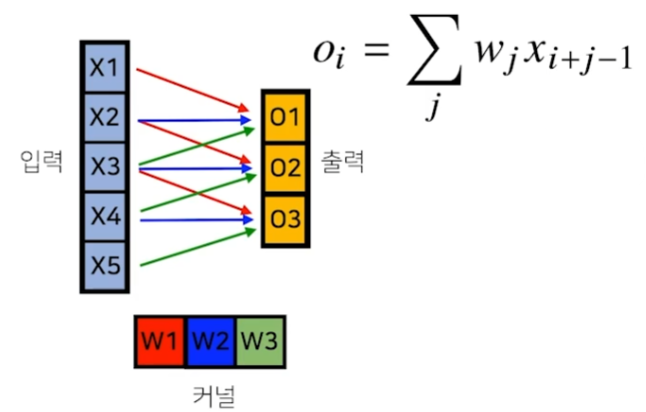
입력과 커널이 벡터인 상태에서 convolution 연산을 시행한다고 해보자. 결과들은 출력 벡터에 저장된다.
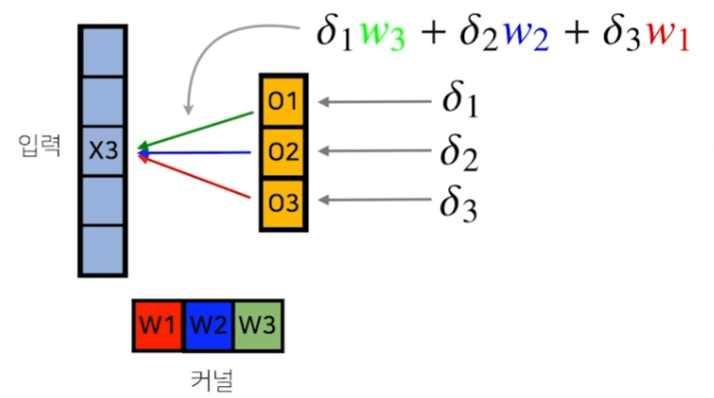
loss function에서 error값이 연산되고, 이에 대한 미분값이 역전파 단계를 통해 출력벡터까지 온 상황을 가정해보자.
헷갈리수도 있는데, 위위 그림에서 보면 X3와 W3이 곱해져서 O1에 전달됐다. 같은 원리로 X3와 W2가 곱해져서 O2, X3와 W1이 곱해져서 O3로 전달됐다.
이와 동일한 방식으로 미분값들도 커널의 W3, W2, W1과 곱해져서 X3에 전달된다.
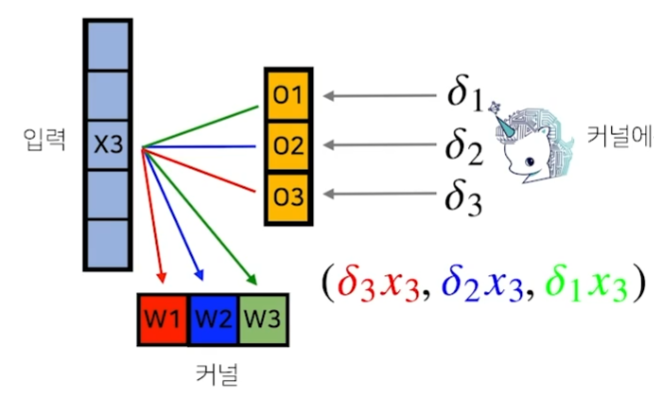
커널도 동일한 방식으로 업데이트가 된다고 한다. 사실 이부분은 잘 이해가 되지 않는다...

결국 모든 과정들을 종합해보면 back propagation조차도 convolution 연산과 동일하게 진행이 된다!
