Neural Networks

인간이 가진 뇌의 신경망을 모방했기 때문에 잘 작동한다고도 한다.

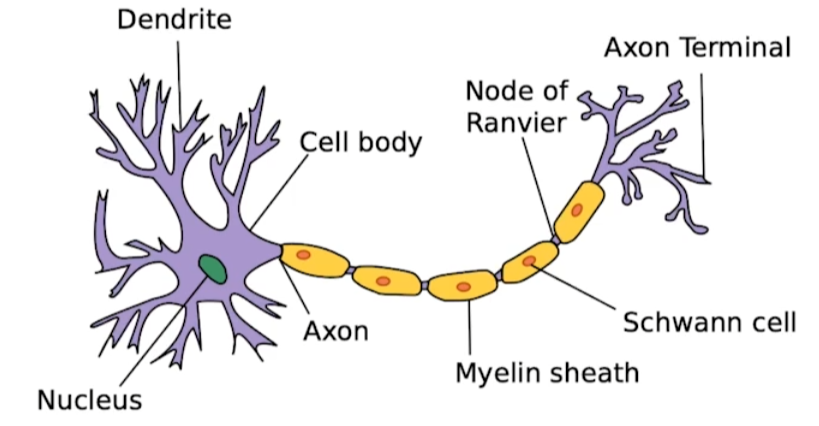
어느 정도 맞는 말이다. 실제 뉴런의 형태를 모방해서 구현된 것이 NN의 node와 흡사하다.

하지만 굳이 뇌를 모방한 것이라 하기에는 Back propagation과 같은 과정이 NN에는 필수적이다.

초창기의 비행기는 박쥐, 새를 모방했다. 라이트 형제의 비행기도 어느정도 그러한 형태이다. 하지만 최근의 비행기에서는 박쥐, 새를 모방했다고 할 수는 없다.

NN도 마찬가지이다. 인간의 지능을 모방하기 위해서 인간의 뇌를 모방하는 것에서 시작했지만, 최근의 DL 연구들은 인간의 작동방식과 매우 상이하다.

결론은 NN이 잘 작동하는 이유를 단순히 인간을 모방했기 때문이라 단정하지 말고, 수학적으로 왜 그러한지 분석해야 한다.

Define

Neural networks are function approximators that stack affine tarnsformations follwed by nonlnear transformations.

• 함수를 근사한다.
• Activation function을 통해 비선형적으로 구현.

Linear Neural Network

Simple data

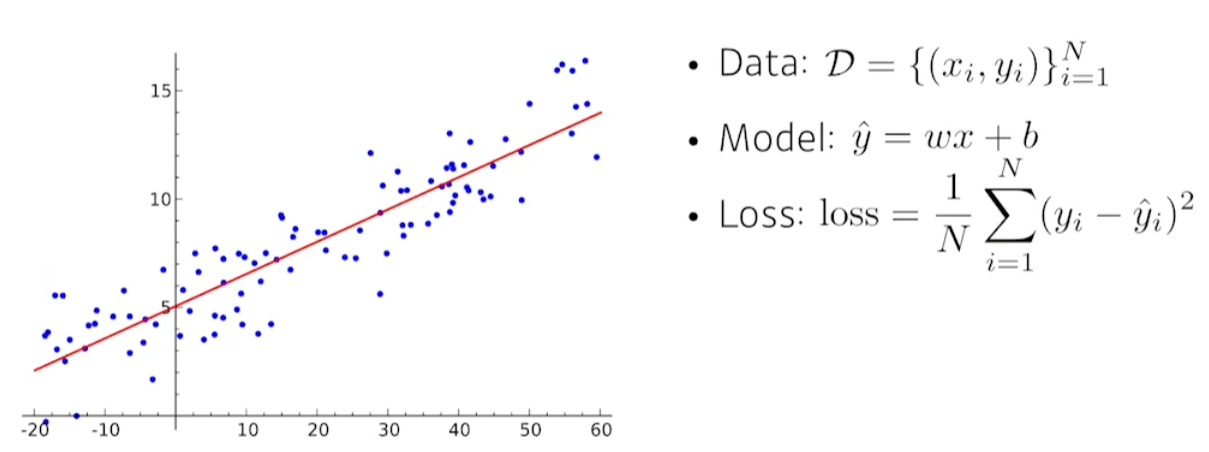
data, model, loss를 위와 같이 정의해보자.
이 때, model의 parameter인 최적의 w와 b를 찾아보자.

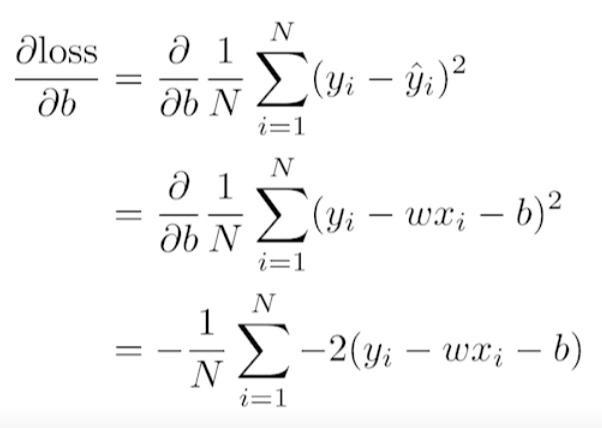
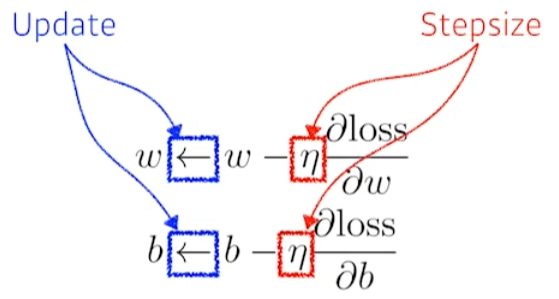
Linear regression 문제이고, convex function이고, 많이 않은 학습 데이터들이 사용됐기에 최적의 w와 b를 한번에 구하는 방법론이 분명 존재한다. 하지만 DL에서는 이를 위와 같이 back propagation을 통해 구한다.

back propagation의 목표 : loss를 최소화하는 방향으로 parameter 업데이트.
back propagation에 대해서는 다른 포스팅에서 자세히 설명했기 때문에, 더 자세하게 서술 안한다.

More large data

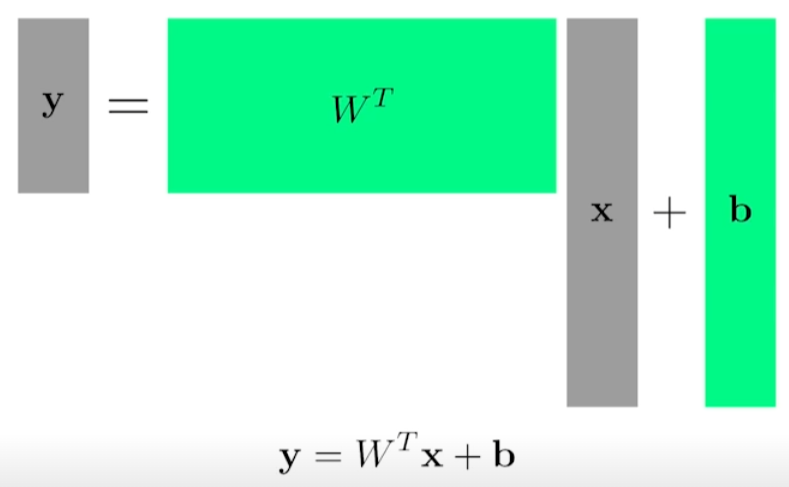
행렬을 통해 가중치들을 표현. W와 b를 통해 x를 y로 보내는 것이 목표.

More layer stack

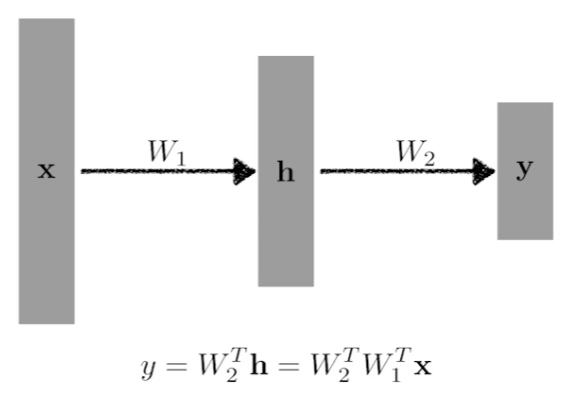
layer를 더 쌓고 싶다면 가중치의 곱으로 표현할 수 있다. 위의 형태는 앞선 기본적인 수식을 중첩시킨 것이다. (bias는 무시하고 표현)

위의 방식으로 hidden layer가 존재하는 multi layer를 의도했지만, 결론은 이 또한 하나의 layer라고 생각할 수 있다. 왜냐하면 W2와 W1이 행렬곱을 통해 하나의 가중치처럼 표현되기 때문이다.

따라서 위와 같이 Nonlinear transform을 수행한 후에, 다시 선형변환과 결합시켜야지 layer를 쌓는 효과가 발생한다.

Activation functions

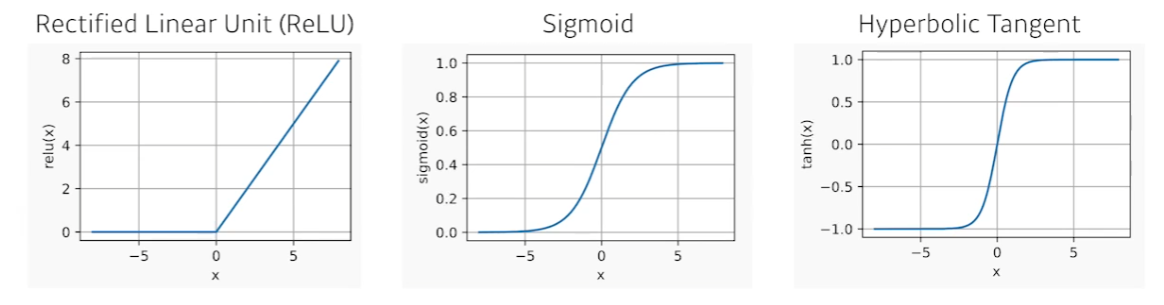
어떤 것이 좋을지는 문제마다 다르다.

Beyond Linear Neural Networks

임의의 집합 K에서 우리가 원하는 continous한 function은 한 개의 hidden layer만으로 우리가 원하는만큼 근사할 수 있다.
=> 존재성만을 암시. 즉, 내가 학습시킨 NN이 내가 원하는 함수를 근사할 것이라는 보장이 아니다.

NN의 표현력만을 보여준다.

Loss function

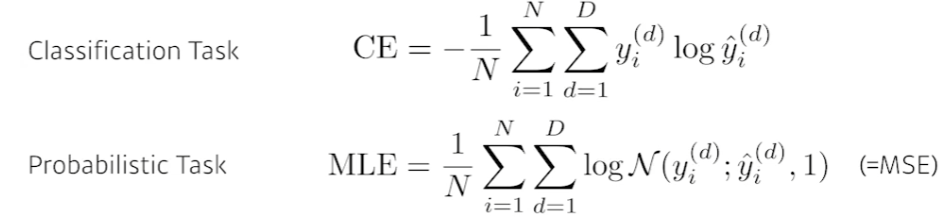
cross entropy는 분류 문제에서 사용된다.

분류 문제에서의 라벨은 보통 one-hot 벡터로 표현된다. 즉, 분류하고자 하는 차원만 값이 존재하고 나머지는 전부 0인 것이다. 이 때, 해당 값은 뭐든 상관없다. 1이어도 되고 1000000이어도 된다.
다른 값들과 다른 것으로 분류가 되기 때문이다.

이러한 특성을 수식으로 표현하기 위해 cross entropy를 사용한다고 한다.

혹은 사람의 얼굴을 보고 나이대를 추측하는 모델을 만들고자 한다. 이럴 때는 보통 확률로써 표현하게 되는데, MSE를 통해 log likelihood를 활용해 구현한다.