[컴퓨터비전] Image Filter – Convolution
Image Filter
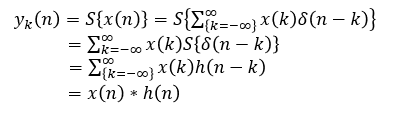
이미지 필터는 입력 이미지에 컨볼루션 연산을 적용하는 것이다
필터링된 영상은 필터 시스템의 출력값이다
Convolution

컨볼루션(합성곱)은 특정 함수(=커널)을 통해 Input image를 새로운 output image로 변화시키는 것이다
Correlation vs Convolution
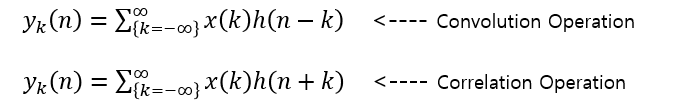
수식을 보면 부호만 다르고 나머지는 동일한 것을 확인할 수 있다
만약 커널이 대칭적이라면?

커널 h[k]가 k=0을 기준으로 symmetric하다면 h[k]=h[-k]이기 때문에 correlation과 convolution의 결과는 같을 것이다 따라서 correlation과 convolutio 연산에서 차이가 없다
non-symmetric하다면 correlation과 convolution의 결과는 다를 것이다
대부분의 image filter는 symmetric kernel로 구성되기 때문에 앞으로는 correlation과 convolution을 구분하지 않을 것이다
2D Convolution = Image Filter

공존하는 값을 더한 후 모두 더해주면 된다
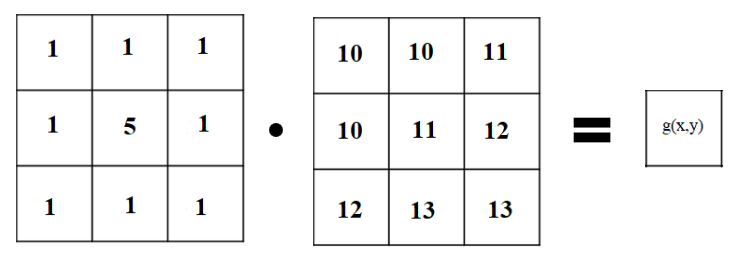
예제1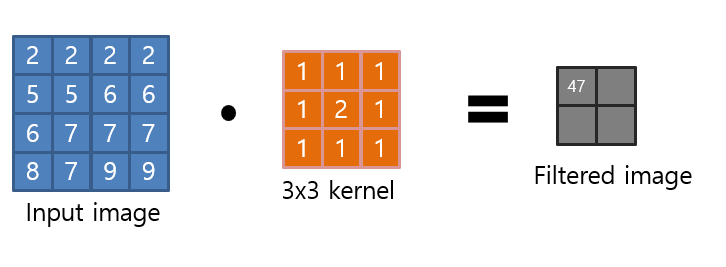
이런 경우에는
g(x,y) = 1x10 + 1x10 + 1x11 + 1x10 + 5x11 + 1x12 + 1x12 + 1x13 + 1x13 = 146
예제2
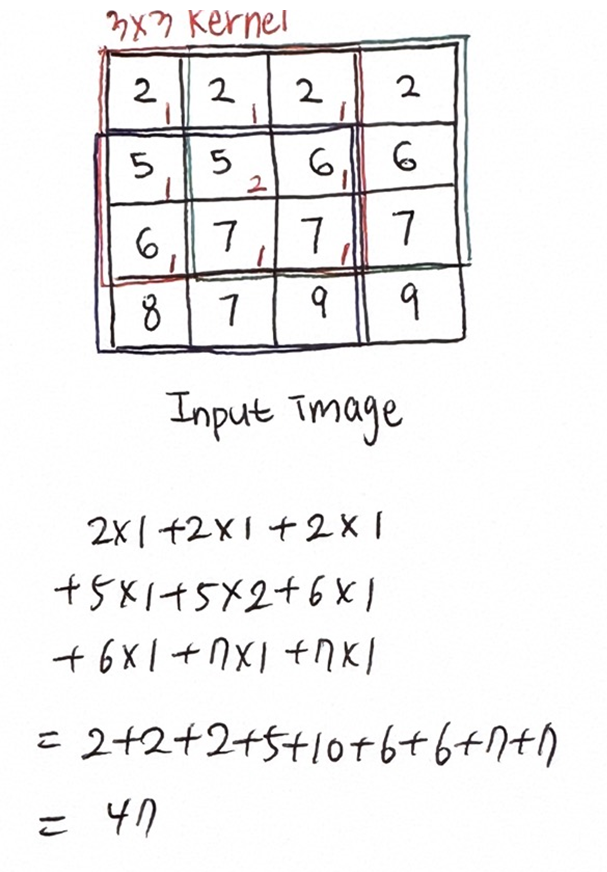
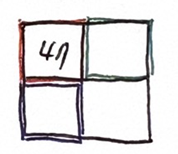
Input image에 맞게 kernel을 이동하면서 값을 구하면 된다
Convolution in Frequency Domain

frequency domain에서의 convolution은 입력함수와 응답 함수의 간단한 곱셈이다
따라서 보통 frequenct domain에서 H(f)를 구한 후 역변환해서 h[n]를 구한다
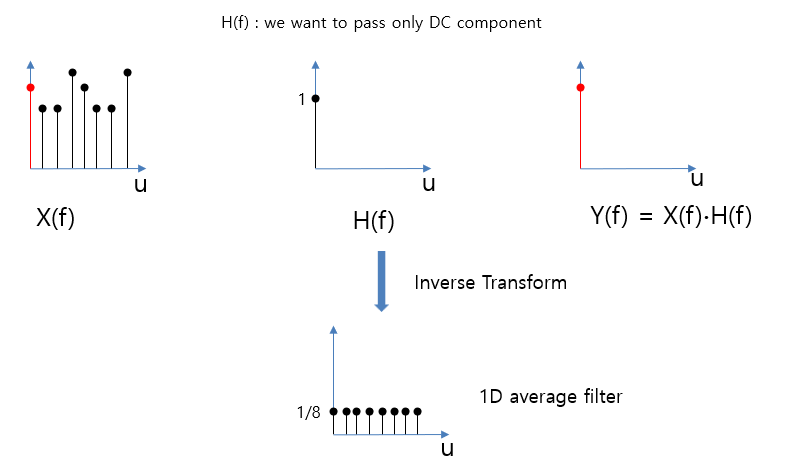
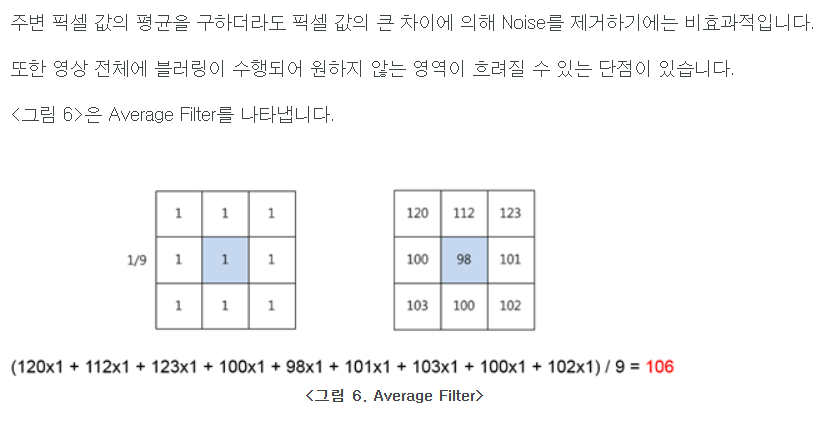
Average Filter ( or Box Filter)

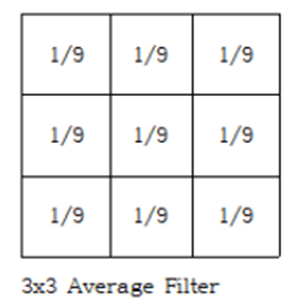
Averaging Filter는 필터의 모든 인덱스가 동일한 값을 갖는 단순한 필터이다 이미지의 부드러운 효과를 주거나 noise를 감소시키는 데 사용될 수 있다
저주파만 통과가 가능한 필터다
모든 픽셀에 대해 픽셀 값을 옆에 있는 픽셀과 동일한 수준으로 바꾼다
장점: Averaging Filter는 고주파 수 noise를 줄여준다
단점: Averaging Filter를 사용하면 이미지가 흐려진다
kernel의 크기가 클수록 더 블러리해진다
참고
https://di-bigdata-study.tistory.com/18
https://velog.io/@syiee/Computer-vision-Linear-Filters
https://velog.io/@mykirk98/AVERAGE-FILTER
https://blog.naver.com/PostView.naver?blogId=laonple&logNo=220811027599
