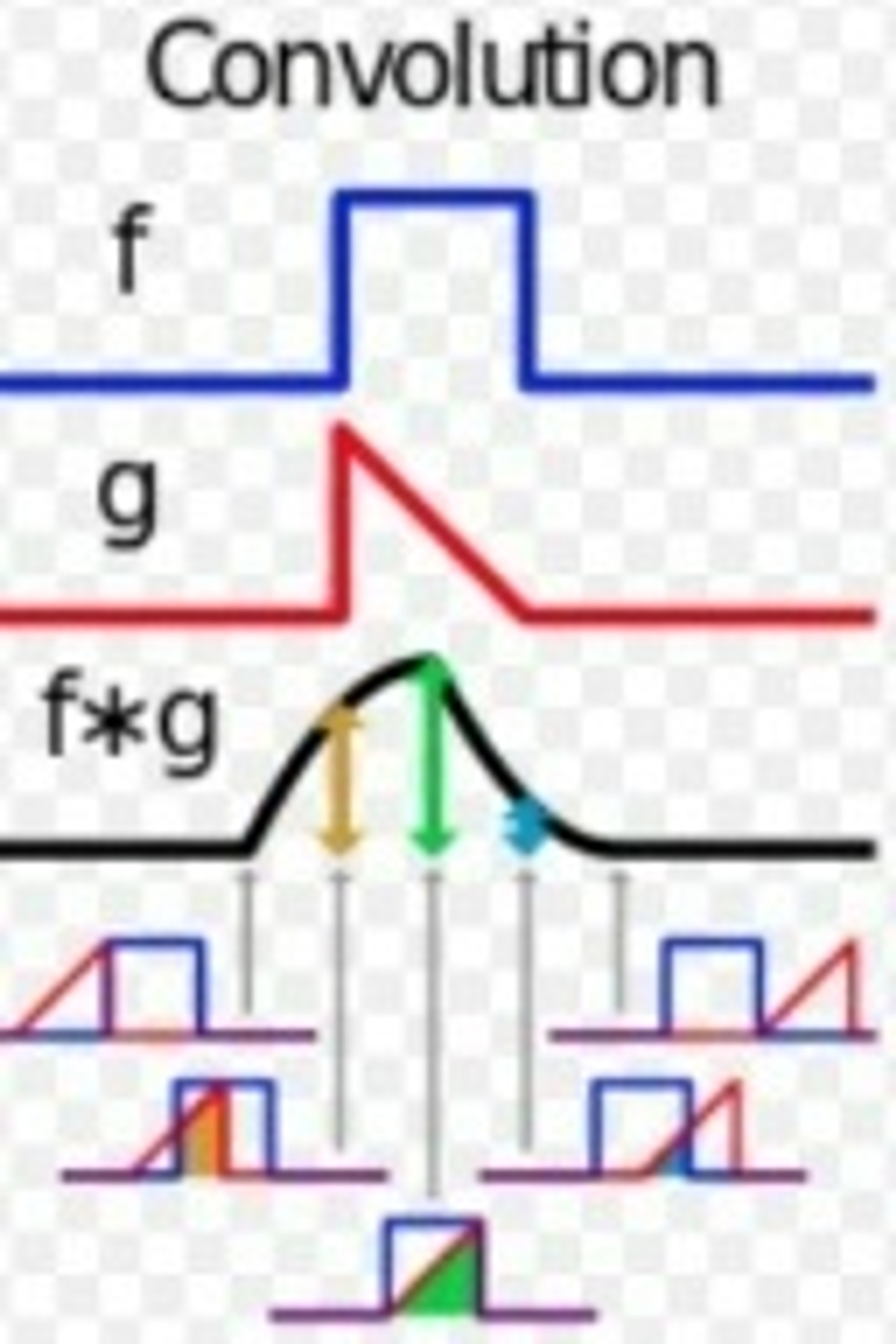
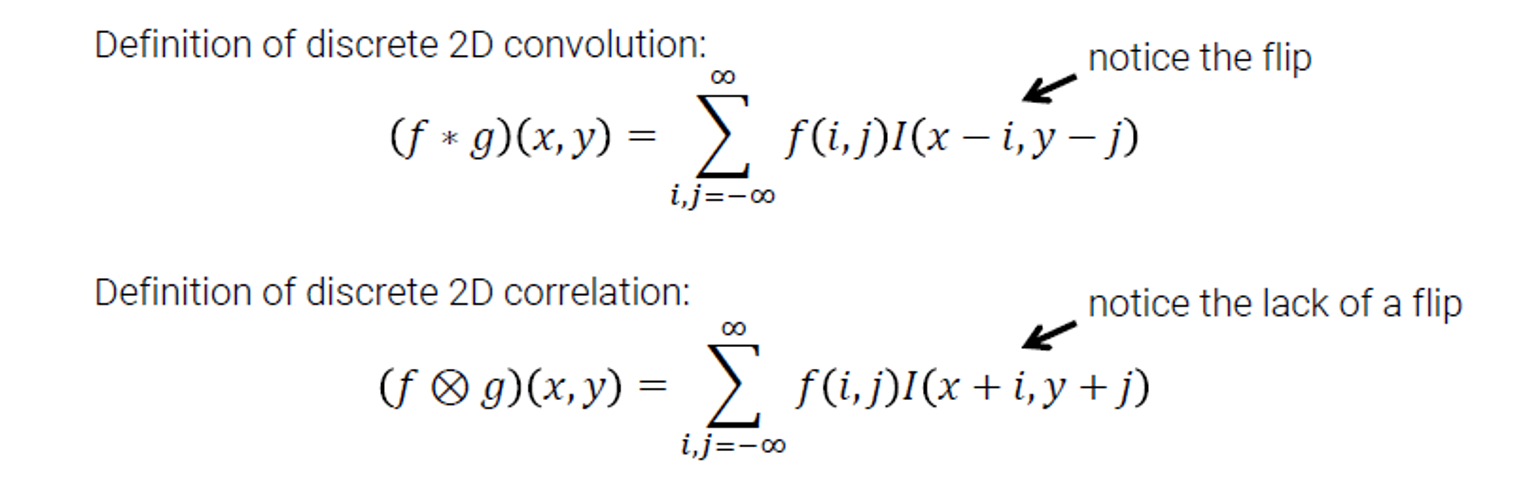📌 Linear Filters

input image weighted sum

🗨 왜 사용할까?

generality를 만들기 위해 사용한다.

💁‍♀️ 정의

Linear filter는 각각의 픽셀들을 해당하는 픽셀과 이웃한 픽셀들을 포함해서 linear combination을 이루어 값을 바꿀 수가 있다. 이때 linear combination은 filter의 kernel에 의해서 결정할 수 있으며, 이는 어떻게 만드는지에 따라서 이미지를 다양하게 바꿀 수가 있다. 모든 픽셀이 해당 픽셀과 이웃 픽셀의 동일한 linear combination을 사용하도록 동일한 kernel이 모든 픽셀 위치로 이동되게 된다.

✔ Example

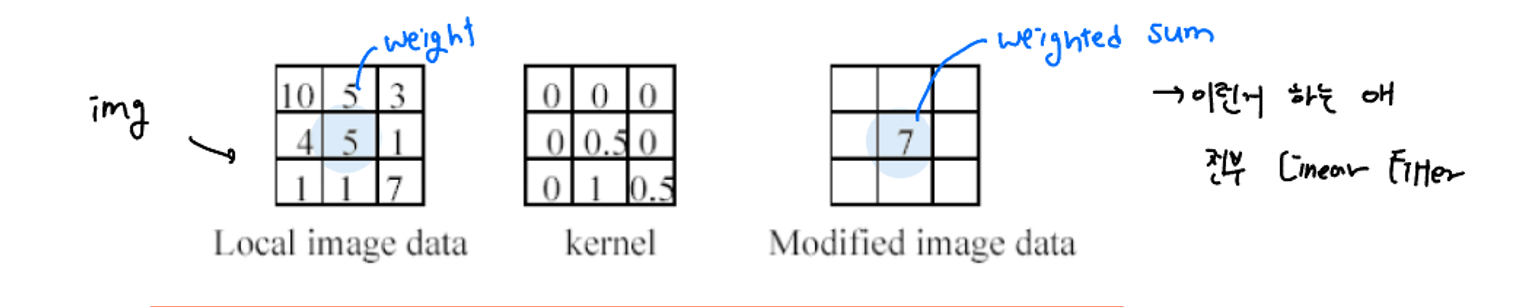
맨 왼쪽 그림은 3x3 image에서 weight를 나타내고 있다. 앞서 설명한 것 처럼 커널은 다양하게 사용이 가능한데 여기서는 가운데 사진과 같은 커널을 사용했다.

커널의 값과 image의 가중치를 곱하면 구하고자 하는 weighted sum을 구할 수 있다.

→ 50.5 + 11 + 7*0.5 = 7 ⇒ convolution kernel

이 과정은 한 픽셀에 대해 이루어진 것이다. 물론 우리는 전체 이미지에 대해 kernel을 돌릴 것이다.

그러나 처음에 gradient를 구하고 싶어서 시작하였다. 왜 convolution을 구해야 할까?

✔ Convolution (Discrete 2D)

Convolution → Linear Filter를 사용하는 것

🗨 Definition

• h(x,y) : kernel
• f(x,y) : image
• convolution h*f
  

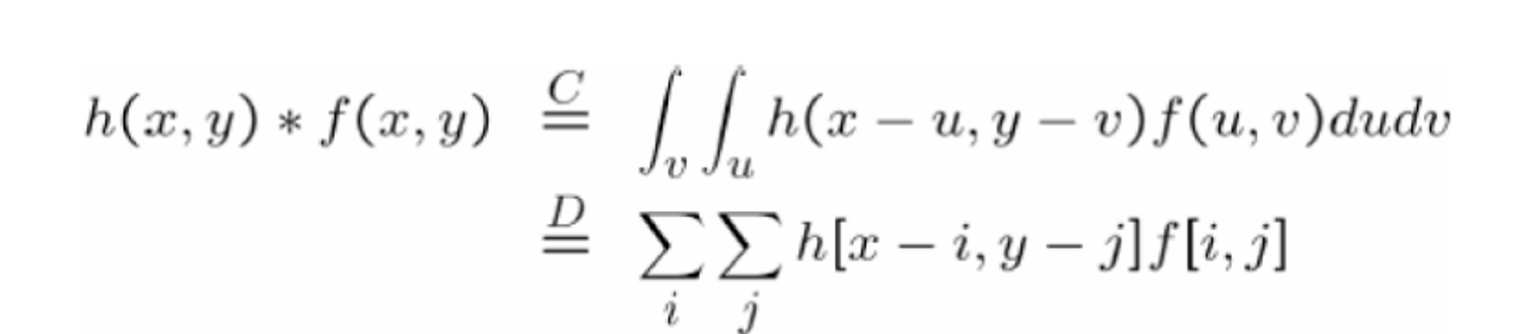
1번이 img라고 한다면 2번의 kernel을 3번처럼 뒤집고 뒤집어 img와 weighted sum을 하여 5를 구한다. → convolution

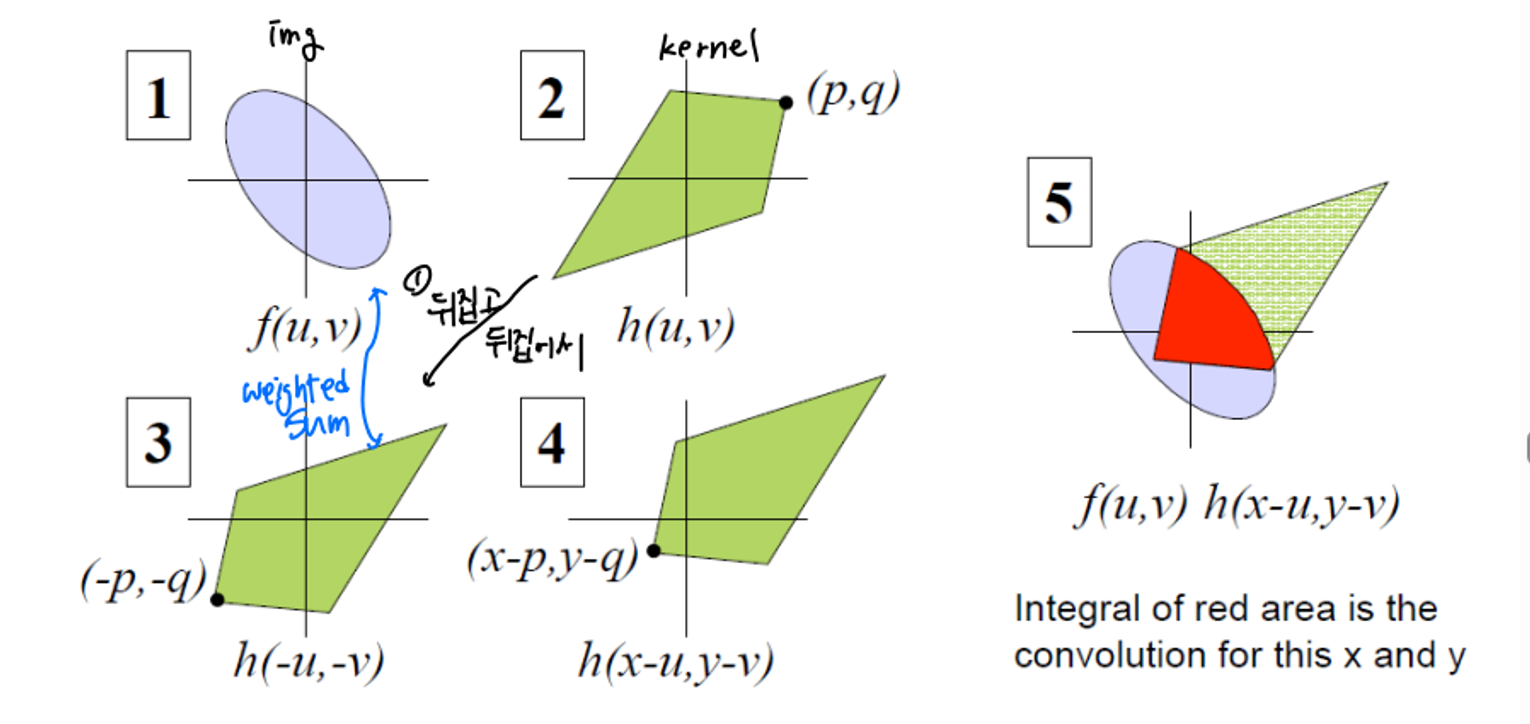
💙 More about Convolution

: 하나의 함수와 또다른 함수를 반전 이동한 값을 곱한 다음 구간에 대해 적분하여 새로운 함수를 구하는 수학 연산자

✔Properties of Convolution

Convolution is commutative.

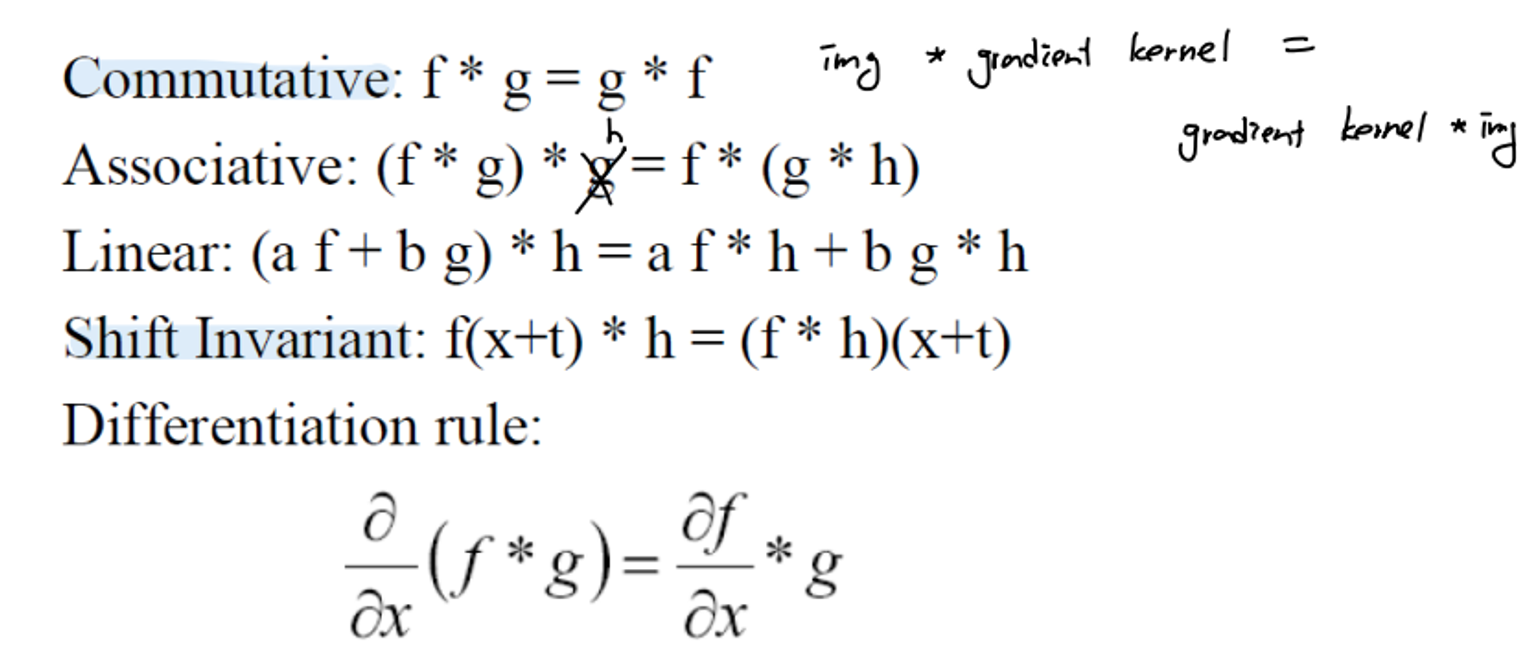
💡 Convolution vs Correlation

수식에서 부호만 다르고 나머지는 같은 것을 확인할 수 있다.

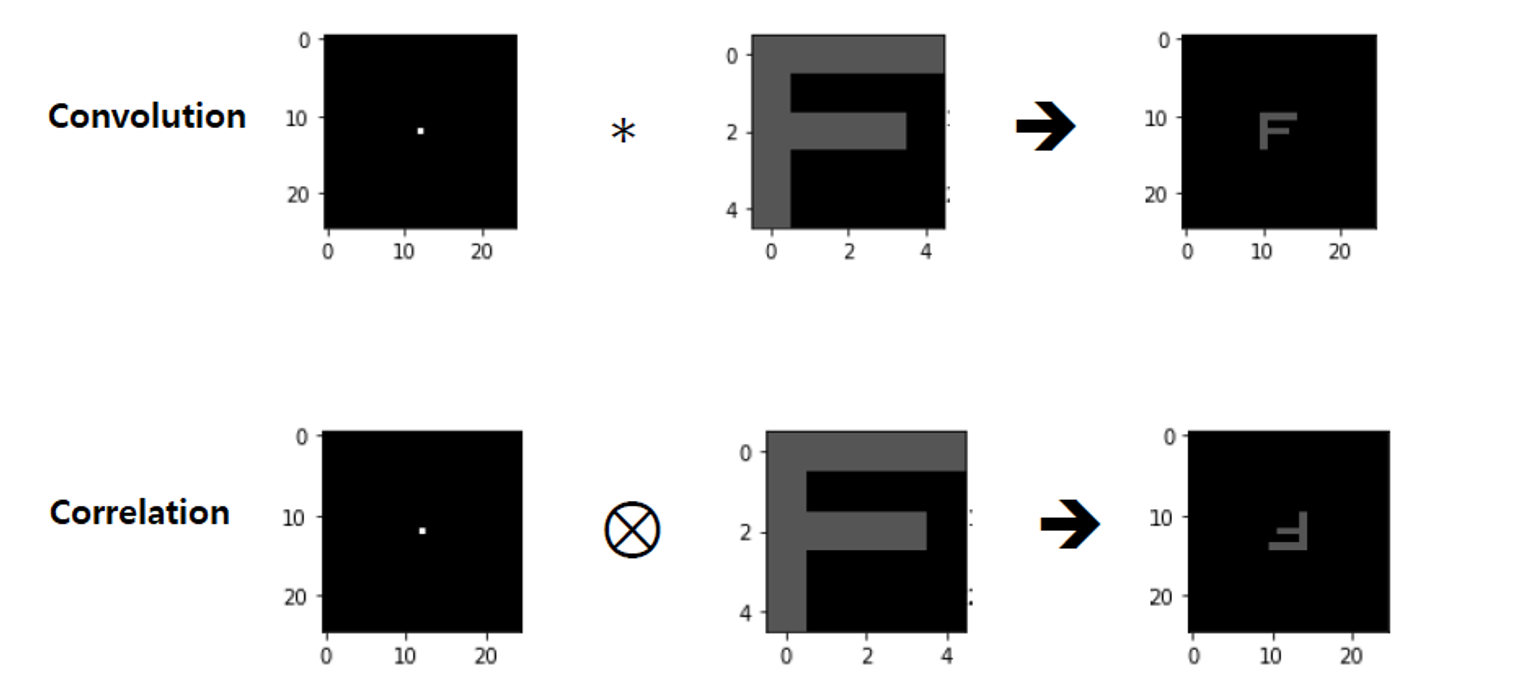
식에서 알다시피 만약에 kernel이 symmetric하다면 convolution과 correlation의 결과는 같을 것이다. 하지만 non-symmetric하다면 convolution과 correlation은 전혀 다른 결과를 가져올 것이다.

Convolution과 correlation 모두 비슷한 결과를 내는 것을 볼 수 있지만, correlation의 경우 상하좌우로 뒤집히는 것을 볼 수 있다. 이는 부호의 차이로부터 발생한 결과로 해석할 수 있다.

Convolution과 correlation의 차이는 부호밖에 없지만, 사용하는 용도와 의미는 서로 다르다.

Convolution

• 원래의 변수가 출력에도 그대로 살아있는 연산의 일종이기 때문에 그 결과가 자신이 속해있는 공간 그 자체로 보내지게 된다.
• 다른 특별한 용도를 위해서 수학적인 도구 역할이 강조

Correlation

• 원래의 변수가 다른 반수로 바뀌어 출력에 나타는 변환의 일종이기 때문에 그 결과가 자신이 속한 공간이 아닌 다른 공간에 보내지게 된다.
• 유사성의 비교 척도로 활용이 된다.

✅ Linear Filtering

= cross correlation

• 뒤집어서 사용하는 것, 업계언어로 씀
• kernel을 symmetric 하도록 제한 하면 된다.
• filter하는 것은 convolution

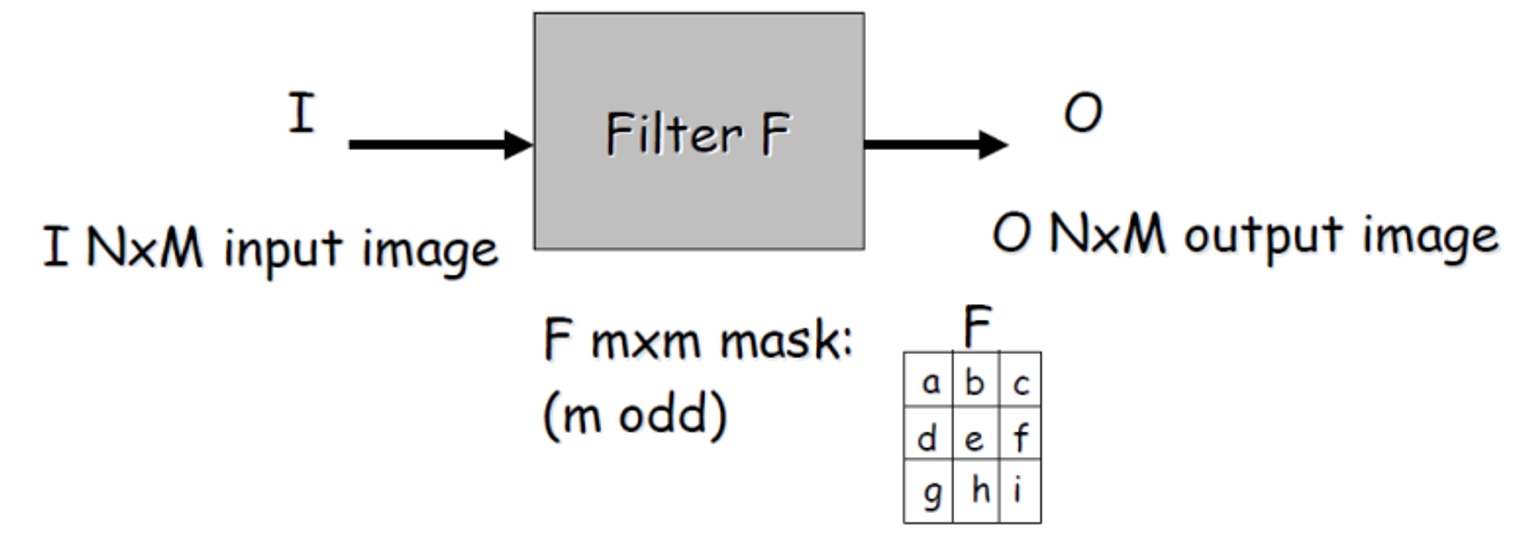
Back to the Gradient

나의 좌우 필셀 값을 이용해서 나의 gradient를 구한다.

Finite Difference Filters

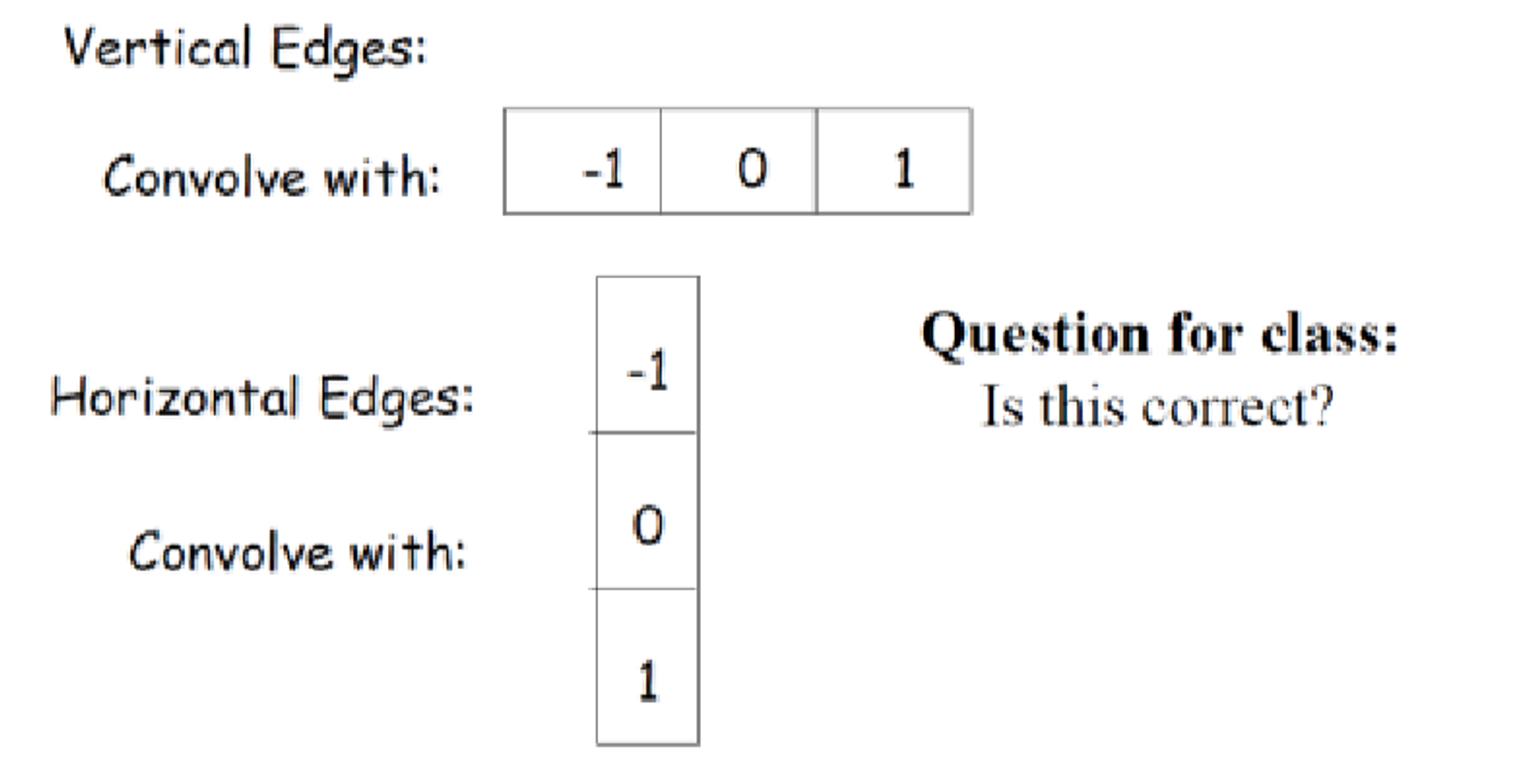
Spatial Image Gradients

우리가 이전에 gradient를 구하는 것이 사실은 convolution이었다. gradient가 미분을 통해 변화, 값의 차이를 나타내는 것이다. 그런데 [1 0 -1] 과 같은 partial derivative 필터를 통해서 convolution하면 그것이 gradient를 구하는 것과 같다는 것이다.

아래와 같이 x축, y축 커널을 다르게 사용하면 결과도 달라지는 것을 볼 수 있다

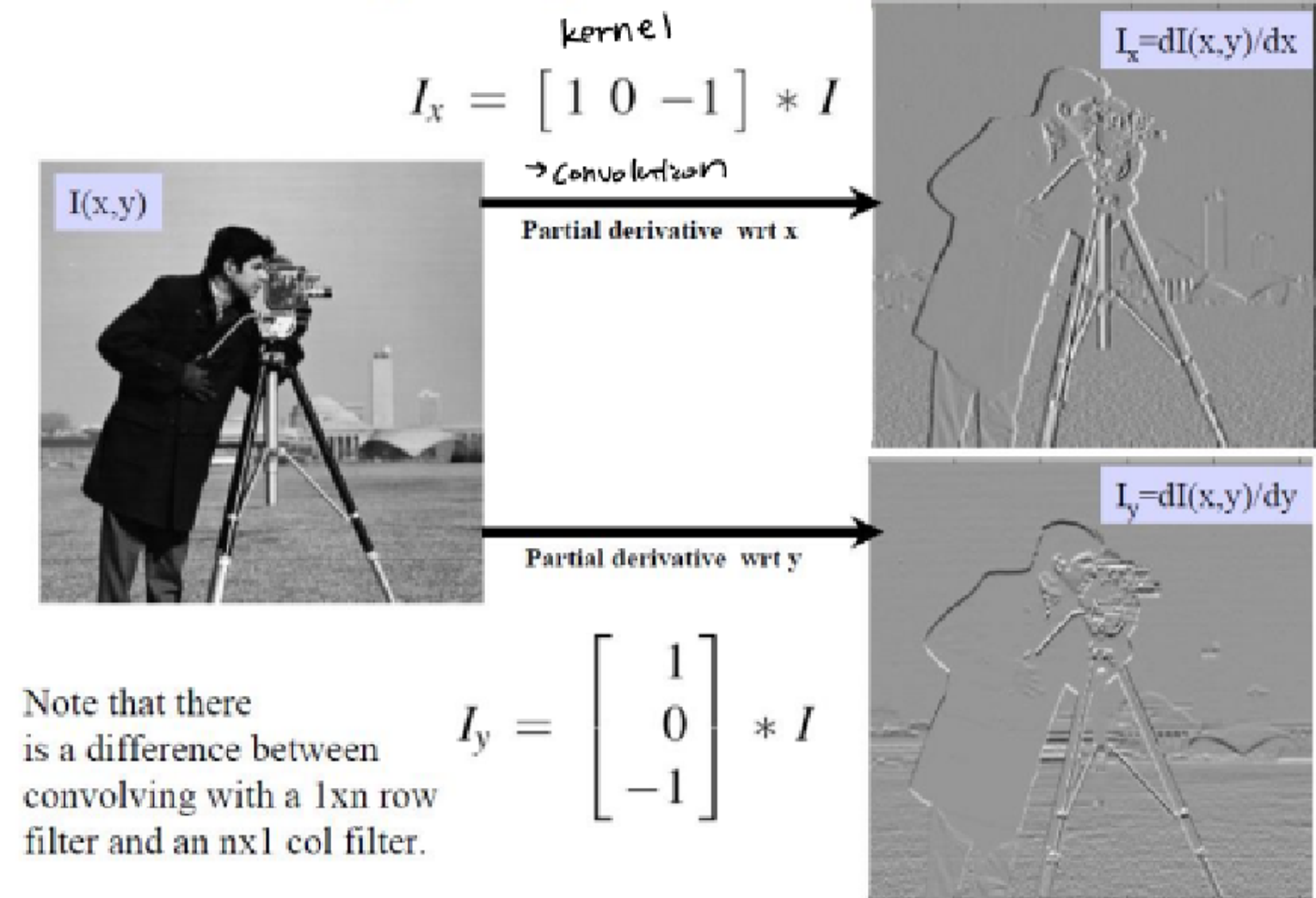
Problem : Derivatives and Noise

미분을 하면 우리가 원치 않는 값의 변화가 나온다. 이것을 Noise라고 한다. 미분의 차수가 높을수록 noise가 증폭된다.

그래서 convolution 전에는 noise를 제거해야 한다.

📌 Image Noise

• Systematic Noise : modeling 해 제거가 가능하며 rule이 존재하는 noise → 우리가 제거하고자 하는 noise
  
• Non-systematic Noise : 미리 예측이 불가능

✔ Modeling Image Noise

Simple model : just add RANDOM noise!

• $I(x,y)$ : given data
• $s(x,y)$ : what we want
• $n_i$ : noise
  → n is i.i.d(independent identical distribution)
  → zero-mean Gaussian

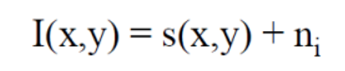
example : add Gaussian Noise

mean = 0, sigma = 16

Smoothing Reduces Noise

아래 사진과 같은 이미지 패치를 보면 균일한 색같으니 비교적 큰 변화가 없을 것 같으나 실제로 들여다 보면 안에는 굉장히 거친 표면을 갖는다.

왼쪽 사진처럼 Noisy surface를 갖는다. 그렇다면 왼쪽 사진을 어떻게 오른쪽 사진처럼 만들까? 정답은 average를 하는 것이다!

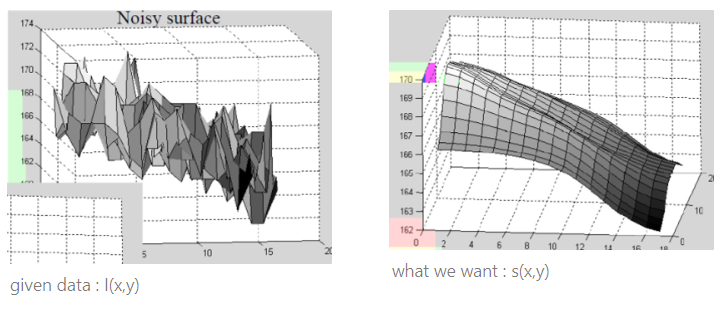
그런데 사실 왼쪽과 같은 사진이 한 장만 주어진다면 average할 수 없다. 1장이 아니라 100장을 주어야 한다. 예를 들어 위에 우리가 고른 image patch가 (7,7)에 해당한다고 가정해보자. (7,7)로 들어오는 픽셀값이 9, 9,1, 8,9, … 이렇게 데이터가 있어야 평균을 내는데 지금은 이 값이 딱 하나만 있는 상황인 것이다.

그러나, 앞서 언급한 것처럼 noise는 iid로 independent하지만 identical하니 여러 장의 사진을 받지 않아도 그냥 내 주변 값으로 할 수있다. 물론 이 방법을 사용하려면 값의 변화가 크지 않다는 가정이 있어야 한다.

따라서 위에서 고른 image patch에서는 이런 스무딩 방법을 사용해도 되지만 아래 사진처럼 급격한 변화가 있는 곳에서는 사용하면 안 된다.

Averaging / Box Filter

• 합이 1이 되어야 한다.
• 각각의 픽셀들을 그의 이웃의 값의 평균으로 한다.

Box Filter
→ 모든 weight가 같을 때

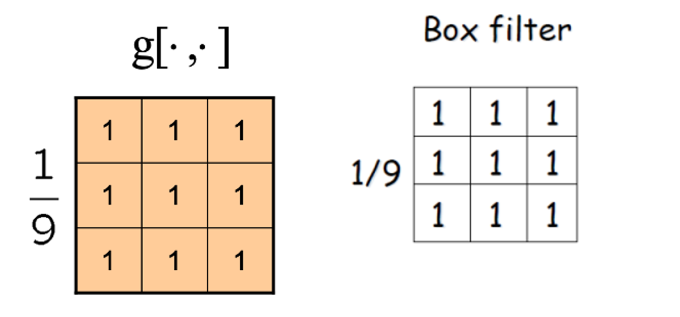
🗨 Why averaging reduces noise?

실제 식을 보면 average한 m만큼 noise가 줄어드는 것을 볼 수 있다.

smoothing with Box Filter

노이즈를 추가하는 스무딩을 통해 원치 않는 signal을 지웠는데 문제는 원하는 signal도 지워졌다.

✔ Gaussian Smoothing filter

박스 필터가 자신과 이웃을 모두 1의 똑같은 가중치로 주었다면 가우시안 필터에서는 central pixel에 더 큰 가중치를 주고 센터에서 멀어질 수록 이웃에게는 더 적은 가중치를 주었다.

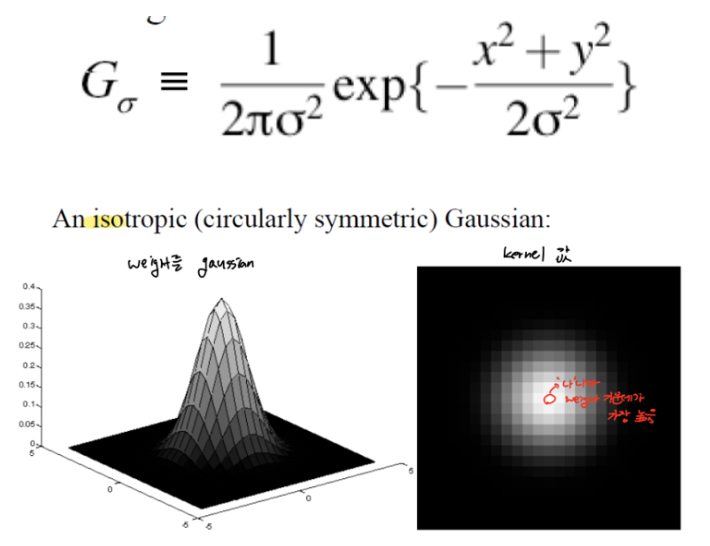
Box vs Gaussian

box filter를 사용하는 것보다 Gaussian을 사용하는 것이 조금 더 자연스럽다.

box에는 ghost line이 생긴다. ghost line은 원래 사진에는 없던 흐릿한 선들이 box filter를 통과한 후 생기는 것을 말한다.