TRAIN SHORT, TEST LONG: ATTENTION WITH LINEAR BIASES ENABLES INPUT LENGTH EXTRAPOLATION
- Github: attention_with_linear_biases
- Paper: https://ofir.io/train_short_test_long.pdf
Abstract
- 현재까지 공개된 position infomation을 주입하는 방법들이 아직 efficient extrapolation을 얻지 못했다.
- 그에따라 새로운 ALiBi(Attention with Linear Biases) 라는 방법을 제안한다
- ALiBi는 적용하기 쉽고, 효율적인 방법
- word embedding에 positional embedding 값을 추가하지 않고, query-key 어텐션 스코어에서 각 거리에따라 페널티를 주도록 어텐션 스코어를 수정한다.
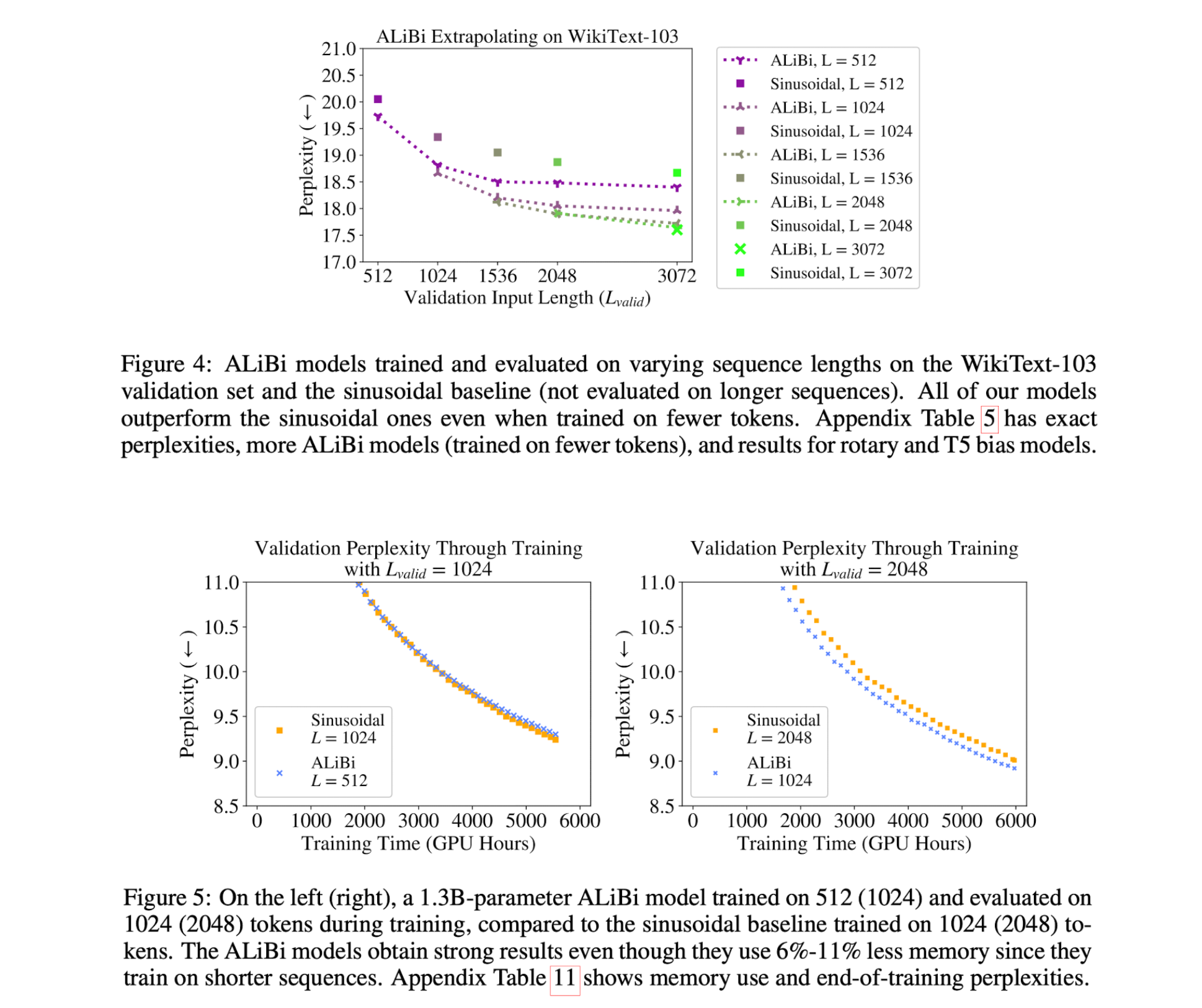
- 모델은 1.3B 모델에서 1024 학습 되고 2048 length 까지 extrapolate 한다.
- 2048 length에 대해 sinusoidal position embedding과 동일한 ppl을 얻었고, 동시에 11% 학습 효율적이고, 11% 메모리를 덜 사용한다.
- ALiBi의 inductive bias가 WikiText-103 benchmark에서 여러 position method를 뛰어넘은 경향을 보인다.
Introduction
- extrapolation: validation에서 모델이 학습한 수의 토큰들을 증가시켜서 테스트를 할때 모델이 얼마나 잘 동작하는지에 대한 능력으로 정의
- 기존에 LM에서 사용하는 sinusoidal position embedding의 경우 매우 취약한 extrapolation 능력을 가지고 있는데, 그이유는 position embedding의 한계 때문이다.
- T5 bias의 경우 기존보다는 높은 extrapolation을 가졌지만 속도가 느리고, 추가적인 메모리와 파라미터를 사용하는 단점이 있다.
- 따라서 Attention with Linear Bias(ALiBi)를 제안하며, ALiBi는 네거티브한 바이어스를 어텐션 스코어에 추가하는 방법으로 쉽고 간편하게 적용할수 있다.
- query와 key 사이의 거리에 따라 비율로 선형으로 페널티를 주는 방법을 사용.
- ALiBi는 Transformer 코드에 몇 줄을 추가 함으로써 적용할 수 있다.

Related work
Sinusoidal Position Embeddings
- Transformer 최초 모델에서 사용한 position embeddings. 학습되는 파라미터 없이 고정된 값을 사용하여 트랜스 포머의 첫 레이어에 더해준다.
Rotary Position Embedding
- GPT-J에서 공개되어 유명해진 position embedding. rotary method를 사용해 매 레이어마다 포지션 값을 주입한다.
T5 Bias
- T5에서 제안된 position embedding. attention value를 계산할때 값을 수정하는 방법을 사용. 성능 향상은 있지만 학습시간이 오래걸리고 추가적인 메모리,계산 비용이 필요하고, efficient transformer들에 적용할수 없다.
ALiBi
Notation
- : input subsequence
- 어텐션 레이어에서 어텐션 스코어를 계산할때 다음과 같이 표현할 수 있다:
-
각 헤드에서 번째 query
-
각 헤드에서 번째 key , 는 head dimension
-
Explain
ALiBI를 사용할때, position embedding 값을 추가하지 않고, query-key dot product 후에 ALiBi를 적용한다. 이때 적용되는 방법은 static하고 non-learned bias를 추가한다:
이때 은 트레이닝 전에 head specific slope 값이 고정되어 사용된다. (figure3 참고)

논문에서 사용한 8개의 헤드를 사용한 모델에서 geometric sequence를 slope에 사용했다:
16개의 헤드를 사용한 모델에서는 geometrically averaging 을 사용해 8 slope에 보간을 적용했다.
개의 헤드를 사용하는 모델에서는 으로 시작해서 geometric sequence로 slope를 구성할수 있다.
이렇게 구한 slope는 여러 도메인, 여러 모델사이즈에서 다양하게 적용할수 있으며 저자들은 새로운 데이터, 새로운 모델에 따라 slope를 구할 때 튜닝이 필요하지 않다고 믿는다.
그 이유는 저자들이 시작과 끝 위치에 따라 한번 계산되면 고정으로 사용하는 sinusoidal approach와 유사하게 method를 만들었기 때문에 모델이나 데이터의 변경에 따라 튜닝할 필요성이 없다.
ALiBi는 T5 bias와 RoPE와 같이 relative postion method로 포지션 정보를 매 레이어에 values를 제외한 keys, queries에 더해진다.
Implementation
ALiBi는 코드에서 몇줄 추가해서 쉽게 적용할 수 있다. 저자들의 구현에서는 mask matrix에 linear biases에 더해서 mask matrix를 추가한다(실제 구현에서는 transformer LM 을 학습할때, query 는 key들의 1부터 까지 어텐션을 하고 mask matrix를 softmax 연산 전에 query-key dot product 결과에 더해준다.) 이렇게 구현하는 경우 추가적인 네트워크 연산이 없기 때문에 런타임에서 효율적으로 동작한다.
sinusoidal model과 동일한 input length로 비교했을때 ALiBi는 최대 100MB 메모리를 추가적으로 사용하는 현상을 볼수 있고, 수정되지 않은 트랜스포머에서 크기의 마스크를 사용하는 경우 ALiBi에서 사용하는 마스크의 경우 를 사용하고, 만큼 더 크다. 이때 은 어텐션 헤드의 갯수 이다.
ALiBi의 마스크가 더 많은 메모리를 사용하는 이유는 linear biases각 head에 더해질때 서로 다른 를 사용하기 때문이다. 그럼에도 불구하고 ALiBi의 장점은 훨씬 더 작은 시퀀스에서도 학습할수있고, 더 긴시퀀스에서는 좋은 성능을 가지면 GB 단위의 메모리를 절약할수 있다.
구현 방법
-
Model에서 position embedding 제거
#if positions is not None: # x += positions -
Relative bias matrix set up
def get_slopes(n): def get_slopes_power_of_2(n): start = (2**(-2**-(math.log2(n)-3))) ratio = start return [start*ratio**i for i in range(n)] if math.log2(n).is_integer(): return get_slopes_power_of_2(n) #In the paper, we only train models that have 2^a heads for some a. This function has else: #some good properties that only occur when the input is a power of 2. To maintain that even closest_power_of_2 = 2**math.floor(math.log2(n)) #when the number of heads is not a power of 2, we use this workaround. return get_slopes_power_of_2(closest_power_of_2) + get_slopes(2*closest_power_of_2)[0::2][:n-closest_power_of_2] -
각 attention score를 계산하는 부분에서 mask에 bias matrix를 추가한다.
def buffered_future_mask(self, tensor): dim = tensor.size(1) # self._future_mask.device != tensor.device is not working in TorchScript. This is a workaround. if ( self._future_mask.size(0) == 0 or (not self._future_mask.device == tensor.device) or self._future_mask.size(1) < self.args.tokens_per_sample ): self._future_mask = torch.triu( utils.fill_with_neg_inf(torch.zeros([self.args.tokens_per_sample, self.args.tokens_per_sample])), 1 ) self._future_mask = self._future_mask.unsqueeze(0) + self.alibi self._future_mask = self._future_mask.to(tensor) return self._future_mask[:tensor.shape[0]*self.args.decoder_attention_heads, :dim, :dim] -
(Optional) layer loop 전으로 mask computation을 이동시키면 트랜스포머가 조금 더 빨라진다.
#We move the mask construction here because its slightly more efficient. if incremental_state is None and not full_context_alignment: self_attn_mask = self.buffered_future_mask(x) else: self_attn_mask = None # B x T x C -> T x B x C x = x.transpose(0, 1) self_attn_padding_mask: Optional[Tensor] = None if self.cross_self_attention or prev_output_tokens.eq(self.padding_idx).any(): self_attn_padding_mask = prev_output_tokens.eq(self.padding_idx) # decoder layers attn: Optional[Tensor] = None inner_states: List[Optional[Tensor]] = [x] for idx, layer in enumerate(self.layers): x, layer_attn, _ = layer( x, enc, padding_mask, incremental_state, self_attn_mask=self_attn_mask, self_attn_padding_mask=self_attn_padding_mask, need_attn=bool((idx == alignment_layer)), need_head_weights=bool((idx == alignment_layer)), ) inner_states.append(x) if layer_attn is not None and idx == alignment_layer: attn = layer_attn.float().to(x)
구현체
- lucidrain/x-transformer implementaion
Class
class AlibiPositionalBias(nn.Module): def __init__(self, heads, **kwargs): super().__init__() self.heads = heads slopes = torch.Tensor(self._get_slopes(heads)) slopes = rearrange(slopes, 'h -> h 1 1') self.register_buffer('slopes', slopes, persistent = False) self.register_buffer('bias', None, persistent = False) def get_bias(self, i, j, device): i_arange = torch.arange(i, device = device) j_arange = torch.arange(j, device = device) bias = -torch.abs(rearrange(j_arange, 'j -> 1 1 j') - rearrange(i_arange, 'i -> 1 i 1')) return bias @staticmethod def _get_slopes(heads): def get_slopes_power_of_2(n): start = (2**(-2**-(math.log2(n)-3))) ratio = start return [start*ratio**i for i in range(n)] if math.log2(heads).is_integer(): return get_slopes_power_of_2(heads) closest_power_of_2 = 2 ** math.floor(math.log2(heads)) return get_slopes_power_of_2(closest_power_of_2) + get_slopes_power_of_2(2 * closest_power_of_2)[0::2][:heads-closest_power_of_2] def forward(self, qk_dots): h, i, j, device = *qk_dots.shape[-3:], qk_dots.device if exists(self.bias) and self.bias.shape[-1] >= j: return qk_dots + self.bias[..., :i, :j] bias = self.get_bias(i, j, device) bias = bias * self.slopes num_heads_unalibied = h - bias.shape[0] bias = F.pad(bias, (0, 0, 0, 0, 0, num_heads_unalibied)) self.register_buffer('bias', bias, persistent=False) return qk_dots + self.biasInitialization
self.rel_pos = AlibiPositionalBias(heads=alibi_num_heads) - eleutherai/gpt-neox implementaion
class
class AliBi(torch.nn.Module): def __init__(self, num_heads, mp_size=1, mp_rank=1): super().__init__() # megatron splits across heads, so we need to make sure each # head receives the correct matrix assert mp_size <= num_heads and mp_rank <= mp_size self.mp_size = mp_size self.mp_rank = mp_rank self.num_heads = num_heads self.slice_size = num_heads // mp_size self.cached_matrix = None self.cached_seq_len = None slopes = torch.Tensor(self._get_slopes(num_heads))[ mp_rank * self.slice_size : (mp_rank + 1) * self.slice_size ] self.register_buffer("slopes", slopes) def _get_slopes(self, n): """ Get slopes for Alibi positional embedding n : int = number of heads. For best performance, restrict n to a power of 2. """ def get_slopes_power_of_2(n): start = 2 ** (-(2 ** -(math.log2(n) - 3))) ratio = start return [start * ratio ** i for i in range(n)] if math.log2(n).is_integer(): return get_slopes_power_of_2(n) else: closest_power_of_2 = 2 ** math.floor(math.log2(n)) return ( get_slopes_power_of_2(closest_power_of_2) + self._get_slopes(2 * closest_power_of_2)[0::2][ : n - closest_power_of_2 ] ) def forward(self, x): # [b, np, sq, sk] seq_len_q = x.shape[-2] seq_len_k = x.shape[-1] if self.cached_seq_len != seq_len_k: a = -torch.tril( torch.arange(seq_len_k).view(seq_len_k, 1).repeat(1, seq_len_k) + torch.arange(0, -seq_len_k, -1) ) a = a.to(x.device).to(x.dtype) slopes = self.slopes.to(a.device).to(a.dtype) a = a * slopes.view(self.slopes.shape[0], 1, 1) self.cached_seq_len = seq_len_k self.cached_matrix = a else: a = self.cached_matrix if seq_len_q != seq_len_k: # In the train case x has dimensionality [b, np, sq, sk] with sq == sk # The number of query tokens is equal to the number of key tokens # At inference time with cache in layer_past sq is not equal to sk. sq only contains one token (the last one in the full sequence) # In this case we use the appropriate token index of the cache matrix. # As the cache matrix could already be bigger from a past inference, not the last token index in the sq sequence is used assert ( seq_len_q == 1 ), "assumption sq == sk unless at inference time with cache in layer_past with sq == 1" a = a[:, seq_len_k - 1, :].view( a.shape[0], 1, a.shape[2] ) # seq_len_k - 1 points to the last token index in the current inference batch. return x + a
Result