Git
>>> git diff # 파일 수정 before / after 확인 가능
>>> git commit -am 'message' # -a : auto adding, tracked 상태의 파일에 대해서만
# add가 한번이라도 되었으면 tracked
>>> git add # 의미 3가지
# 1. Commit 대기 상태로 만듦
# 2. untracked를 tracked로 만듦
# 3. 충돌을 해결했다는 것을 git에게 알려줌
>>> touch .gitignore # untracked할 파일 명을 입력
# 추가된 파일은 git status에 나타나지 않는다.
>>> git reset # head가 가리키는 branch를 옮긴다.
# 마지막 작업 버전을 바꿈
>>> git remote add origin 주소 # 깃 원격 저장소 연결
>>> git merge --no-ff 브랜치 # fastfoward merge가 아닌 mergeNLP
- Seq2Seq
- it takes a sequence of words as input and gives a sequence of words as output
- it composed of an encoder and a decoder
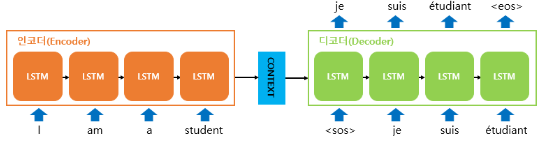
- Encoder를 지나며 생성된 이 Decoder에 들어감
- Seq2Seq with attention
- Decoder의 첫 hidden state vector인 은 Encoder을 통해 얻고 이와 각 Encoder vector의 내적을 통해 Attention scores를 얻는다. 이후 Softmax연산을 통해 Attention distribution을 만들고 이를 통해 Attention output을 얻는다.
- 그 후 Decoder의 는 (input data)와 를 통해 얻는다.
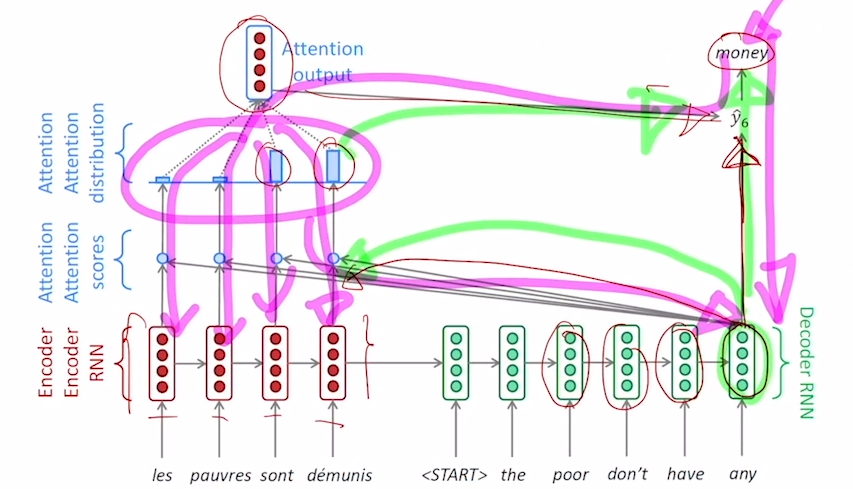
- Attention Score
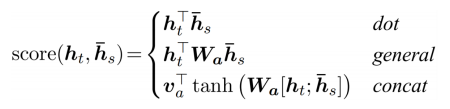
- general
- concat
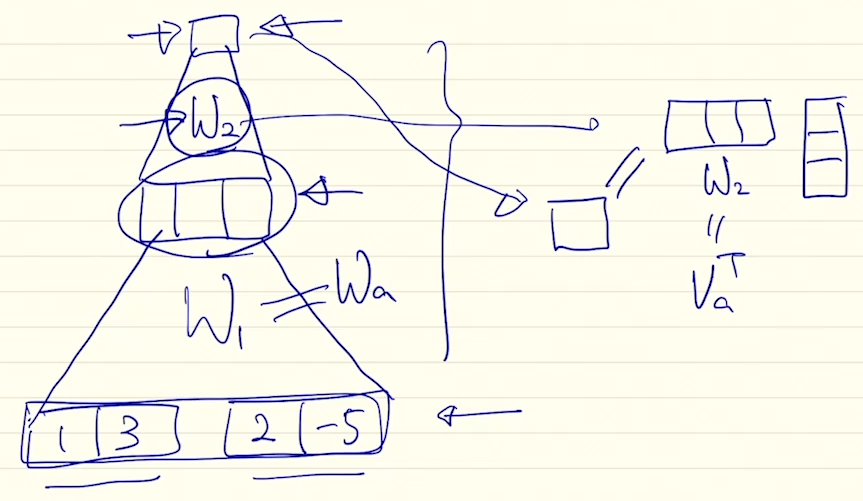
- general
-
Attention의 장점
- Attention significantly improves NMT(기계번역) perfomance
- It is useful to allow the decoder to focus on particular parts of the source
- Attention solves the bottlenect problem (Encoder의 )
- Attention allows the decoder to look directly at source; bypass the bottleneck
- Attention helps with vanishing gradient problem
- Provides a shortcut to far-away states
- shortcut이 없다면 Decoder의 time step과 Encoder의 time step을 거슬러 올라가야 원하는 곳으로 다다를 수 있다.
- Attention provides some interpretability
- By inspecting attention distribution, we can see what the decoder was focusing on
- The network just learned alignment by itself
- Attention significantly improves NMT(기계번역) perfomance
-
beam-search
- Greedy decoding은 틀린 답을 생성시 뒤로 돌아갈 수 없다.
- 그렇기에 이를 해결하기 위해 translation 를 최대화하는 lenth 를 찾기 위해 모든 경우의 수를 계산할 수 있다. (exhaustive search)
- : vocab size, step 일 때 complexity는 로 매우 높다
- Beam Search의 Core idea는 매 time step, k개의 most probable partial translations(hypothese)를 추적한다.
- not guaranteed to find a globally optimal solution
- much more efficient than exhaustive search
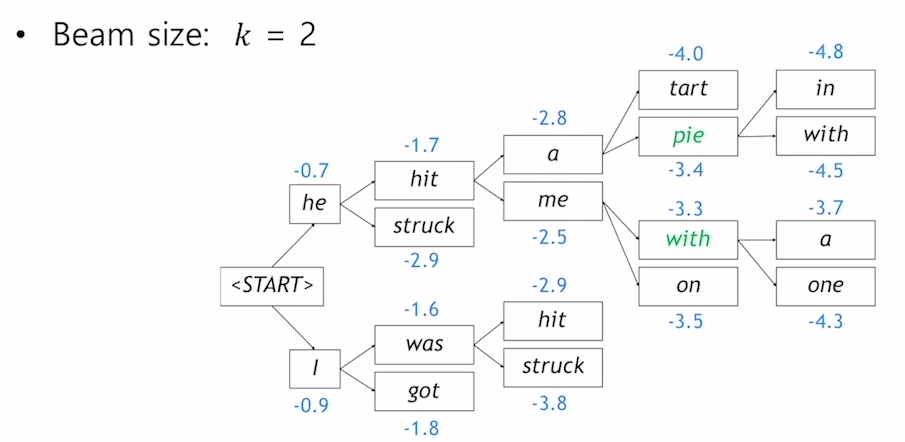
- Greedy Decoding에서 END token이 나올 때 까지 디코딩했다면 Beam search decoding에서는 diffrent timesteps에서 END token을 생성할 때 까지 디코딩한다.
- Problem with this : longer hypothese have lower scores(-log값을 더하므로)
- Fix : Normalize by length (hypothese의 길이만큼 나눠 평균을 취한다.)
-
BLEU score
- Precision =
- recall =
- F-measure =
- Precision and Recall : no penalty for reordering

- 기하 평균
- reference 길이보다 짧은 prediction을 생성할 경우 min 연산으로 인해 작은 값이 들어가 짧은 prediction에 대한 penalty를 부여 (brevity penalty)
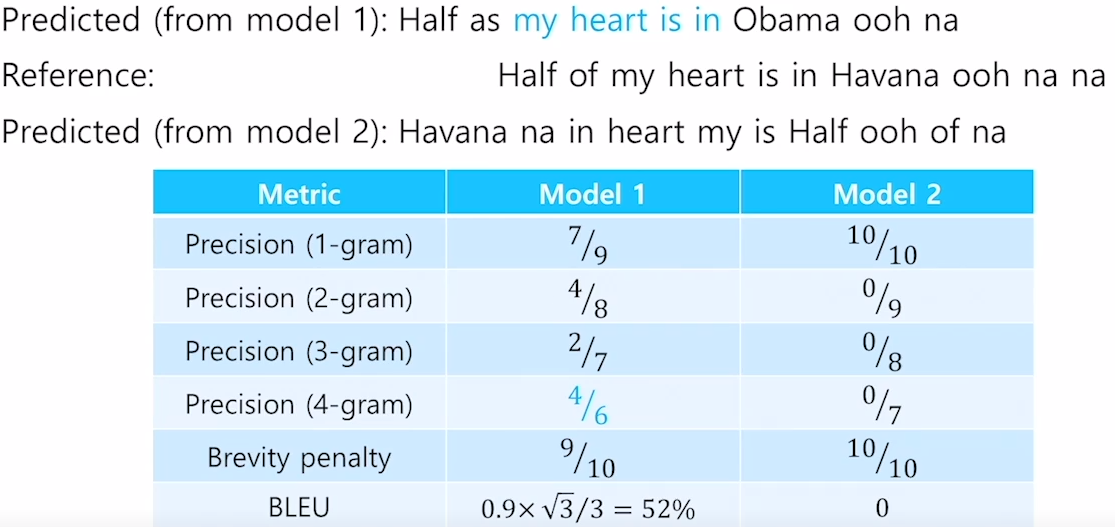
-
Transformer
- Attention is all you need
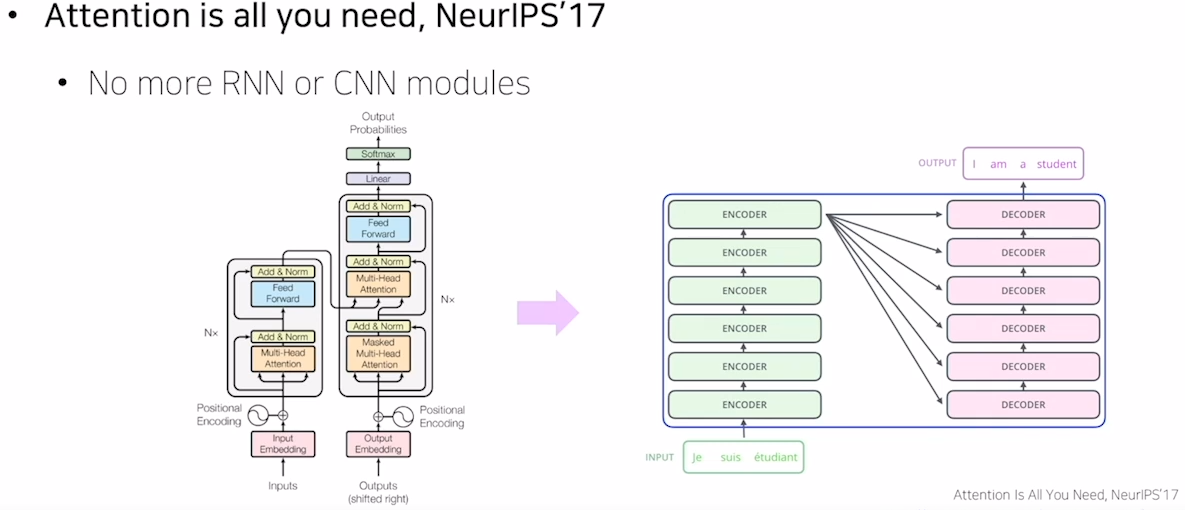
- Long Term Dependency를 해결
- time step을 연속적으로 통과하지 않음
- 연관성을 한번에 계산
- Self-Attention 기법을 사용
- 같은 벡터 내에서 세가지의 역할()이 공유되는 것이 아닌 를 통해 다른 벡터로 선형변환 즉 확장 가능
- 를 통해 벡터를 생성
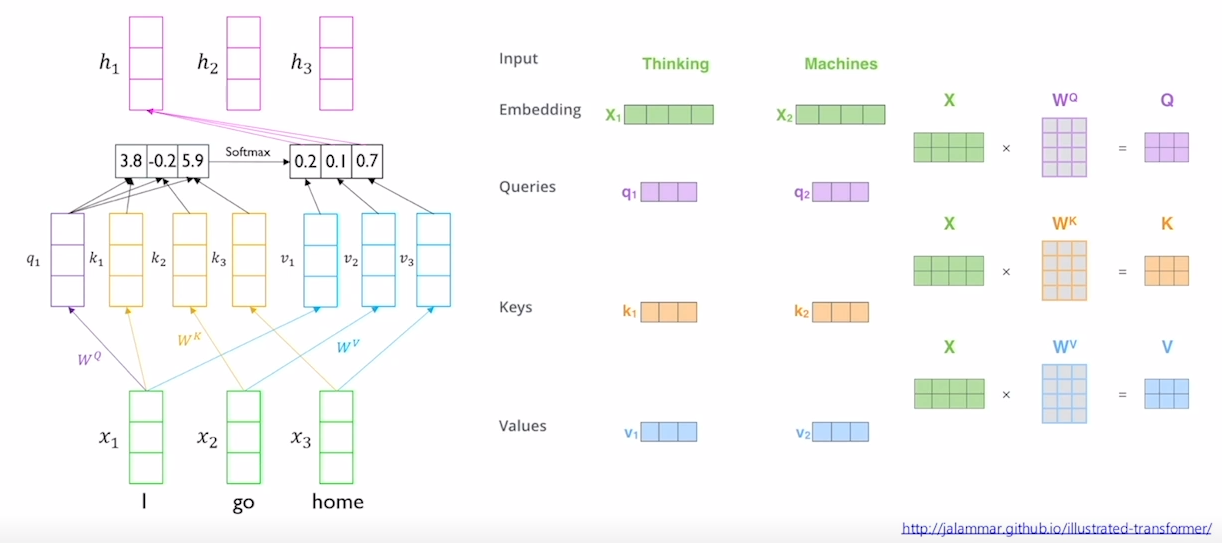
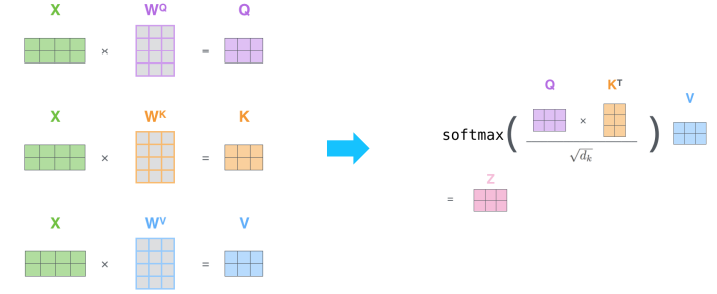
- Scaled Dot-Product Attention
- 가 여러개인 경우 로 변경하여 Row-wise softmax 연산을 사용한다.
- 아래와 같은 연산을 통해 를 구한다.

- : (key)벡터의 dimension에 root를 씌운 값
- 가 커지면 의 variance 또한 커진다
- Some values insside the softmax get large
- The softmax gets very peaked
- Hence, its gradient gets smaller
- So, Scaled by the length of query / key vecotrs
- Attention is all you need
-
Transformer : Multi-Head Attention
- Problem of single attention : Only one way for words to interact with one another
- Solution
- MultiHead() = Concat(headhead)
- where head = Attention()
- is the sequence length
- is the dimension of representation
- is the kernel size of convolutions
- is the size of the neighborhood in restricted self-attention
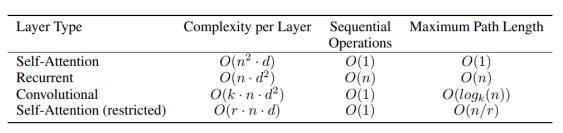
- Self-Attention :
- () :
- : 연산 중 번의 곱셈 및 덧셈
- Recurrent :
- 번의 계산
- Residual Connection
- 기존의 목적함수인 형태로 변환
- 이를 통해 층이 깊어짐에 생겼던 Gradient vanishing을 방지 할 수 있다.
- Layer Norm()
- Positional Encoding
- Use sinusoidal functions of different frequencies
- =
- =
- input data의 차원과 Positional Encoding 차원이 같기에 여러개의 sin,cos 함수를 조합하여 유니크한 위치 벡터를 조합한다.
- sin,cos은 -1~1 사이의 주기함수이기에 여러개의 함수를 조합해야 유니크한 위치 벡터를 만들 수 있다.
- 참고
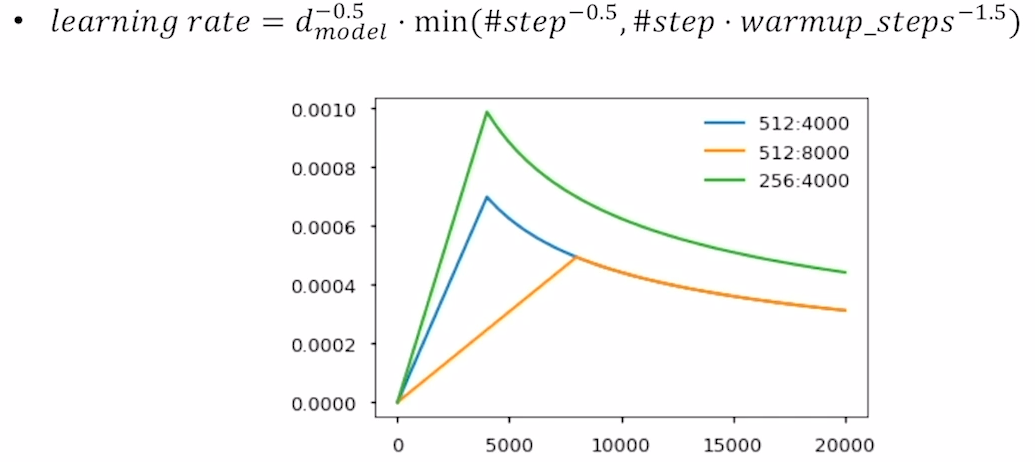
- Warm-up Learning Rate Scheduler
- Masked Self-Attention
- Decoder에 input 데이터는 하삼각행렬을 사용함
- 들어가지 않은 정보의 치팅을 막기 위해
-
9강, 과제 추가하기
출처 : Naver BoostCamp
todo
- Hugging Face(원문)
- Hugging Face(번역)

