정보량부터 VAE까지

City_Duck·2023년 2월 12일

Riffusion

목록 보기

2/6

정보량이란?

정보량의 기원은 어떤 내용을 표현하기 위해 물어야 하는 최소한의 질문 개수에서 출발합니다.

질문개수 = $log_2$ (가능한 결과의 수)로 정의할 수 있으며
해당 내용을 처음 정립한 R.V.L Hartley는 논문에서 정보를 $H$ 로 표현합니다.
즉 $H$ = $nlog$ ( $s$ ) = $log$ ( $s^n$ )
여기서 $n$ 은 받는 정보의 개수, $s$ 는 각 선택에서 가능한 결과의 가지수입니다.

Entropy란?

불확실성(랜덤성)이 적으면 더 적은 정보량을 생성한다.
모든 사건이 같은 확률로 일어나는 것이 가장 불확실하다.
이를 식으로 정립한 것이 바로 Claude Shannon이며, Shannon은 이 불확실성의 측정을 'Entropy'라고 불렀으며 $H$ 라고 표시하였고 단위를 bit라고 하였습니다.
'이산확률분포'일 때 '가능한 결과의 수'는 해당 사건 발생확률의 역수입니다.
위의 계산을 일반화 하면 다음과 같은 식이 도출됩니다.
$\displaystyle\ H = \sum$ (사건 발생확률) $\cdot$ $log_2$ ( $1\over사건 발생확률$ )
$\displaystyle\ = \sum_ip_i \cdot log_2(\frac1{p_i})$
$\displaystyle\ = -\sum_ip_i \cdot log_2(p_i)$
Entropy는 가능한 모든 사건이 같은 확률로 일어날 때 최대값을 얻습니다.

정리하자면, entropy란 최적의 전략하에서 그 사건을 예측하는 데에 필요한 질문 개수를 의미,
다른 표현으로는 최적의 전략 하에서 필요한 질문개수에 대한 기대값

Cross Entropy

Cross Entropy란 어떤 문제에 대해 특정 전략을 사용할 때 예상되는 질문 개수에 대한 기대값

전략은 확률분표로 표현된다.
해당 문제에 대한 최적의 전략을 사용할 때 Cross Entropy의 값이 최소
Cross Entropy의 수식은 다음과 같습니다.
$\displaystyle\ H(p,q) = \sum_ip_i \cdot log_2 \frac1{q_i}$
$\displaystyle\ = H(p,q) = -\sum_ip_i \cdot log_2{q_i}$
$p_i$ 는 특정 확류에 대한 참값 혹은 목표 확률이며, $q_i$ 는 현재 학습한 확률값입니다.
따라서, 어떤 $q_i$ 가 $p_i$ 에 가까워질수록 Cross Entropy 값은 작아지게 됩니다.
이산형이 아닌 연속형의 경우 다음과 같은 수식을 사용합니다.
$- \int p(x) \cdot log q(x)dx$

Cross Entropy와 Cost Function

logistic regresion에서 보던 $-ylog \hat{y} - (1-y)log(1- \hat{y})$ 해당 cost function은 결국 Cross Entropy 수식에 sigma를 풀어쓴 것에 불과했습니다.
Binary의 경우 해당 데이터에 likelihood을 구한 후 log를 붙인 수식은 다음과 같습니다.
$ylog \hat{y} +(1-y)log(1- \hat{y})$ 이 때 해당 수식을 최대화 시키는 즉 likelihood를 최대화 시키는 것은
$-ylog \hat{y} - (1-y)log(1- \hat{y})$ 수식을 최소화 시키는 것과 같습니다.
그렇기에 Cross Entropy는 log loss로 불리기도 합니다.
Cross Entropy를 최소화하는 것은 log likelihood를 최대화하는 것과 같기 때문입니다.
그렇기에 자연스럽게 Cross Entropy는 negative log likelihood로 불리기도 합니다.

KL-divergence

풀네임은 Kullback-Leibler divergence이며 정의는 다음과 같습니다.

두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다.

Cross Entropy로부터 KL-divergence를 수식으로 유도할 수 있습니다.
$\displaystyle\ H(p,q) = -\sum_ip_i \cdot log{q_i}$
$\displaystyle\ =-\sum_ip_i \cdot log{q_i}$ + $\sum_ip_i \cdot log{p_i} - \sum_ip_i \cdot log{p_i}$
$\displaystyle\ = H(p) + \sum_ip_i \cdot log{p_i} - \sum_ip_i \cdot log{q_i}$
$\displaystyle\ = H(p) + \sum_ip_i \cdot log \frac{p_i}{q_i}$
즉 P의 엔트로피에 $\displaystyle\ \sum_ip_i \cdot log \frac{p_i}{q_i}$ 해당 부분이 더해져서 Cross Entropy가 되며, 더해지는 부분이 분포 $p$ 와 $q$ 의 정보량 차이 즉 KL-divergence입니다.
즉, KL-divergence는 $p$ 와 $q$ 의 Cross Entropy에서 $p$ 의 엔트로피를 뺀 값 즉 두 분포의 차이를 나타냅니다.
$KL(p||q) = H(p,q) - H(p)$
그러므로 Cross Entropy를 최소화하는 것은, $H(p)$ 가 고정된 상수값이기에 결과적으로 KL-divergence를 최소화하는 것과 같습니다.

KL-divergence의 특징

$KL(p|q) \geq 0$
$KL(p|q) \neq KL(q|p)$

0 이상이다.

직관적으로는 Cross Entropy에서 entorpy를 뺀 값이기에 0보다 작을 수 없습니다. 즉 lower bound가 entropy입니다.

거리 개념이 아니다.

“KL-divergence는 asymmetric하다” 즉 비대칭적입니다. 이는 수식을 전개함으로써 쉽게 알 수 있습니다.

KL-divergence와 log likelihood

전체를 알 수 없는 분포 $p(x)$ 에서 추출되는 데이터를 모델링하고 싶다고 가정할 때
학습 가능한 파라미터 $\theta$ 의 prarmetric distribution $q(x|\theta)$ 를 이용해 근사시킨다고 가정하겠습니다.
이 $\theta$ 를 결정하는 방법 중 하나는 $p(x)$ 와 $q(x|\theta)$ 사이의 KL-divergence를 최소화시키는 $\theta$ 를 찾는 것입니다.
하지만 $p(x)$ 를 모르기에 $p(x)$ 에서 추출된 몇 개의 샘플 데이터(training set)의 평균을 통해 $p(x)$ 에 대한 기대값을 구합니다.
$\displaystyle\ KL(p||q) \simeq \frac1{N} \sum_{n=1}^N -\ln q(x_n|\theta) + \ln p(x_n)$
$\ln p(x_n)$ 은 $\theta$ 에 대해 독립적이고, $-\ln q(x_n|\theta)$ 는 training set으로 얻은 $q(X|\theta)$ 분포하에서 $\theta$ 에 대한 negative log likelihood입니다.
즉 KL-divergence를 최소화하는 것이 likelihood를 maximize하는 것과 같다는 것을 알 수 있습니다.

KL-divergence와 VAE

$\displaystyle\ D_{KL}(p||q) = \sum_{i=1}^Np(x_i) \cdot (\log p(x_i)-\log q(x_i)$
해당 수식은 원본 데이터 확률 분포와 근사 분포와의 로그 차이 값의 기대값으로 해석할 수 있습니다.
즉 KL-divergence를 통해 잃어버린 정보량, 정보 손실에 대해 알 수 있습니다.
그러므로 KL-Divergence를 잘 활용하면, 신경망의 목적 함수로 사용하여 데이터를 설명하는 모델의 최적 값을 찾을 수 있으며 고차원의 다수 파라미터를 가지는 모델로도 확장할 수 있습니다.

KL-divergence와 Neural Network를 이용하여 매우 복잡한 근사 확률 분포도 학습 시킬 수 있다.

일반적으로 이러한 접근법을 "Variational Autoencoder"라고 합니다.

1차 정리

어떤 내용을 표현하기 위해 물어야 하는 최소한의 질문 개수를 정보량이라고 하며 이를 알기 위해서는 '가능한 결과의 수'를 알 수 있어야합니다.
'가능한 결과의 수'는 해당 사건 발생확률의 역수이며 각 사건의 발생확률과 정보량의 곱의 합을 통해 엔트로피 즉 필요한 질문 개수에 대한 기대값을 얻을 수 있습니다.(= 엔트로피는 정보량의 기대값)
Cross Entropy는 어떠한 문제에 대해 특정 전략을 사용할 때의 엔트로피로 해석할 수 있습니다.
이를 cost function에 적용할 수 있으며 Cross Entropy를 최소화 하는 것은 두 확률 분포간의 차이 즉 KL divergence를 최소화하는 것과 같고 log likelihood를 최대화 하는 것과 같습니다.
이를 Neural Network에 적용하는 접근하는 방법론을 VAE라고 합니다.

Manifold Learning이란?

Manifold란 고차원 데이터가 있을 때 고차원 데이터를 데이터 공간에 뿌리면 sample들을 잘 아우르는 subspace가 있을 것이라는 가정에서 학습을 진행하는 방법

Manifold : 데이터가 있는 공간

Manifold learning은 다음과 같은 용도로 사용됩니다.
1. Data Compression
2. Data Visualization
3. Curse of Dimensionality
4. Discovering most important features

차원의 저주
- 데이터의 차원이 증가할수록 해당 공간의 크기(부피)가 기하급수적으로 증가
- 동일한 개수의 데이터 밀도는 차원이 증가할수록 급속도로 희박해진다.
- 따라서 차원이 증가할수록 데이터 분포 분석 또는 모델 추정에 필요한 샘플 데이터의 개수가 기하급수적으로 증가합니다.

Manifold Hypothesis (assumption)

고차원의 데이터의 밀도는 낮지만, 이들의 집합을 포함하는 저차원의 manifold가 존재한다.
해당 저차원의 manifold를 벗어나는 순간 밀도는 급격히 낮아진다.

즉 고차원의 데이터를 잘 표현하는 manifold를 통해 우리는 샘플 데이터의 특징을 파악할 수 있습니다.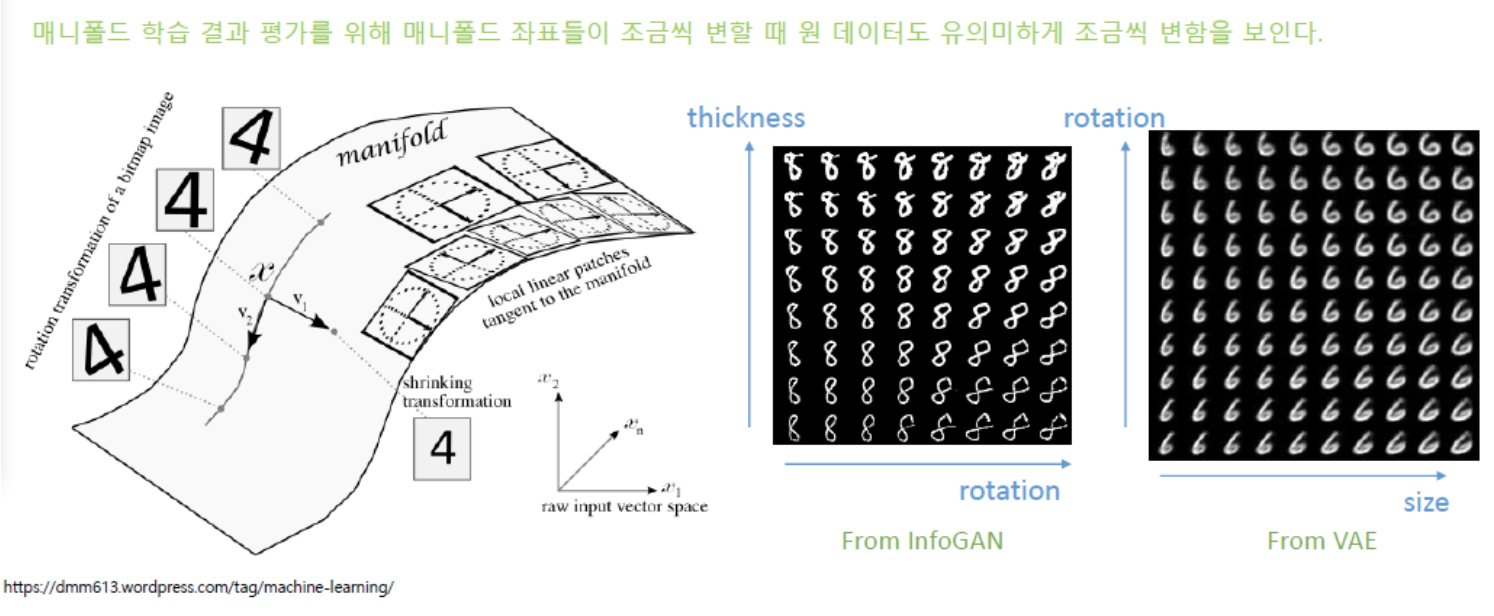 ㄴㅇㄹ
앞서 manifold가 고차원 데이터를 잘 표현한다는 것은 데이터의 중요한 특징을 발견할 수 있다는 것입니다.
그렇기에 고차원 데이터의 manifold 좌표를 조정하면 manifold의 변화에 따라 학습 데이터도 유의미하게 조금씩 변하는 것을 확인할 수 있습니다.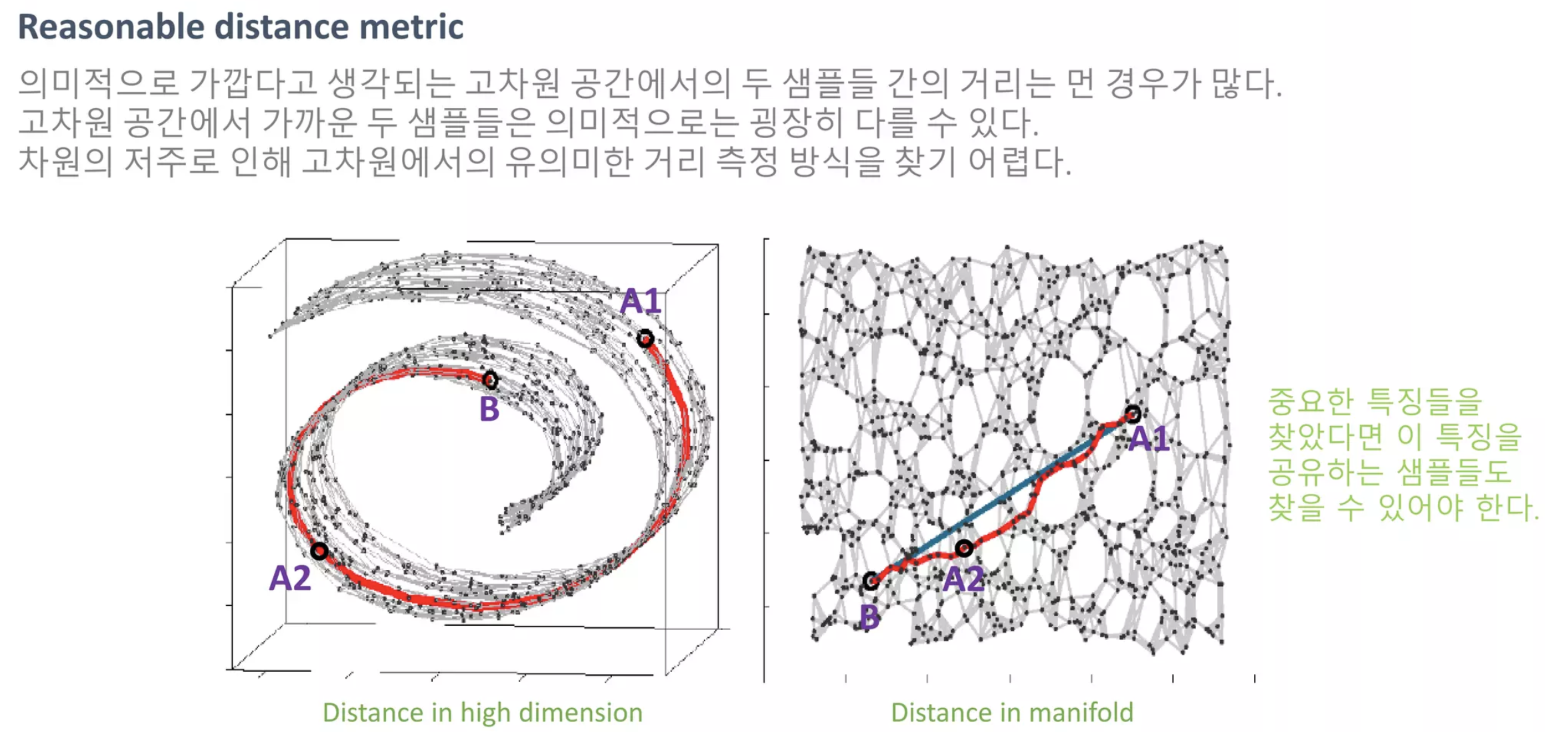 ㅁㄴㅇㄹㅁㄴㅇㄹ
Data(sample)을 잘 아우리는 manifold를 통해 다음과 같은 효과를 얻을 수 있습니다.
1. Feature을 잘 찾았기 때문에 manifold의 좌표를 조금씩 변경하며 데이터를 유의미하게 변화시킬 수 있습니다.
2. 이는 Data의 Dominant한 Feature을 잘 찾았기 때문이며 이는 역으로 manifold를 통해 dominant feature가 유사한 sample을 찾을 수 있다는 점을 시사합니다.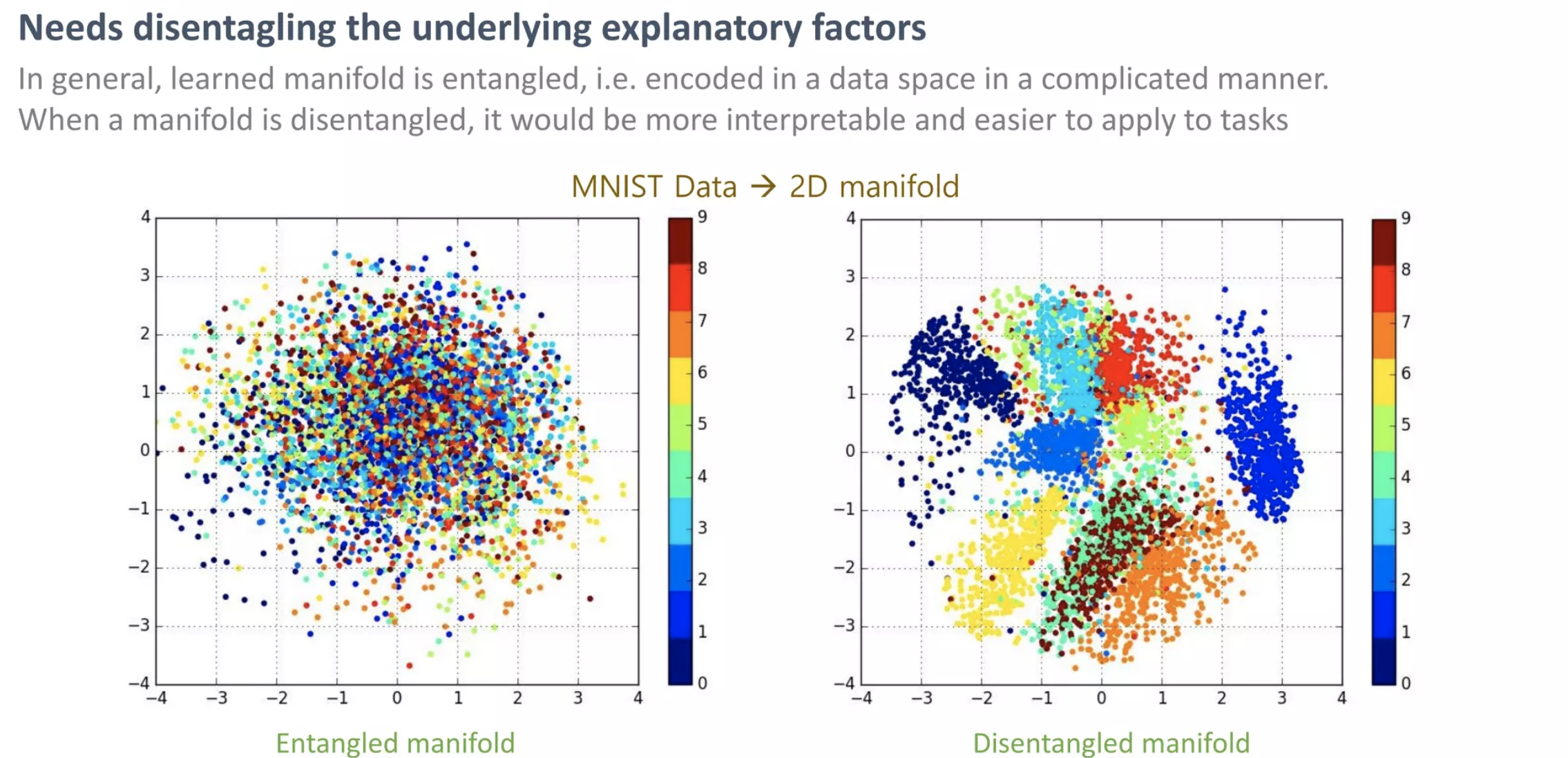 ㅁㄴㅇ
일반적으로 학습된 manifold는 얽혀있으며 이가 풀리면 해석이 쉽고 작업에 쉽게 적용할 수 있습니다.
Dimensionality Reduction는 선형과 비선형으로 구분할 수 있습니다.
1. Linear : PCA, LDA, etc..
2. Non-Linear : AutoEncoder(AE), t-SNE, etc..

AutoEncoder란?

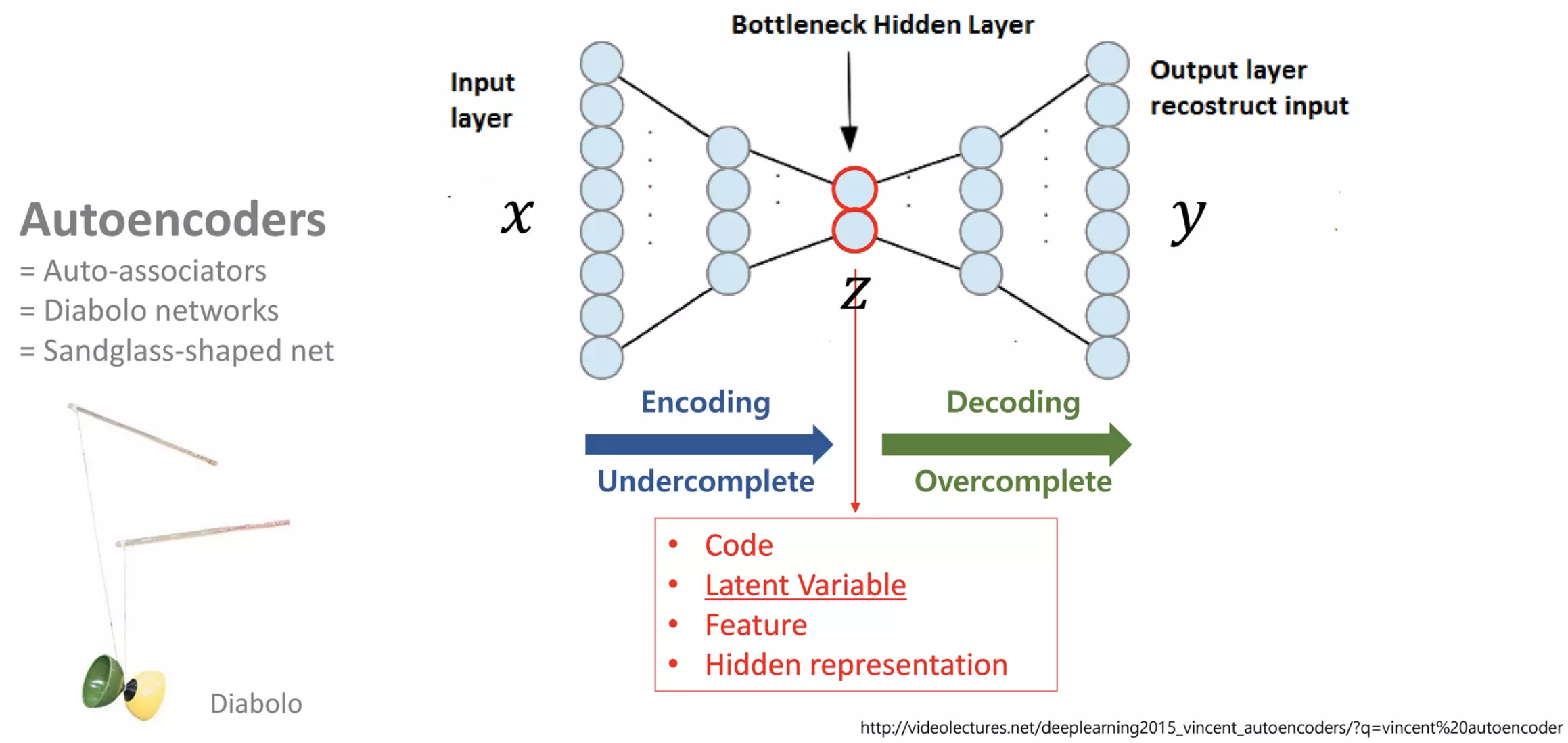
AutoEncoder의 특징으로는 다음과 같습니다.
1. 입력과 출력이 같은 구조
2. Bottlenect Hiddenlayer
3. 비지도학습을 지도학습으로 변경
4. input과 비슷한 output을 만들도록 유도하는 loss
Bottlenect Hiddenlayer는 다음과 같이 표현하기도 합니다.

Latent Variable
Feature
Hidden representation

AutoEncoder의 수식
ㅁㄴㅇㄹ

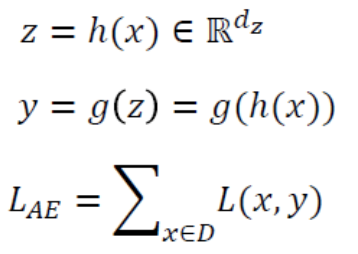
input Data를 Encoder Network에 통과시켜 압축된 z값을 얻습니다.
압축된 z vector로부터 input Data와 같은 크기의 출력 값을 생성합니다.
이 때 Loss값은 입력값 x와 Decoder를 통과한 y값의 차이입니다. (특징 4)

AutoEncoder의 학습 방법

Decoder Network를 통과한 Output layer의 출력 값은 Input값의 크기와 같아야 합니다(같은 이미지를 복원한다고 생각하시면 될 것 같습니다)
이때 학습을 위해서는 출력 값과 입력값이 같아져야 합니다

AutoEncoder의 Encoder

적어도 input data(training set)을 잘 복구한다.
최소한의 성능을 보장한다.

AutoEncoder의 Decoder

최소한 training data를 만들 수 있다.
GAN과 다르게 Loss값으로 인해 성능 보장이 가능하다.

AutoEncoder의 활용 예시

Input data의 feature를 추출할 때 많이 사용한다.
주로 Dimension Reduction에 사용한다.
- network parameter 초기화, pre-training에 많이 사용된다.
- 지금은 Batch-Norm, Xavier Initialization과 같은 기법이 대신한다.

Denoising AutoEncoder

input data에 random noise를 추가합니다.
이 때 random noise란 noise를 추가하더라도 manifold 상에서 같은 위치에 분포되는 정도의 noise 입니다.
즉 manifold상에서는 똑같지만 원본 데이터와는 다른 데이터로 Encoder와 Decoder를 학습하는 네트워크를 Denoising AutoEncoder라고 합니다.
Denoising AE을 통해 이미지를 학습할 경우 학습이 진행될수록 네트워크의 Filter는 low-level에서 high-level feature를 추출할 수 있게 됩니다.
이에 Stacked Denoising 방식을 Denoising AE와 AE에 적용 후 비교할 시 약 25%의 input에 대해 noise를 추가해주는 방식이 Loss값이 가장 낮습니다.

Variational AutoEncoder(VAE)

VAE는 생성모델입니다.

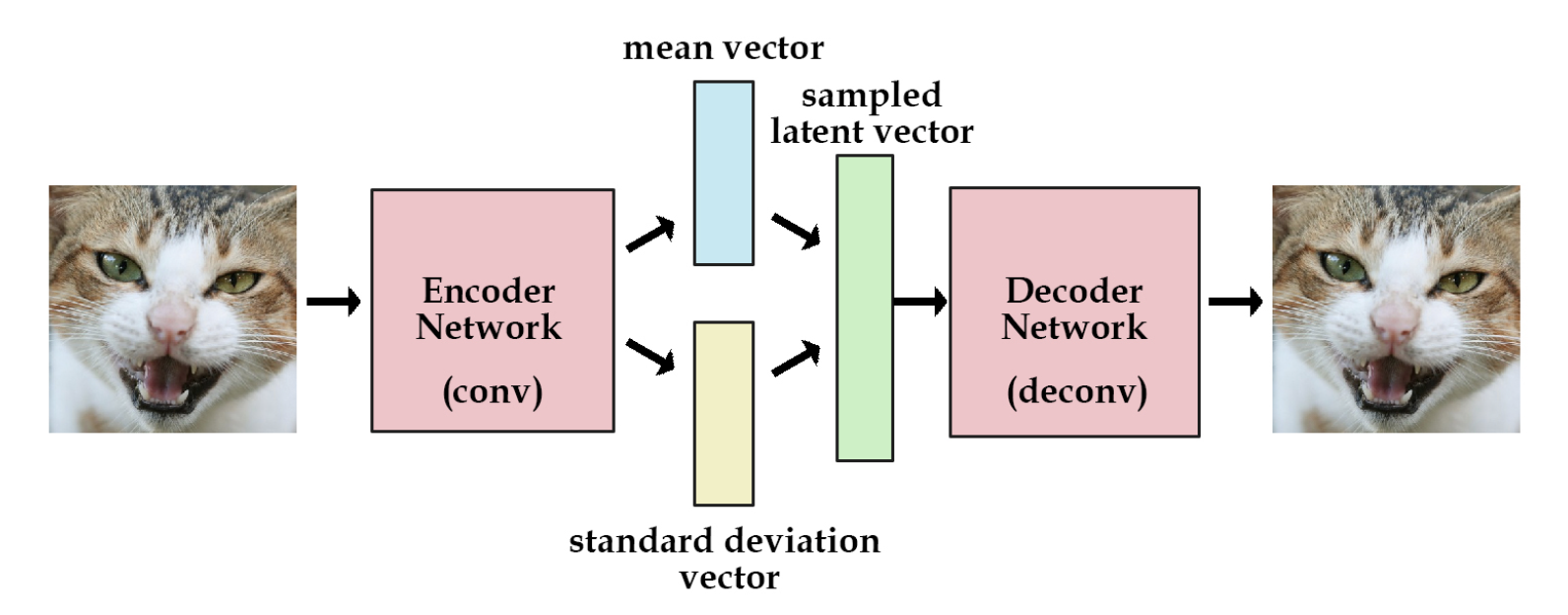
여기에 '생성'은 단순히 Data instance를 생성하는 것이 아닌 Training Data의 분포를 근사하는 특성을 가지고 있습니다.
먼저 VAE와 AE는 전혀 관계가 없습니다.

수학적으로 AE와 VAE는 전혀 관계가 없습니다.

AutoEncoder의 목적은 Manifold Learning
VAE의 목적은 Generative Model이며 Decoder을 학습시키기 위해 Encoder를 붙였을 때 공교롭게도 구조가 AE와 같습니다.
결론적으로 두 모델은 단지 이름과 모양만 비슷합니다.

VAE의 학습 목적은 Training DB에 있는 데이터 x가 나올 확률을 구하는 것 입니다.
이를 해당 모델의 출력값을 MLE 값을 통해 구할 것입니다.
또한 VAE의 Generator는 Latent Variable z로부터 샘플을 생성합니다.
이에 z vector를 controller처럼 이미지를 조정하는 컨트롤러로 사용합니다.

Prior Distribution

기존 Training DB에 있던 샘플과 유사한 샘플을 생성하기 위해서 prior값을 사용합니다.
prior값이 normal distribution와 같은 간단한 분포를 띈다고 가정하고 sampling을 진행해도 sampling 된 값은 manifold를 대표하는 값을 가질 수 있습니다.
이는 학습을 수행하는 네트워크가 Deep Neural Network이기 때문에 가능합니다.
하지만 해당 분포에서 바로 MLE를 수행할 수는 없습니다.
생성기(Generator)에 대한 확률 모델을 가우시안으로 할 경우, MSE관점에서 더 가까운 것이 더 p(x)에 기여하는 바가 크게 됩니다. MSE가 더 작은 이미지가 의미적으로는 더 가까운 경우가 아닌 이미지들이 많기 때문에 현실적으로 올바른 확률 값을 구하기는 어렵습니다.
이를 해결하기 위해 Variational Inference 방법을 사용합니다.

Variational Inference

이제는 prior에서 sampling 하는 것이 아닌 이상적인 sampling함수를 통해 samplilng을 수행합니다.
이의 목표는 네트워크의 출력 값이 x와 가까워지는 것입니다.
이를 위해 다음의 3-step을 밟습니다
Step 1. 의미론적으로 가까운 sample들을 생성시키는 z 정의
Step 2. z를 생성할 수 있는 이상적인 sampling 함수 정의
Step 3. x를 given으로 주어 학습을 수행
p(z|x)가 아닌 이상적인 sampling함수인 qΦ(z|x)를 추정하고 이상적인 sampling함수가 정의되었다면 z vector로부터 Input x와 유사한 데이터를 생성할 수 있게 됩니다.

Variational Inference

True posterior: 우리가 추정하고자 하는 확률분포
Approximation class: 우리가 다루기 쉬운 확률 분포(e.g Gaussian, Bernulli)
- Gaussian일 경우 확률분포를 결정짓는 파라미터 μ와 𝜎를 추정
- Φ를 잘 바꿔가며 True posterior를 추정(Approximation)
- 학습이 잘 될 경우, True posterior를 잘 approximation 하는 함수를 가지고 z생성
- 생성된 z를 통해 sample을 생성
term 정리
- true posterior: p(z|x) - how likely the latent variable is given the input
- prior: p(z) - how the latent variables are distributed without any conditioning
- approximation function(sampling function): q(z|x)

ELBO

p(x)의 최대값을 구하기 위해 log값을 씌워 전개를 합니다.

해당 두 수식의 전개를 통해 다음의 최종 수식을 얻을 수 있습니다.

결론적으로 다음과 같은 수식을 최적화하는 문제로 정의할 수 있습니다.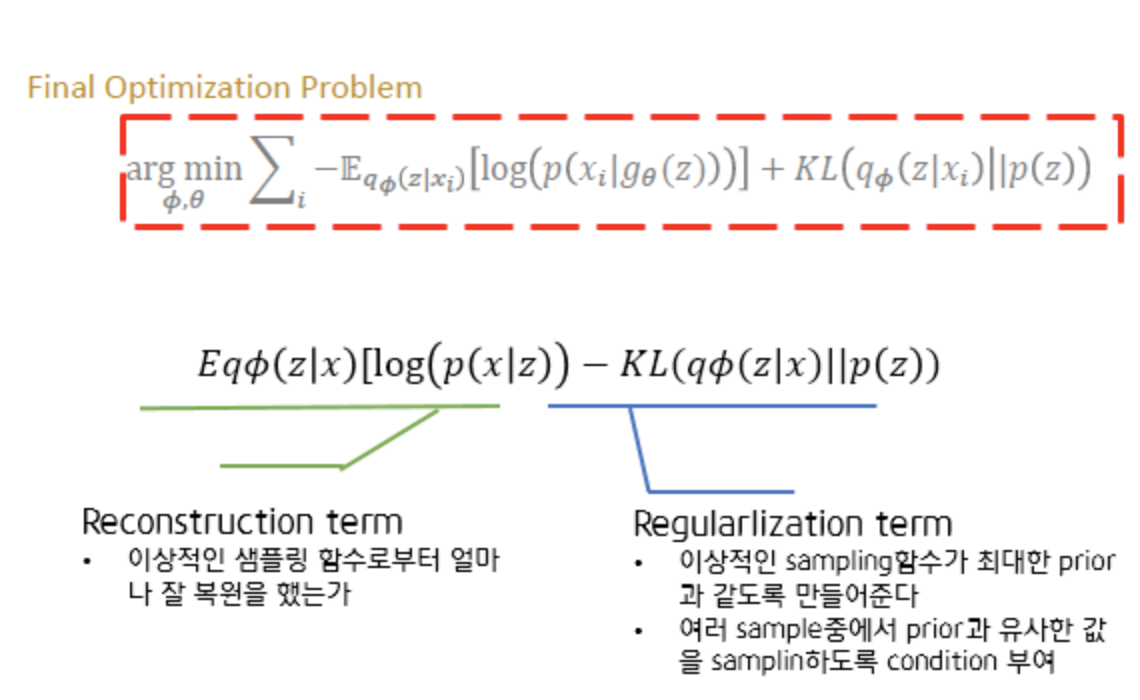

즉 Generator를 학습기 위해 prior 값만으로는 부족하기에 이상적인 sampling 함수 qΦ(z|x)를 도입합니다.
x를 evidence로 주고, x에 대해서 Generator가 잘 학습할 수 있도록 만들어주는 z를 sampling 하기 위해서 qΦ(z|x)를 도입한 것입니다. 그리고 sampling 한 값이 input값과 같아줬으면 하기 때문에(Reconstruction Term), 𝜃를 최적화시키는 MLE문제로 풀 수 있습니다.

정리하자면 학습 과정으로는 ELBO term을 Φ에 대해 maximize 하면 이상적인 sampling함수를 찾는 것이며 ELBO term을 𝜃에 대해 maximize 하면 MLE 관점에서 Network의 파라미터를 찾는 것입니다.

이때 Training DB에 있는 Input Data와 비슷하게 복원되어야 한다는 조건(condition)은 'reconstruction term'에 녹아있고, reconstruction이 잘 된 이상적인 sampling함수의 z값이 prior(p(z))와 같았면 좋겠다는 조건(condition)을 'regularization term'에 녹여주면 되는 것입니다.

AutoEncoder와 Variational AutoEncoder

그렇다면 AutoEncoder로 학습한 것과 Variational AutoEncoder로 학습했을 때 가장 큰 차이는 무엇일까요?

결론부터 말씀드리면 AutoEncoder는 'prior에 대한 조건(Condition)'이 없기 때문에 의미있는 z vector의 space가 계속해서 바뀌게 됩니다. 즉 새로운 이미지를 생성할 때 z 값이 계속해서 바뀌게 됩니다.

반면 Variational AutoEncoder의 경우 prior에 대한 Condition을 부여했기 때문에 z vector가 prior과 같은 분포를 따릅니다. e.g prior가 Normal distribution이라면 z vector도 같은 분포를 갖는다.
따라서 prior에서 sampling을 하면 됩니다.

발췌 : 초보를 위한 정보이론 안내서
발췌 : KL Divergence 설명
발췌 : AutoEncoder의 모든 것
통계학에서의 Parameter