오늘은 BOJ 1520 내리막길 문제를 다시 풀어보았다. 약 1-2주? 전에 풀었던 문제인데, 몇일동안 우연히 BFS 문제를 여러개 풀어보면서 자연스레 DFS가 가물가물 해진다고 느꼈다. DFS 문제를 풀어봐야겠다고 생각했고, BFS 로 풀었던 문제를 다시 복습할 겸 DFS 를 적용해서 풀어보았다!
BOJ 1520 내리막길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
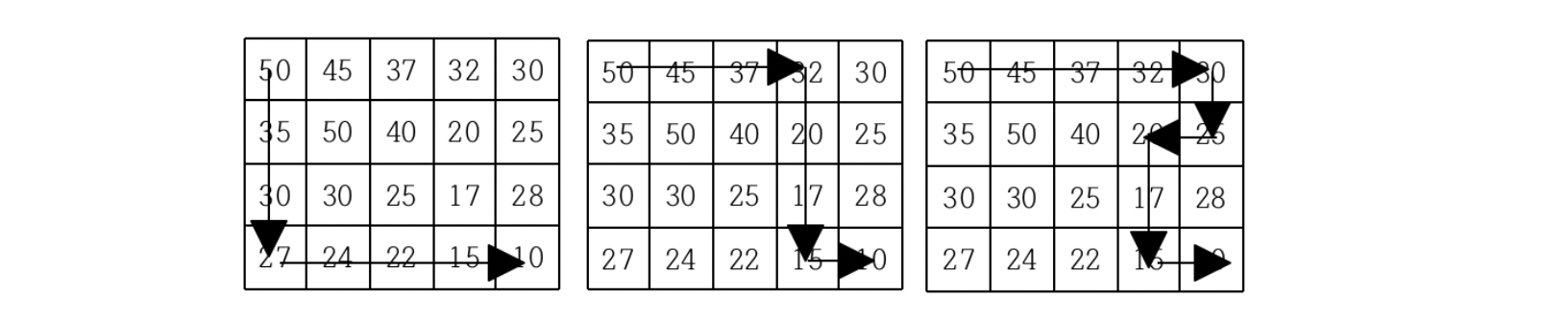
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
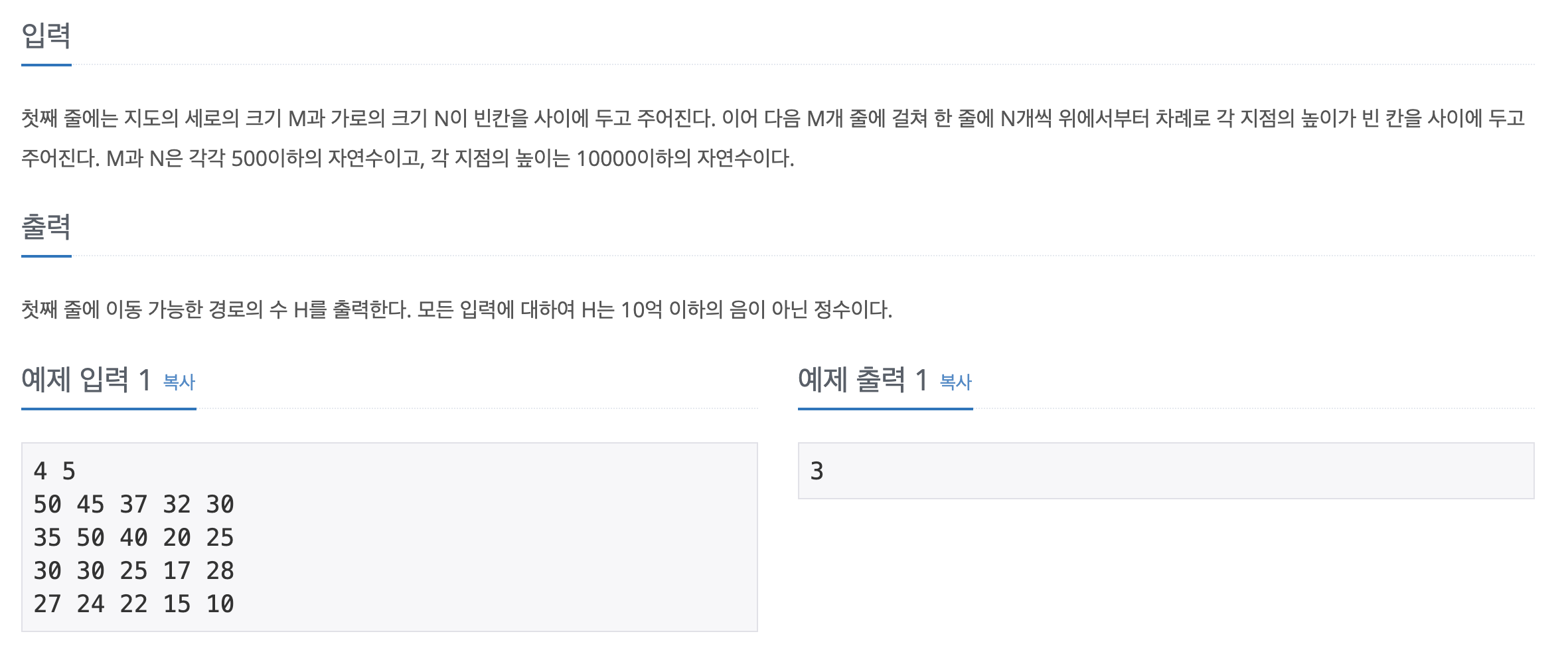
입출력
나의 풀이
시간 초과 발생
이것이 과연 나의 풀이가 맞는가,, ㅜㅡㅜ 속상하지만,, 잊지 않기 위해서 적어본다!
DFS 이기 때문에 stack을 사용해서 풀기를 시도하였다! 출발점 [0,0] 에서 시작해 상하좌우 좌표 중 현재 칸 보다 낮은 칸이 존재하면 해당 칸의 좌표를 stack 에 넣어주고, 넣어주면서 해당칸의 dp 값을 1씩 증가시켜 주었다!
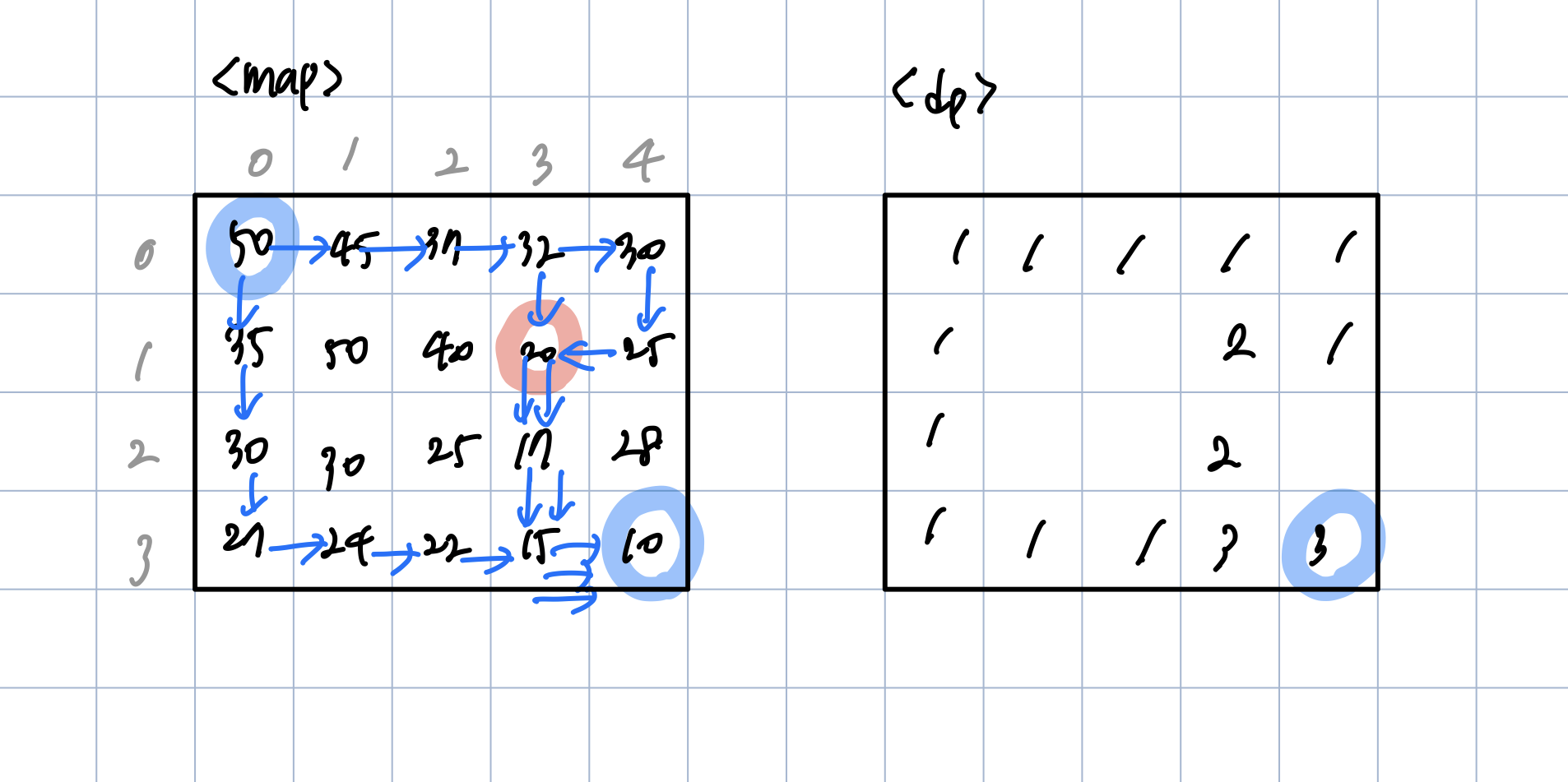
하지만 이와 같은 방법으로 진행한다면 왼쪽 그림의 [1,3] 은 2번 방문하게 되고 [1,3] -> [2,3] -> [3,3] 의 흐름 역시 중복해서 일어난다. 즉
< map > 그림에 표시된 모든 파란 화살표 대로 방문이 이루어 지게 되어 시간 초과가 발생하게 된다.
즉 방문 가능한 모든 지점은 단 한번씩만 방문이 되도록 해야 하는 것이었다.
하지만 stack을 그대로 사용하려니 방법이 떠오르지 않았고,, 아무래도 재귀함수를 사용해야 할 것 같아 친구의 포스팅의 도움을 받아 다시 작성하였다!
재귀 함수 사용
여기선 dp배열에 담기는 값의 의미가 조금 달라진다. 위의 방법에선 dp[i][j] 에 담기는 값이 [i, j] 까지 올 수 있는 경로의 수를 의미했다면, 여기서 dp[i][j] 란 [i, j]에서 [M-1, N-1]까지 갈 수 있는 경로의 수를 의미한다.
즉, 최종적으로 정답은 dp[0][0] 에 담긴 값이 되는 것이다.
시작 전에, dp배열의 모든 값은 -1로 초기화된다. [i, j] 보다 낮은 칸 [nr, nc]를 찾으면 dp[i][j] 에 dp[nr, nc] 값을 더해주게 되는데 이 과정에서 재귀함수 호출이 일어난다. 즉 재귀함수의 반환값 자체가 dp 배열 [i, j]에 담긴 값인것이다.
그림으로 좀 더 자세하게 표현하면,
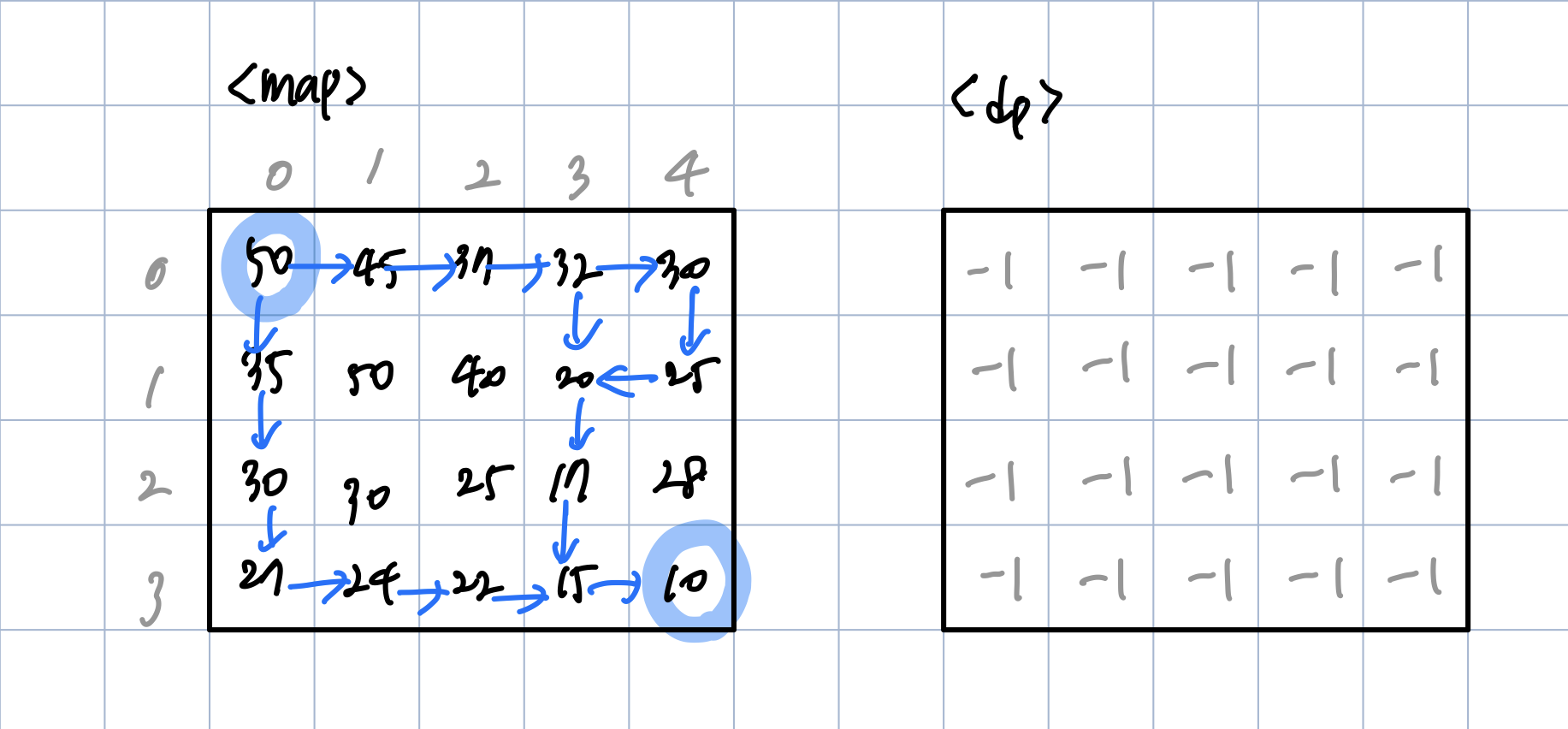
이와 같은 상태에서 [0,0]부터 탐색이 시작되고,
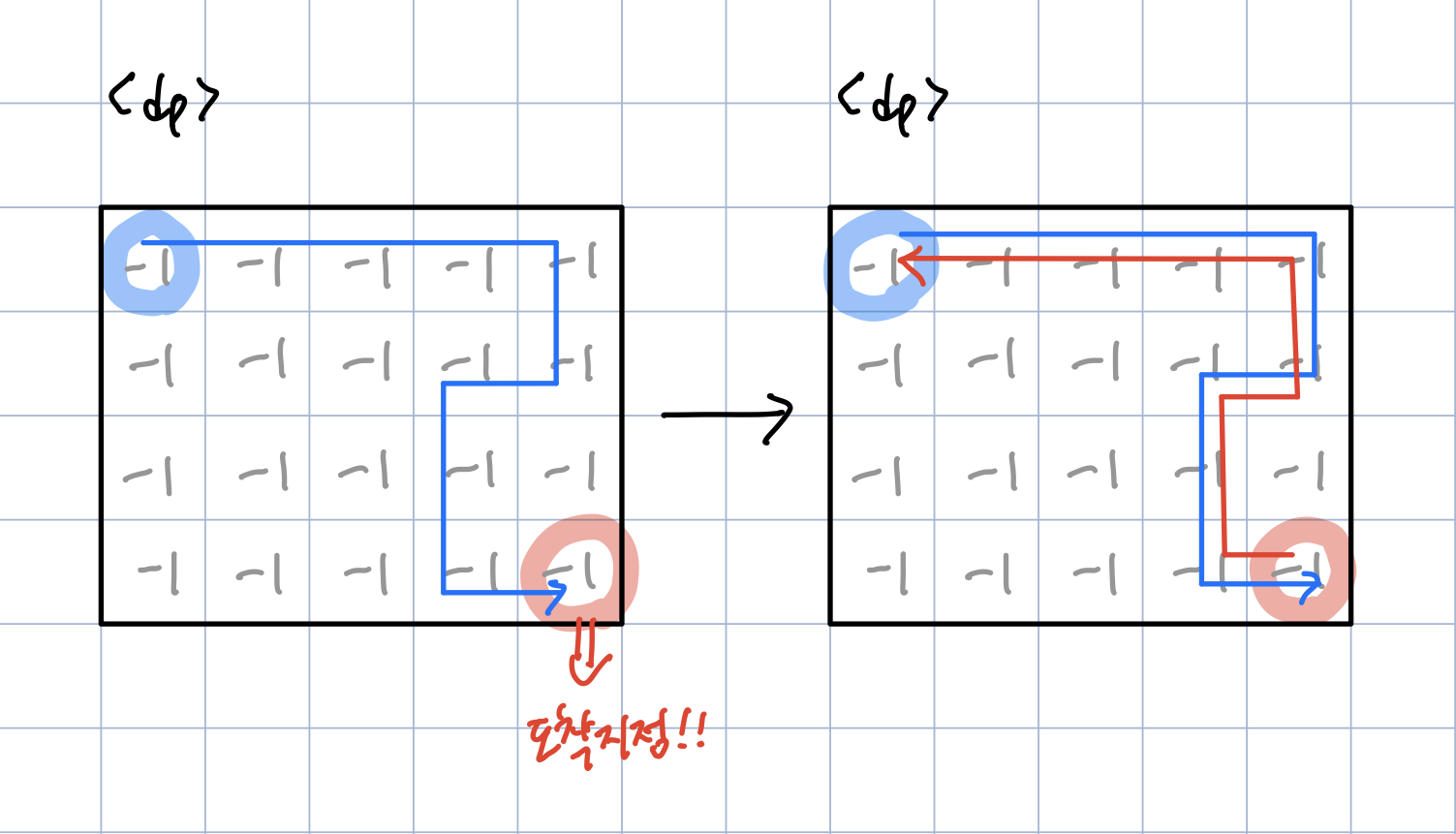
[0,0] 에서 반복적으로 재귀함수가 호출되다가 도착지점을 만나면 dp[M-1][N-1] = 1을 return 하고 왔던 길을 되돌아가면서 dp 값을 더해주는 것이다!

이 때, [0,3] 지점에서 [0,4] 로 가는 경우와 [1,3]으로 가는 경우가 존재하기 때문에 만약 [0,4] 로 먼저 재귀함수가 진행되면 [1,3]을 방문한 이후 dp[1][3] 에는 1이 저장되고 [0,3]->[1,3]으로 재귀가 다시 진행될 수 있다.
이러한 경우를 방지하기 위해 재귀함수 호출 전 만약 해당 칸의 dp 값이 -1이 아니라면, 즉 이미 한번 방문 했다면 바로 해당 칸의 dp 값을 return 하는 코드를 추가해야 한다.
이와 같은 방식으로 진행하면 가능한 경로상에 있는 모든 노드들이 한번씩만 방문되어 시간초과를 피해갈 수 있다..!
코드
#include <iostream>
#include <vector>
// BOJ 1520 내리막길, DFS + DP 로 풀기
using namespace std;
vector<vector<int>> map;
vector<vector<int>> dp;
int dy[4] = {-1, 0, 1,0};
int dx[4] = {0, 1, 0, -1};
int DFS(int row, int col, int M, int N){
// 도착지점
if (row == M-1 && col == N-1) return 1;
// 한번 방문되어 dp 값이 저장되엉 있는 경우라면 다시 방문하지 말고 해당 dp 값 가져와서 더라기
if (dp[row][col] != -1) return dp[row][col];
// 경로수를 더하기 위해 해당 값을 -1 -> 0으로
dp[row][col] = 0;
for (int i = 0; i < 4; ++i) {
int nr = row + dy[i];
int nx = col + dx[i];
// 지도 범위 내 현재 위치보다 낮은 곳으로 재귀 진행
if (nr>=0 && nr<M && nx>=0 && nx<N && map[nr][nx] < map[row][col]) {
dp[row][col] += DFS(nr, nx, M, N);
}
}
return dp[row][col];
}
int main() {
int M, N;
cin>>M>>N;
dp.assign(M, vector<int>(N, -1));
map.assign(M, vector<int>(N, 0));
for (int i = 0; i < M; ++i) {
for (int j=0; j<N; j++){
cin>>map[i][j];
}
}
// 0,0 에서 M-1, N-1까지 갈 수 있는 경로수 = DFS(0,0, M, N)
int answer = DFS(0,0, M, N);
cout<<answer;
return 0;
}어렵다,, ㅜㅜㅜ dfs, 재귀 더 연습한다!!
