[알고리즘 풀이 분석] BOJ 9084 동전

오늘 풀어본 두번째 문제는 BOJ 9084 동전 이다.
오늘부터는 DP 문제를 풀어볼 생각으로 선택한 문제인데, 음,, DP,, 심각하다 ㅋ 나의 DP 능력은 뭔가 접근 법은 알고 있는데,,, 경험이 부족해서 점화식 세우는게 오래 걸리거나 안되는 것 같다. 는 나의 생각이다 암튼,, 우울하다 ㅜ

BOJ 9084 동전

우리나라 화폐단위, 특히 동전에는 1원, 5원, 10원, 50원, 100원, 500원이 있다. 이 동전들로는 정수의 금액을 만들 수 있으며 그 방법도 여러 가지가 있을 수 있다. 예를 들어, 30원을 만들기 위해서는 1원짜리 30개 또는 10원짜리 2개와 5원짜리 2개 등의 방법이 가능하다.

동전의 종류가 주어질 때에 주어진 금액을 만드는 모든 방법을 세는 프로그램을 작성하시오.

입출력

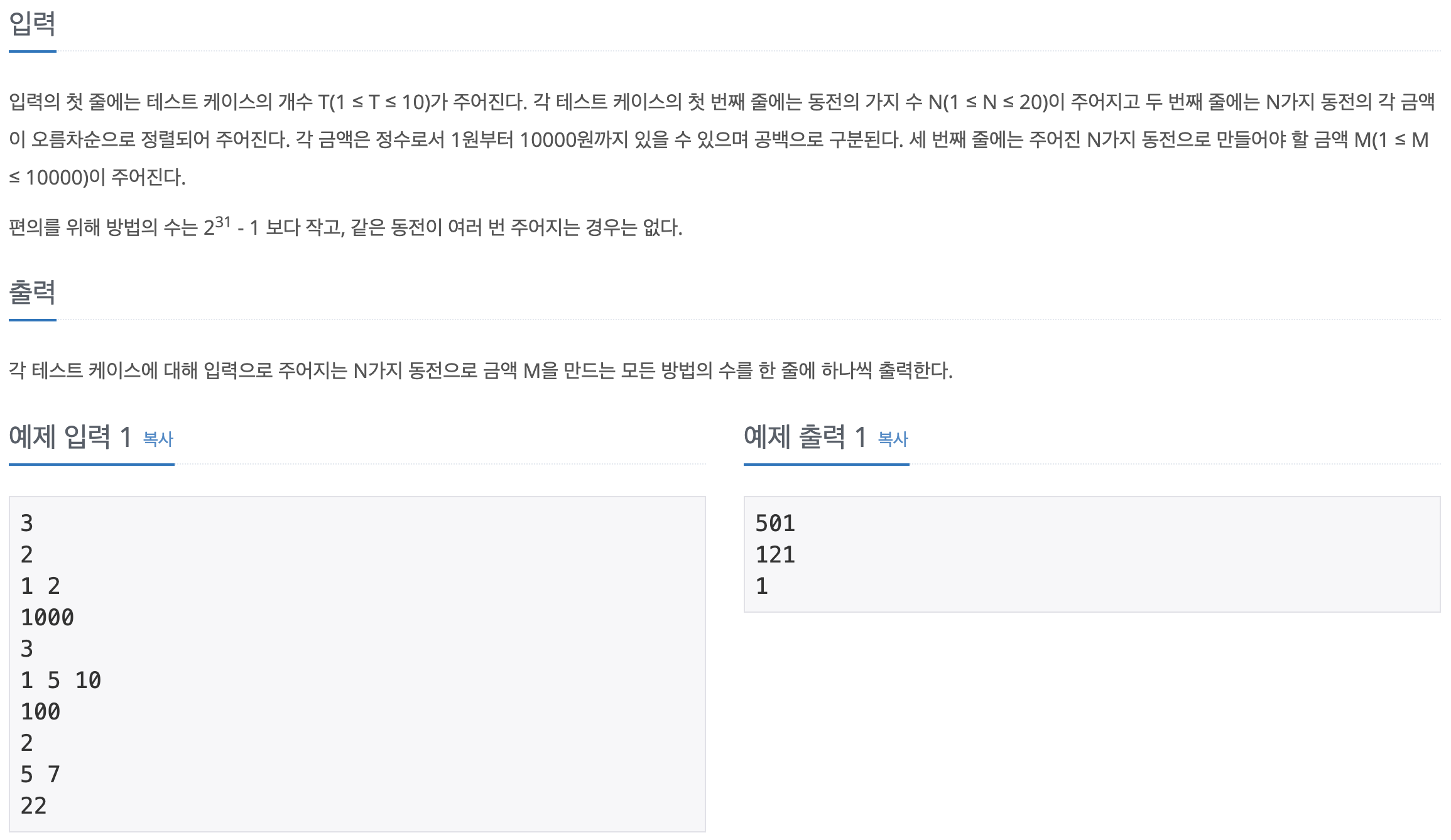
나의 풀이

는 나의 풀이가 아니다 ㅋ,, 100% 내 힘으로 푼 것이 아니기 때문 ^_ㅜ,,,,

입력되는 동전들을 사용해서 주어진 금액을 만들 수 있는 경우의 수를 출력하는 아주 전형적인 DP 문제이다.

문제를 읽고 바로 점화식이 필요할 것이라 생각은 했지만 일관성을 발견하기 어려웠다,, 주어진 3가지 케이스 안에서도 발견하지 못했고 결국 다른 분들의 풀이를 찾아 공부해서 풀었다.

내가 도움을 받은 포스팅에서는 '가장 마지막에 x원을 더하는 경우' 의 개념을 사용하였다.
입출력으로 주어진 3번째 케이스, 2가지 동전 [5,7]로 22원을 만드는 경우를 생각해보자.

최소 금액인 5원부터 시작하면,

가장 마지막에 5원을 더해 5원을 만드려면? -> 0원 + 5원
0원을 만드는 경우는? 모든 동전을 사용하지 않는 경우 1개 뿐이다. dp[5] = 1 (dp[0])

가장 마지막에 5원을 더해 6원을 만드려면? -> 1원 + 5원
그런데 1원을 만들 수 있는 경우가 있는가? 불가능하다. dp[6] = 0

가장 마지막에 5원을 더해 10원을 만드려면? -> 5원 + 5원
5원을 더하기 전 5원을 만드는 경우는? 위에서 이미 구한 값을 사용하면 된다. dp[10] = dp[5] // 1

그럼 이번엔 7원짜리 동전을 사용해보자.

가장 마지막에 7원을 더해 7원을 만드려면? -> 0원 + 7원
5원을 사용했을 때와 동일하게 dp[7] = 1 (dp[0])

가장 마지막에 7원을 더해 14원을 만드려면? -> 7원 + 7원
7원을 만드는 경우는 1가지 이므로 dp[14] = dp[7] // 1

그럼 12원을 만드는 경우는 어떠할까?

가장 마지막에 5원을 더해 12원을 만드려면? -> 7원 + 5원 dp[12] = dp[7]
가장 마지막에 7원을 더해 12원을 만드려면? -> 5원 + 7원 dp[12] = dp[5]

음,, 그럼 12를 만드는 경우는 마지막에 5를 더하는 경우와 7을 더하는 경우가 있으니까 dp[5] + dp[7] = 2 인가??

댓츠노노,,,,
5+7, 7+5 는 동일한 경우이다!!!!!!

나는 이 부분을 해결하는 것에서 고민을 좀 할 수 밖에 없었다.
아니,, 다들 이렇게 풀었는데 통과를 했다고?? 이건 중복인데?? 왜지????

이 부분을 수정하기 전 나의 풀이는 완성하려는 금액에 초점을 맞추고 있었다.
반복문의 큰 기준이 금액 M원이고, M원을 완성하기 위해 마지막에 5원을 더하는 경우와 7원을 더하는 경우를 순서대로 탐색하여 dp 배열에 더해주다보니 이러한 중복된 경우를 잡을 수 없었다!

순서를 주어진 동전들에 맞춰보자.
동전은 5 -> 7 순서로 dp 배열 값을 더해간다고 생각하고 현재 dp 배열의 모든 값은 0이다. 시작 전 0원을 만드는 경우, 즉 어떠한 동전도 선택하지 않는 경우를 dp[0]=1로 채워준다.

5를 마지막에 더해서 5, 10 을 완성하고 12를 보자.
5를 마지막에 더해서 12를 완성하려면 7이 필요하다. 그런데 현재 7을 완성할 수 있는 경우는 몇가지인가?
없다! 우리는 현재 동전 5를 처음으로 가지고 돈을 완성해가는 중이고 7은 5를 마지막에 더해 완성할 수 없으므로 dp[7]의 값은 현재 0이다.
때문에 dp[12] += dp[7] -> 0 이 채워진다.

이후 동전 7로 탐색할 때는 어떠한가?
7을 마지막에 더해 12를 완성하는 경우는 5를 완성하는 경우와 동일하고 dp[5] 는 동전 5로 돈을 완성할 때 1의 값으로 채워져 있는 상태이다. 즉 여기서 dp[12] += dp[5] -> 1로 경우의 수가 올바르게 도출된다!

설명이 좀 길었지만, 동전을 기준으로 하여 중복되는 경우가 없도록 하면 점화식은 dp[n] += dp[n-coin] 임을 알 수 있다. n-coin 이 0보다 작으면 프로그램이 에러가 나게 되므로 n의 값은 가장 작은 coin 값부터 시작하도록 해주면 if 문 처리 없이 코드가 완성되게 된다!

코드

#include <iostream>
#include <vector>

// BOJ 9084 동전, DP, 골드 5,,, 찾아보고 통과함 ㅜㅡㅜ
using namespace std;

int getWayToMake(int M, vector<int> coins){
    vector<int> dp(M+1, 0);
    dp[0] = 1;  // 어떠한 동전도 사용하지 않는 경우 

    for (int i = 0; i < coins.size(); ++i) {
        int coin = coins[i];  
        
        // coin(작은 동전부터)을 마지막에 더해서 j원을 완성하는 경우 탐색 
        for (int j = coin; j <= M ; ++j) {
            dp[j] +=  dp[j-coin];  // j-coin 원을 완성했던 경우에 마지막에 coin을 더하는 경우와 동일 
        }
    }

    return dp[M];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int T, N, M;
    cin>>T;
    vector<int> answers;

    for (int i = 0; i < T; ++i) {
        cin>>N;

        vector<int> coins(N, 0);
        for (int j = 0; j < N; ++j) {
            cin>>coins[j];
        }

        cin>>M;
        int ans = getWayToMake(M, coins);
        answers.push_back(ans);
    }


    for (int i = 0; i < T; ++i) {
        cout<<answers[i]<<'\n';
    }
    return 0;
}

ㅜㅡㅜ DP 부순다 이번주!!!!!!!🔥🔥🔥

백준 9084 동전 (C++)