오늘 두번째로 풀어본 문제는 BOJ 15988 1,2,3 더하기 3 이다!
고럭키씨가 푸셨길래 나도 마침 DP를 풀고 싶어서 따라 풀었다 ㅎㅎ
BOJ 15988 1,2,3 더하기 3
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
입출력
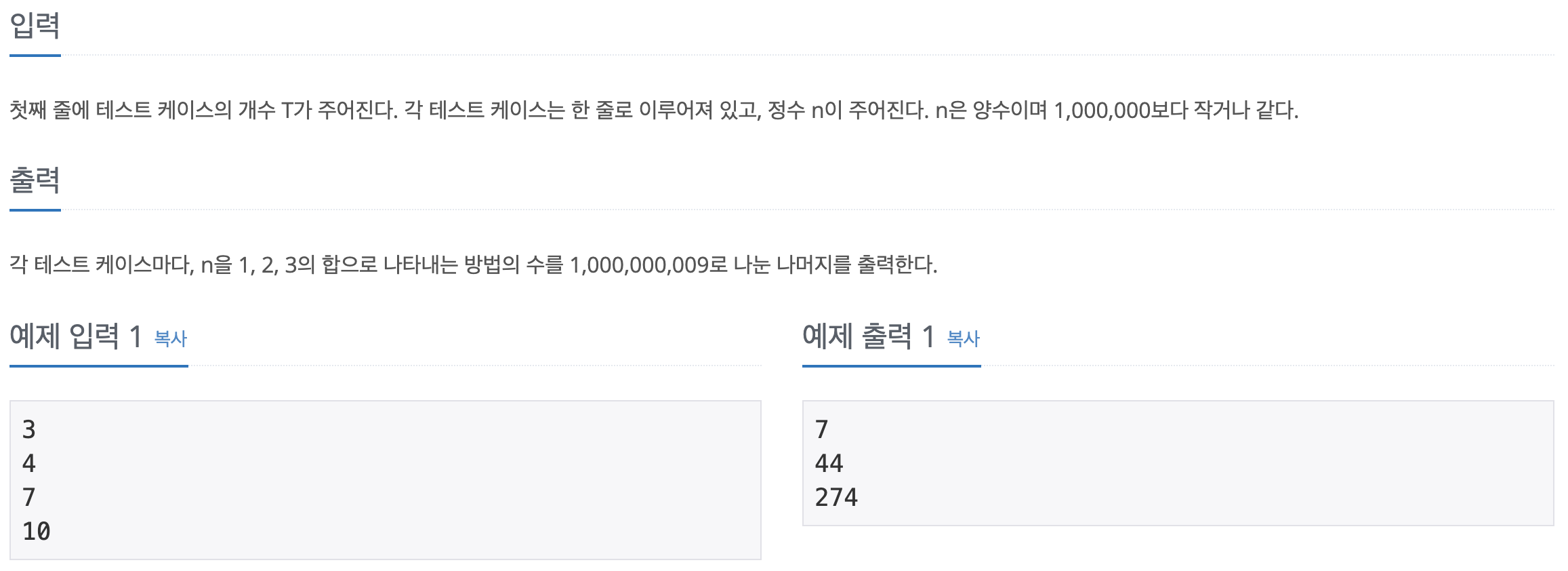
나의 풀이
간단한 DP 문제이다!
1,2,3으로만 주어진 숫자를 완성하는 방법의 수를 찾는 문제이고 예시로 주어진 4를 만드는 경우를 보면 1+3 과 3+1이 각각 경우의 수로 count 되는 것으로 보아 숫자가 사용된 순서에 따라 다른 경우로 체크 되는 것을 알 수 있다!
1 만들기
- 1을 사용해서 1을 만드는 경우의 수 : 0+1 (0 만드는 경우의 수와 동일)
- 2, 3을 사용할 수 없음
➡️ dp[1] = 1
2 만들기
- 1을 사용해서 2를 만드는 경우의 수 : 1+1 (1 만드는 경우의 수와 동일)
- 2를 사용해서 2 만드는 경우의 수 : 0+2 (0만드는 경우의 수와 동일)
- 3을 사용할 수 없음
➡️ dp[2] = dp[1] + dp[0] = 2
3 만들기
- 1을 사용해서 3를 만드는 경우의 수 : 2+1 (2 만드는 경우의 수와 동일)
- 2를 사용해서 3를 만드는 경우의 수 : 1+2 (1 만드는 경우의 수와 동일)
- 3을 사용해서 3를 만드는 경우의 수 : 0+3 (0 만드는 경우의 수와 동일)
➡️ dp[3] = dp[2] + dp[1] + dp[0] = 4
모든 경우의 수가 중복되지 않으므로 점화식은 dp[i] = dp[i-1] + dp[i-2] + dp[i-3] 로 결정된다!
이 때, 주의할 점은 출력시 " n을 1, 2, 3의 합으로 나타내는 방법의 수를 1,000,000,009로 나눈 나머지를 출력한다. " 이다.
dp 배열의 자료형은 int 로 한다면 int 의 최댓값은 2,147,483,647 이기 때문에 점화식 dp[i] = dp[i-1] + dp[i-2] + dp[i-3] 과정에서 int 자료형 overflow 가 발생할 수도 있다.
또, dp[i-1], dp[i-2], dp[i-3] 을 모두 1,000,000,009 로 나눈 나머지 값을 각각 더해도 해당 값이 만약 1,000,000,008 이라면 이 역시 int 자료형에 제대로 담길 수 없다.
따라서 이 과정에서 dp[i-1] + dp[i-2] + dp[i-3] 값을 long long 형 임시 변수에 담고 이 값을 1,000,000,009 로 나눈 나머지를 dp 배열에 담아주는 방법을 사용했다!!
혹은 dp 배열 자체를 long long 형으로 만들어 줘도 안전할 것 같다!
코드
#include <iostream>
#include <vector>
// BOJ 15988 1,2,3 더하기 3 / DP / 실버 2
using namespace std;
int getDP(int num){
vector<int> dp(num+1, 0);
dp[0] = 1;
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
if (num>=4){
for (int i = 4; i <= num ; ++i) {
long long sum = 0;
for (int j = 1; j <= 3 ; ++j) {
if (i-j >= 0){
sum += dp[i-j];
} else break;
}
dp[i] = sum % 1000000009;
}
}
return dp[num];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, num;
cin>>N;
for (int i = 0; i < N; ++i) {
cin>>num;
cout<<getDP(num)<<'\n';
}
return 0;
}