[알고리즘 풀이 분석] BOJ 21317 징검다리 건너기

오늘 풀어본 문제는 BOJ 21317 징검다리 건너기 이다!
DP를 이용해서 풀었고 난이도는 실버 1에 해당한다!

BOJ 21317 징검다리 건너기

심마니 영재는 산삼을 찾아다닌다.

산삼을 찾던 영재는 N개의 돌이 일렬로 나열되어 있는 강가를 발견했고, 마지막 돌 틈 사이에 산삼이 있다는 사실을 알게 되었다.

마지막 돌 틈 사이에 있는 산삼을 캐기 위해 영재는 돌과 돌 사이를 점프하면서 이동하며 점프의 종류는 3가지가 있다.

점프의 종류에는 현재 위치에서 다음 돌로 이동하는 작은 점프, 1개의 돌을 건너뛰어 이동하는 큰 점프, 2개의 돌을 건너뛰어 이동하는 매우 큰 점프가 있다.

각 점프를 할 때는 에너지를 소비하는데, 이 때 작은 점프와 큰 점프시 소비되는 에너지는 점프를 하는 돌의 번호마다 다르다.

매우 큰 점프는 단 한 번의 기회가 주어지는데, 이때는 점프를 하는 돌의 번호와 상관없이 k만큼의 에너지를 소비한다.

에너지를 최대한 아껴야 하는 영재가 산삼을 얻기 위해 필요한 에너지의 최솟값을 구하여라.

영재는 첫 번째 돌에서부터 출발한다.

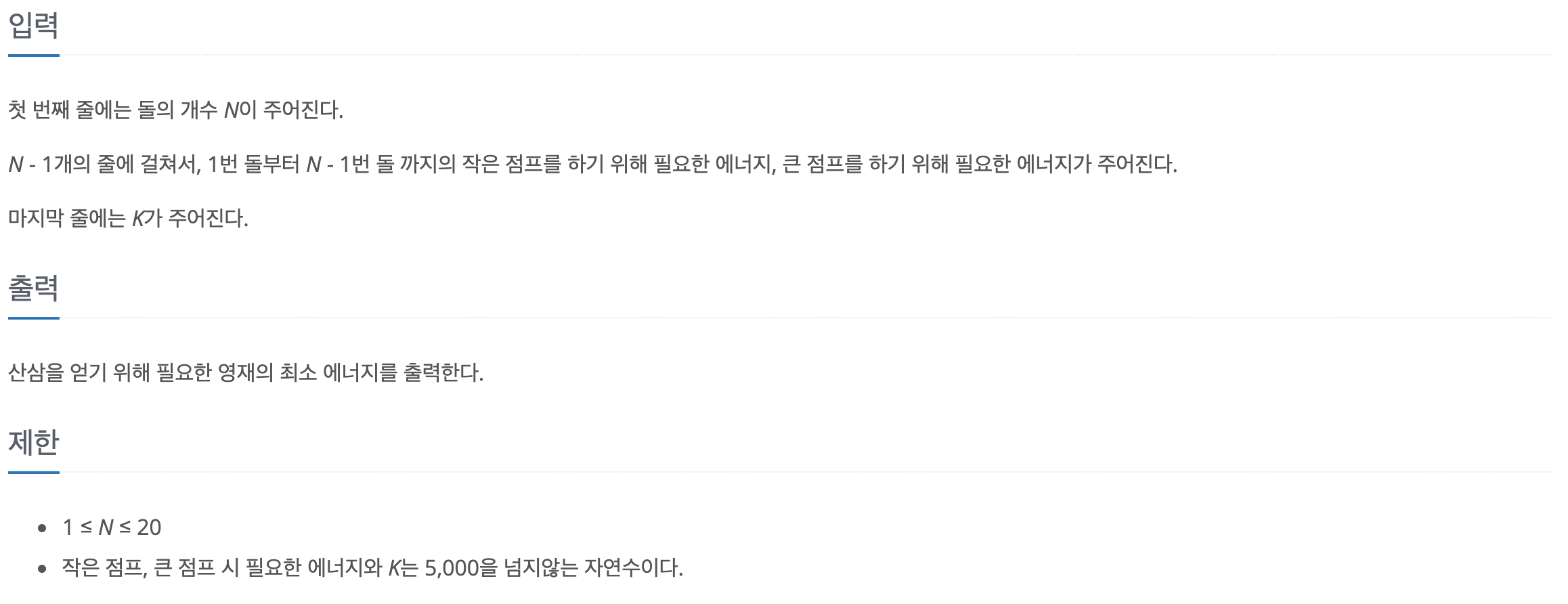
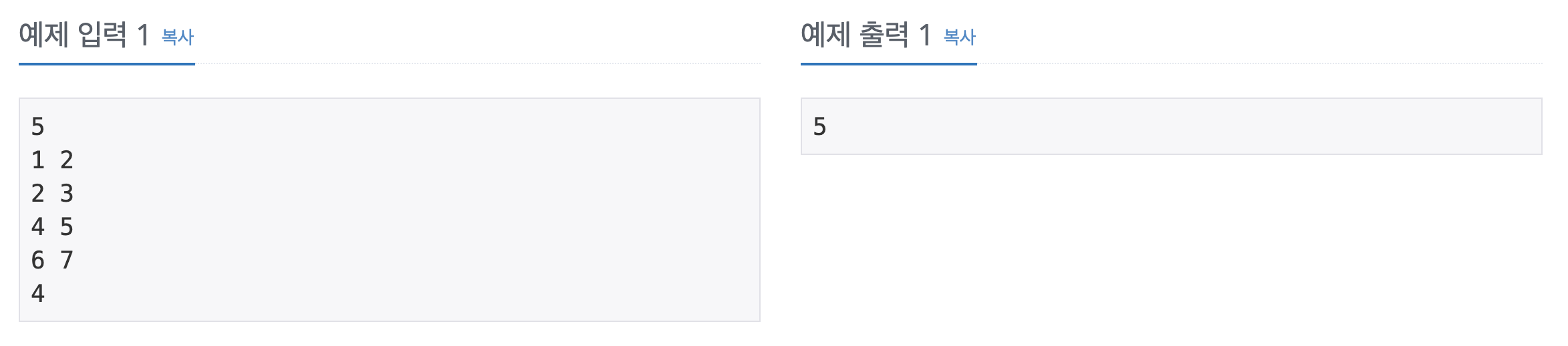
입출력

나의 풀이

내가 처음으로 시도했던 풀이에서 2차원 배열 dp[i][0], dp[i][1] 에 담기는 값의 의미는

• dp[i][0] : 매우 큰 점프를 사용하지 않고 i번째 돌에 오는 최소 에너지
• dp[i][1] : 매우 큰 점프를 한번 사용하여 i번째 돌에 오는 최소 에너지

이다.

i번째 돌을 기준으로 하고 i-1, i-2, i-3번째 돌에서 오는 에너지의 최소 값을 계산해 dp 배열을 갱신해 주는 방식으로 작성하였다.

하지만 주어진 예시도 하나밖에 없었고 지속적으로 채점을 시작하자마자 '틀렸습니다' 가 떴는데,, 문제가 올라온지 얼마 안된 것 같다 ㅜ 질문도 하나밖에 없고,, 테스트 케이스도 내가 만들어 적용해 봐도 통과하지 못하기에 방법을 조금 바꿔보았다.

i번째 돌을 기준으로 할 때 i번째 돌까지 오는 경우를 따지지 말고, i번째 돌에서 출발하는 경우를 생각하는 방식이다. 예를 들어 5개의 돌 중 2번째 돌 위에 있다면

• 2번째 돌에서 작은 점프를 하는 경우 -> 3번째 돌
• 2번째 돌에서 큰 점프를 하는 경우 -> 4번째 돌
• 2번째 돌에서 매우 큰 점프를 하는 경우 -> 5번째 돌

의 세가지 경우를 생각하고 dp 배열의 2번째 index는 0(매우 큰 점프를 사용하지 않은 경우), 1(매우 큰 점프를 사용한 경우) 를 의미 한다.

아와 같은 방식으로 i = 1~N-1까지 진행하고 i+1, i+2, i+3 이 주어진 범위 N을 넘지 않는지 체크해주며 구현해 주었다.

결과 값은 dp[N][0], dp[N][1] 중 더 작은 값을 반환한다.

의문점❓

이 방식으로 된 풀이가 통과는 했지만 한가지 마음에 걸리는 부분이 있다 ㅜ
통과된 풀이 방식으로 코드를 작성하고 문제에 함께 제공된 테스트 케이스를 기준으로 하면,

• i=1 일 때
  초기 값으로 dp[1][1] = 0이고,
  dp[i + 1][1] = min(dp[i + 1][1], dp[i][1] + energy[i].first) 과
  dp[i+2][1] = min(dp[i+2][1], dp[i][1] + energy[i].second)
  에 의해서 dp[2][1], dp[3][1] 의 값이 각각 1, 2 로 갱신된다.

그런데 정한바에 의하면 dp[2][1], dp[3][1]은 각각 매우 큰 점프를 사용했을 때 사용되는 에너지 값이다.

하지만 2,3번째 돌에 오기 전에는 매우 큰 점프를 사용할 수 없지 않은가,,?

때문에 나는 첫번째 풀이 방식을 사용했을 때 dp[1][1], dp[2][1], dp[3][1] 값을 모두 초기 값으로 설정했었다.

물론 i=4일 때 부터는 dp[5][1](1->4->5), dp[6][1](1->4->6) 의 경우를 대비 하기 위해 일괄적으로 선택된 방법이지만,,

음,, 이것때문에 첫번째 풀이 방법이 통과하지 못했던 것인지, 문제 조건에서 '1, 2,3번째 돌까지는 매우 큰 점프를 사용할 수 없다' 의 조건이 없기 때문에 상관이 없는지,, 는 조금 의문 스럽다,,!

혹시라도 누가 이 글을 본다면 의견을 남겨주면 좋겠다 ㅎㅎ

코드

#include <iostream>
#include <vector>

// BOJ 21317 징검다리 건너기, DP, 실버 1
using namespace std;

int getMinEnergy(vector<pair<int, int>> energy, int N, int K){
    vector<vector<int>> dp(N+1, vector<int>(2, 2147483647));
    dp[1][0] = 0;
    dp[1][1] = 0;

    for (int i = 1; i<=N-1 ; ++i) {
        if (i + 1 <= N) {
            dp[i + 1][0] = min(dp[i + 1][0], dp[i][0] + energy[i].first);
            dp[i + 1][1] = min(dp[i + 1][1], dp[i][1] + energy[i].first);
        }

        if (i + 2 <= N) {
            dp[i+2][0] = min(dp[i+2][0], dp[i][0] + energy[i].second);
            dp[i+2][1] = min(dp[i+2][1], dp[i][1] + energy[i].second);
        }

        if (i + 3 <= N){
            dp[i+3][1] = min(dp[i+3][1], dp[i][0] + K);
        }
    }

    return min(dp[N][0], dp[N][1]);
}


int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N, K;
    cin>>N;

    if (N==1){
        cin>>K;
        cout<<0;
    }
    else{
        vector<pair<int, int>> energy(N);
        for (int i = 1; i < N; ++i) {
            cin>>energy[i].first>>energy[i].second;
        }
        cin>>K;

        int minEnergy = getMinEnergy(energy, N, K);
        cout<<minEnergy;
    }

    return 0;
}