본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 꼭 댓글 남겨주세요.
오차역전파 Backpropagation
오차역전파는 말 그대로 오차(error)를 거꾸로 전파(backpropagation)하는 방법입니다. 여기서 오차란 모델의 예측값과 실제값의 차이를 말합니다. 보통은 와 같이 표현하고, 구체적인 오차의 값은 loss function을 통해 계산합니다.
오차를 구하면 그 다음엔 뭘 하나요?
오차는 우리가 실제 함수를 모르기 때문에 발생합니다.
예를 들어 오늘 습도가 78%일 때 내일 비가 올 확률을 100% 정확하게 알 수 있다면 굳이 머신러닝이 필요하지 않습니다. 하지만 우리는 오늘의 습도와 내일의 강수확률의 상관관계를 모릅니다. 그래서 이를 근사하는 함수를 만들고, 이를 모델이라 부릅니다.
그런데 과연 강수확률이 습도에만 영향을 받을까요? 당연히 그렇지 않습니다. 강수확률에 영향을 미치는 다양한 변수가 존재합니다. 그래서 우리가 만든 모델은 필연적으로 여러 변수가 존재하는 다변수함수의 형태를 갖게 됩니다. 만약 각 변수가 결과에 미치는 영향력을 알 수 있다면 함수를 더 정확하게 근사할 수 있습니다.
경사하강법과 오차역전파
각 변수를 조금씩 바꿔보면서, 결과가 어떻게 바뀌는지 살펴보자!
모델(다변수함수)의 계수를 구하기 위해 사용하는 방법이 바로 경사하강법입니다. 어떤 변수의 계수, 즉 가중치를 바꿨는데 오차가 줄어든다면 이는 이전보다 더 정확한 함수를 찾은 것과 같습니다. 그러니 올바른 방향으로 가중치를 계속 갱신한다면 언젠가는 최적점에 도달하게 되겠죠.
그런데 이 가중치를 직접 계산하려면 전체 방정식을 알아야 하지만 우리는 모델이 명시적으로 어떻게 표현되는지 모릅니다. 설사 안다고 해도 변수 개수가 수백, 수천만개를 넘어 수십 수백억개인데 그걸 다 일일이 계산하는 건 매우 비효율적입니다.
이 때 오차역전파를 이용하면 간단하고 효율적으로 계산할 수 있습니다.
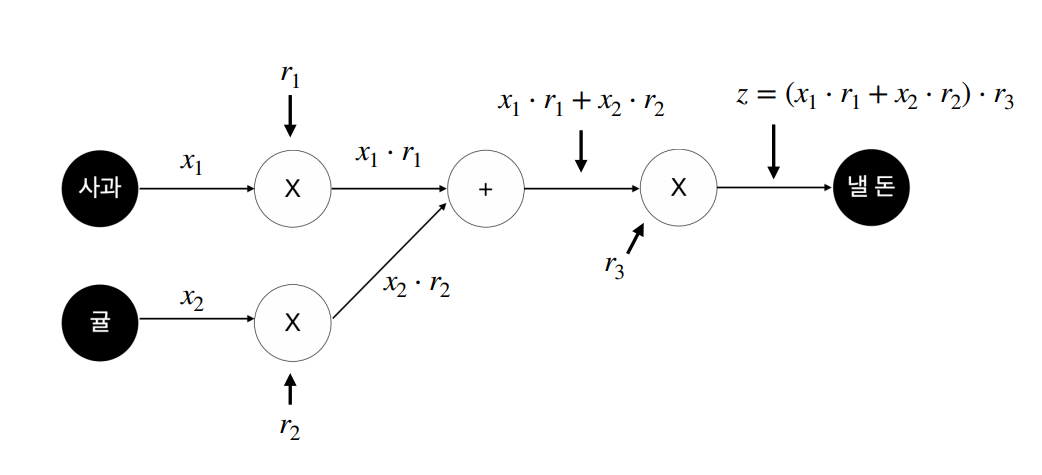
예를 들어서 위와 같은 모델이 있다고 가정해 봅시다. 위 그림에서 우리가 계산해야 하는 각 변수의 영향력은 입니다. Loss function 라고 하면 우리가 계산해야 하는 것들은 아래와 같습니다.
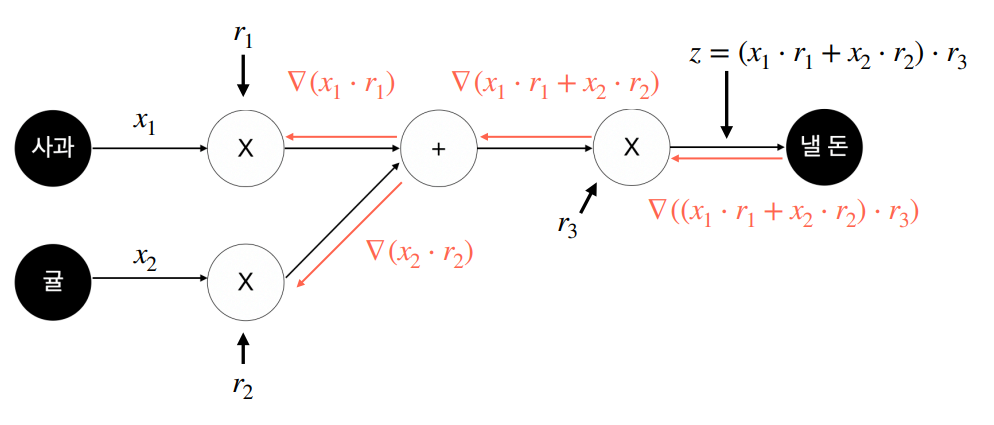
위 그림은 변수가 3개밖에 없지만 변수 숫자가 20개만 되어도 수식이 엄청나게 복잡해질 것입니다. 그래서 다음 그림처럼 간단한 트릭을 사용합니다.

바로 개별 연산을 각각의 함수로 취급하는 것입니다. 그러면 loss function을 하나의 합성함수로 표현할 수 있게 됩니다. 그러면 합성함수의 미분법, 즉 연쇄법칙(chain rule)을 사용해서 복잡했던 미분 계산을 다음과 같이 간단하게 표현할 수 있습니다.
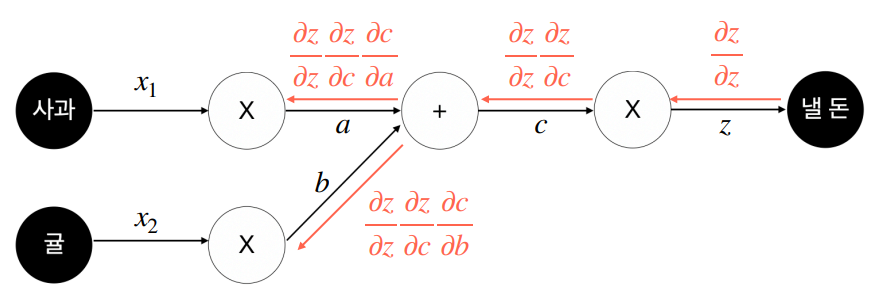
위 그림에서 붉은 화살표를 보면 순전파와는 반대 방향으로 계산이 전달됩니다. 그런데 왜 바로 각 노드를 계산하지 않고 거꾸로 거슬러 올라가면서 계산을 해야 할까요?
정답은 각각의 함수가 이전 노드의 출력에 종속되기 때문입니다. 즉, 이전 노드의 출력이 바뀌면 각각의 함수값도 바뀌게 됩니다. 따라서 오차역전파법을 사용하려면 결과적으로 계산에 관여하는 모든 노드의 함수값을 알고 있어야 합니다. 컴퓨터 입장에서는 이 수많은 함수값을 전부 메모리에 올려야 한다는 뜻입니다. 당연하지만 올려놓은 변수들에 대해 연산도 해야 하니까 메모리 사용량은 몇 배로 증가합니다. 만약 변수 개수가 수십억개라면 메모리가 엄청나게 필요하겠죠.
오차역전파의 계산은 다음과 같이 이루어집니다.
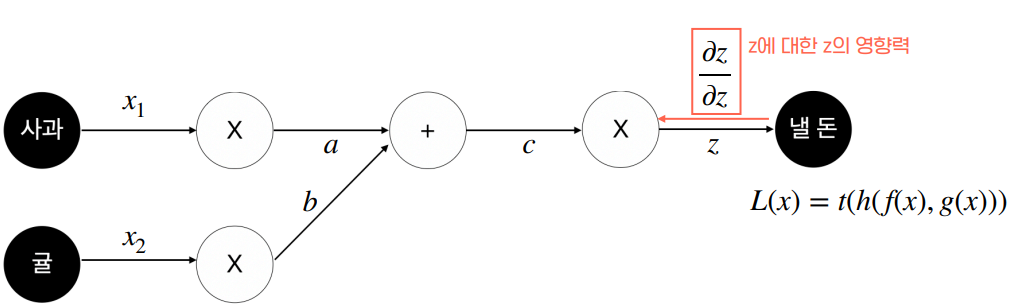
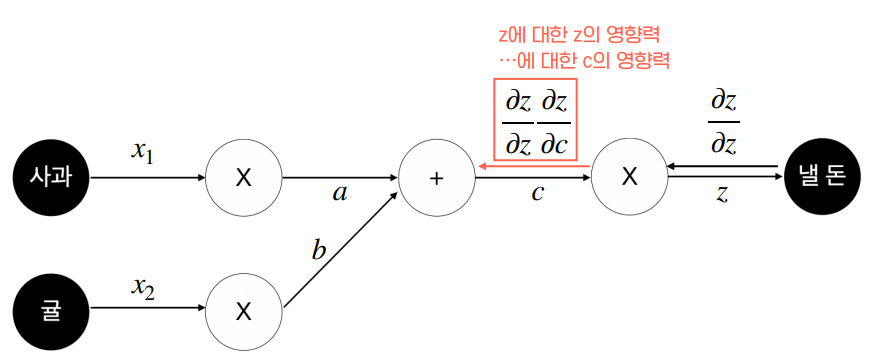
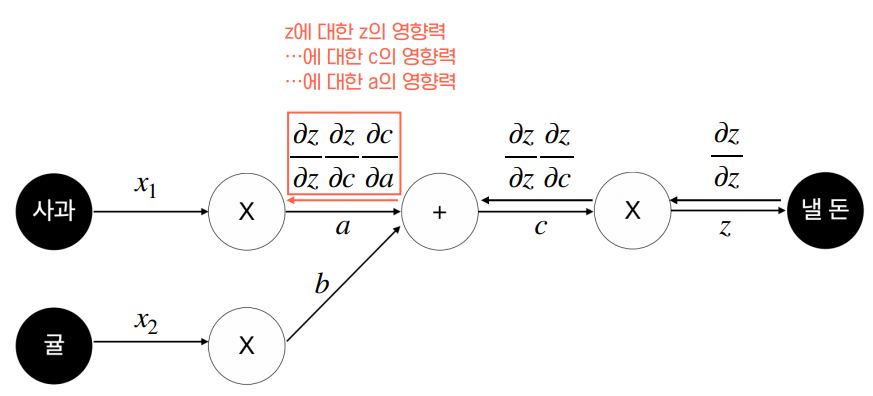
이상의 과정을 거쳐 최종적으로는 다음 그림과 같은 형태가 됩니다.
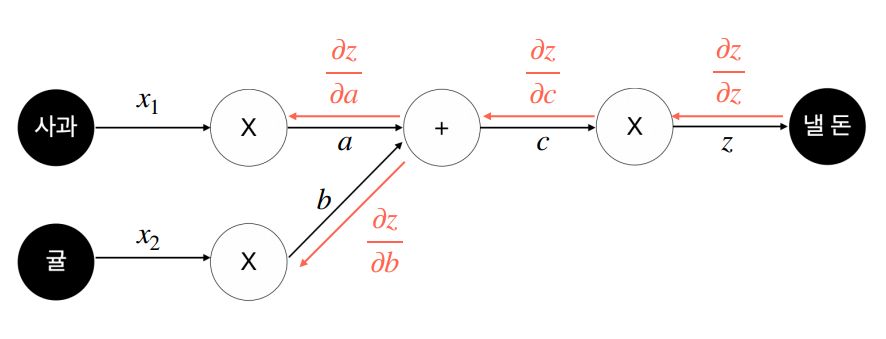
결과적으로 직접 방정식을 대입해서 풀지 않고도 계수를 계산할 수 있게 됩니다.
참고문헌
