[딥러닝] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Papers Review

Published in PMLR 2015
요약
-
Network 내부에서 layer마다 input 분포가 달라지는 Internal Covariate Shift 발생
- 수렴 속도를 감소시키고 학습을 불안정하게 함 -
이를 해결하기 위해 Batch Normalization을 제안
- 각 batch의 통계량을 이용하여 layer 내부 node마다 normalize를 수행
서론
Abstract
DNN을 학습시킬 때, SGD 기반의 방법론을 쓰면 각 레이어별로 입력의 분포가 변화합니다. 결과적으로 내부 input feature의 분포가 계속 변하는 Internal Covariate Shift (내부 공변량 변화, ICS) 문제가 발생합니다. 즉, train을 통해 찾아내는 feature 분포와 실제 test dataset의 feature 분포가 서로 달라지게 됩니다.
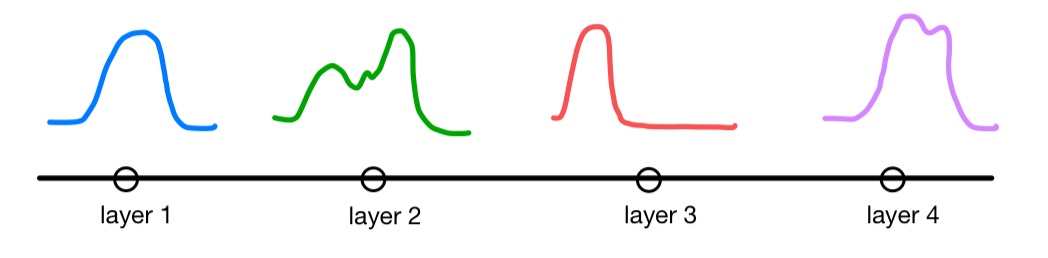
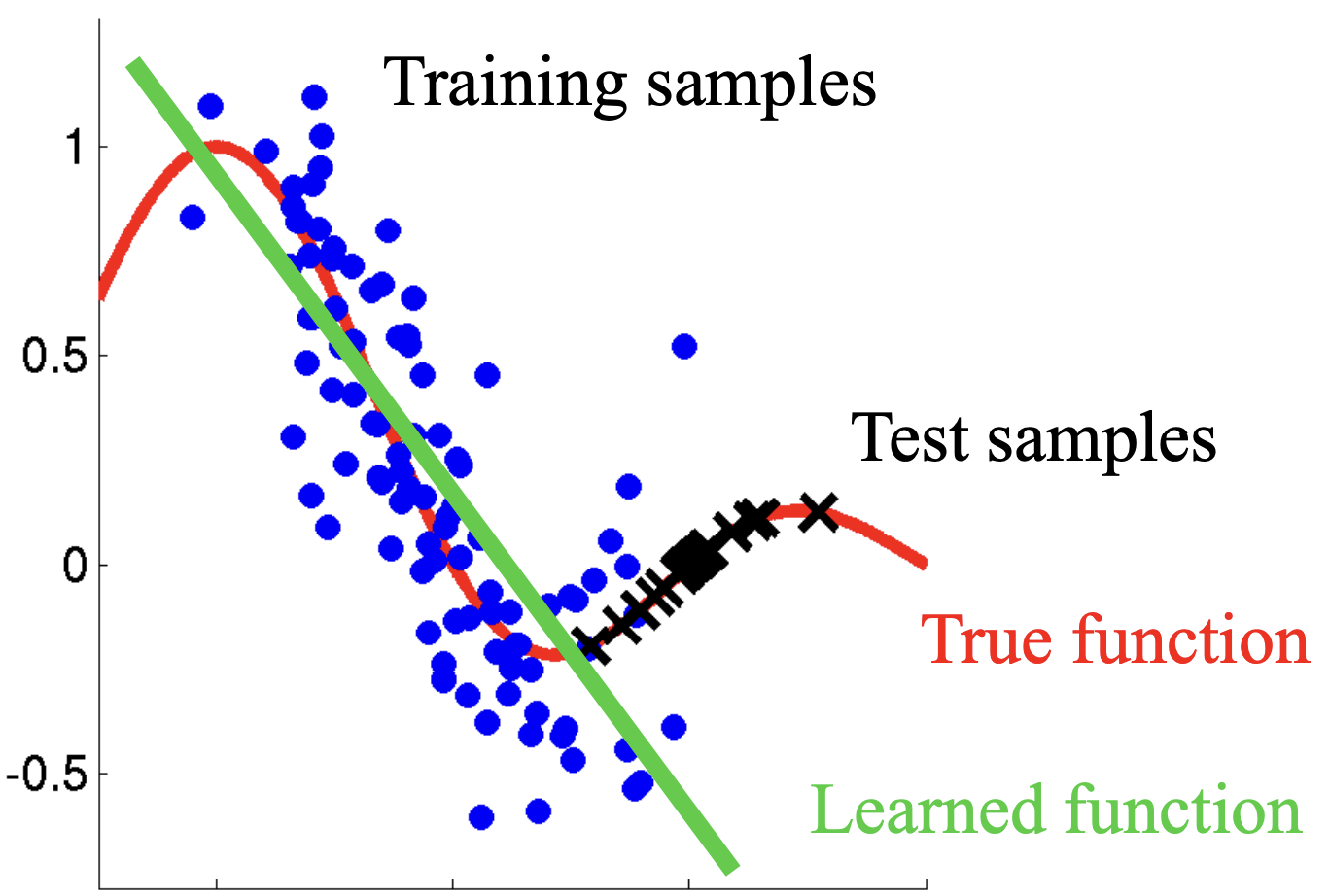
직관적으로 보자면 학습 과정에서 각 레이어가 근사하는 feature function이 위와 같이 다양하게 변하면서...
위 그림처럼 true function을 제대로 근사하지 못하게 되는 것을 말합니다.
본 논문은 이를 해결하기 위해 Batch Normalization 이라는 방법을 제안합니다.
1. Introduction
SGD를 사용하는 DNN은 다음과 같이 파라미터 를 최적화하는 것이 목표입니다.
SGD를 사용하여 학습할 때, 각 레이어는 이전 레이어의 출력에 영향을 받습니다. 예를 들어, 하나의 딥러닝 모델은 sub network (layer) 를 통해 다음과 같이 나타낼 수 있습니다.
여기서 라고 하면,
가 됩니다. 이 모델의 파라미터 업데이트는 다음과 같이 이루어집니다.
즉, 전체 모델은 를 입력받는 sub network와 같습니다. 논문에서는 이 때 의 분포를 어느 정도 고정해주는 것이 안정적인 수렴에 도움을 준다고 주장합니다. 각각의 레이어는 이전 레이어에 영향을 받으므로, input 의 분포가 크게 변하지 않으면 를 안정적으로 학습할 수 있다는 논지입니다.
본론
2. Towards Reducing Internal Covariate Shift
저자들이 처음에 시도한 것은 training step마다 activation을 whitening하는 것이었는데, 이는 수렴 과정에서 gradient descent가 제대로 이뤄지지 않는 문제가 있었습니다. 예를 들어 input 와 bias 를 갖는 레이어에 대해 activation의 평균을 가지고 normalization을 진행하는 과정은 다음과 같이 나타낼 수 있습니다.
이 때 gradient descent를 통해 bias 는 다음과 같이 업데이트됩니다.
따라서 normalization 이후 레이어의 출력은 다음과 같습니다.
즉, normalization이 출력에 아무런 영향을 끼치지 못합니다. 오차역전파 과정에서 BN의 효과가 반영되지 않는 것입니다. 논문에서는 이 문제를 해결하기 위해 모든 input data에 대해 출력된 activation이 정해진 distribution을 따르는 normalization 함수 을 가정합니다. 이렇게 하면 gradient descent로 loss를 계산할 때 normalization 연산의 영향력을 포함시킬 수 있게 됩니다. 를 layer의 input vector, 를 전체 데이터에서 생성될 수 있는 모든 input vector라고 하면 다음과 같이 나타낼 수 있습니다.
이제 위 식을 미분하면 되는데, 은 다변수함수이기 때문에 Jacobian 행렬 을 계산해야 합니다. 즉, 와 를 계산해야 하므로 연산량이 지나치게 증가하게 됩니다.
3. Normalization via Mini-Batch Statistics
모든 layer의 입출력을 개별적으로 whitening하는 작업은 위와 같이 많은 cost를 요구합니다. 그래서 논문에서는 2가지 방법으로 정규화 과정을 간소화합니다.
- input data 의 각 dimension에 대해 정규화 수행
- 각 batch의 mean, variance를 통해 모평균/분산을 추정
개의 차원을 가진 input 에 대해 normalized result 는 다음과 같습니다.
그런데 이렇게 를 whitening하면 각 layer의 representation이 변형될 수 있습니다. 예를 들어, 다음과 같이 sigmoid function을 활성화 함수로 사용할 경우 output 가 붉은색으로 표시된 linear regime에 분포하게 되므로 해당 레이어를 기점으로 네트워크는 nonlinearity를 잃게 됩니다.
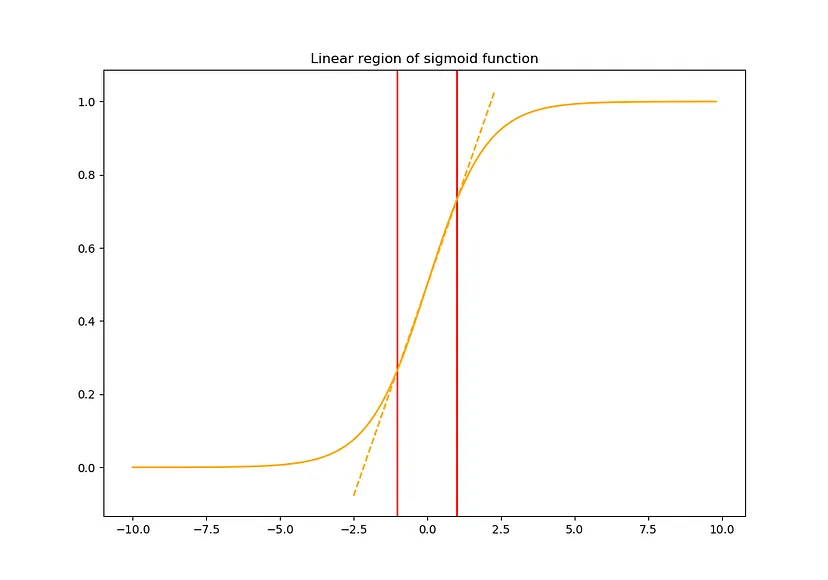
그래서 다음과 같이 transformation 과정에서 nonlinearity를 가지도록 조정해줍니다.
는 모두 learnable parameter이고 경우에 따라 일 수도 있습니다. 어쨌든 목적은 각 layer의 representation이 달라지지 않도록 scaling & shifting하는 것입니다.

BN 알고리즘을 보면 등의 통계값은 batch 구성에 따라 값이 변할 수 있습니다. 결과적으로 각각의 레이어는 정규화된 값 를 scaling & shifting한 를 입력으로 받게 됩니다. 또한 다음과 같이 네트워크의 loss function을 각각의 파라미터에 대해 미분할 수 있으므로 모든 파라미터는 학습가능합니다.
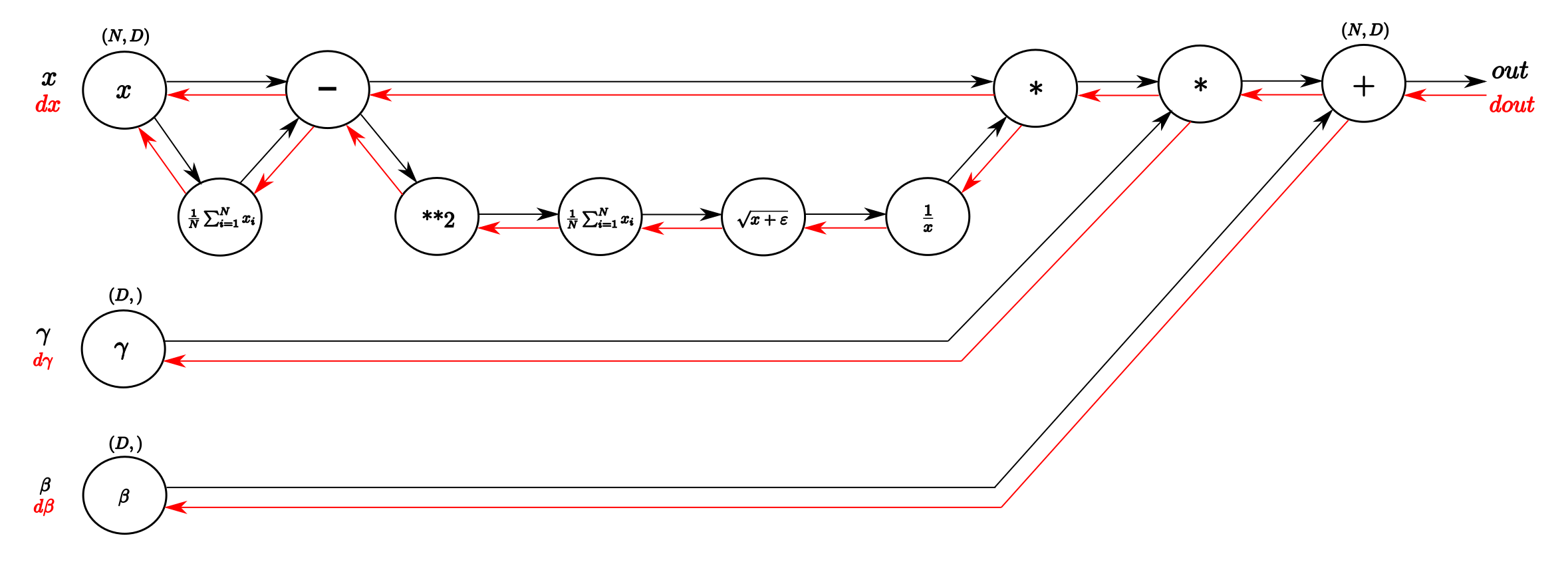
각 파라미터를 계산 그래프로 나타내면 위와 같습니다.
Batch Normalizaiton과 Internal Covariate Shift 완화
BN은 기본적으로 데이터를 scaling & shifting 하는 변환입니다. 같은 모양의 distribution이지만, activation이 더 안정적으로 활성화되는 region으로 분포를 옮기는 것이죠. 그런데 이 말은 다르게 표현하면 레이어가 입력받는 데이터 분포가 한정될 수 있다는 의미도 됩니다. 즉, scaling & shifting 된 데이터 분포가 target function을 충분히 대표하지 못하는 상황이 발생할 가능성이 있습니다.
실제로 Batch Normalization과 ICS에 대해서는 아직도 여러 논의와 연구가 이루어지고 있습니다. 예를 들어 How does batch normalization help optimization? (2018, NIPS) 라는 논문에 따르면 BN은 오히려 ICS를 증가시킵니다. BN이 학습을 안정화시키는 것은 맞지만, 논문에서 주장하는 바와 같이 ICS 문제를 해결함으로써 optimization에 기여하는 것은 아닙니다.
참고문헌