Published in NeurIPS 2022 | Implementation

2022년 12월에 arxiv에 올라온 힌튼의 따끈따끈한(?) 논문입니다.

Backpropagation의 대안이 될 가능성이 있는 알고리즘이라고 하는데, 개인적으로 힌튼의 깔끔하고 읽기 편하면서도 흥미를 유발하는 글쓰기 스타일을 좋아하는 편이라 벌써부터 무슨 내용일지 기대가 되네요.

---

[요약]

Backpropagation의 대체재가 될 수 있는 Forward-Forward (FF) 알고리즘을 제안했습니다. FF 알고리즘은 Backward 연산 대신 2개의 Forward pass로 구성됩니다. 각각 Positive / Negative pass라고 부릅니다.

Positive pass는 Real data에 최적화되는 것을 목표로 하고, Negative pass는 False data에서 최대한 멀어지는 것을 목표로 합니다.

---

[서론]

0. Abstract

Forward-Forward 알고리즘은 backpropagation의 forward-backward 과정을 2개의 Forward pass로 대체하는 알고리즘입니다.

2개의 Forward pass가 있는데, 하나는 Positive 값을 전파하고 다른 하나는 Negative 값을 전달합니다. 각각의 pass는 Positive에는 가까워지고, Negative에서는 멀어지는 것을 목표로 학습합니다.

1. What is wrong with the Backpropagation

힌튼이 대뇌 피질의 학습 과정에 대한 이야기를 하는 부분이 있는데, FF 알고리즘을 이해하는데 도움이 될 것 같아서 조금 짚고 넘어가겠습니다.

The top-down connections from one cortical area to an area that is earlier in the visual pathway do not mirror the bottom-up connections as would be expected if backpropagation was being used in the visual system. Instead, they form loops in which neural activity goes through about half a dozen cortical layers in the two areas before arriving back where it started.

진짜로 뇌가 오차역전파와 같은 방식으로 학습한다면 있어야 하는 backward pass는 실제로 존재하지 않고, 대신 시냅스의 처음으로 돌아가기 전에 cortical layer를 지나는 과정에서 모종의 루프를 형성한다 는 내용입니다.

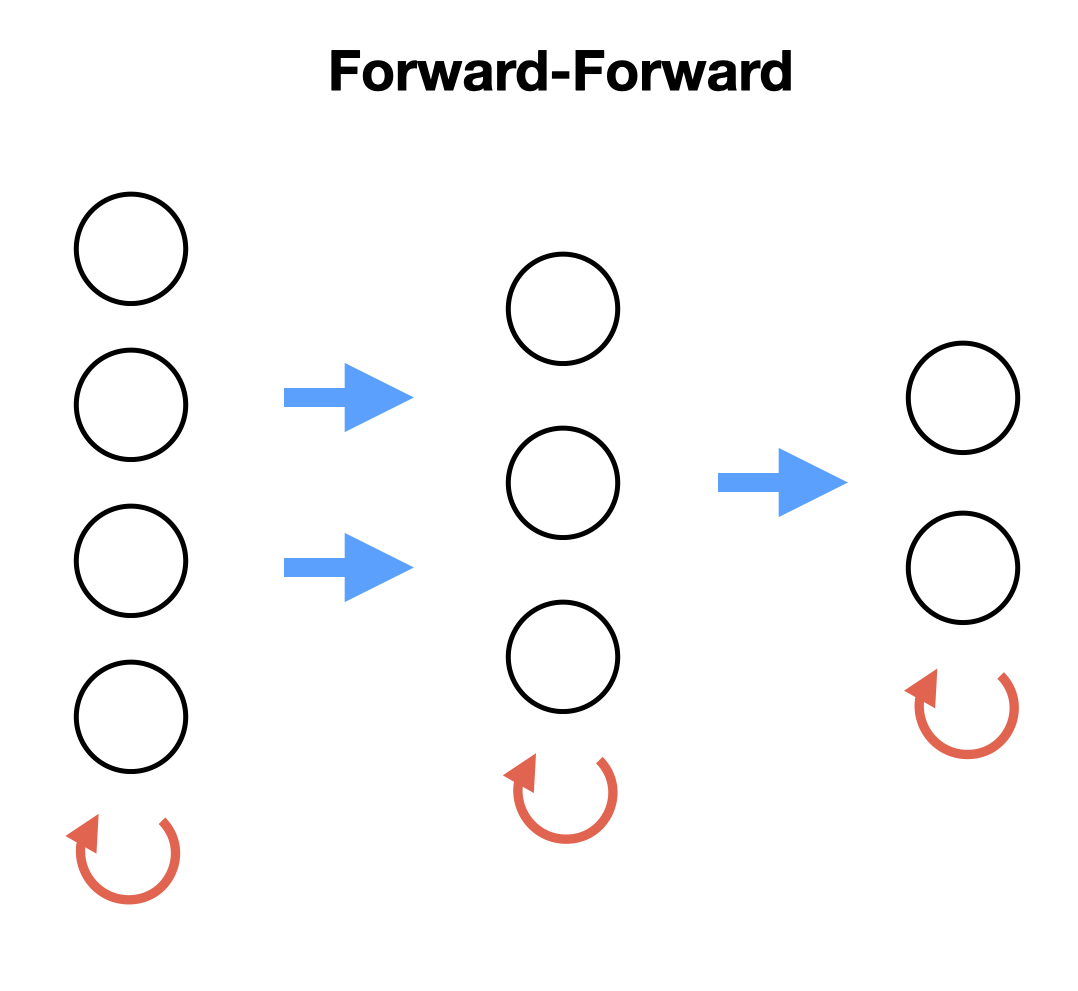
아래에서 살펴보겠지만, Forward-Forward 방식은 위와 같이 Unit(layer) 단위로 Local Update가 진행됩니다.

[본론]

2. The Forward-Forward Algorithm

저자는 볼츠만 머신과 Noise Contrastive Estimation에서 FF 알고리즘의 모티브를 따왔다고 합니다.

두 forward pass는 동일한 방식으로 작동합니다. 차이점이라면 하나는 positive data에 최적화되고, 다른 하나는 negative data에서 최대한 멀어지는 학습을 진행한다는 것입니다.

예를 들어 학습에 SSE(sum of squared)를 사용한다면, input vector가 positive data일 확률 $p(positive)$는 다음과 같습니다.

$\sigma=$ logistic function
$\theta=$ threshold (상수값)
$y=$ layer norm을 하지 않은, 이전 레이어에서 넘겨받은 output
$y_j=$ $y$의 $j$번째 unit (스칼라 or 벡터)
$(\sum_jy_j^2-\theta) =$ goodness (적합도)
$\quad$

즉, goodness의 값을 보고 positive인지 negative인지 판정하게 됩니다.

2.1 Learning multiple layers of representation with a simple layer-wise goodness function

한 개의 레이어를 최적화하는 데에는 위에서 살펴본 방식으로도 별 문제가 없습니다. 그런데 여러 개의 레이어를 거쳐야 하는 경우, 이전 레이어의 activation vector를 넘겨 받았을 때 이게 positive인지 negative인지 매우 쉽게 구분할 수 있습니다. positive / negative pass 시에 전달되는 activation vector의 길이가 다르기 때문입니다. 결과적으로 더 이상의 feature 학습이 일어나지 않게 됩니다.

논문에서는 이 문제를 해결하기 위해 레이어 단위로 activation vector의 길이를 normalize 해 줍니다.

3. Some experiments with FF

3.1 The backpropagation baseline

논문에서는 MNIST 데이터셋 위주로 실험했습니다. Backpropagation를 사용하는 잘 설계된 CNN이 평균 0.6% 정도의 오차를 보이는데, FF를 사용했을 때는 약 1.4% 정도의 오차를 기록했습니다. 기존에 제안되었던 backprop의 다른 대체재들이 2% 이상의 오차를 보이는 것에 비교하면 꽤 괜찮은 성능을 보여주는 셈입니다.

3.2 A simple unsupervised example of FF

FF를 사용할 때 고려해야 하는 점은 크게 2가지가 있습니다.

(1) 좋은 negative data를 사용하면 좋은 representation을 얻을 수 있는가?

(2) 좋은 negative data란 무엇이며, 어떻게 얻을 것인가?

참고로 본 논문에서는 직접 negative data를 만들어서 학습에 사용했습니다.

지도학습에서 Contrastive Learning 기법을 사용할 때는, 먼저 별도의 label 정보 없이 입력 벡터를 representation vector로 변환합니다. 이후 변환된 벡터들을 간단한 linear transform을 통해 logit으로 바꾸고, softmax에 넣어서 각 label에 대한 확률값을 얻는 구조로 되어 있습니다.

위에서 선형변환을 통해 logit을 얻는 과정에는 backprop이 필요 없습니다. 그냥 간단한 지도학습이죠. [a, b, c, d] 라는 벡터를 주고 [3] 값이 나오도록 변환하는 가중치 행렬을 구하기만 하면 되니까요.

FF는 real vector를 positive example로 주고, false vector를 negative example로 주어서 간단한 지도학습을 시킨다는 점에서 이와 유사한 학습 방식이라고 할 수 있습니다.

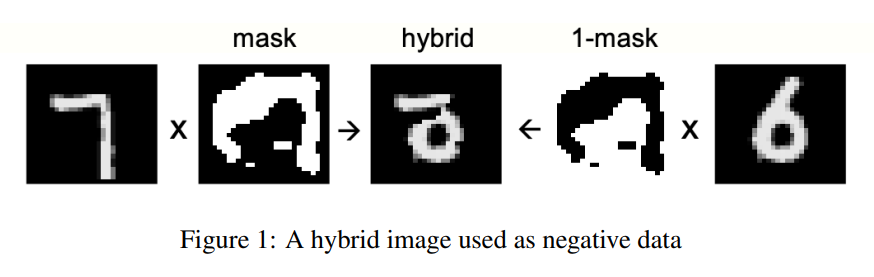
논문에서는 False data를 위와 같은 방식으로 직접 만들어서 넣어주었습니다.

(1) 먼저 positive data에 0과 1로 구성된 임의의 마스크를 만들어서 각 픽셀끼리 곱합니다.

(2) (1-mask) 값을 갖는 반전된 마스크를 만들어서 negative data에 곱합니다.

(3) 두 데이터를 더해서 hybrid image를 생성합니다.

4개의 FC 레이어로 구성된 네트워크로 100 epoch 학습 결과, 1.37%의 에러율을 보였다고 합니다. 단, 이는 마지막 3개 레이어의 출력값(activity vector)들을 normalize해서 softmax에 입력했을 때의 결과고, 첫 레이어의 출력을 나머지 3개 레이어에 입력으로 넣었을 때는 오히려 성능이 저하되었다고 하네요.

또, FC layer를 쓰는 대신 가중치를 공유하지 않는 local receptive field도 (=CNN) 사용해봤는데 성능이 향상되었다고 합니다. 60 epoch 학습 후에 1.16%의 오차를 보였고, 균등한 네트워크 활성화를 위해 peer normalization을 사용했습니다.

3.3 A simple supervised example of FF

Unsupervised case처럼 복잡한 마스킹이 필요 없습니다. label 정보를 각각 입력값에 추가해주면 됩니다.

구체적으로는 positive data에는 정답 레이블을 주고, negative data에는 오답 레이블을 줍니다. 이 경우, 두 data의 차이는 오직 레이블이기 때문에 추론에 필요 없는 feature를 무시하게 됩니다.

MNIST의 경우, Convolution 처리를 용이하게 할 수 있도록 검은색 경계선을 가지고 있습니다. 첫 10개의 픽셀값을 각 label의 one hot vector로 바꿔주면, 첫 레이어가 뭘 배우고 있는지 쉽게 확인할 수 있습니다.

학습이 끝나고 inference 시에는 값을 전부 0.1로 초기화한 one hot label vector를 붙여서 넣어주면 된다고 합니다. 논문에서는 학습한 네트워크에서 첫 번째 레이어를 제외한 나머지 3개 레이어의 active vector를 softmax에 넣으면 바로 추론이 가능하다고 하는데요.

이 방법이 전체 네트워크를 거치는 것보다 빠르긴 하나, 어디까지나 편법이고 정확도도 떨어지기 때문에 그냥 각 레이블별로 한 번씩 학습을 돌려서 최적화시켜주는 게 좋다고 합니다. 즉, 레이블 개수만큼 inference 하는 작업이 필요합니다.

실험 결과 4개의 FC layer로 구성된 FF 네트워크는 60 epoch 후 약 1.36%의 오차율을 보였으며, Backprop을 사용했을 때에는 20 epoch만에 비슷한 성능에 도달했다고 합니다. learning rate를 2배로 늘려주었을 때는 40 epoch만에 약간 낮은 1.46% 오차율을 기록했다고 하네요.

3.4 Using FF to model top-down effects in perception

지금까지 논문에서 살펴본 feed-forward 기반 방식은 한 번에 레이어 한 개씩만을 최적화합니다. backprop을 사용하지 않기 때문에 나중 레이어에서 학습한 내용을 가지고 이전 레이어를 업데이트할 수가 없습니다.

그래서 논문에서는 이미지를 비디오처럼 처리하는 방식을 택합니다. 동일한 이미지가 계속해서 반복되는 영상 데이터를 다룬다고 생각하면 이해가 쉽습니다.

기본적인 네트워크 구조는 저자가 발표했던 Multi layer RNN과 비슷합니다.

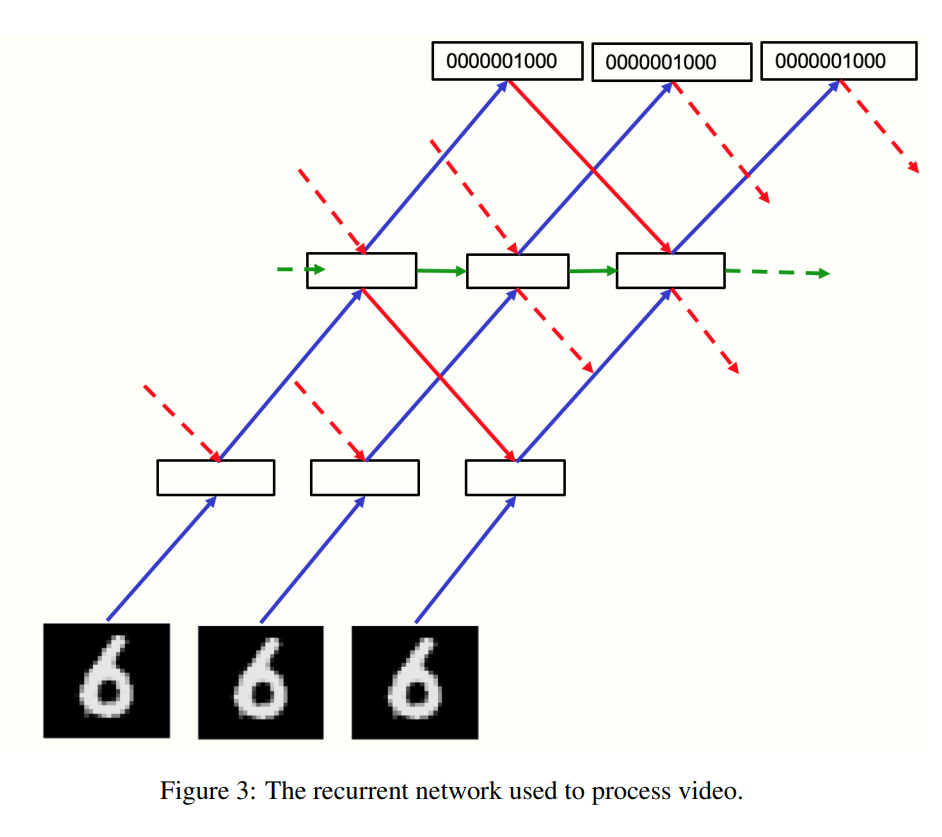
가장 밑에 위치한 bottom layer는 pixel image를 입력으로 받고, 맨 위에 위치한 top layer는 각 클래스의 one hot vector를 입력으로 받습니다. 위 그림에서 파란색 화살표가 positive pass, 빨간색 화살표가 negative pass 입니다.

각각의 positive / negative pass는 동시에 흐르지만, 각 레이어의 activation vector는 바로 이전 time step의 위/아래 레이어의 normalized activity vector에 의해 결정됩니다.

각 pass의 흐름을 보면 $F_t$ 레이어는 $P(t-1)$와 $F(t-1)$ 값을 전달받고 있습니다. 논문에서는 넘겨받은 pre-normalized state 값에 0.3을 곱하고, 새로 계산한 state 값에 0.7을 곱해서 더하는 방법으로 가중치를 업데이트했다고 합니다. 식으로 나타내면 다음과 같이 되겠지요.

4 Experiments with CIFAR-10

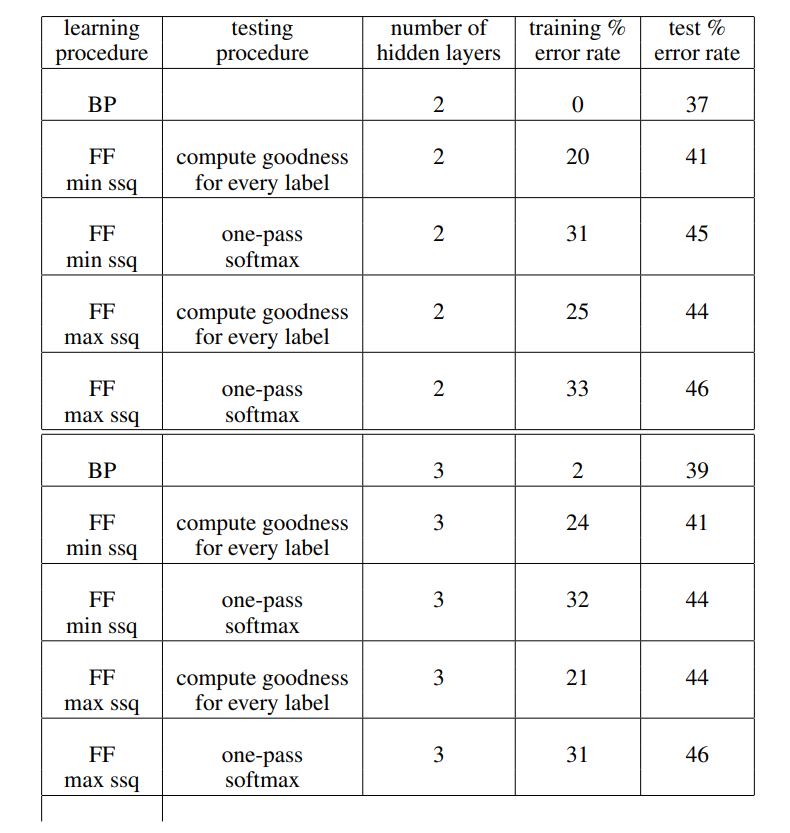
실험 결과입니다.

Compute goodness for every label : supervised task
One-pass softmax : unsupervised task

전반적으로 BackProp의 성능이 더 좋습니다.

특히 training error rate를 보면, overfitting에는 BP가 압도적인 성능을 보여주고 있습니다. 다만 test error rate를 보면 FF도 크게 밀리지 않는 성능을 내고 있습니다. FF의 가능성을 보여줬다, 정도로 이해하면 될 것 같네요.

Else

이 뒷부분은 뉴로모픽, 볼츠만 머신, GAN, Contrastive Learning 등과 FF의 관련성에 관한 추가 언급입니다. 관심 있는 분들은 직접 논문을 읽어보시길 추천합니다.

FF vs Backprop

Nebuly의 CTO Deigo Fiori가 FF와 Backprop을 비교한 포스트가 있습니다.

해당 포스트에 따르면, 네트워크의 레이어 수가 많아질수록 FF가 Backprop보다 메모리를 덜 사용합니다. 하지만 20개 이하의 레이어를 가진 thin network에서는 FF가 backprop보다 훨씬 더 많은 메모리를 사용합니다.

오차역전파 대체 알고리즘을 연구하는 가장 대표적인 이유가 큰 메모리 사용량인데, 그런 관점에서 볼 때는 아직 FF 알고리즘이 갈 길이 멀어보입니다. 하지만 BP와 달리 모듈별로 학습이 가능하다는 점과, 비동기적 학습에 대한 잠재적 발전 가능성까지 고려한다면 충분히 매력적인 알고리즘이라고 생각됩니다.

후속 연구가 기대되네요.

---

참고문헌

1. Keras Forward-Forward for Image Classfication example
2. mohammadpz's github implementation
3. Diego Fiori, FF vs Backprop