모든 Paper review는 제가 공부하고 남기는 기록입니다.
잘못된 내용이나 추가 의견이 있으시면 언제든 자유롭게 댓글 남겨주세요.

Published: IEEE, 2008
Paper: https://ieeexplore.ieee.org/abstract/document/4781121

---

[요약]

• Latent Factor Model에 preference $p_{ui},$ confidence $c_{ui}$ 개념을 도입

• implicit data의 핵심인 zero data를 다루는 새로운 관점 제시

---

[서론]

Abstract

implicit feedback에서 zero data가 내포하는 다양한 의미를 탐색하는 방법을 제시한 논문입니다. scalable optimization 방법과 explainable한 recommendation method (ALS)를 제안했습니다.

Introduction

사용자 데이터는 크게 Explicit Feedback과 Implicit Feedback 2가지로 나뉩니다.
전자는 호불호가 명확한 데이터(e.g. 별점)이고 후자는 호불호 없이 단순히 item을 얼마나 사용하였는지를 나타낸 데이터(e.g. 시청 횟수)입니다. Implicit Feedback을 활용하면 non-feedback item에 대한 잠재적 preference 정보를 추론할 수 있습니다.

논문에서는 implicit feedback의 주요한 특징 4가지를 언급합니다.

1. 부정적 피드백을 알 수 없다.

   negative feedback을 0으로 표시하기 때문입니다. Explicit Feedback에서는 호불호가 명확하므로, 해당 정보가 없는 0의 데이터는 무시하는 경향이 있습니다. 하지만 implicit feedback에서는 명확한 호불호 정보를 얻을 수 없으므로, 잠재적인 호불호 정보를 내포하는 이러한 0의 데이터를 분석에 포함해야 합니다.

2. Implicit feedback은 태생적으로 노이즈가 많다.

   동일한 데이터를 여러 관점에서 해석할 수 있다는 뜻입니다. TV를 하루종일 틀어놨다고 해서 꼭 전부 보고 있었다는 보장은 없는 것과 같습니다. TV를 켜 놓고 다른 일을 하거나 잤을 수도 있겠죠.

3. Explicit feedback은 preference를, implicit feedback은 confidence를 의미한다.

   여기서 말하는 confidence는 (추론의) 신뢰도를 가리킵니다. 예를 들어, 어느 영화를 여러 번 봤다면 user는 해당 영화를 좋아할 가능성이 높다는 뜻입니다. 물론 이것도 데이터의 특성에 따라 다릅니다. 예컨대 드라마는 여러 회차로 구성되므로, 영화보다 value가 평균적으로 높습니다.

4. Implicit feedback 기반 추천은 적합한 평가 기준이 필요하다.

   앞서 언급한 것처럼, 데이터의 특성 차이로 인해 value가 의미하는 것이 다를 수 있으므로 적합한 평가 지표가 필요합니다.

[본론]

전제

유저 $u$, 아이템 $i$에 대해 user와 item의 associate value를 $r_{ui}$ (observation) 이라고 합니다.

Neighborhood models

비슷한 item이나 비슷한 user 정보를 기반으로 분석하는 방법입니다. 따라서 유사도 기반의 방법을 사용합니다.

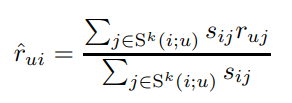
user based보다 item based가 accuracy, scalability 측면에서 더 좋은 경우가 많습니다. 사람들은 자신과 비슷한 사람은 잘 모르지만, 선호하는 아이템과 비슷한 것은 쉽게 좋아하기 때문입니다.

Latent factor models

SVD 기반의 방법론입니다. user latent vector $x_u \in \mathbb{R}^f$, item latent vector $y_i \in \mathbb{R}^f$를 각각 축으로 삼습니다. 일반적으로 다음과 같은 Loss function을 사용합니다. $\lambda$는 regularization parameter입니다.

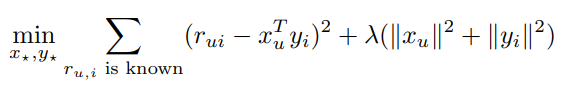
Paper's Model

논문에서는 사용자의 preference 정보를 나타내기 위해 binary variable $p_{ui}$를 사용합니다.

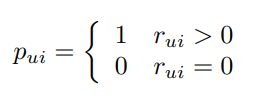
preference에 대한 confidence 정보를 나타내는 변수 $c_{ui}$도 제안했습니다. $\alpha$는 $r_{ui}$값을 조절하는 파라미터입니다. $\alpha=40$일 때 가장 좋은 결과를 냈다고 합니다.

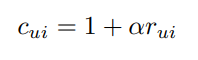
user factor $x_u \in \mathbb{R}^f$, item factor $y_i \in \mathbb{R}^f$일 때, preference 값은 두 벡터의 내적이 됩니다.

여기서 언급하는 $p_{ui}$값은 binary variable $p_{ui}$와 다릅니다. 전자는 모델의 prediction이고 후자는 데이터에 따른 one hot encoding 값입니다.

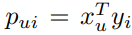
결과적으로 다음과 같은 cost function을 사용하게 됩니다. m=num of users, n=num of items 입니다. $\lambda$값은 cross validation으로 결정합니다.

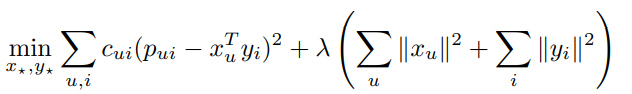
ALS (Alternate Least Square)

모델은 user factor $x_u$와 item factor $y_i$ 두 개를 학습해야 합니다. 그리고 두 factor matrix는 $x_u^Ty_i$ 형태로 묶여 있습니다.

문제는, 학습을 위해 사용되는 대부분의 최적화 알고리즘(대표적으로 SGD)에 대해 두 변수를 동시에 최적화하는 것은 NP problem (확률에 따라 비효율적일 수 있는) 경우에 속한다는 것입니다. 특히 implicit feedback data처럼 데이터 규모가 큰 경우에는 더더욱 그렇습니다.

이에 따라 논문에서는 Alternate Least Square 라는 방법을 제안합니다. ALS의 아이디어는 다음과 같습니다.

"한 번에 두 개를 최적화하기 힘들면, 하나씩 처리하면 되지!"

1) Computing user/item factors

먼저 item factor를 상수로 놓고 user factor에 대해 편미분합니다.

동일한 방법으로 다음과 같이 $y_i$도 구할 수 있습니다.

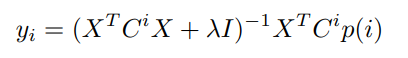
이상의 과정을 번갈아가며 두 변수를 최적화합니다. 10~15회 정도가 적당하다고 하지만, 데이터 크기에 따라 유동적인 부분입니다.

2) Time Complexity

앞서 대량의 데이터를 처리하기 위한 시간복잡도가 문제라고 했었죠. $(n\times f)$ 크기의 item factor matrix에 대해 ALS의 시간 복잡도는 다음과 같습니다.

연산 병목은 $Y^TC_uY$에서 발생합니다. 이 연산은 $O(f^2n)$의 시간복잡도를 갖습니다.

이 때 $Y^TC_uY=Y^TY+Y^T(C_u-I)Y$ 으로 치환할 수 있습니다. $Y^TY$는 유저 수에 상관없이 시간복잡도가 일정합니다.

$(C_u-I)Y$의 경우, $(C_u-I)$는 $n_u$개만큼의 non-zero 값을 갖습니다. 바꿔 말해 $n_u$는 $r_{ui} > 0$인 아이템 수입니다. 당연히 $n_u \ll n$ 이겠지요.

마찬가지로 $C_up(u)$는 $n_u$개의 non-zero 원소를 가집니다. $(Y^TC_uY+\lambda I)^{-1}$의 경우 $O(f^3)$의 시간복잡도를 갖습니다.

결과적으로 user factor $x_u$는 $O(f^2n_u+f^3)$ 안에 계산할 수 있습니다.

이상의 연산은 m명의 유저마다 진행되므로, $\sum_u n_u = N$에 대해 시간복잡도는 $O(f^2N+f^3m)$가 됩니다. 따라서 ALS 알고리즘의 시간복잡도는 input size에 따라 선형적으로 변하는 것을 알 수 있습니다. (논문에서는 일반적으로 $20 \le f \le 200$의 값을 갖는다고 합니다.)

3) Explainable Recommendation

ALS의 강점은 선형적 시간복잡도 외에도 설명가능한 추천을 제시한다는 것입니다.

user factor $x_u=(Y^TC_uY+\lambda I)^{-1}Y^TC_up(u)$ 이고, user $u$와 item $i$의 preference 값 $\hat p_{ui}=x_u^Ty_i=y_i^Tx_u$ 이므로, $\hat p_{ui}=y_i^T(Y^TC_uY+\lambda I)^{-1}Y^TC_up(u)$가 됩니다.

이 때, $(f\times f)$ 크기인 행렬 $(Y^TC_uY+\lambda I)^{-1}=W^u$로 놓으면, $\hat p_{ui}=y_i^TW^uY^TC_up(u)$가 됩니다.

$C_u$는 confidence 값들을 모아 놓은 대각행렬이고, $Y$는 아이템 정보 행렬, $p(u)$는 사용자의 preference값을 모아 놓은 벡터입니다. 따라서 $W^u$를 user $u$의 선호도에 대한 가중치로 보는 것이 합리적인 해석이 됩니다.

그렇다면 user $u$가 보는 item $i, j$에 대한 유사도 예측값은 다음과 같이 표현할 수 있습니다.

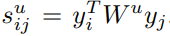
결과적으로 $\hat p_{ui}$는 다음과 같이 정리할 수 있습니다.

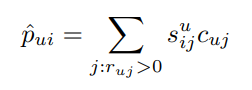
$C_{uj}$는 $u$의 $j$에 대한 선호도입니다. 원래 식에서 $C_up(u)$와 같은 역할입니다. $s_{ij}^u$는 $u$가 $i, j$ 두 아이템을 얼마나 비슷하게 보냐에 관한 정보를 담고 있습니다. 따라서 두 값을 곱해주면 $u$가 $j$를 얼마나 좋아하는지를 가지고 $u$의 $i$에 대한 preference를 예측할 수 있습니다.

여기서 중요한 부분은 $C_{uj}$와 $s_{ij}^u$를 따로 분리해냈다는 점입니다. neighborhood based에 비해 유저별로 세밀한 선호도 정보를 얻을 수 있다는 것이죠.

Experiments

1) Data Description

각각의 user $u$와 item $i$에 대해 $r_{ui}$값은 $u$가 얼마나 $i$를 보았는가를 나타냅니다. 논문에서 사용한 데이터에는 약 320만 개의 non-zero $r_{ui}$값이 포함돼 있습니다.

전체 $r_{ui}$ 개수는 300,000 * 17,000 = 5,100,000,000 개 이므로 실험에 사용한 implicit feedback data가 상당히 sparse함을 알 수 있습니다.

더 정확한 실험을 위해 $r_{ui}^t < 0.5$인 $r_{ui}^t$를 전부 0으로 변환했습니다. 잔여 non zero value는 약 200만개까지 감소했습니다.

confidence computing method를 조금 변형하여 $C_{ui}=1+\alpha \log(1+{r_{ui} \over \epsilon})$ 식을 사용했습니다. $\epsilon$ 값은 $10^{-8}$로 설정했습니다.

TV 시청자의 행동 특성을 고려하여 한 채널에서 여러 프로그램을 보는 경우, ${e^{-(at-b)} \over 1+e^{-(at-b)}}$ 꼴의 가중치를 통해 noise를 감소시켰습니다. (논문에서는 $a=2, b=6$으로 설정했습니다.)

2) Evaluation methodology

평가는 다음과 같은 과정으로 이루어졌습니다.

1. user별 recommended item list를 선호도에 따른 내림차순으로 정렬
2. negative feedback이 없으므로 precision이 아닌 recall 기반 지표 사용

논문에서 사용한 recall 기반 지표는 다음과 같습니다.

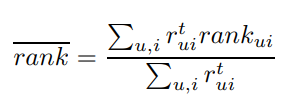
$rank_{ui}$는 전체 프로그램 중에서 $u$에게 추천한 $i$의 백분율 값입니다.

실험 중에는 피드백을 받을 수 없기 때문에, 정렬한 리스트에서 해당 아이템이 몇 번째인지를 통해 얼마나 잘 추천하고 있는지를 살펴볼 수 있습니다. 따라서 $\overline{rank}$ 값이 낮을 수록 좋은 추천이라고 할 수 있습니다. (baseline은 50%)

3) Evaluation Results

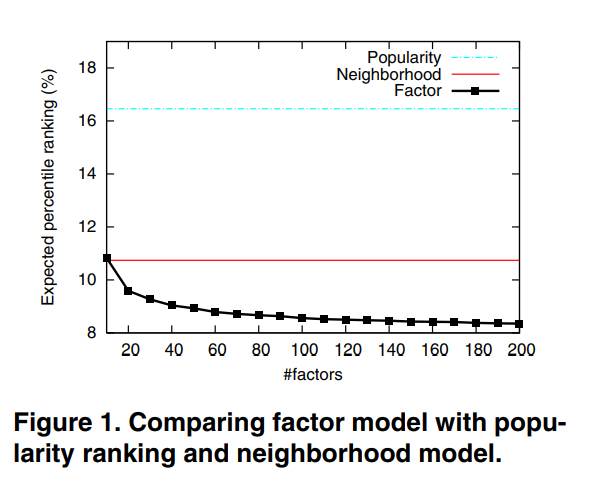
Fig. 1.을 보면 논문에서 제시한 모델이 가장 성능이 좋습니다. 또, factor 수에 따라 성능이 추가적으로 향상되었습니다. 그 외에 기존의 Latent factor model과 $p_{ui}$만 사용한 모델도 실험했는데, full model이 더 성능이 좋았습니다.

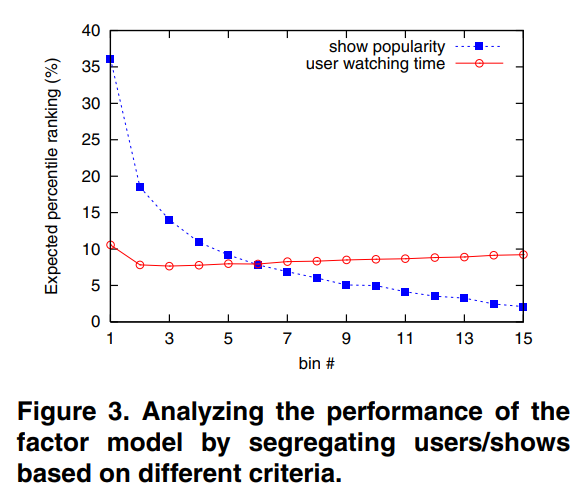
특이한 점은 user watching time과 show popularity 두 가지 기준에 따라 데이터 그룹을 15개로 분할했을 때, 추천의 성능이 변화하는 양상이 달랐다는 것입니다. (1번이 가장 인기가 많고/시청 시간이 긴 그룹)

Fig. 3.을 보면 explicit feedback 데이터와 달리 데이터 양에 따라 성능 차이가 크지 않음을 알 수 있습니다. watching time에 따른 성능 변화는 거의 없는 반면에 popularity에 따른 성능 변화는 상당합니다.

논문에서는 원인에 대해 많은 사람들이 비슷한 프로그램을 봤기 때문이라고 추정했습니다.

---

참고문헌

1. P, NP 문제
2. 갈아먹는 추천 알고리즘[4] Alternating Least Squares
3. Matrix Completion via Alternating Least Square(ALS)