[추천시스템] LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
Papers Review

모든 Paper review는 제가 공부하고 남기는 기록입니다.
잘못된 내용이나 추가 의견이 있으시면 언제든 자유롭게 댓글 남겨주세요.Published: SIGIR, 2020
Paper: https://arxiv.org/abs/2002.02126
요약
-
기존 방법(NGCF, GCN)에서 불필요한 모듈을 제거
-
User-item interaction data의 단순성을 지적하고, 이에 맞게 경량화시킨 LightGCN을 제안
What's new & work importance
Ablation study를 통해 기존 모델에서 불필요한 부분을 찾아내고, 이를 개선한 LightGCN을 제시한 논문입니다. 모델이 무겁지 않고 구현이 쉬워서 추천시스템 분야에서 baseline으로 널리 사용되고 있습니다.
Background
User-item interaction data를 통해 유저 행동과 아이템 평점에 영향을 주는 요인을 찾을 수 있다.
Collaborative Filtering에는 위와 같은 대전제가 존재합니다. 여기서 '유저 행동과 아이템 평점에 영향을 주는 요인'을 Latent Factor라고 하는데, 이를 효율적으로 찾기 위해 제안된 모델 중 하나가 Neural Graph Collaborative Filtering (NGCF)입니다. NGCF는 그래프 구조를 활용해서 기존의 DNN 기반 추천 모델보다 더 나은 표현 능력을 가질 수 있게 한 모델이라고 할 수 있는데요. Base architecture를 GCN에서 따오는 과정에서 본래 목적 달성에는 필요 없는 모듈까지 포함하게 되었다는 것이 본 논문의 핵심 이슈입니다. 'LightNGCF'가 아니라 'LightGCN'인 것도 이런 이유라고 할 수 있죠.
What's the problem?
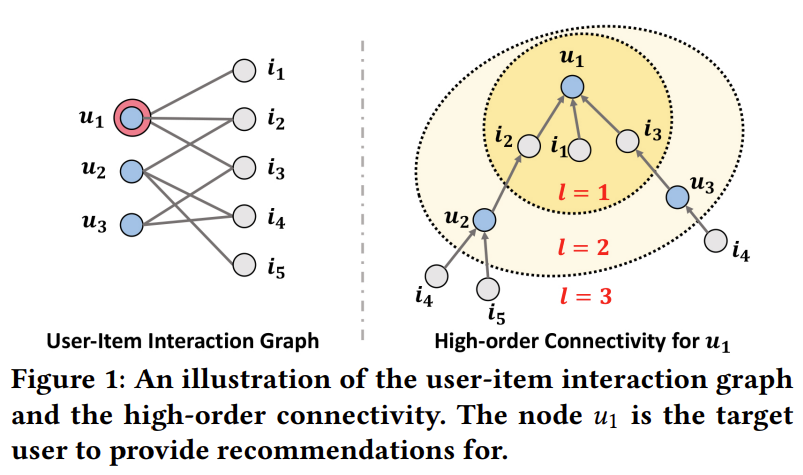
그래프 구조의 특징 중 하나는 순서를 부여할 수 있다는 것입니다. 예를 들어, NGCF에서는 오른쪽 그림과 같이 High-order Connectivity라는 개념을 도입해서 hierarical representation을 생성합니다.
물론 interaction matrix를 곧바로 이렇게 매핑하는 것은 매우 복잡하고 어렵습니다. 그래서 여타 DNN 모델처럼 propagation을 사용해서 임베딩을 업데이트하는 방식을 채택했는데, propagation을 위한 행렬곱 연산 중에 몇 가지 문제가 발생하는 단점이 있었습니다.
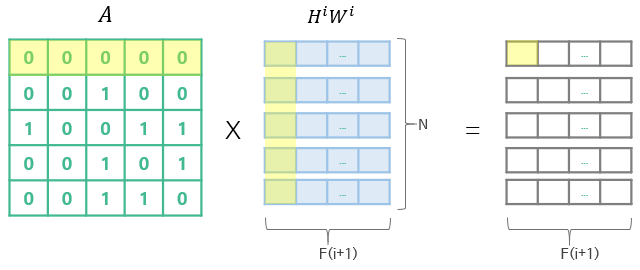
예를 들어 위와 같이 연산이 진행되면 노드는 자기 자신의 정보를 반영할 수 없습니다. 따라서 자신의 정보를 반영하기 위해 별도의 self-loop이 필요합니다.
또, edge가 많이 연결된 그래프는 embedding matrix에서 값이 커지기 때문에 기울기 폭발/소실이 발생할 수 있습니다. 그래서 별도의 정규화 연산이 필요합니다.
실제로 NGCF의 embedding rule을 보면 다음과 같습니다.
위 수식을 보면 self connection을 통해 자기 자신의 정보를 반영하고, 각 레이어의 연산 결과에 symmetric normalization 을 적용하여 정규화를 해주고 있습니다.
결과적으로 NGCF는 user-item interaction matrix를 투입했을 때 개의 레이어를 통과하여 개의 임베딩 를 얻을 수 있으며, 각각의 임베딩 벡터들을 concat하여 최종 user-item embedding으로 사용하는 구조가 되는데요.
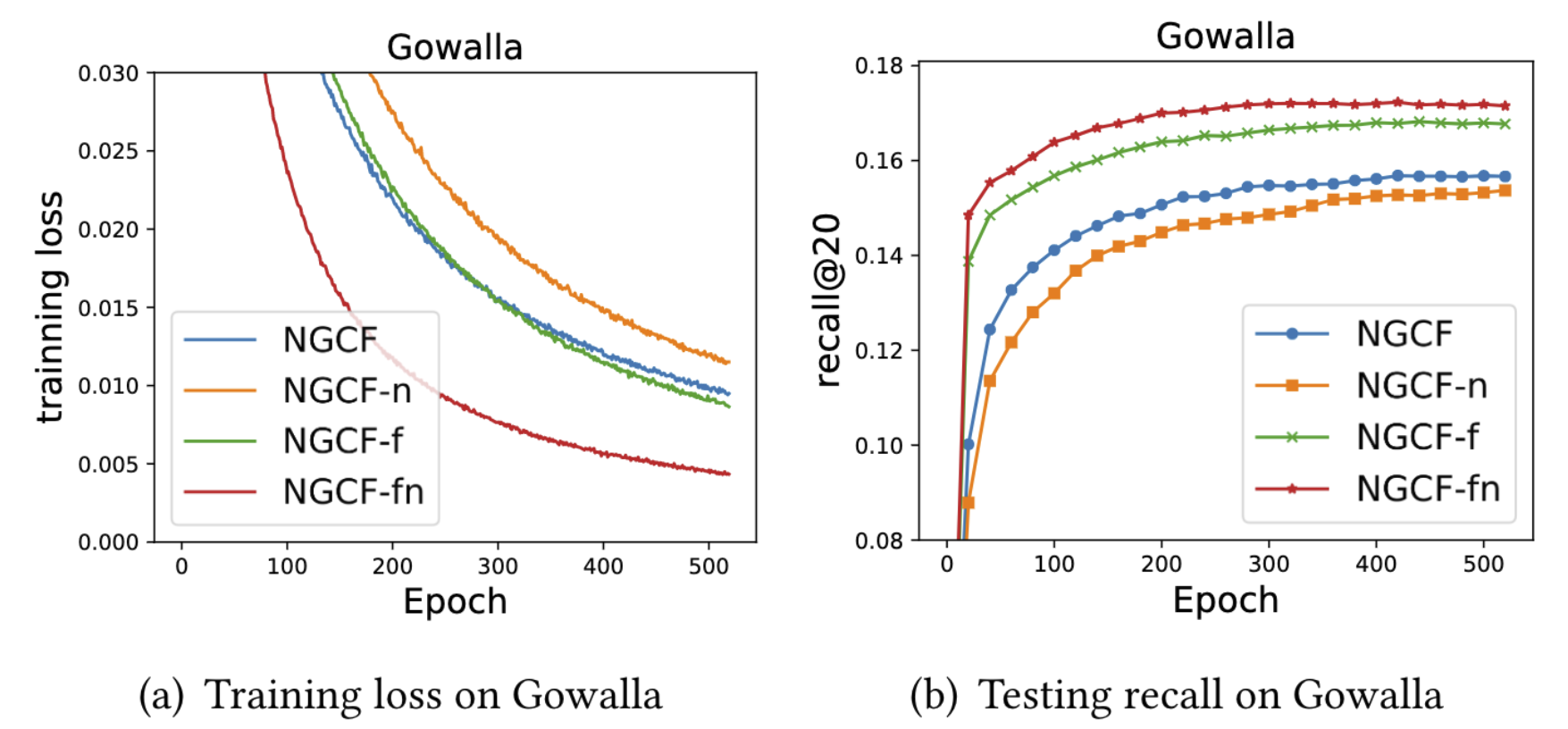
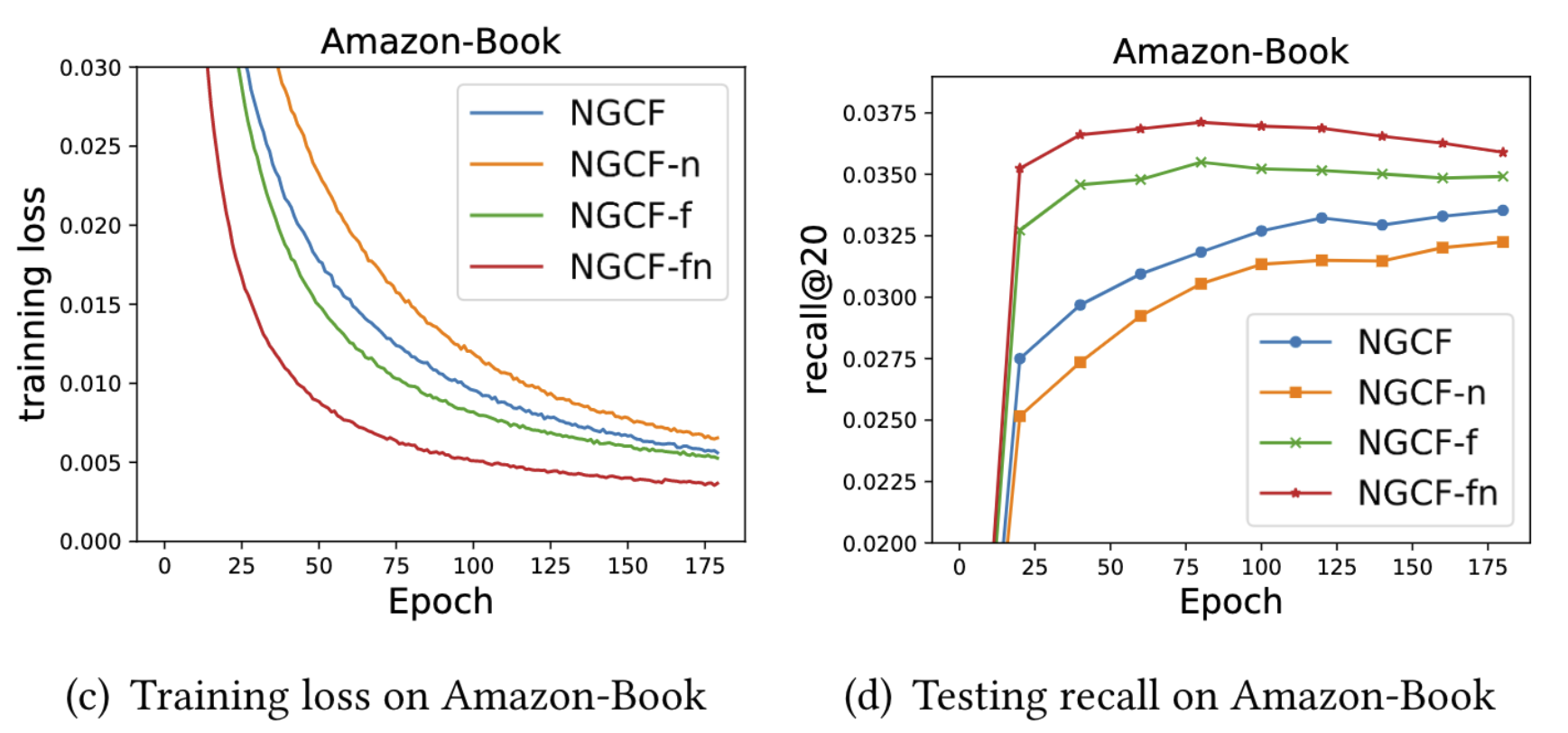
NGCF-n : 가 없는 버전
NGCF-f : feature transformation이 없는 버전
NGCF-fn : 둘 다 없는 버전
논문의 실험 결과에 따르면 feature transformation에 해당하는 와 nonlinear activation function 가 성능에 오히려 악영향을 끼치고 있습니다. 반대로 대부분의 성능 향상에 기여하는 것은 neighborhood aggregation에 해당하는 연산입니다.
저자들에 따르면 본래 GCN은 raw input feature처럼 rich한 features를 가진 attributed graph 위의 노드들을 구분하기 위한 것이므로, user-interaction matrix처럼 개별 노드가 non-semantic한 경우에는 적합하지 않다고 합니다.
쉽게 말해서 user-item interaction matrix를 그래프 임베딩으로 바꾸었을 때, 각각의 노드가 어떤 의미를 갖는 것이 아니라 단순히 상호 관계를 나타낼 뿐이라는 것입니다. 따라서 각각의 임베딩 간에 어떠한 우열 관계가 없으므로 feature transformation이 필요 없고, nonlinear한 semantic information이 존재하지도 않으므로 non-linearity를 표현하기 위한 function를 사용할 필요도 없어지게 됩니다. 한 줄로 요약하면 단순한 데이터에 굳이 복잡한 모듈을 사용할 필요가 없다라고 할 수 있겠네요.
물론 이는 어디까지나 현재 통용되는 one-hot encoding 형태의 interaction matrix일 때 그렇다는 것이기 때문에 semantic information을 다량 포함하는 형태의 input data(e.g. 리뷰 등의 자연어 데이터)를 사용할 때는 다른 방식을 찾아야 할 겁니다.
Model Architecture
Light Graph Convolution
자, 문제를 알았으니 이제 해결을 해야겠죠?
논문에서는 Light Graph Convolution (LGC)이라는 해결 방안을 제안합니다. 크게 변형을 준 건 아니고, 앞서 언급한 nonlinear activation과 feature transformation을 제거하고 neighborhood aggregation만 남겨놓은 것입니다.
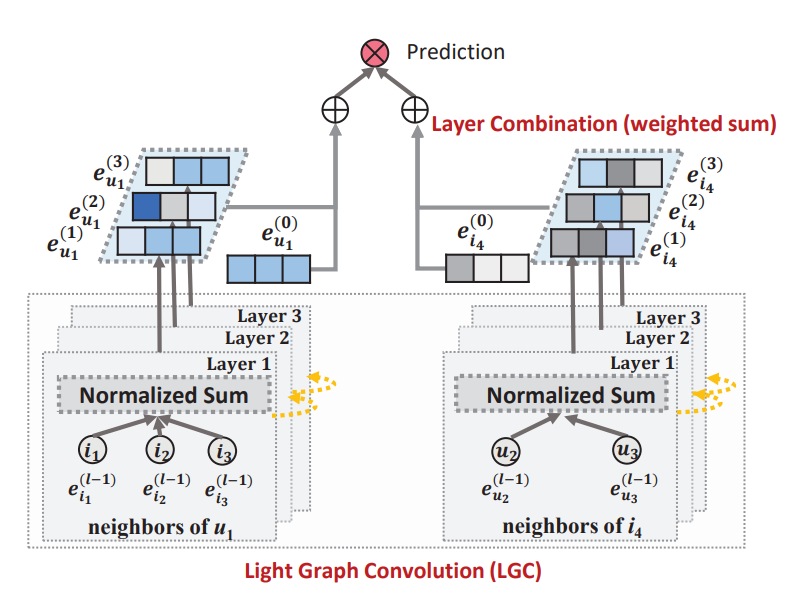
그림만 봐도 알 수 있지만 간단하게 설명하자면, 먼저 레이어마다 각각의 임베딩에 대해 normalized sum을 수행합니다. 이렇게 얻은 임베딩 벡터 들을 모아 weighted sum하면 최종 임베딩을 얻을 수 있습니다. 수식으로 나타내면 다음과 같습니다.
graph convolution 과정에서 임베딩 값이 지나치게 커지는 것을 방지하기 위해 symmetric normalization term은 그대로 유지합니다. 실험 결과 다른 regularization 대신 이 방식을 사용하는 게 가장 성능이 좋았다고 하네요. 비교 결과는 논문의 table 5에서 확인할 수 있습니다.
Layer Combination and Model Prediction
그런데 LightGCN에는 특이한 점이 하나 있습니다. 바로 첫 번째 레이어의 임베딩 파라미터 만 학습이 가능하다는 것입니다. 직관적으로 생각해 봤을 때, 그래프 구조 상 첫 번째 임베딩 파라미터가 성능을 결정하는 데 가장 큰 역할을 할 것이므로 첫 번째 레이어만 학습을 시킨다면 오히려 효율적인 학습이 가능해진다고 할 수 있겠죠?
이후 개의 레이어를 거치면서 얻는 representation들을 간단한 weighted sum으로 합쳐 줍니다. 수식으로 나타내면 다음과 같습니다.
는 최종 임베딩에 대한 번째 레이어의 기여도를 나타냅니다. 값도 학습이 가능하지만 논문에서는 모델의 단순성을 유지하기 위해 별도의 학습 모듈을 추가하지 않았습니다. 자체적으로 실험을 돌려봤을 때는 로 세팅하는 것이 좋다고 합니다.
일반적으로 sequential하게 레이어들을 거치게 되면 뒤쪽 레이어로 갈 수록 정보가 제한됩니다. 물론 전달되는 정보의 질이 향상될 것이라는 기대를 하지만, 정말로 그런지는 알 수 없기 때문에 각 레이어의 영향력을 uniform하게 세팅하는 것이 좋은지에 대한 의문이 생길 수 있습니다.
이에 대해 간단한 추론을 해 보자면, 먼저 user-item interaction matrix의 기저에는 user/item 수만큼의 preference 분포가 존재할 것입니다. 이들은 모두 한 줄의 user vector로 표현되며, 각각의 user vector 간에 우열 관계가 없으므로 모든 preference 정보는 균등하게 분포한다고 할 수 있습니다. 물론 개중에 상대적으로 active한 user가 있겠지만 이는 개별 preference에 대한 정보의 밀도에 관여할 뿐 각 preference 분포의 중요도에는 영향을 미치지 않을 것입니다. User-item matrix처럼 극도로 sparse하면서도 interaction의 숫자가 수십만이 넘어가면 개별 user의 preference 분포의 density의 영향력이 작아지기 때문입니다.
그리고 이렇게 되면 각각의 preference information을 내포한 그래프 임베딩에는 정보가 전반적으로 고르게 분포할 것이란 예측도 가능합니다. 따라서 hop으로 정보를 추출할 때 값에 상관없이, 다시말해 몇 번째 레이어인지에 상관 없이 고루 정보를 추출할 것이라는 결론에 도달할 수 있습니다.
또한 논문에서는 왜 한번에 embedding을 뽑지 않고 layer combination한 결과를 사용하는지에 대해 아래와 같이 설명합니다.
- 레이어 수가 늘어나면 임베딩들이 over-smooth 됩니다.
GCN에서 smoothing이란 주변 노드들의 정보를 취합하는 것을 말합니다. Over-smoothing은 GCN의 고질적인 문제 중 하나인데, 네트워크가 깊을 수록 여러 레이어를 거치면서 local information 정보를 잃어버리고 global information만 보게 되는 현상을 가리킵니다.
위와 같이 그래프 전반을 보게 되어 결과적으로 임베딩이 다 비슷해지게 되는 문제가 발생합니다.
그 외에도 다음과 같은 장점들이 있습니다.
- 각각의 레이어는 서로 다른 semantic을 내포합니다.
- 각각의 레이어에서 출력한 임베딩을 가중합하여 self-connection 효과를 얻을 수 있습니다.
마지막으로 모델의 최종 예측 결과는 다음과 같이 각 final embedding을 서로 내적하여 얻을 수 있습니다.
Matrix Form
이상의 과정을 matrix form으로 한 번 살펴보겠습니다.
명의 user와 개의 item에 대해 user-item interaction matrix 이라고 가정합니다. 이 때 의 원소 의 값은 0 or 1입니다. 그러면 user-item graph를 나타낸 adjacency matrix A는 다음과 같습니다.
0th layer의 임베딩을 (는 임베딩 크기)라 하면, 앞에서 살펴본 LGC 식을 다음과 같이 바꿀 수 있습니다.
는 크기의 diagonal matrix입니다. 이 때 의 원소 는 adjacency matrix 의 번째 행벡터에 존재하는 nonzero entry의 개수를 나타냅니다. 그러면 최종적으로 prediction에 사용하는 embedding matrix는 다음과 같이 구할 수 있습니다.
이 때 는 symmetrically normalized matrix입니다. 를 알고 있다면 만 거듭해서 곱해주면 앞서 각각의 최종 임베딩을 구할 수 있으므로, 앞서 언급한 것과 같이 효율적인 계산이 가능합니다.
Self-connection in SGCN (Simplified GCN)
또한 LightGCN은 별도의 self connection 모듈이 필요하지 않습니다.
위와 같이 식 (1)에 self connection 모듈이 추가되어 identity matrix 를 더해준다고 가정해보겠습니다. 식 (3)에서 편의상 를 생략하고 추론에 사용되는 마지막 레이어의 임베딩을 수식으로 표현하면 다음과 같습니다.
이항정리를 이용해 식 (3)을 계산해보면 식 (2)와 같다는 걸 알 수 있습니다. 따라서 LGC는 self-connection을 이미 포함하고 있다고 할 수 있습니다.
Alleviate Oversmoothing
GCN과 Personalized PageRank를 연결한 APPNP라는 모델이 있습니다. APPNP는 넓은 범위의 large neighborhood information을 고려할 때, initial embedding을 더해줌으로써 root node의 정보를 잃지 않도록 설계되었는데, 그 덕분에 oversmoothing에 강하다는 특징이 있습니다.
APPNP의 propagation layer는 다음과 같이 표현할 수 있습니다.
여기서 는 의 반영 비율을 나타내는 확률변수입니다. 따라서 은 까지의 임베딩과 의 가중합이 됩니다. 식 (3)과 비슷하죠?
Second-order Embedding Smoothness
LightGCN이 선형적이고 단순하기 때문에 임베딩을 smoothing 하는 과정을 분석해보면 더 많은 인사이트를 얻을 수 있습니다. 예를 들어 2개의 레이어를 가진 LightGCN을 수식으로 나타내면 다음과 같습니다.
만약 user 가 target user 와 같은 item에 상호 작용한 기록이 있다면, 두 유저간 smoothness의 강도는 다음과 같은 coefficient로 나타낼 수 있습니다.
식 (4)를 잘 살펴보면 두 유저의 interaction history 간에 겹치는 아이템의 수가 많으면 계수가 증가합니다. 만약 겹치는 아이템이 인기가 많은 상품이라면 계수가 감소합니다. 의 action history가 적으면 계수가 증가합니다. 상당히 직관적이죠. 유저 간의 유사도를 살펴본다는 collaborative filtering의 basic assumption에도 부합합니다.
Model Training
LightGCN에서 학습 가능한 파라미터는 오직 initial embedding 뿐입니다. 따라서 Standard Matrix Factorization과 computation complexity가 동일합니다.
논문에서는 손실함수로 Bayesian Personalized Ranking (BPR)을 사용했습니다. BPR은 선호하는 아이템에 대한 예측값이 나머지보다 높도록 유도하는 pair-wise optimization 기법입니다.
식 (5)에서 는 가 선호하지 않는 item이라고 할 수 있습니다. (싫어하는 아이템이 아닙니다.) 따라서 는 가 선호하는 아이템만 평가의 대상으로 남기는 역할을 하게 됩니다. Bayesian적인 접근이라고 할 수 있죠.
이후 를 통해 regularization을 해줍니다. L2 norm 으로도 충분하기 때문에 따로 dropout까지는 필요 없습니다.
Experiments
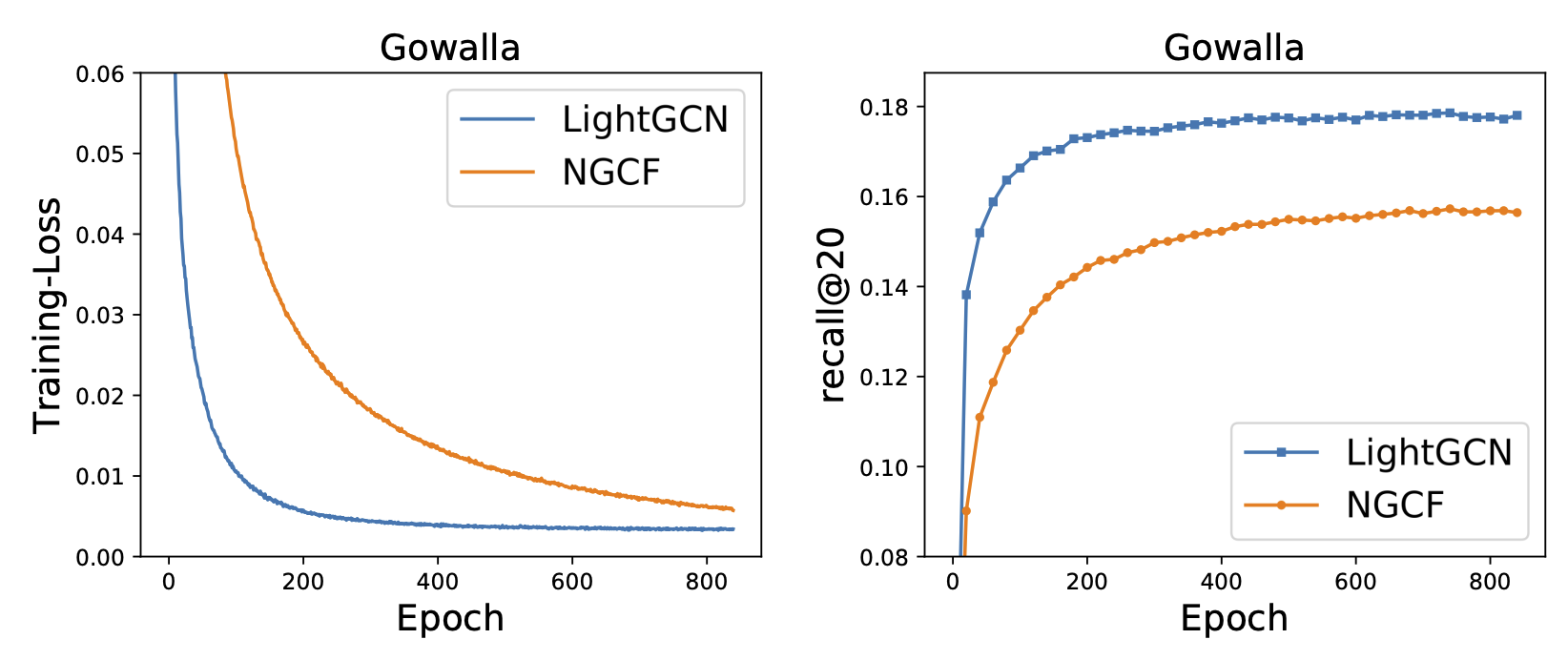
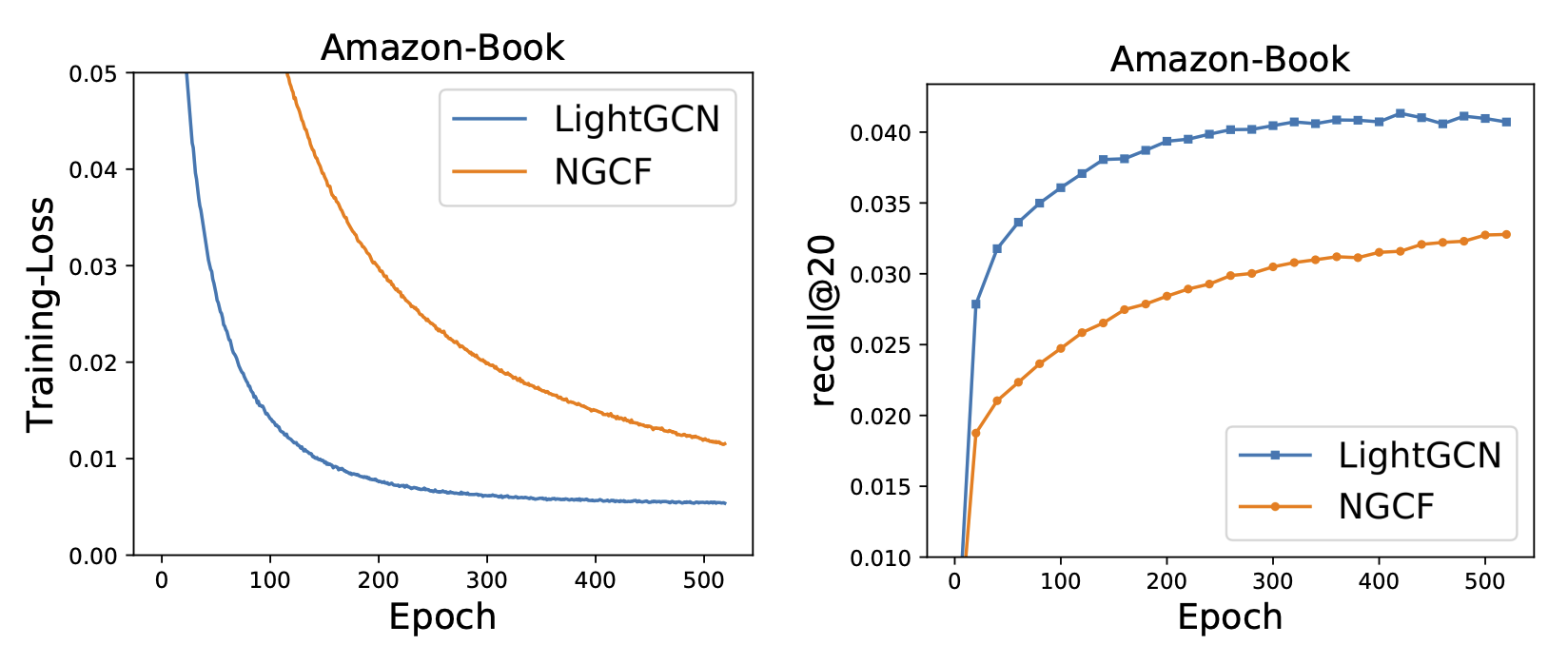
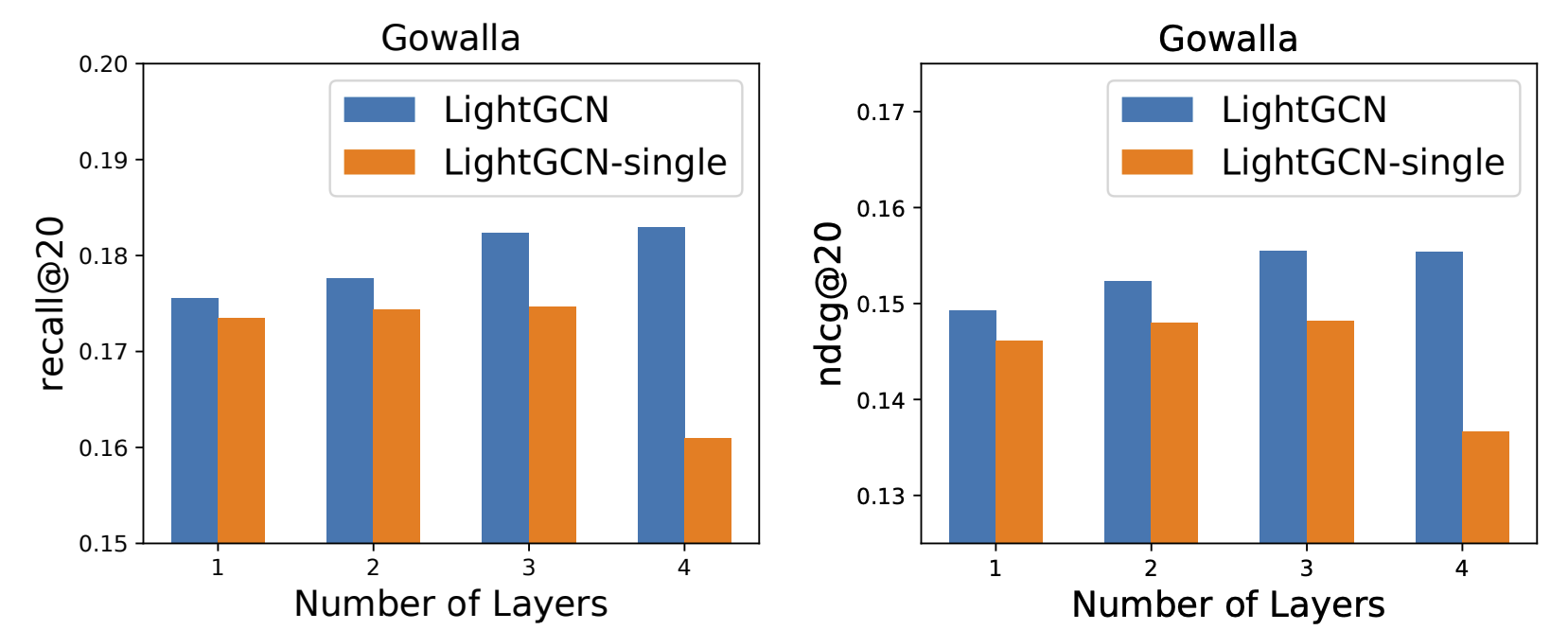
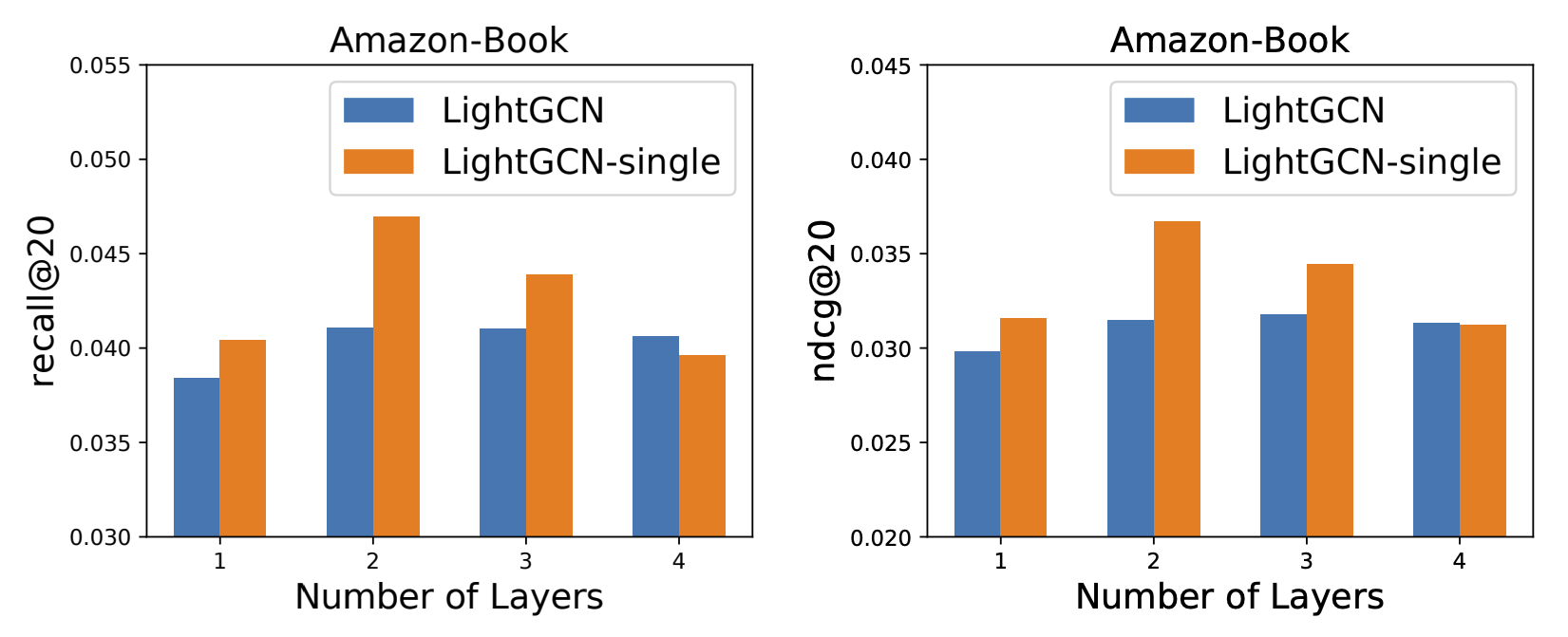
실험 결과, LightGCN이 수렴 속도도 빠르고 성능도 더 좋았다고 합니다. 자세한 실험 내용이 궁금하면 논문을 참고하세요.
참고문헌

