[NLP] Attention Is All You Need (Transformer)

Ethan·2023년 8월 12일

NLP transformer

Papers Review

목록 보기

13/19

Published in NIPS 2017

요약

Attention 모듈만으로 만들어진 transformer 모델을 제안
- 압도적인 성능과 확장성을 보유
구현체가 무겁고 막대한 데이터와 컴퓨팅 자원을 요구하는 단점 존재
- 계산 복잡도가 $O(n^2)$

What's new & work importance

Transformer는 제목처럼 attention 모듈만 사용해서 만들어진 모델입니다. 트랜스포머 기반 모델의 핵심적인 특징 중 하나는 inductive bias가 아예 없다시피하다는 점인데 이로 인해 학습에 많은 데이터가 필요합니다. 또한 성능적인 측면에서도 데이터를 계속해서 집어넣으면 지속적으로 성능이 향상되는데, 이론적으로 이러한 모델은 많지만 실전에서도 이러한 능력이 발휘되는 모델은 많지 않습니다. 실제로 트랜스포머 기반 구현체에 데이터를 계속 축적해온 결과가 BERT, GPT 같은 LLM들입니다.

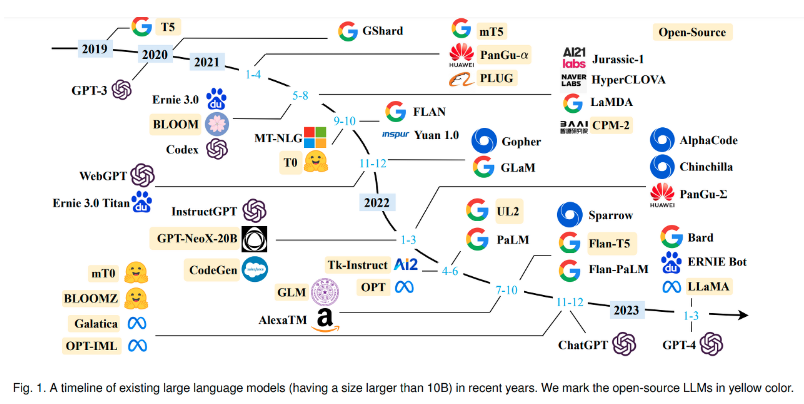
LLM에서 나타나는 또다른 특징은 바로 Emergent Ability 라고 부르는 성능적 특이점입니다. 일정 수준 이상의 파라미터를 가진 모델이 충분한 데이터를 학습하면 해당 포인트 이전까지는 없던 독특한 성능(ability)이 생겨나는(emergence) 현상을 말합니다.

물론 이러한 현상이 반드시 transformer 구조로 인해 생겨난다는 것은 아니지만 현재(23년 8월) 기준으로 transformer 외에 이러한 독특한 변화가 나타나거나 널리 사용되는 base architecture는 사실상 없습니다.

Background

Transformer가 처음 나왔을 당시에는 RNN, LSTM 등의 recurrent model들이 대세를 이루고 있었습니다. 이러한 모델들은 정해진 길이의 context vector를 사용하기 때문에 그 이상의 정보는 삭제돼 버리는 bottleneck problem과 long term dependency 문제가 있었습니다. CNN을 block처럼 사용해서 hidden representation을 병렬로 계산하려는 시도들[1][2][3]도 있었습니다만 transformer가 등장하고 나서는 다들 transformer 기반의 메타로 넘어갔습니다. 물론 MLP-mixer 등의 논문을 통해 다양한 base architecture에 대한 연구들도 여전히 진행되고 있습니다.

Model architecture

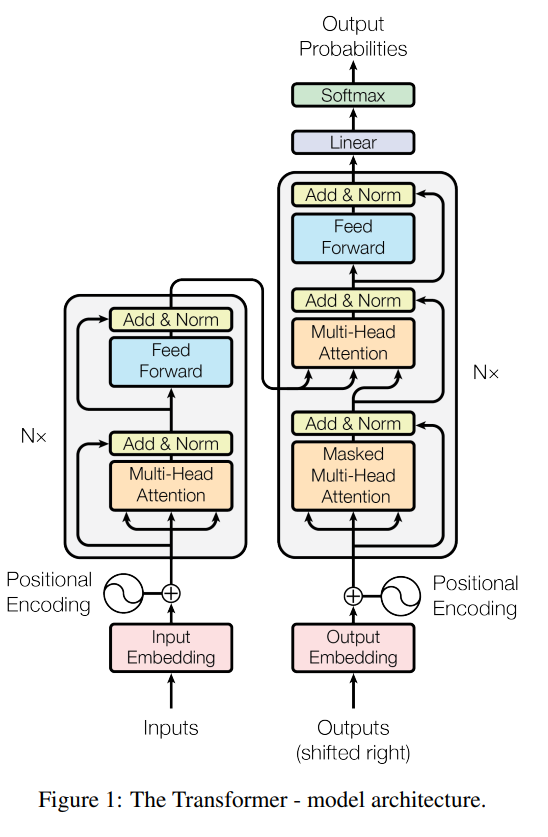
트랜스포머의 전체 모델 구조입니다.

Encoder & Decoder

트랜스포머는 기본적으로 인코더-디코더 구조를 가지고 있습니다.

인코더와 디코더는 각각 동일한 레이어를 6개씩 쌓은 구조입니다. 인코더의 레이어는 sublayer 2개, 디코더의 레이어는 sublayer 3개로 구성돼 있습니다. 인코더와 디코더에서 사용하는 모든 모듈은 사전에 지정한 $d_{model}=512$ 의 차원을 갖습니다.

먼저 인코더의 sublayer를 살펴보면, 하나는 multi head self-attention이고 다른 하나는 fully connected layer입니다. 각 sublayer의 출력은 residual connection으로 넘겨받은 원본 데이터와 함께 layernorm을 거쳐 다음 레이어로 전달됩니다. 즉, 각 sublayer의 출력 $y$ 는 다음과 같이 나타낼 수 있습니다.

y=\text{LayerNorm}(x+\text{Sublayer}(x))

디코더의 sublayer는 인코더에서 multi head attention 모듈이 하나 새롭게 추가되었고, 데이터에 masking 하는 기능도 포함하고 있습니다. Sequence data를 다루기 때문에 뒤쪽 정보를 미리 아는 것은 일종의 치팅이므로, masking으로 이를 방지합니다. 이론상으로는 $-\infty$ 를 사용하여 마스킹을 해야 하지만 실제 구현에서는 $-1e9$ 등의 아주 큰 음수 값을 대신 사용합니다.

Positional Encoding

트랜스포머는 attention 외의 다른 모듈이 없습니다. 그런데 attention은 기본적으로 단순한 내적 기반 연산이기 때문에 CNN이나 RNN처럼 input data의 time step 정보를 잡아내는 능력이 없습니다. 그래서 positional information을 넣어주는 과정이 필요합니다.

여러 가지 방법이 있지만 오리지널 트랜스포머에서는 (코)사인 함수를 사용하여 positional information을 인코딩합니다.

PE(pos, 2i)=sin(pos/10000^{2i/d_{model}})\\ \quad\\ PE(pos, 2i+1)=cos(pos/10000^{2i/d_{model}})

위 식에서 $i$ 는 차원의 인덱스이고 $pos$ 는 주어진 sequence 내에서 임베딩 벡터의 위치를 가리킵니다. 이 식을 이해하기 위해서는 (코)사인 함수의 그래프를 생각해보면 되는데,

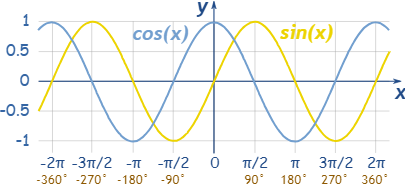
예를 들어 1번 차원의 첫 임베딩 벡터에는 $PE(1,2)=sin(1/10000^{2/512})$ 의 값이 더해집니다. 1번 차원의 두 번째 임베딩 벡터에는 $PE(2,2)=sin(1/10000^{2/512})$ 값이 더해지겠죠? 반대로 2번 차원의 첫 임베딩 벡터에는 $PE(1,3)=cos(1/10000^{4/512})$ 의 값이 더해지고, 두 번째 임베딩 벡터에는 $PE(2,3)=cos(1/10000^{4/512})$ 값이 더해질 것입니다.

이런 식으로 $d_{model}$ 크기만큼 (코)사인함수를 쪼개어 각 값을 더해주면 각 임베딩 벡터의 고유한 positional information이 sequential하게 인코딩될 수 있습니다. 즉, 같은 단어라도 위치가 달라지면 positional encoding 값이 바뀌어 다른 벡터로 취급하게 됩니다. 또한 (코)사인 함수는 같은 모양이 반복되는 형태이기 때문에 혹여나 학습에 사용한 시퀀스 데이터보다 더 긴 데이터가 들어오더라도 positional encoding을 쉽게 적용할 수 있습니다.

Attention

Positional encoding을 거친 임베딩 벡터는 attention 모듈에 입력됩니다.

Attention은 Query 벡터를 Key, Value 벡터 쌍에 매칭하는 일을 합니다. Attention 모듈의 출력값 역시 벡터이며, 내부적으로는 scaled dot product 여러 개가 병렬로 구성된 multi head attention 구조를 가지고 있습니다. 그림으로 보면 다음과 같습니다.

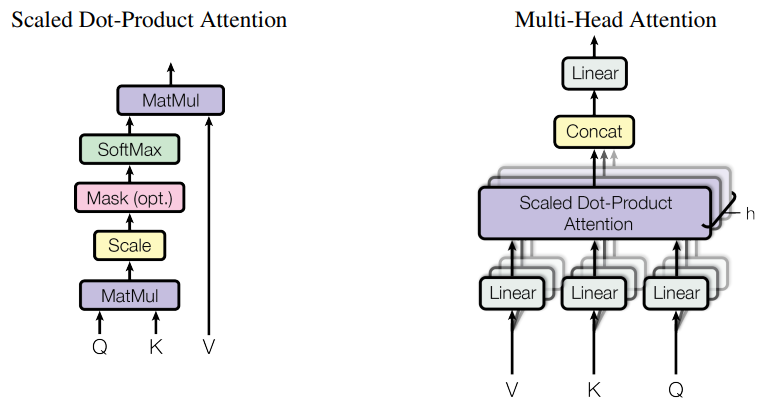
Attention 모듈은 scaled dot product라는 이름처럼 내부적으로 query와 key를 내적하고 스케일링하는 과정을 거칩니다. 이렇게 구한 값을 softmax에 넣어서 Value의 weight로 삼는데, 이는 곧 query에 대한 데이터(value)의 연관도(에 비례하는 값)를 가중치로 사용하는 것입니다.

\text{Attention}(Q, K, V)=\text{softmax}\left({QK^T\over \sqrt{d_v}}\right)V\qquad(1)

Multi Head Attention

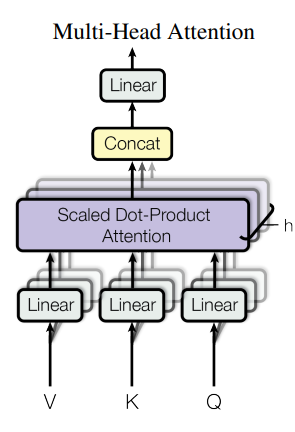
Multi head attention이라는 표현은 따로 특별한 모듈을 지칭하는 것이 아니고 $h$ 개의 어텐션을 거쳐 나온 결과를 합쳐서 FC layer로 넘기는 과정을 말합니다.

이 때 $K, Q$ 벡터의 차원을 $d_k$ , $V$ 벡터의 차원을 $d_v$ 라고 하면 $d_{model}/h=d_k=d_v$ 의 크기를 갖습니다. (디폴트 값은 $h=8, d_{model}=512, d_k=d_v=64$ 입니다.)

예를 들어 $d_{model}$ 크기를 갖는 임베딩 벡터 $x_e$ 가 주어졌다면, $x_e$ 를 $h\times3$ 개의 linear layers에 넣어 $d_k=d_v$ 차원을 갖는 벡터 $3h$ 개를 생성합니다. 생성된 $3h$ 개의 $Q,K,V$ 벡터들은 다시 각 head에 입력되어 $d_k=d_v$ 크기의 출력 벡터 $h_i$ 가 되고, 각각의 출력을 모두 concat한 값이 muli head attention의 최종 출력이 되는 것이죠.

이상의 과정을 식으로 나타내면 다음과 같습니다.

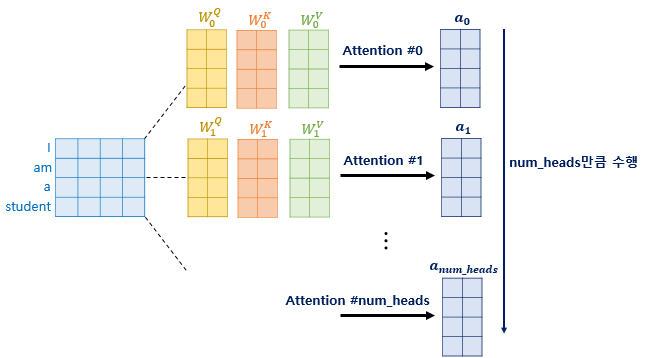
h_i=\text{Attention}(Q_iW^Q_i, K_iW^K_i, V_iW^V_i)\\ \quad\\ \text{Multi-head}(Q, K, V)=\text{Concat}(h_1, h_2, \cdots,h_h)W^O

여기서 각각의 $K,Q,V$ 가 맥락상 어떤 의미를 갖는지 이해하는 것이 중요합니다. 이에 대해서는 먼저 scaled dot product attention과 self attention을 살펴본 후 다시 설명하겠습니다.

Scaled Dot Product Attention

이름에서 알 수 있듯이 원래 dot product attention에는 scaling하는 과정이 없습니다. 여기서 scaling을 진행하는 이유는 key와 query의 차원 크기가 커질수록 내적값이 커지기 때문입니다.

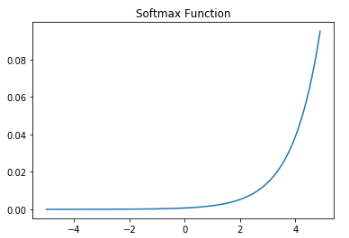
Softmax 함수는 위와 같은 모양을 갖는데 입력값이 지나치게 커지면 기울기의 변화가 거의 없는 구간으로 진입하게 됩니다. 그래디언트 관점에서 기울기의 변화가 거의 없다는 것은 그래디언트가 0에 가깝다는 것을 의미합니다. 문제는 softmax의 그래디언트가 각 확률의 곱으로 표현된다는 점입니다.

$x, y, z$ 3개의 변수가 있다고 가정했을 때 softmax 함수를 각각에 대해 미분하면 다음과 같습니다.

\begin{bmatrix} \sigma(x)(1-\sigma(x)) & -\sigma(x)\sigma(y) & -\sigma(x)\sigma(z) \\ -\sigma(x)\sigma(y) & \sigma(y)(1-\sigma(y)) & -\sigma(y)\sigma(z) \\ -\sigma(x)\sigma(z) & -\sigma(y)\sigma(z) & \sigma(z)(1-\sigma(z)) \end{bmatrix}

이처럼 softmax의 그래디언트는 각 변수의 확률의 곱이기 때문에 그래디언트가 0에 가깝다면 어떤 한 변수의 영향력이 점차 사라지는 gradient vanishing이 발생하게 됩니다.

Query와 Key의 $i$ 번째 요소를 $q_i, k_i$ 로 놓고 각 값이 $\text{i.i.d}\sim N(0,1)$ 을 따른다면 $q_ik_i$ 의 분산은 다음과 같습니다.

\begin{aligned} E[q_ik_i]&=E[q_i]E[k_i]=0,\\ \quad\\ Var[q_ik_i]&=E[q_i^2k_i^2]-E[q_ik_i]^2=E[q_i^2]E[k_i^2]\\ \quad\\ &=(Var[q_i]-E[q_i]^2)(Var[k_i]-E[k_i]^2)=1,\\ \quad\\ \therefore&\sum_{i=1}^{d_k}q_ik_i\sim N(0, d_k)\\ \end{aligned}

따라서 $\sqrt{d_k}$ 로 scaling을 해 주면 $Q,K$ 를 내적한 벡터의 각 요소는 softmax에 넣었을 때 기울기가 0이 아닌 구간에 위치할 확률이 높아지게 됩니다. Softmax는 각 확률변수의 실제 값이 아니라 비례 관계가 중요한 함수이기 때문에 스케일링해도 가중치의 역할이 달라지지 않습니다.

Position-wise Feed-Forward Network

Attention 모듈을 모두 거쳐 최종적으로 출력된 output 벡터는 position wise feed forward network에 입력됩니다. 이름이 길지만 간단하게 말하면 그냥 input 데이터의 각 위치마다 Fully Connected layer를 적용하는 것입니다. 수식으로 나타내면 다음과 같습니다.

\text{FFN}=\max(0, xW_1+b_1)W_2+b_2

여기서 $x$ 는 attention 모듈의 출력 벡터입니다. 활성화 함수로는 ReLU를 사용합니다. ( $\max$ ()). 첫 번째 레이어는 $d_{ff}=2048$ 의 차원을 가지며, 최종적으로 입력과 동일한 $d_{model}=512$ 크기의 벡터가 출력됩니다.

Self attention과 Q, K, V의 역할

논문에서 언급하는 attention 모듈은 기본적으로 self attention입니다.

식 (1)을 보면 attention 모듈은 $Q,K,V$ 벡터를 입력받아 $Q,K$ 의 내적을 수행합니다. 이 때 $Q,K,V$ 는 모두 동일한 input vector $x$ 에서 나온 벡터들입니다. 이렇게 보면 $Q,K$ 를 내적하는 것이 이상하게 느껴집니다. 왜냐하면 $Q$ 와 $K$ 는 같은 데이터를 다르게 사영했을 뿐인 일종의 '형제 벡터'이기 때문이죠. 형제끼리 얼마나 비슷한지를 보는 것이 도대체 무슨 의미가 있을까요?

여기서 softmax 함수가 등장합니다. 두 형제 벡터의 유사도가 높은 부분일수록 softmax 연산의 결과값이 높게 나오는데, 이 값이 마지막 형제 벡터인 $V$ 의 가중치가 됩니다.

import torch.nn.functional as F
import torch

aa = torch.Tensor([0.1, 0.3, 0.6])
bb = torch.Tensor([0.2, 0.5, 0.3])
print(F.softmax(aa, dim=-1))
print(F.softmax(bb, dim=-1))

>>>tensor([0.2584, 0.3156, 0.4260])
>>>tensor([0.2894, 0.3907, 0.3199])

즉, $Q,K$ 가 유사할수록 $V$ 벡터가 결과에 더 크게 반영됩니다. (각각의 벡터값은 오차역전파를 통해 자연스럽게 보정되므로 해당 값이 실제로 유의미한지를 따질 필요는 없습니다.)

최종적으로 $V$ 는 실제 input data의 representation 역할을 하게 되며, $Q,K$ 의 내적값은 문장에서 각 원소가 가지는 중요도를 가중치로 나타낸 것이 되는데 이를 문장 전체의 관점에서 보면 일종의 문장 내 의미적 맥락의 분포로 해석할 수 있습니다. 단순히 임베딩 벡터를 구하는 것이 아니라 일단 구한 임베딩을 일종의 데이터베이스로 취급하여 검색과 매칭 기능까지 갖춘 구조로 바꾸고 이를 업데이트하는 셈입니다. 실로 기똥찬 발상이죠!

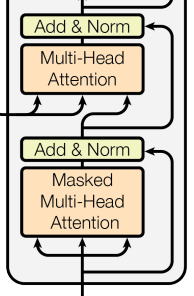
디코더에서 self attention 위에 일반 attention이 오는 이유도 여기서 기인합니다. 해당 attention 모듈에 들어가는 $K$ 와 $V$ 는 인코더에서, $Q$ 는 디코더에서 전달받는데 이는 "디코더에서 사용하는 의미적 맥락에 적합한 인코더의 Key-Value 쌍은 무엇인가?"를 학습하는 것입니다. 예컨대 트랜스포머를 사용한 번역기는 인코더에서 다루는 언어와 디코더에서 다루는 언어 간의 의미적 맥락을 매칭시킬 수 있게 됩니다.

트랜스포머의 확장성은 바로 여기서 나옵니다. 번역기를 예시로 들었지만 실제로 트랜스포머가 다루는 것은 데이터이고, 이 말인 즉슨 무엇이든 벡터 데이터로 변환할 수 있다면 서로 다른 의미적 맥락을 가지는 데이터를 서로 매칭시킬 수 있다는 뜻이 되기 때문입니다.

Limitations

다재다능한 트랜스포머도 물론 단점이 있습니다.

사실상 모든 트랜스포머 기반 모델이 공유하는 단점인데, 바로 막대한 메모리 사용량과 computational cost입니다. 특히 self attention layer의 계산복잡도는 $O(n^2)$ 으로 알고리즘 중에서도 꽤나 큰 편에 속합니다. 만약 input sequence 길이가 2048이라면 최소 4,194,304의 연산이 필요하며, 연산당 0.02ms가 걸린다고 가정하면 계산을 끝내는 데 약 83초가 걸립니다. (물론 실제론 이 정도로 오래 걸리진 않습니다.)

게다가 유의미한 성능을 이끌어내려면 타 모델보다 훨씬 많은 데이터가 필요한데 그조차도 underfitting되는 경우가 잦습니다. 대표적으로 BERT는 2023년 8월 기준으로 적절한 환경에서 약 1시간 이내에 훈련을 완료할 수 있지만, 처음 발표되었을 당시에는 학습과 파인튜닝에만 며칠 이상의 시간이 소요되었습니다. 그럼에도 불구하고 underfitting의 징후가 여럿 포착되어 RoBerta 같은 모델이 만들어지기도 했는데, 이처럼 트랜스포머 기반의 구현체는 자원 소모와 활용 측면에서 지나치게 무거운 경향이 있습니다. '소 잡는 칼'인 셈이죠.

참고문헌

Ethan

재미있게 살고 싶은 대학원생

이전 포스트

[Vision] Generative Adversarial Nets (GAN)

다음 포스트

[딥러닝] Layer Collaboration in the Forward-Forward Algorithm

1개의 댓글

happy

2023년 8월 12일

유익한 글이었습니다.

답글 달기