[Vision] Generative Adversarial Nets (GAN)

Ethan·2023년 7월 29일

CV Generative Adversarial Network gan

Papers Review

목록 보기

12/18

본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용/오류 지적이나 추가 의견은 댓글로 남겨주시면 감사하겠습니다.

Published in NIPS 2014

Summary

Generator와 Discriminator 간의 경쟁을 통해 모델이 생성하는 데이터의 퀄리티를 향상시키는 Adversarial nets 제안
범용성은 뛰어나지만 학습이 불안정하고 mode collapse 문제 존재

What's new and work importance

이안 굿펠로우가 박사 과정 때 쓴 유명한 논문입니다. Generative Adversarial Nets는 Generator, Discriminator 두 개의 모듈이 상호 경쟁하며 출력의 퀄리티를 높이도록 유도하는 구조를 말합니다. 확장성이 매우 좋고 구현이 간단하여 여러 분야에서 활발하게 사용되고 있습니다. 복잡한 approximate inference (대표적으로 Variational Inference)가 필요 없다는 것도 장점입니다.

Background

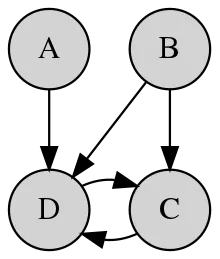
변수 간의 상호 의존 관계를 표현한 확률 모델을 Graphical model이라고 합니다. 자료구조에서 다루는 그 그래프에서 따온 표현인데, Markov chain처럼 conditional probability를 사용해서 변수 간의 관계를 나타내고자 하는 시도입니다. GNN도 graphical model의 일종이죠.

일반적으로 sample generation을 위해 graphical model을 쓰게 되면 구조상 markov chain 같은 방식을 활용해야 한다는 문제가 있습니다.

이를 피하기 위해 Score matching이나 Noise Constrastive Estimation (NCE) 같은 alternative criterion을 사용할 수도 있지만, 둘 다 normalization constant를 포함한 probability density를 알아야 합니다. 일반적으로 latent variable이 존재하는 approximate inference 기반의 모델에서는 다루기 쉬운 unnormalized probability density를 구하는 것조차 불가능한 경우가 많기 때문에 generative model에서 이러한 criterion을 사용하기가 상당히 불편하죠.

물론 2023년 현재에는 graphical model이 아니더라도 상당한 퀄리티의 데이터를 생성하는 모델들이 많지만, 2014년에는 그러한 모델들이 존재하지 않거나 보편화되지 않았습니다. 이러한 맥락에서 GAN은 기존 모델들보다 더 간단하면서도 강력한 생성 능력을 선보였고 많은 각광을 받아 후속 연구들이 쏟아져 나오게 됩니다.

Model Architecture

자 그러면 이제 GAN의 구조를 살펴보겠습니다.

먼저 Generator와 discriminator 모두 MLP일 때를 가정해 봅시다.

데이터 $x$ 를 입력받은 generator의 분포 $p_g$
input (gaussian) noise variables에 대한 prior $p_z(z)$
generator $G(z;\theta_g)$
discriminator $D(x;\theta_d)$

$G$ 는 미분가능한 함수이고 $D$ 는 단일 스칼라를 출력하는 mlp layer입니다. $D(x)$ 는 주어진 input $x$ 가 generator에서 만들어낸 분포 $p_g$ 가 아니라 실제 데이터 $x$ 에서 샘플링되었을 확률을 의미합니다.

\min_G\max_D V(D, G) = \mathbb{E}_{x\sim p_{data}(x)} [\log D(x)]+\mathbb{E}_{z\sim p_z(z)}[\log(1-D(G(z)))]\qquad (1)

위 식에서 우변의 첫 항은 discriminator에 real data가 주어졌을 때 real data로 판별할 확률에 대한 기댓값이고, 두 번째 항은 generator가 생성한 fake data가 주어졌을 때 real data라고 판별하지 않을 확률에 대한 기댓값입니다. 즉, $D$ 입장에서는 1항과 2항을 모두 최대화하는 것이 학습 목표가 됩니다. 반대로 $G$ 입장에서는 2항을 최소화하는 것이 목표가 되겠죠.

식 (1)을 먼저 discriminator의 관점에서 살펴보겠습니다. Discriminator는 다음의 2가지 사항을 고려해야 합니다.

maximize $D(x)$ : real data를 real data로 잘 판별함
minimize $D(G(z))$ : fake data를 fake data로 잘 판별함

만약 discriminator가 모든 데이터를 구분할 수 있다면 $\log D(x)=1,\ \log D(G(z))=0$ 이 되어 $V(D, G)=0$ 가 됩니다. 반대로 아무것도 구분하지 못한다면 $\log D(x)=0,\ \log D(G(z))=1$ 이 되어 $V(D, G)=-\infty$ 가 되겠죠. 따라서 discriminator는 $V(D, G)$ 를 최대화하는 방향으로 학습이 진행되어야 합니다. 이를 수식으로 나타내면 다음과 같습니다.

\max_D V(D, G)=\mathbb{E}_{x\sim p_{data}(x)}[\log D(x)]+\mathbb{E}_{z\sim p_z(z)}[\log(1-D(G(z)))]\qquad (2)

반대로 Generator는 discriminator와 달리 real data를 고려할 필요가 없습니다. Generator 입장에서 유일한 관심사는 생성한 fake data가 discriminator를 얼마나 잘 속일 수 있느냐이기 때문입니다. 만약 generator가 생성하는 fake sample이 전혀 효과적이지 못하다면 $D(G(z))=0$ 이 되고, 매우 효과적이라면 $D(G(z))=1$ 이 되겠죠. 따라서 generator는 $V(D, G)$ 를 최소화해야 합니다. 결과적으로 generator의 objective function은 다음과 같습니다.

\min_G V(D, G)=\mathbb{E}_{z\sim p_z(z)}[\log(1-D(G(z)))]\qquad (3)

최종적으로 식 (2)와 (3)을 합친 게 식 (1)이 됩니다.

그런데 현실적으로 computational cost와 data size의 한계 때문에 약간의 변형이 필요합니다. 논문에서는 아래와 같이 $k$ 번 $D$ 를 최적화한 후 $G$ 를 1번 최적화하는 식으로 진행했습니다. 이렇게 하면 $G$ 가 천천히 수렴하는 동안 $D$ 가 optimal solution 근처에 머물게 된다고 합니다. $D$ 의 학습 속도를 적당히 조절해서 $G$ 와 균형을 맞추는 것입니다.

또다른 현실적인 문제는 학습 초기에 $G$ 가 생성하는 데이터의 퀄리티가 낮아서 학습을 방해한다는 점입니다. 즉, generator가 생성하는 데이터를 잘 구분할 수 있어서 $D(G(z))$ 의 초기 값이 0에 가까우면 $\log(1-D(G(z)))$ 의 gradient가 작은 값이 나오기 때문에 학습 속도가 매우 느려집니다. 그래서 차라리 $-\log D(G(z))$ 를 최대화하는 방향으로 $G$ 를 학습시키는 것이 효율적입니다. 두 방법은 동일한 결과를 얻게 되지만 초기 학습에는 후자가 훨씬 유리하죠.

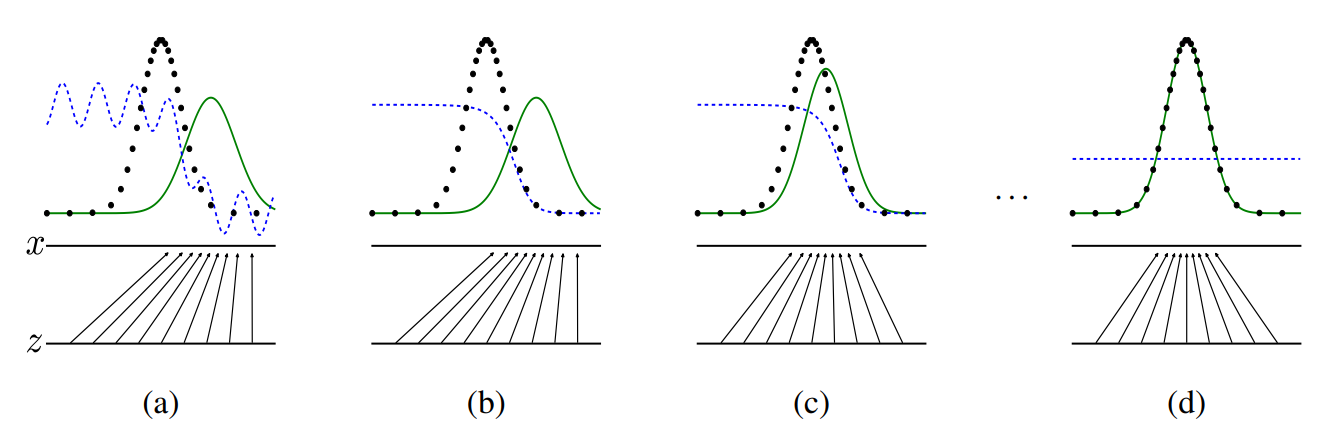
위 그림에서 파란색은 discriminator의 분류 결과, 초록색 실선은 generator가 생성한 fake data의 분포, 검은색 점선은 실제 데이터 $x$ 의 분포를 나타냅니다. (a)를 보면 처음에는 fake와 real data가 매우 큰 차이를 보이기 때문에 쉽게 구분을 해내지만, 학습이 진행되면서 generator가 real data를 모사하기 시작하면 점점 더 real data와 fake data를 구분하지 못해 $D(x)$ 값이 내려가게 되고, 최종적으로는 가짜와 진짜를 전혀 구분하지 못해 $D(x)$ 값이 1/2에 도달하게 됩니다.

Theoretical Analysis

Global Optimality

만약 generator $G$ 가 잘 학습되었다면 noise $z$ 를 입력받아 생성한 데이터의 분포 $p_g$ 는 $p_{data}$ 와 같을 것입니다. 이러한 $G$ 를 이미 얻었다고 가정하면, 이 때 $G$ 에 맞게 최적화된 discriminator $D^*$ 는 다음과 같습니다.

\begin{aligned} D^* &= \max_D V(D, G)\\ \quad\\ &= \mathbb{E}_{x\sim p_{data}(x)} [\log D(x)]+\mathbb{E}_{z\sim p_z(z)}[\log(1-D(G(z)))]\\ \quad\\ &= \mathbb{E}_{x\sim p_{data}(x)} [\log D(x)]+\mathbb{E}_{x\sim p_g(x)}[\log(1-D(x))]\\ \quad\\ &= \int_xp_{data}(x)\log D(x)dx + \int_xp_g\log(1-D(x))dx\\ \quad\\ &= \int_xp_{data}(x)\log D(x) + p_g\log(1-D(x))\ dx\qquad(4) \end{aligned}

식 (4)가 최대화되려면 $D(x)$ 로 미분한 값이 0인 지점을 찾으면 됩니다. $p_{data}=a,\ p_g=b,\ D(x)=y$ 로 놓으면 다음과 같이 나타낼 수 있습니다.

{\partial\over \partial y}(a\log y+b\log(1-y)) = {a\over y}-{b\over (1-y)} = 0

즉 $y={a\over a+b}$ 일 때 최대값을 가지므로,

D^*(x)={p_g(x)\over p_{data}(x)+p_g(x)}\qquad (5)

가 됩니다. 이 때 $p_g=p_{data}$ 이므로 $D^*(x)=1/2$ 이 되죠.

이번에는 반대로 최적의 discriminator $D$ 가 주어졌다고 가정해봅시다. 그러면 최적의 generator $G^*$ 는 다음과 같습니다.

\begin{aligned} G^* &= \min_GV(D^*, G)\\ \quad\\ &= \int_xp_{data}(x)\log D^*(x) + \int_xp_g(x)\log(1-D^*(x))dx\\ \quad\\ &= \int_xp_{data}(x)\log \left({p_{data}(x)\over p_{data}(x)+p_g(x)}\right)dx + \int_xp_g(x)\log\left({p_g(x)\over p_{data}(x)+p_g(x)}\right)dx\\ \quad\\ &=-\log4+\log4+\int_xp_{data}(x)\log \left({p_{data}(x)\over p_{data}(x)+p_g(x)}\right)dx + \int_xp_g(x)\log\left({p_g(x)\over p_{data}(x)+p_g(x)}\right)dx\\ \quad\\ &=-\log4+\int_xp_{data}(x)\log \left({2\cdot p_{data}(x)\over p_{data}(x)+p_g(x)}\right)dx + \int_xp_g(x)\log\left({2\cdot p_g(x)\over p_{data}(x)+p_g(x)}\right)dx\\ \quad\\ &= -\log4+\int_xp_{data}(x)\log \left({p_{data}(x)\over {p_{data}(x)+p_g(x)\over 2}}\right)dx + \int_xp_g(x)\log\left({p_g(x)\over {p_{data}(x)+p_g(x)\over2}}\right)dx\\ \quad\\ &= -\log4+\int_xp_{data}(x)\log \left({p_{data}(x)\over {p_{data}(x)+p_g(x)\over 2}}\right)dx + \int_xp_g(x)\log\left({p_g(x)\over {p_{data}(x)+p_g(x)\over2}}\right)dx\\ \quad\\ &= -\log4+KL\left(p_{data}(x)||{p_{data}(x)+p_g(x)\over2}\right)+KL\left(p_g(x)||{p_{data}(x)+p_g(x)\over2}\right)\\\quad\\ &= -\log4+2\cdot JS(p_{data}(x)||p_g(x)) \end{aligned}

즉, 최적의 discriminator $D$ 가 주어졌을 때 generator $G$ 를 최적화하는 과정은 $p_{data}$ 와 $p_g$ 의 JS Divergence를 최소화하는 것과 같습니다. 다시 말해 $G$ 는 생성하는 데이터가 실제 데이터와 최대한 유사하도록 학습이 진행된다는 의미입니다.

Convergence of Algorithm

이번에는 모델의 학습 능력에 대해 살펴보겠습니다.

어떤 함수 $f(x)=\sup_{\alpha\in A}f_\alpha(x)$ 이고 $f_\alpha(x)$ 가 모든 $\alpha$ 에서 convex하다면, $\beta=\arg\sup_{\alpha\in A}f_\alpha(x)$ 일 때 $\partial f_\beta(x)\in \partial f(x)$ 가 성립합니다.

제대로 학습이 진행되었다면 GAN의 objective function $V(D, G)=U(p_g,D)$ 가 되는데, $U$ 는 $p_g$ 에 대해 convex하므로 $\sup_D U(p_g, D)$ 도 당연히 $p_g$ 에 대해 convex합니다. 따라서 gradient descent를 사용하여 $p_g$ 를 업데이트하다보면 optimal point $p_x$ 에 도달할 수 있습니다.

현실적으로 모델은 한정된 데이터를 가지고 학습을 해야 하고, $p_g$ 를 바로 업데이트하는 것이 아니라 $G(z;\theta_g)$ 를 통해 $\theta_g$ 를 업데이트하기 때문에 이론적으로는 찾아낸 파라미터 $\theta_g^*$ 가 optimal solution $p_x$ 를 완벽하게 나타내지 못할 수도 있습니다. (논문에서는 parameter space 내 critical points에 부딪힌다고 표현합니다.)

Experiments

MNIST와 Toronto Face Database (TFD), CIFAR-10 데이터셋을 사용하여 실험을 진행했습니다. generator는 relu와 sigmoid를 activation function으로 사용하였고, discriminator는 maxout을 사용하여 학습시켰습니다. 이론적으로 generator 어디든 noise를 추가하거나 dropout을 적용할 수 있지만 논문에서는 generator의 최하단 layer에 입력으로 noise를 넣어주었습니다.

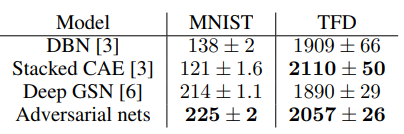
위 표는 generator가 생성한 데이터에 Gaussian Parzen window를 적용하여 $p_g$ 와 test data의 분포를 비교하고, 이에 대한 log likelihood를 추정한 결과입니다. 쉽게 말해서 generator가 생성한 데이터와 test data의 유사도를 비교해봤다는 의미입니다.

표를 보면 baseline 대비 GAN의 log likelihood가 더 높습니다. 즉, 다른 모델들에 비해 test data를 더 잘 근사했다고 할 수 있습니다.

각각의 데이터셋에 대한 실험 결과입니다.

재현된 그림을 보면 알겠지만 사실 original GAN이 생성하는 결과물의 퀄리티가 그리 좋은 편이 아닙니다. 논문에서도 이 점에 대해서는 부정하지 않습니다. 논문 공개 당시에는 GAN이 일종의 preliminary research 였기 때문입니다.

Advantages and limitations

GAN의 치명적인 단점 중 하나는 학습 과정이 상당히 불안정하다는 것입니다. Generator가 근사하는 데이터의 분포 $p_g(x)$ 에 대한 명확한 representation이 따로 있는 게 아니기 때문에 $G$ 와 $D$ 의 학습 균형을 잘 맞춰야 하는데, original GAN에서는 이게 꽤 까다로운 문제였습니다.

이로 인해 발생하는 대표적인 문제가 mode collapse입니다. Helvetica scenario라고도 하는데, generator $G$ 의 학습 속도가 discriminator $D$ 보다 지나치게 빠르면 $G$ 는 $D$ 를 잘 속이는 특정한 데이터 포인트 또는 manifold에 치중하게 되어 해당 데이터만 지속적으로 생성하는 현상을 말합니다. Latent space의 관점에서 보자면 서로 다른 $z$ 를 계속해서 유사한 output으로 매핑하는 것이죠.

Mode collapse는 generator의 학습 기준이 discriminator에 맞춰져 있기 때문에 발생하는 문제입니다. 쉽게 말해서 generator의 목적이 좋은 데이터를 생성하는 것이 아니라 discriminator를 속이는 것이기 때문에 이런 현상이 나타나는 것입니다. 흔히 '생성 모델'이라고 하면 다양한 데이터를 생성하는 능력을 가지고 있다고 생각하지만, 이런 이유로 GAN은 사실 '다양한 데이터를 생성하는' 능력은 없습니다. 식 (1)을 보면 data의 diversity를 고려하는 항이 없다는 걸 알 수 있죠.

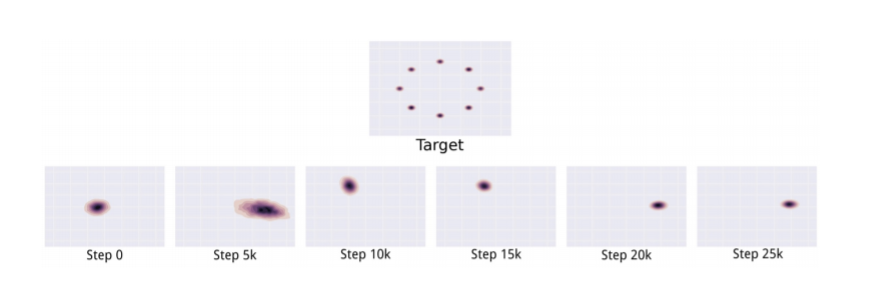
일반적으로 완전한 mode collapse보다는 부분적인 mode collapse가 잘 일어난다고 합니다. 위 그림을 보면 유사한 특정한 target point 근처의 데이터만 생성하고 있는데요. 일종의 local minimum problem으로, generator와의 학습 속도 차이로 인해 한 번 속기 시작한 discriminator가 판별 능력을 회복하기 쉽지 않기 때문에 min-max game의 주도권이 generator에 넘어가 버리는 것입니다.

그래서 일반적으로 $G$ 를 제대로 학습시키는 것이 $D$ 를 학습시키는 것보다 훨씬 어렵습니다. 흔히 vanilla GAN 학습이 어렵다는 이야기는 주로 이런 의미입니다.

현재까지 알려진 Mode collapse를 해결하는 효과적인 방법 몇 가지는 다음과 같습니다.

feature matching : fake와 real data의 least square error 항을 loss function에 추가

mini batch discrimination : 미니배치 단위로 fake와 real data 사이 거리의 합의 차이를 loss function에 추가

historical averaging : 배치 단위로 파라미터를 업데이트하면 이전 배치의 영향력이 줄어드므로, 이전 학습 내용을 기억하는 방식으로 학습을 진행

참고문헌

Ethan

재미있게 살고 싶은 대학원생

이전 포스트

[Vision] MLP-Mixer: An all-MLP Architecture for Vision

다음 포스트

[NLP] Attention Is All You Need (Transformer)

3개의 댓글

happy

2023년 7월 29일

이런 유용한 정보를 나눠주셔서 감사합니다.

답글 달기

최원석

2023년 10월 15일

안녕하세요 글 잘 보고 있어요..!
제가 요즘 많이 고심하는데도 모르겠어서
여쭤보고 싶은 공업수학 문제가 있는데
혹시 답변 해주실 수 있으실까요..?
곤란 하시다면 답변 안 해주셔도 괜찮아요
문제는 이거예요…!

“분리가능 상미분 방정식은 양형태 상미분 방정식의 일부이고, 완전 상미분 방정식은 음형태 상미분 방정식 일부라고 볼 수 있다.
양형태의 상미분 방정식 중 분리가능한 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 분리가능하지 않은 상미분 방정식들), 음형태의 상미분 방정식 중 완전 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 완전하지 않은 상미분 방정식들) 쓰시오.
즉.
양형태의 상미분 방정식의 전체 집합을 W.
음형태의 상미분 방정식의 전체 집합을 U,
분리가능한 상미분 방정식의 전체 집합을 A,
완전 상미분 방정식의 전체 집합을 B
라고 할 때
집합 A^c ᑎ W 과 집합 B^c ᑎ U 에 대해 기술하는 문제이다. 그 집합에 해당하는 미분 방 정식의 예를 몇 개 구하고 그들의 공통된 특징을 기술하는 방법을 써도 좋고, 아니면 이 집 합에 속하는 방정식들의 특징을 바로 기술하여도 좋다.“

1개의 답글