모든 Paper review는 제가 공부하고 남기는 기록입니다.
잘못된 내용이나 추가 의견이 있으시면 언제든 자유롭게 댓글 남겨주세요.

Published: UAI, 2018
Paper: https://arxiv.org/abs/1803.05407

---

[요약]

• FGE(Fast Geometric Ensembling) 대비 더 좋은 성능과 효율적인 학습이 가능한 SWA(Stochastic Weight Averaging)를 제안했습니다.

• SWA는 SGD의 학습 과정에서 weight를 averaging함으로써 Flatter solution을 얻을 수 있고, SGD보다 local optimum surface의 중심부로 접근할 수 있습니다.

• SWA는 SGD보다 wider solution을 얻어 generalization 성능을 증가시킬 수 있습니다.

---

[서론]

Abstract

• SGD를 사용할 때, 학습 과정에서 여러 개의 지점들을 평균내면 더 좋은 generalization 성능을 얻을 수 있다는 논문입니다.

• SWA을 사용하면 SGD를 쓰는 것보다 flatter solution을 얻을 수 있고, FGE을 한 개의 모델만으로 근사할 수 있다고 합니다.

Introduction

• 선행연구에서 SGD가 찾는 local optima는 near constant loss curves로 연결된다는 것을 보였습니다.

• 여기서 아이디어를 얻은 FGE는 학습 과정에서 weight space 근처의 여러 지점을 sampling하여 ensemble하는 방법입니다. 선행 연구로 Snapshot Ensemble이 있습니다.

• 선행 연구들로 미루어 볼 때, weight space에서 ensemble을 실행하는 것이 model space에서 실행하는 것보다 더 promising하다고 합니다.

• SWA는 다음과 같은 장점들을 가지고 있습니다.

  (1) SGD보다 central points of optimal set에 더 가까이 접근할 수 있습니다. (= Flatter solution)

  (2) 단일 모델로도 FGE를 근사할 수 있습니다. (FGE는 ensemble 과정에서 k개의 모델을 필요로 함)

  (3) SGD보다 더 넓은 범위의 solution을 찾아냅니다. width of optima는 generalization 성능과 밀접한 관계가 있습니다.

[본론]

Related work

• SWA를 더 잘 이해하기 위해 Snapshot Ensemble(SSE)과 FGE를 먼저 짚고 넘어가겠습니다.

Snapshot Ensemble (SSE)

• SSE의 핵심은 Cyclical learning rate (e.g. Cosine Annealing)을 사용함으로써 다양한 관점(diverse prediction)을 학습한 단일 모델을 얻을 수 있다는 것입니다.

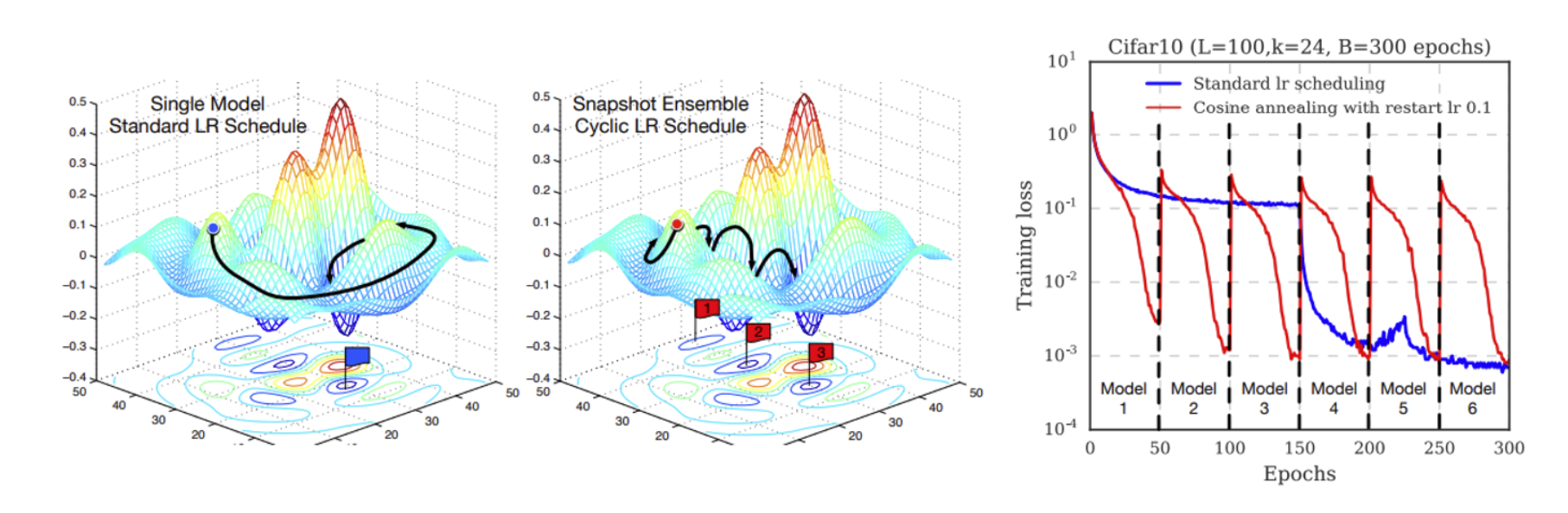
• 위 그림을 보면 cyclical lr을 사용하는 모델은 여러 개의 local optima에 도달할 수 있고, 각각의 local optima를 ensemble하고 있습니다.

Fast Geometric Ensembling (FGE)

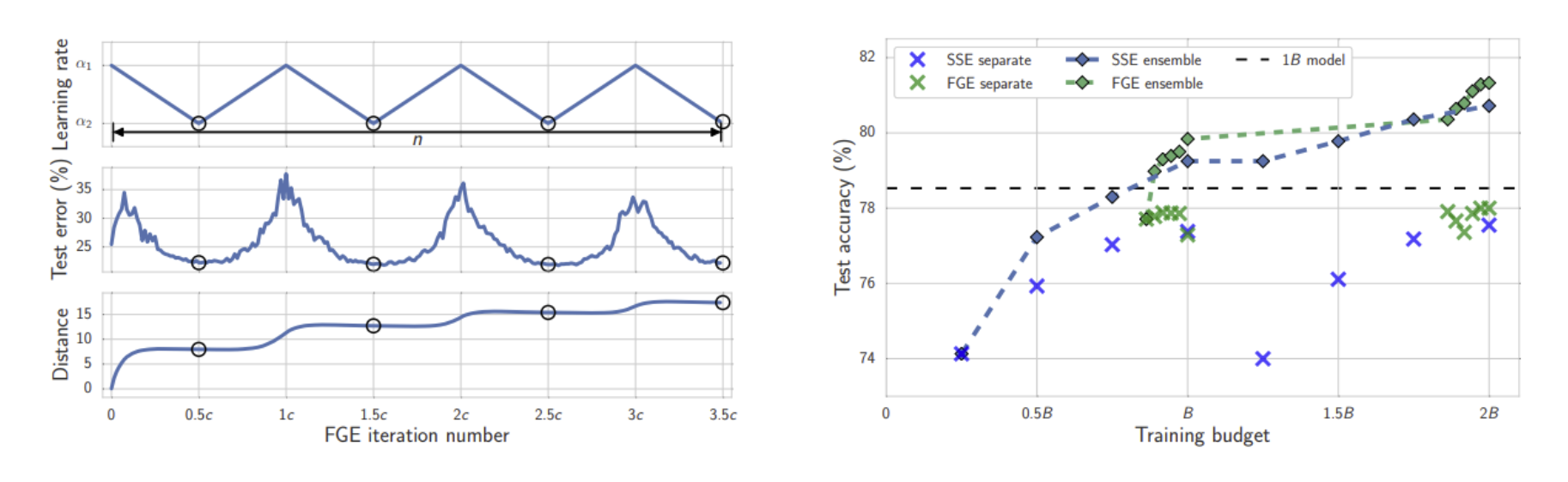
• FGE는 SSE와 달리 piecewise linear cyclical learning rate를 사용하며 cycle 주기도 더 빠르고, SSE보다 더 빠르게 좋은 모델을 찾는다고 합니다.

주1:
아직 FGE 논문을 읽지는 않았지만, 설명을 보면 cosine annealing만 사용하지 않고 cycle마다 learning rate를 다분화해서 사용한다는 의미로 보입니다.

Stochastic Weight Averaging (SWA)

Analysis of SGD Trajectories

• SWA는 SGD에 cyclical & constant learning rate를 사용하여 고성능을 낼 수 있는 optimal region을 탐색하면서 샘플링한 weights의 평균을 구하는 메커니즘이라고 합니다.

  쉽게 얘기해서, SGD에 learning rate scheduling을 적용하여 수렴하는 도중에 local optimum 근처에 도달했을 때, 학습 지점들의 weight를 평균내면 optimal solution에 더 가까이 갈 수 있다는 뜻입니다.

• iteration $i$, learning rate $\alpha$, cycle length $c$에 대해 다음과 같습니다. 각각의 파라미터는 학습이 가능합니다.

  $\alpha(i)=(1-t(i))\alpha_1+t(i)\alpha_2$

  $t(i)={1\over c}(\mathrm{mod}(i-1, c)+1)$

• 논문에서는 discontinuous learning schedule을 사용합니다. 기존의 cycling 방식과 달리 천천히 learning rate를 증가시키는 대신, minimum에서 maximum으로 바로 점프합니다. 또는 $\alpha_i=\alpha_1$인 constant learning rate를 사용하기도 합니다.

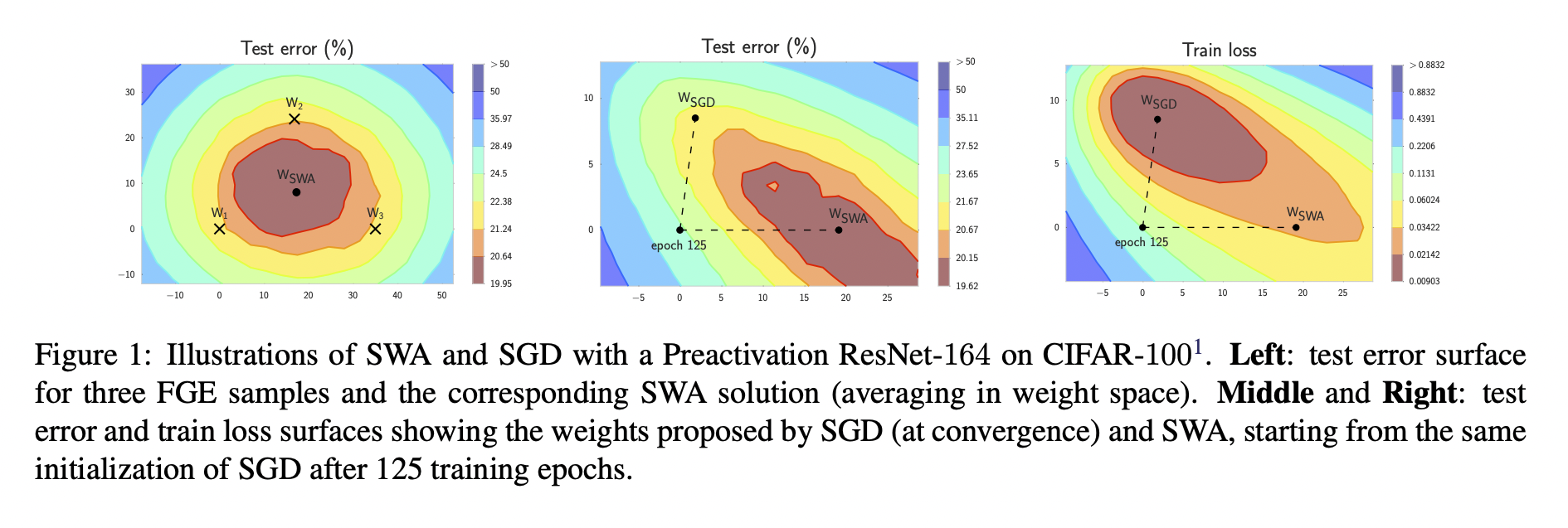
• 위 그림은 SWA와 FGE의 학습 과정을 비교한 것입니다. 딱 봐도 SWA가 더 optima에 가깝게 수렴하고 있죠? SWA의 train loss가 SGD보다 높지만, test error는 더 낮은 것도 확인할 수 있습니다.

SWA Algorithm

• SWA의 알고리즘은 위와 같습니다.

  $\hat w$ = pretrained model
  $B$ = 주어진 모델을 기존의 방법으로 학습하는데 필요한 epoch 수
  $w_i$ = minimum 또는 constant lr일 때의 모델 가중치
  $w_{\mathrm{swa}}$ = $w_i$들을 평균낸 최종 값

Computational Complexity

• SWA의 Computational cost는 기존의 학습과정과 거의 차이가 나지 않습니다. 학습 중에 weights average를 저장해야 하는데, 일반적으로 DNN의 메모리 사용량은 주로 weight보다 activation func에 영향을 받습니다. 결과적으로 large scale DNN의 경우에도 많아야 10% 정도의 메모리 증가가 발생한다고 합니다.

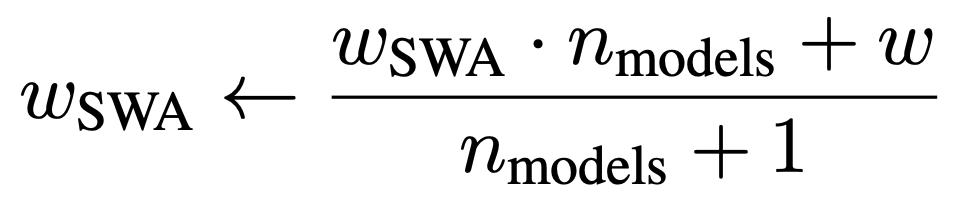
• 시간복잡도도 별로 차이가 없습니다. Updating weight average에 필요한 시간복잡도는 O(1)이며, 기존의 weight와 새로 계산한 weight를 weighted sum하는 연산이므로 연산 자체도 복잡하지 않습니다. 논문에서는 averaging 연산을 epoch당 1회 하였을 때, SGD와 SWA의 computational cost가 동일했다고 합니다.

Solution Width

• 선행연구에서 local optima의 width가 generalization 성능에 영향을 미친다는 것을 보인 바 있습니다. 논문에서는 local optimum의 width가 왜 중요한지에 대해 train loss surface와 test error surface가 서로 영향을 주고받기 때문에 넓은 local optimum을 가진 상태로 수렴하는 것이 바람직하다고 설명합니다.

  직관적으로 이해해 보자면, local optimum width가 넓으면 이에 해당하는 test error surface도 넓을 테니 조금 더 다양한 문제에 대응할 수 있게 된다는 논리입니다.

• 논문에서는 SWA가 SGD보다 wider solution을 제공한다고 합니다. 실험과정은 생략하겠습니다.

Connection to Ensembling

• FGE는 loss space 상에서 서로 가까운 points를 기반으로 ensembling을 진행합니다. 결과적으로 다양한 prediction을 averaging하게 됩니다. 반면에 SWA는 prediction이 아니라 weights를 averaging합니다. 하지만 두 방법은 유사한 결과를 보여준다고 합니다.

  자세한 증명과정에 대해서는 논문을 참고하세요.

Connection to Convex Minimization

• 증명 과정이 상당히 복잡한데, 요점만 정리하면 다음과 같습니다.

1. low train loss를 항상 만족하는 집합들이 존재합니다. (local or global optimum)

2. high constant 또는 cyclical lr로 SGD를 돌리면 이러한 집합들을 지나갈 수 있습니다. (traverse the surface of the sets)

3. SGD의 문제점은 중심으로 진입하지 못하고 주변을 맴돈다는 데 있습니다.

4. SWA는 평균을 구하는 방법으로 center of surface로 진입할 수 있습니다. 즉, SGD보다 더 optimal한 solution을 구할 수 있습니다.

Experiments

• 논문에서는 ImageNet, CIFAR-10 & 100에 대해 SWA와 SGD, FGE를 비교했습니다.

• 전통적인 SGD는 standard decaying learning rate를 사용합니다. 구체적으로는 전체 epochs = $B$일 때, 0.5$B$까지는 고정된 lr ($\alpha_1$)을 사용하였고, 0.5~0.9$B$까지는 0.01$\alpha_1$까지 감소시켰으며, 0.9$B$부터 학습 종료까지는 해당 값을 고정시켜서 학습시켰습니다.

• SGD에서 수렴까지 필요한 epochs $B$ = Budget으로 놓고 성능을 측정한 결과는 다음과 같습니다.

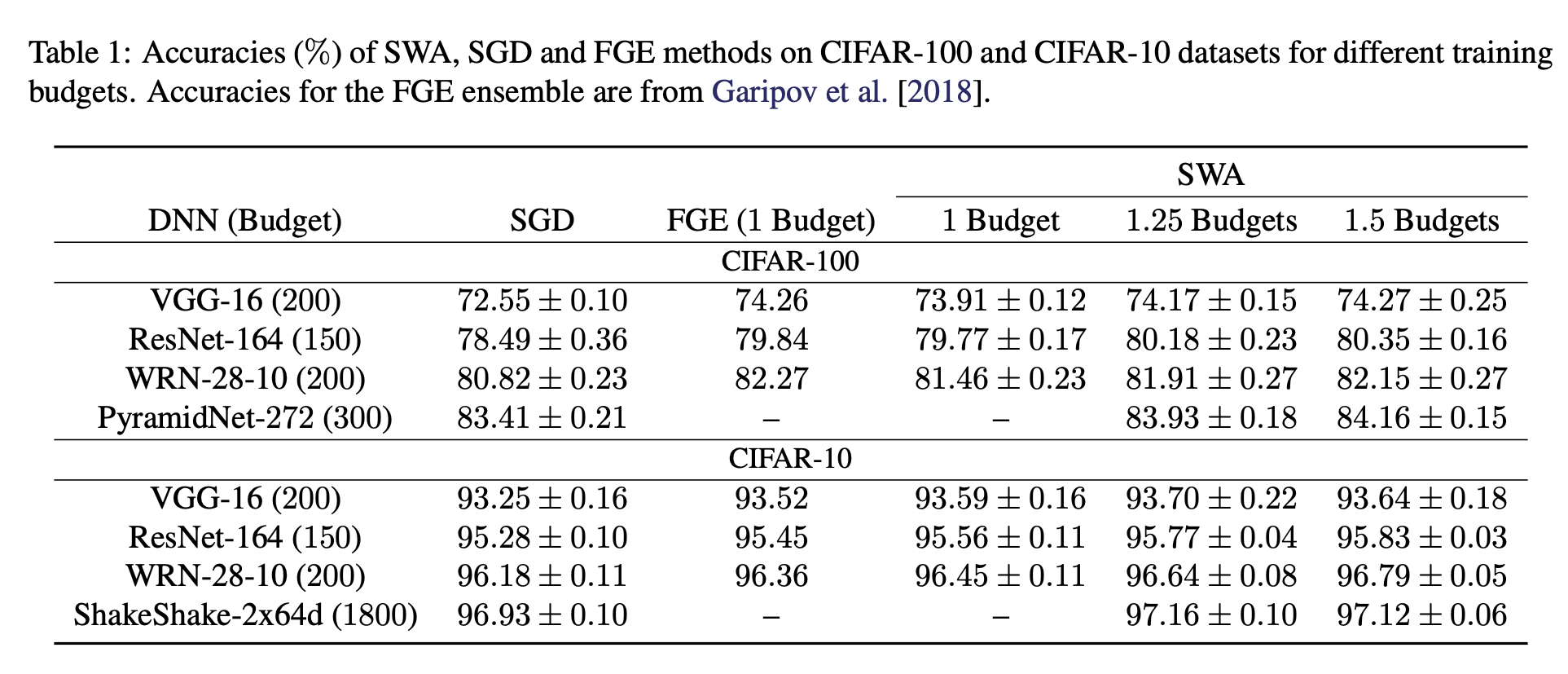
• 실험 결과에 따르면 Budget이 증가할 수록 성능도 같이 증가합니다. SGD는 Budget을 늘려도 더 수렴하지 않기 때문에, SWA가 SGD보다 Flatter Solution을 갖는다고 할 수 있습니다.

• SWA는 FGE와도 동등하거나 그 이상의 성능을 낼 수 있었는데요. 단일 모델 VS 앙상블 모델이라는 점을 고려하면 Computational cost 대비 성능비가 훨씬 훌륭하다고 할 수 있겠습니다.

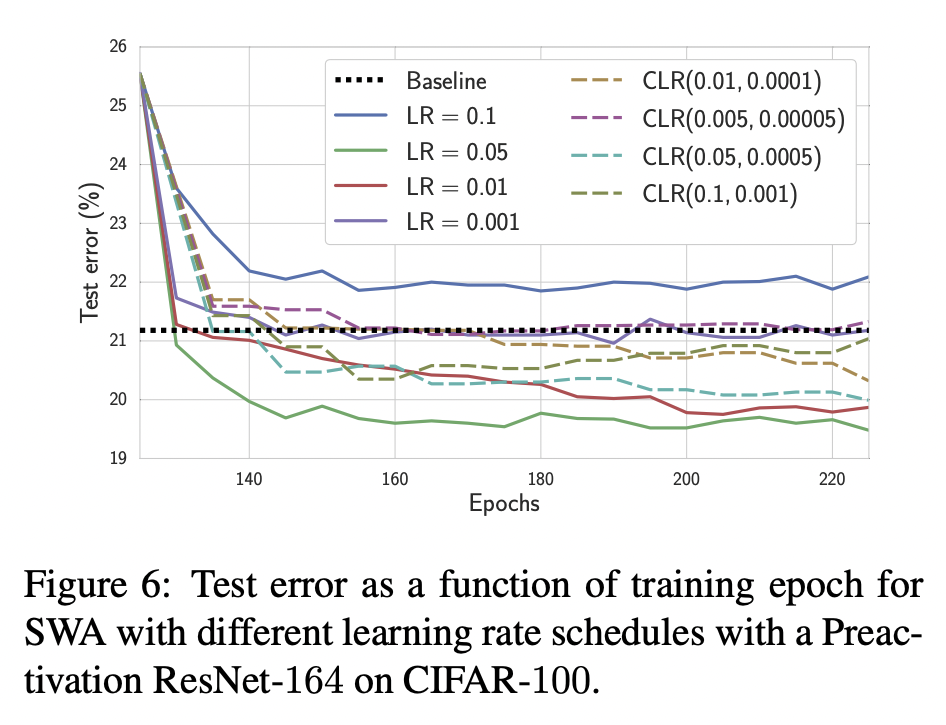
• Constant / Cyclical Learning rate에 따른 실험 결과는 위와 같습니다. LR=0.05, 0.01일 때 성능이 가장 좋은데, 이는 cyclical learning rate를 굳이 사용하지 않아도 됨을 의미합니다.

  그럼 그냥 처음부터 scheduling없이 fixed learning rate를 사용해도 될까요?

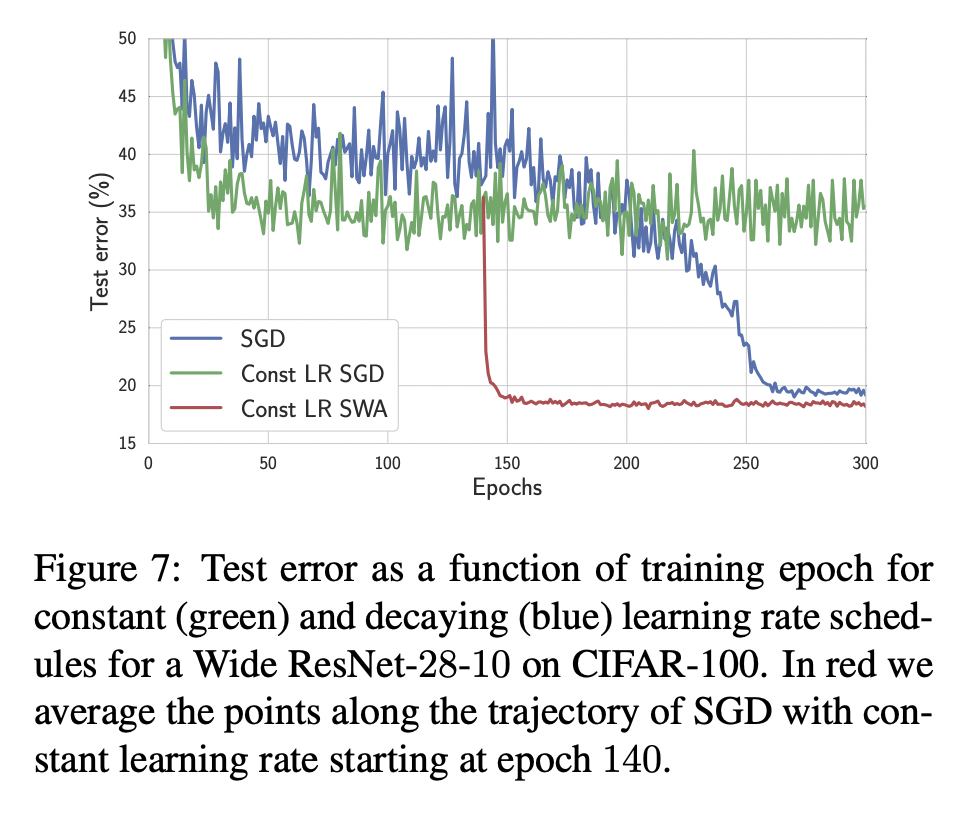
• 위 그림은 이에 대한 실험 결과입니다. 앞서 질문에 대한 답은 "YES"가 되겠네요. 붉은색 실선이 fixed lr을 사용한 SWA의 수렴 그래프인데, Conventional SGD보다 더 빠르고 정확한 수렴을 보여주고 있습니다.

주2:
흥미로운 점은 SGD와 SWA의 수렴이 시작되는 지점이 비슷하다는 것인데요. 이는 수렴이 시작되는 특정 지점, 다시 말해 local optimium surface 근처까지는 SGD를 사용하고, 해당 지점을 지나면서부터 SWA를 사용하면 학습 효율을 증가시킬 수 있다는 것을 의미합니다. 저자들도 이와 같은 학습 방식을 권장합니다.

---

참고문헌

1. HOYA님의 SWA paper review (https://hoya012.github.io/blog/SWA/)
2. Like_Me님의 SWA review (https://simpling.tistory.com/23)