Preprint in ICLR 2017

---

요약

• Factor of Variation (FOV)를 개념적으로 정의하고 이를 찾아내는 새로운 방법을 제안

• VAE에 $\beta$ 계수를 추가하여 representation의 disentangle 강도를 조절할 수 있음

• VAE의 구조적 한계로 인해 reconstruction quality와 disentanglement 간의 trade-off가 존재

---

Background

기본적으로 모든 딥러닝 모델의 목표는 'good representation을 학습하는 것'이라고 할 수 있습니다. 그렇다면 어떤 representation이 good representation일까요?

벤지오의 2013년도 논문에서 힌트를 찾아봅시다.

Good representations are expressive, meaning that a reasonably-sized learned representation can capture a huge number of possible input configurations.

- Y. Bengio (2013)

이 정의에 따르면 good representation이란 적당한 크기 안에서 많은 일을 처리할 수 있도록 다양한 정보를 내포하는 expressive한 특성을 가져야 합니다. 그렇다면 'the best representation'에는 모든 task에 활용할 수 있는 모든 정보가 들어 있을까요?

아쉽게도(?) 그렇지 않습니다.

따라서 현실의 딥러닝은 주어진 데이터를 최대한 이용하여 가능한 task-specific하면서도 동시에 general한 representation을 얻어야 하는 상당히 모순적인 목표를 가지게 됩니다. (bias & variance trade-off)

Factors of Variation (FOV)

Generative model 관점에서 볼 때, task-specific하면서 동시에 general한 representation을 얻기 위한 방법 중 하나는 학습 과정에서 Factor of Variation (FOV)을 고려하는 것입니다.

FOV는 이름 그대로 output의 변화를 조절하는 어떤 가상의 factor들을 의미합니다. 예를 들어 고양이 이미지를 생성한다면 고양이의 표정, 얼굴 모양, 털 색, 줄무늬 모양 등을 관장하는 generative factor들이 있을 것이라 가정하는 거죠. 이런 factor들에 대한 정보를 representation에 학습시킬 수 있다면 이론적으로는 representation만 가지고도 결과물을 조정하는 것이 가능해집니다.

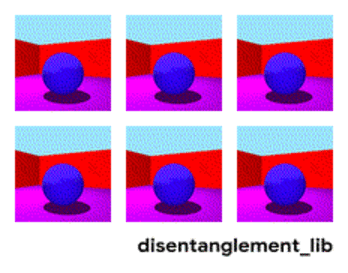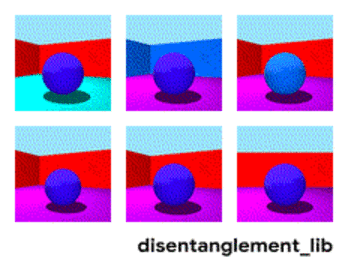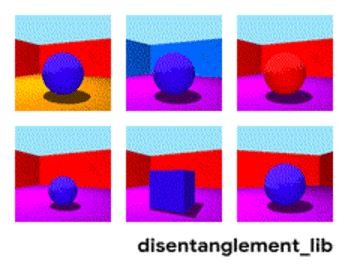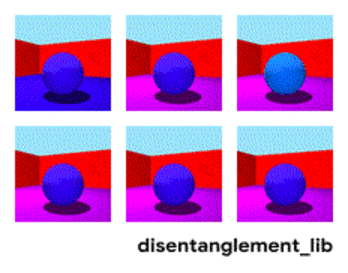
예를 들어 딥마인드에서 배포하는 3dshapes 데이터셋을 보면 공의 색깔, 모양, 크기, 벽과 바닥의 색상, 시점까지 총 6개의 ground truth generative factor를 가지고 있습니다. 각 factor에 해당하는 값을 바꾸면 위 그림처럼 결과물이 변화합니다.

그런데 이렇게 결과물을 직접 조정하는 것은 이미 ground truth factor를 알고 있는 synthetic dataset에서나 가능합니다. 실제 데이터에서는 ground truth factor가 직접적으로 드러나지 않기 때문입니다.

대부분의 딥러닝 모델은 학습 시 FOV를 그다지 신경 쓰지 않습니다. 그 결과 각 factor들이 서로 분리되지 않은 채 학습되는 Entangled Representation 문제가 발생합니다.

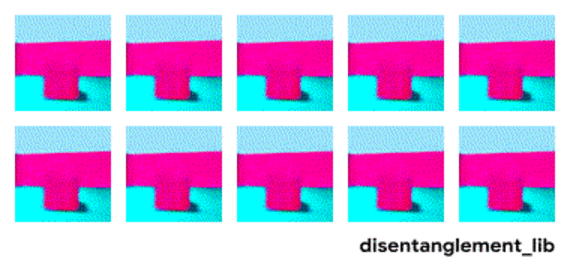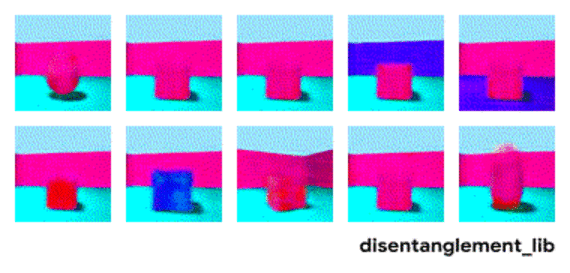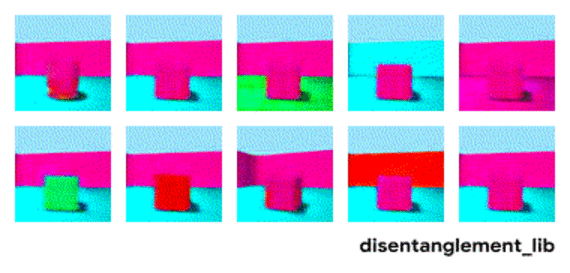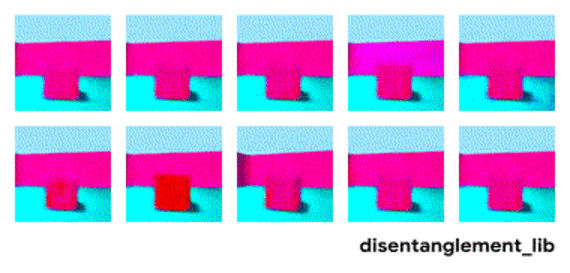
Entangled (latent) representation이 문제가 되는 이유는 위 그림처럼 factor와 output 간의 alignment를 저하시키기 때문입니다.

Classification처럼 모델의 성능을 평가할 때 disentanglement를 고려하지 않아도 되는 task라면 entangled representation을 사용해도 별 문제가 없습니다. 하지만 Text to Image (T2I)처럼 결과물에 대한 controllability가 필요한 task에서는 disentanglement를 고려해야 합니다.

Disentangled Representation Learning (DRL)

따라서 이러한 FOV들을 잘 분리된 상태로 학습하고자 하는 연구들을 Disentangled Representation Learning (DRL)이라고 부릅니다. DRL에는 여러 가지 접근 방식이 있지만 대부분 다음과 같은 두 가지 목표를 공유합니다.

1. 각 factor들이 서로 독립일 것
2. 각 factor가 output의 각 component와 1:1 매칭될 것

결과적으로 representation의 각 unit이 서로 독립이면서 개별 factor를 표현하도록 학습하게 됩니다. 각 unit이 각각의 generative factor에 1:1로 매칭되기 때문에 높은 interpretatbility도 얻을 수 있습니다.

통계적 독립은 의미적 독립을 보장하지 않습니다. 즉, 각 unit이 서로 간에 fully independent하더라도 개별 unit에 할당되는 generative factor가 서로 독립이라는 보장은 없습니다.

최근에는 이 점에 착안해 인과추론을 이용하는 연구도 많이 진행되고 있습니다.

VAE and $\beta$-VAE

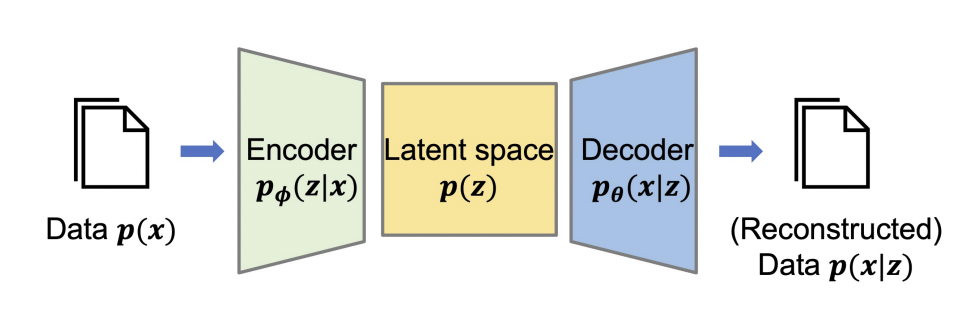
본 논문에서 제안하는 $\beta$-VAE는 쉽게 말해 disentanglement를 고려한 VAE입니다. 모델 구조도 VAE와 동일하며 objective function도 매우 유사합니다.

VAE의 궁극적인 목표는 디코더를 잘 학습시키는 것입니다. 즉, 위 그림에서 $p_\theta(x|z)$를 잘 학습시켜서 좋은 $\theta$를 얻고자 합니다.

그런데 latent space의 분포 $p(z)$에 대한 정보가 없으므로 가우시안을 가정합니다.

그리고 임의의 함수를 만들어서 $p(z)$를 근사시킵니다. 이게 인코더입니다.

식 (1)과 식 (3)이 같아지도록 만듭니다.

결과적으로 VAE의 objective function은 다음과 같이 나타낼 수 있습니다.

여기까지 보면 VAE는 disentanglement를 고려하지 않는다는 것을 알 수 있습니다.

Assumptions

그래서 저자들은 disentanglement를 학습시키기 위해 2가지 가정을 세웁니다.

1. conditional independent factor $v\in V$가 존재한다.
2. conditional dependent factor $w\in W$가 존재한다.

여기서 $V,W$는 모두 generative factor들의 집합입니다. 또, conditional independent하다는 것은 엄밀한 수학적 정의가 아니라 오히려 추상적인 개념에 가깝습니다. 예를 들어 고양이 이미지를 생성하는 conditional independent factor는 '네 다리가 달려 있을 것', '수염이 달려 있을 것', '복슬복슬한 털이 있을 것' 등이고, '각각의 다리에는 육구가 있을 것', '수염의 개수는 12쌍 24개일 것', '털의 색은 노란색에 주황색의 줄무늬가 있을 것' 등이 conditional dependent factor에 해당합니다.

아무튼, 이러한 $V,W$가 존재한다고 가정하고 이들의 분포 $p(v, w)$를 학습하면 data를 만들어내는 simulator를 모방할 수 있을 것이라는 게 저자들의 생각입니다.

개인적으로 이를 학습하기 위한 방법을 유도하는 과정이 궁금했는데 아쉽게도 본 논문에는 잘 설명돼 있지 않습니다. 대신 왜 이 방법이 잘 작동하는가에 대한 후속 연구가 많으니 궁금하면 찾아 읽어보길 권합니다.

$\beta$ regularization

저자들은 $V,W$를 학습시키기 위해 VAE에 추가적인 regularization term을 추가합니다. 구체적인 방법은 다음과 같습니다.

VAE에서 (3)까지의 과정은 동일하게 진행하되 KLD를 감소시킬 때 최종 KLD 값이 임의의 capacity $\epsilon$보다 작도록 강제합니다.

여기에 라그랑주 승수법을 이용하면 다음과 같은 objective function을 얻습니다.

식 (7)이 $\beta$-VAE의 최종적인 목적함수가 됩니다.

Understanding dynamics of $\beta$

단순히 $\beta$ 계수를 추가한 것 만으로 $V,W$를 학습할 수 있다는 게 흥미로운데, 후속 논문에 따르면 이는 information bottleneck과 밀접한 연관이 있습니다.

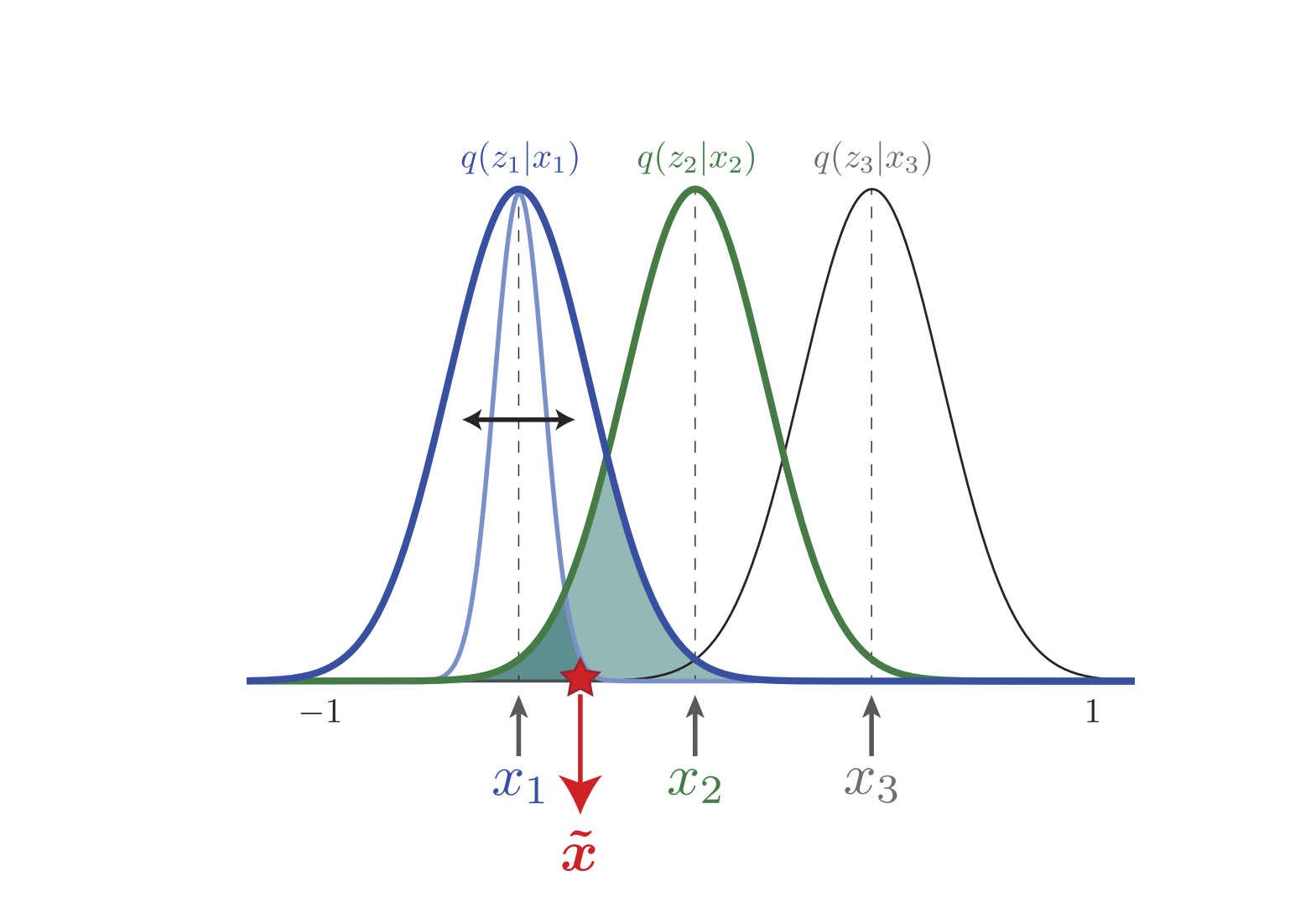
$\beta$는 정보 채널 간의 mixing coefficient로 볼 수 있습니다. 여기서 정보 채널이란 구체적으로 분포를 근사하기 위해 사용되는 각 가우시안을 가리킵니다. 예를 들어 위 그림에서 $q(z_1|x_1), q(z_2|x_2),q(z_3|x_3)$ 등은 모두 정보 채널입니다.

실험에 따르면 $\beta>1$이어야 disentangling이 잘 된다고 하는데, KLD 항의 영향력을 강화하여 information bottleneck을 더 좁게 만들어야 효율적인 학습이 가능하다는 의미로 이해할 수 있습니다. ($\beta=1$이면 오리지널 VAE가 됩니다.)

그런데 $\beta$값이 커지면 posterior가 prior gaussian $N(0,I)$를 따르려고 하는 과정에서 각각의 가우시안 채널이 겹쳐지므로 데이터를 통해 얻을 수 있는 정보가 중첩됩니다. 즉, 데이터를 통해 얻을 수 있는 유의미한 정보가 줄어듭니다. 결과적으로 각 데이터의 차이를 구분하는 능력(model capacity)이 저하되어 reconstruction error가 증가하게 됩니다. 예를 들어 위 그림을 보면 실제로는 $\tilde{x}$가 $q(z_2|x_2)$에서 샘플링되었음에도 불구하고 $q(z_1|x_1)$에 대한 likelihood가 더 높습니다.

이런 상황에서 reconstruction error를 줄이려면 서로 비슷한 데이터를 가깝게 모아야 합니다. 다시 말해 각 gaussian이 비슷한 데이터의 분포를 근사할 수 있도록 각 데이터의 고유한 특징을 잘 학습해야 합니다. 이 경우에는 conditional (in)dependent factor $v,w$를 잘 찾아내야 하겠죠?

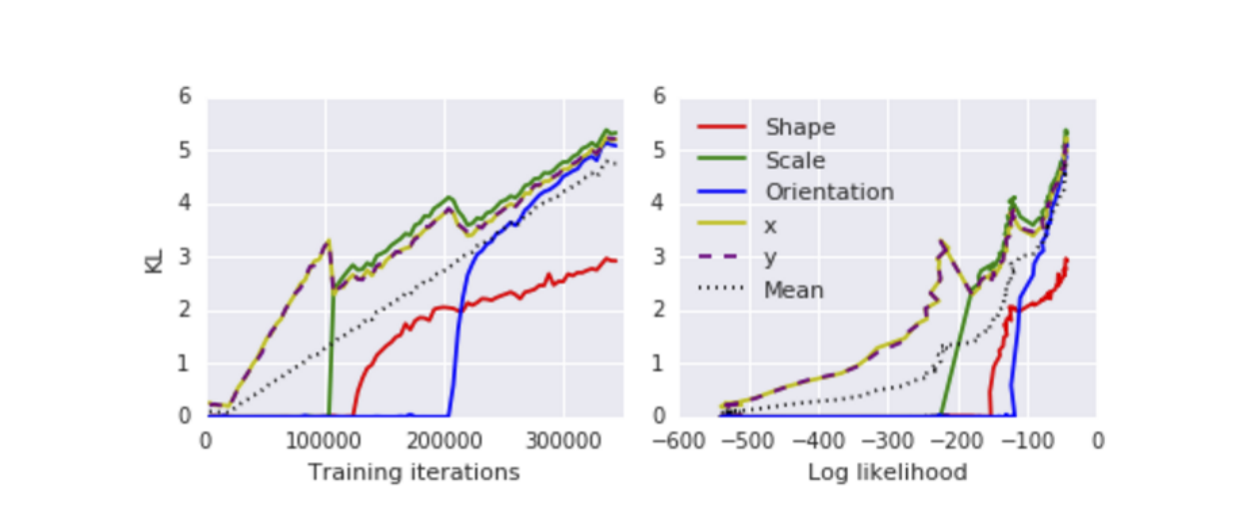
실제로 $\beta$-VAE의 prior distribution을 모사한 모델로 실험한 결과, 위와 같이 중요한 factor부터 모델링(학습)되는 것을 확인할 수 있습니다. 이 실험에서는 $x,y$ 좌표가 conditional independent factor $v$에 해당한다고 볼 수 있습니다.

지금까지의 흐름을 보면 예상할 수 있겠지만 $\beta$-VAE는 reconstruction quality와 disentanglement 간에 trade-off를 가지고 있습니다.

다만 이건 논문에서 제안하는 regularization 방식의 문제라기보다는 VAE의 information bottleneck 구조에서 기인하는 근본적인 한계라고 봐야 합니다. 실제로 diffusion 계통의 T2I (Text to Image) 모델에서는 $\beta$-VAE만큼 극명한 trade off가 발생하지 않습니다.

Evaluation of disentanglement

자, 그렇다면 $\beta$의 영향력을 어떻게 평가할 수 있을까요?

앞서 언급했듯이 $\beta$값이 너무 커지면 posterior collapse가 발생합니다. 따라서 데이터에 따라 적절한 $\beta$값을 정하는 게 중요한데, $\beta$값이 바뀌면 likelihood 값도 변하기 때문에 단순히 log likelihood를 기준으로 disentanglement를 판단하는 것은 타당하지 않습니다.

따라서 저자들은 새로운 disentanglement 측정 방식을 제안하였습니다.

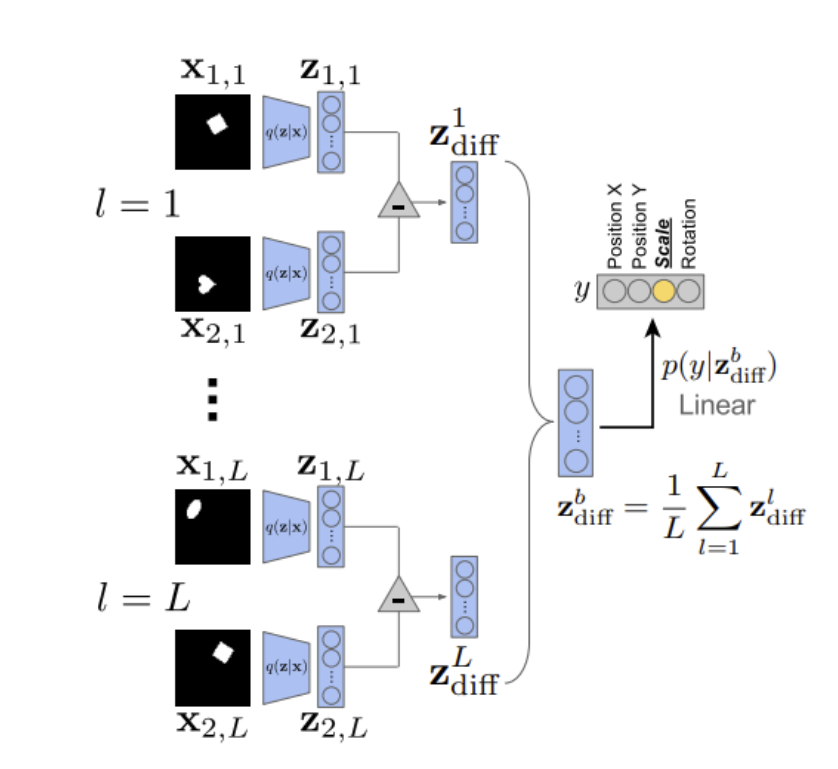
구체적인 방법은 다음과 같습니다.

먼저 학습된 representation에서 임의의 한 unit을 제외한 나머지 값을 고정합니다. 그리고 이를 바꿔가며 linear classification 성능을 평가하면 해당 factor의 disentanglement가 성능에 미치는 영향을 알 수 있습니다.

만약 disentangle이 잘 되었다면 classfication에 필요한 각 이미지의 특징이 잘 포함돼 있을 테니 오차율이 낮을 것이고, disentangle이 잘 되지 않았다면 그 반대가 되겠죠.

물론 이 방법은 class label이 필요하다는 단점이 있습니다. 이미지 데이터는 보통 레이블이 없기 때문에 다른 평가 방법[1][2]들을 사용하기도 합니다.

Overall...

$\beta$-VAE는 2024년 현재 기준으로는 꽤 오래된 논문이기 때문에, 개념을 정의하거나 가정을 세우는 방식이 다소 원시적이고 저자들의 직관에 의존하는 경향이 있습니다. 하지만 여전히 DRL 분야에서는 대표적인 베이스라인으로 사용되며 $\beta$-VAE에서 파생된 연구 흐름도 존재하기 때문에 충분히 읽어둘 가치가 있습니다.