[딥러닝] VICReg: Variance-Invariance-Covariance Regularization for Self-Supervised Learning

Ethan·2024년 1월 28일

DL VICReg ssl

Papers Review

목록 보기

17/18

Published in ICLR 2022

요약

Siamese network 구조에서 representation collapse를 방지하기 위한 명시적인 objective function 제시
- Variance, Invariance, Covariance regularization term
Momentum encoder, memory bank 등의 테크닉 대신 사용가능한 모듈화 기법 제안

Background

최근 Image Representation learning 분야에서는 BYOL (Grill et al, 2020)과 SimSiam (Chen & He, 2021)을 필두로 동일한 이미지에 다른 augmentation을 적용하여 뽑아낸 embedding들을 가지고 학습을 진행하는 연구가 많이 발표되었습니다.

헌데 이런 식의 pairwise learning을 진행하다보면 인코더가 constant 또는 non-informative vectors를 생성하게 되는 (representation) collapse 문제가 발생합니다. 아직 collapse가 발생하는 근본적인 원인이 명확하게 밝혀져 있지 않기 때문에 이에 대해 Batch Normalization이나 Stop gradient, Memory bank나 Predictor head를 추가하는 등 여러 해결 방안이 제시되었습니다.

예를 들어 Siamese Network들은 주로 contrastive learning과 infoNCE loss를 사용하는데 그 특성상 필연적으로 많은 contrastive pair dataset을 요구합니다. 반대로 개별 데이터를 보지 않고 전체 데이터를 clustering 관점에서 접근하는 방법도 있습니다. 예를 들어 DeepCluster (Caron et al, 2018) 같은 방법론은 이전 step에서 얻은 representation에 k-means clustering을 하여 pseudo label을 만들고, 이를 이용하여 새로운 representation을 생성합니다. 이 과정에서 asynchronously clustering phase 자체가 꽤나 큰 computational cost를 요구하기 때문에 pairwise comparison을 하지 않는 SwAV (Caron et al, 2020) 같은 방법도 나왔지만 여전히 negative sample이 많이 필요하다는 단점이 있습니다.

Motivation

Contrastive learning에서 자주 사용하는 InfoNCE loss를 수식으로 표현하면 다음과 같습니다.

L=-\mathbb{E}_X\left[\log \frac{f_k(x_{t+k}, c_t)}{\sum_{x_j\in X}f_k(x_j, c_t)}\right]

위 식에서 $c_t$ 는 과거의 데이터들을 기반으로 연산한 context vector, 다시 말해 현재 time step에서의 latent representation입니다. 이 때 $f(\cdot)$ 은 다음과 같이 context vector와 예측하려는 time step의 latent representation 간의 mutual information density ratio에 비례하는 autoregressive model입니다.

f(x_{t+k}, c_t)\propto I(x_{t+k},c_t)=\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}

Expectation 항은 모델의 예측값인데 loss를 최소화하려면 로그항의 분자가 커져야 하고, $I(x_{t+k},c_t)$ 의 lower bound는 다음과 같으므로

I(x_{t+k},c_t)\geq\log N-L_N^{opt}

sample의 개수 $N$ 이 커질 수록 lower bound 값이 높아져서 더 많은 정보량을 얻어낼 수 있습니다. 즉, 주어진 sample이 많을수록 실제 분포를 더 잘 근사할 수 있지만 autoregressive model $f$ 가 batch size에 민감해지는 trade-off가 발생합니다. 만약 배치 사이즈를 줄일 수 없다면 모델을 잘 설계하는 수밖에 없는데, 수식을 보면 어떤 $f$ 가 '좋은' 모델인지에 대한 조건이나 힌트가 따로 주어지지 않습니다.

그래서 Barlow Twins (Zbontar et al, 2021)나 W-MSE (Ermolov et al, 2021) 같은 연구에서는 Information Maximization 관점으로 접근합니다. Representation collapse는 embedding vector가 내포하는 정보량을 감소시키기 때문에 문제가 되는 것이므로 반대로 정보량을 극대화하는 방법을 찾아보자는 것입니다.

VICReg도 information maximization 관점에서 representation collapse 방지를 위한 explicit objective function을 제안하고, weight sharing이나 stop gradient, memory bank 등 implicit한 representation collapse 방지 테크닉을 사용하지 않아도 된다는 점을 보여줍니다.

Model Architecture

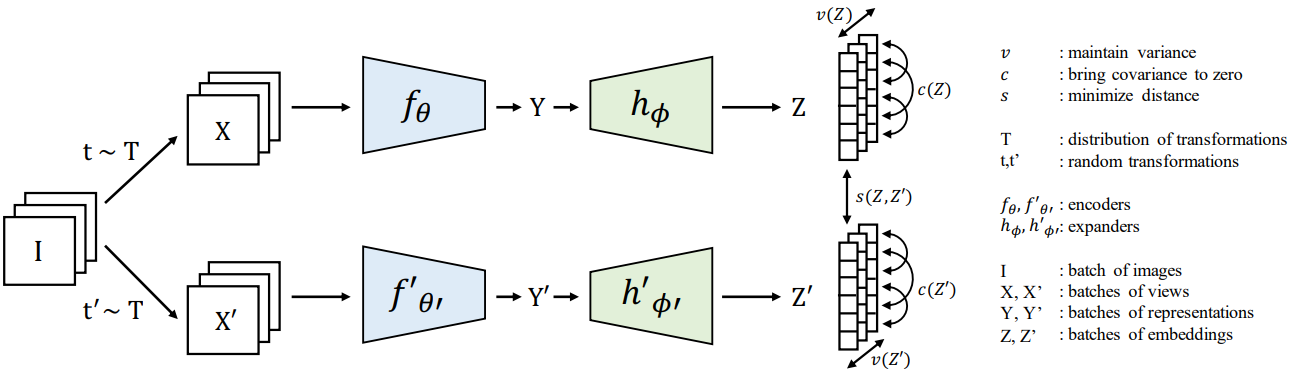
VICReg의 전체 구조는 위 그림과 같습니다. 참고로 VICReg 자체는 꼭 Siamese network가 아니어도 사용가능합니다.

Encoder $f_\theta$ 는 downstream task에 사용할 representation을 생성하고, expander $h_\phi$ 는 생성된 representation을 embedding space로 mapping합니다. 이 때 expander는 두 representation에서 서로 다른 부분을 제거하고, 임베딩 벡터의 차원을 non-linear하게 확장하여 representation vector 내부 변수들의 상관성을 최대한 감소시킵니다. 설명이 복잡해 보이지만 구조 자체는 BYOL이나 SimSiam과 같은 단순한 MLP block입니다.

parser.add_argument("--arch", type=str, default="resnet50",
                        help='Architecture of the backbone encoder network')
                        
parser.add_argument("--mlp", default="8192-8192-8192",
                        help='Size and number of layers of the MLP expander head')
                        
def Projector(args, embedding):
    mlp_spec = f"{embedding}-{args.mlp}"
    layers = []
    f = list(map(int, mlp_spec.split("-")))
    for i in range(len(f) - 2):
        layers.append(nn.Linear(f[i], f[i + 1]))
        layers.append(nn.BatchNorm1d(f[i + 1]))
        layers.append(nn.ReLU(True))
    layers.append(nn.Linear(f[-2], f[-1], bias=False))
    return nn.Sequential(*layers)

Official code를 보면 Linear - BatchNorm - ReLU 순으로 구성돼 있습니다. 학습이 완료된 후에는 encoder가 생성한 representation $Y$ 만 사용합니다.

Loss function

VICReg의 loss function은 다음과 같이 3개의 sub-objective terms로 구성돼 있습니다.

\begin{aligned} L&=\sum_{I\in D}\sum_{t, t'\sim \mathcal{T}}l(Z^I, Z'^I)\\ \\ &=\lambda s(Z, Z')+\mu[v(Z)+v(Z')]+\nu[c(Z)+c(Z')] \end{aligned}

$I$ 는 image batch이고 $Z,Z'$ 는 생성된 representation batch입니다. $\lambda, \mu, \nu$ 는 모두 하이퍼파라미터인데 $\nu=1$ 이고 $\lambda=\mu>1$ 로 놓았을 때 가장 성능이 좋았다고 합니다.

1) Invariance $s(\cdot)$

s(Z,Z')=\frac{1}{n}\sum_i\lVert z_i-z'_i\rVert_2^2

두 augmented image 간의 MSE를 줄여서 유사한 부분만 추출합니다. 학습이 진행되면서 두 임베딩 벡터의 공통점을 제외한 나머지 불필요한 정보들을 제거하는 역할입니다. 어차피 동일한 이미지에서 추출한 임베딩 벡터이므로 굳이 normalization을 하지 않아도 됩니다.

2) Variance $v(\cdot)$

\begin{aligned} v(Z)&=\frac{1}{d}\sum_{j=1}^d\max\left(0,\gamma-S(z^j,\epsilon)\right)\\ \\ &=\frac{1}{d}\sum_{j=1}^d\max\left(0,\gamma-\sqrt{\text{Var}(z^j)+\epsilon}\right) \end{aligned}

여기서 말하는 variance는 임베딩 벡터 내 각 feature들의 분산입니다. $z^j$ 는 임베딩 벡터 $z$ 의 $j$ 번째 차원(feature)에 위치한 값이고 $\gamma$ 는 constant target value입니다.

Contrastive loss와 유사한 형태인데 margin과 euclidean distance 대신 target value와 std를 사용합니다. 학습이 진행되면서 임베딩 벡터 간의 invariant가 감소하여 분산이 줄어들면 편차가 $\gamma$ 로 수렴하고, 결과적으로 일정 수준 이상의 표준편차를 보장하게 되어 representation collapse를 방지할 수 있습니다. 논문에서는 $\gamma=1$ 로 설정하였습니다.

만약 표준편차 대신 분산 $\text{Var}(x)$ 를 사용한다면 $S(\cdot)$ 의 gradient가 0으로 수렴하면서 representation collapse가 발생한다고 합니다. 표준편차를 사용하든 분산을 사용하든 feature variance의 lower bound가 $\gamma$ 로 수렴하는 건 동일할텐데 왜 분산을 사용할 경우에만 representation collapse가 나타나는지는 의문이네요. 어쩌면 variance term이 collapse를 완벽하게 방지하지 못하고, 오히려 천천히 collapsing이 발생하는 중일 수도 있겠습니다.

3) Covariance $c(\cdot)$

\begin{aligned} c(Z)&=\frac{1}{d}\sum_{i\neq j}[C(Z)]^2_{i,j}\\ \\ &=\frac{1}{d}\sum_{i\neq j}\left[\frac{1}{n-1}\sum_{i=1}^n(z_i-\bar{z})(z_i-\bar{z})^T\right]^2_{i,j},\quad \text{where}\quad\bar{z}=\frac{1}{n}\sum_{i=1}^nz_i \end{aligned}

수식을 최적화하면 covariance matrix $C(Z)$ 의 비대각원소(off-diagonal coefficients)들이 0으로 수렴하여 피처끼리 decorrelate됩니다. 결과적으로 각 차원의 피처 벡터들이 상대적으로 독립인 정보를 인코딩하게 되므로 전체 임베딩 벡터의 관점에서는 유의미한 정보량이 증가합니다.

물론 공분산이 0이라도 비선형적으로는 독립이 아닐 수 있지만 일반적으로 non-linear한 neural net에서 다중공선성이 큰 문제가 되지는 않습니다. 최근에는 처음부터 매우 많은 데이터를 가지고 모델을 학습시키기 때문에 다중공선성을 가질 확률 자체가 낮아지기 때문입니다. Prediction 등의 task에서 성능을 따질 때는 인과와 상관을 크게 구분하지 않기도 하고요.

Experiment Results

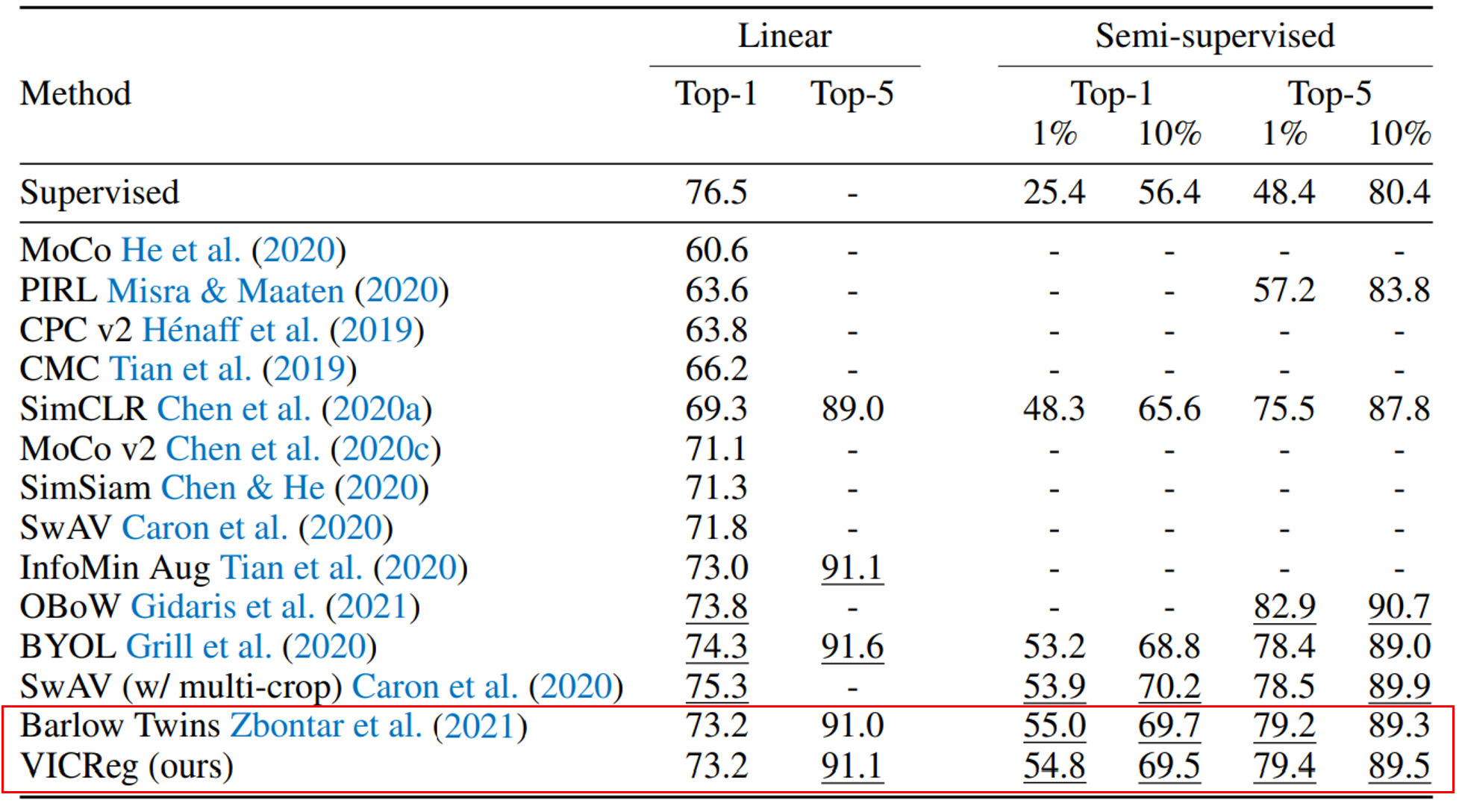
VICReg의 openreview를 보면 Barlow Twins와 뭐가 다른지 잘 모르겠다는 리뷰가 많은데 실제로 성능은 거의 차이가 없습니다. 대신 explicit variance term이 추가되었고 objective function이 모듈화되었기 때문에 개별 branch에 쉽게 적용할 수 있다는 장점이 있습니다.

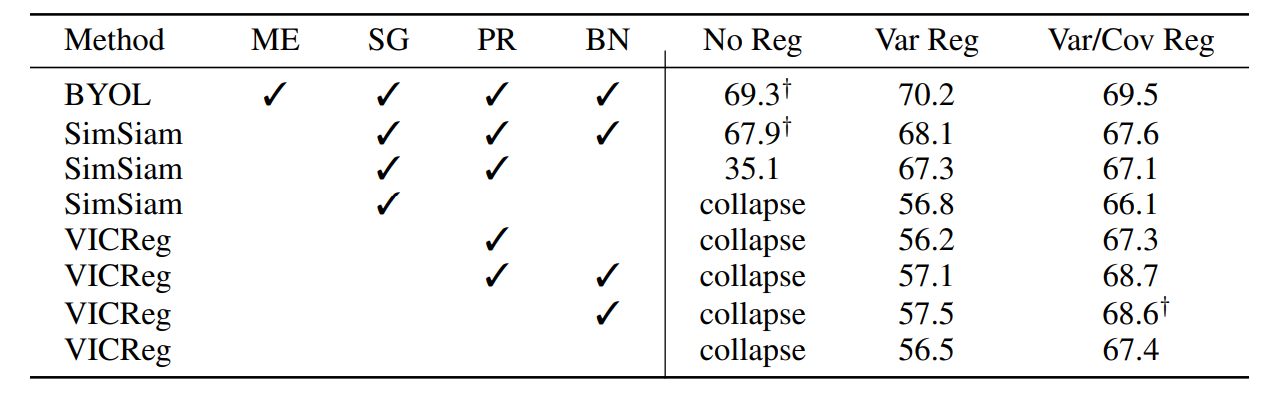
ME는 momentum encoder, SG는 stop gradient, PR은 predictor, BN은 batch normalization입니다. 표를 보면 모든 method를 사용한 BYOL의 성능이 가장 좋지만 SG와 PR만 사용하였을 때에도 comparable한 결과를 얻을 수 있습니다.

PR과 SG 둘 중 하나라도 없다면 곧바로 representation collapse가 발생합니다. 주목할 점은 BYOL과 SimSiam 모두 variance term을 추가하였을 때 성능이 향상되었는데, 저자들에 따르면 이는 BYOL과 SimSiam이 variance를 잘 보존하지 못하고 있으며, 오히려 매우 천천히 informational collapse가 발생하는 중이라는 증거라고 합니다.

Overall...

VICReg은 representation collapse를 방지하기 위한 explicit하고 모듈화된 방법을 제시했지만 Barlow Twins에 비해 성능이 거의 개선되지 않았다는 단점이 있습니다. 비슷한 성능이라면 VICReg을 사용하는 것이 더 타당하겠지만, siamese network 구조를 전제한다는 점에서 다른 아키텍처에도 쉽게 적용할 수 있을지는 잘 모르겠네요.

Experiment 측면에서도 Covariance regularization term만 사용한 실험 결과가 따로 없다는 것은 다소 아쉽습니다. 특히 본문에서 직접적으로 informational collapse를 방지하기 위한 term이라고 명시했음에도 불구하고, 해당 term만 사용했을 때 collapse가 일어나는지 여부를 보여주지 않은 것은 weak point라고 생각합니다.

Ethan

재미있게 살고 싶은 대학원생

이전 포스트

[신경과학] Serotonin neurons modulate learning rate through uncertainty

다음 포스트