[딥러닝] 어텐션 Attention 2

Ethan·2022년 6월 12일

AI Attention DL 어텐션

인공지능 기초 (feat. AIFFEL)

목록 보기

47/48

전편에서 이어지는 내용입니다.

양방향 RNN (LSTM)

기본 구조의 seq2seq은 인코더가 단방향으로 데이터를 읽습니다. 따라서 특정 시점 $t$ 의 은닉 상태 벡터는 해당 시점 이후의 데이터를 반영하지 못한다는 문제가 있습니다.

이를 해결하기 위해 양방향 RNN 구조를 사용할 수 있습니다.

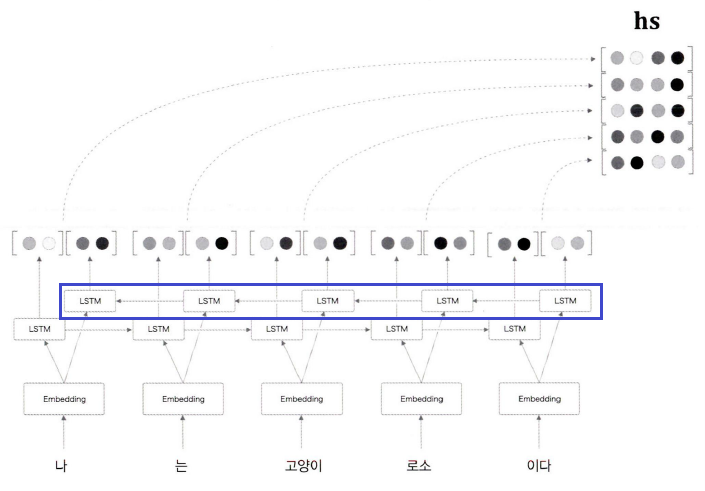
양방향 LSTM의 아이디어는 단순합니다. 바로 2개의 단방향 LSTM 계층을 서로 반대 방향으로 배치하는 것입니다.

위 그림에서 파란색 네모로 표시된 부분이 역방향 LSTM 계층입니다. 해당 구조에서는 두 은닉 상태를 연결시킨 벡터를 최종 은닉 상태 벡터로 사용하지만, 단순히 연결하는 것 외에 합하거나 평균내는 방법도 사용할 수 있습니다.

양방향 RNN의 시퀀스 처리

ABCD 라는 시퀀스를 입력받는다고 가정합니다.
정방향(좌->우) LSTM 계층은 A-B-C-D 순으로 데이터를 처리합니다.
역방향(우->좌) LSTM 계층은 D-C-B-A 순으로 데이터를 처리합니다.

데이터의 입력 순서가 다를 뿐, 두 계층은 동일한 메커니즘의 순전파 연산을 수행합니다.
역전파 연산도 같은 원리로 수행합니다. 코드로 나타내면 다음과 같습니다.

class TimeBiLSTM:
    def __init__(self, Wx1, Wh1, b1,
                 Wx2, Wh2, b2, stateful=False):
        self.forward_lstm = TimeLSTM(Wx1, Wh1, b1, stateful)
        self.backward_lstm = TimeLSTM(Wx2, Wh2, b2, stateful)
        self.params = self.forward_lstm.params + self.backward_lstm.params
        self.grads = self.forward_lstm.grads + self.backward_lstm.grads

    def forward(self, xs):
        o1 = self.forward_lstm.forward(xs)
        o2 = self.backward_lstm.forward(xs[:, ::-1])
        o2 = o2[:, ::-1]
        
		# 두 output을 병합
        out = np.concatenate((o1, o2), axis=2)
        return out

    def backward(self, dhs):
        H = dhs.shape[2] // 2
        do1 = dhs[:, :, :H]
        do2 = dhs[:, :, H:]

		# 역전파 시에는 do1, do2로 나눠서 진행
        dxs1 = self.forward_lstm.backward(do1)
        do2 = do2[:, ::-1]
        dxs2 = self.backward_lstm.backward(do2)
        dxs2 = dxs2[:, ::-1]
        dxs = dxs1 + dxs2
        return dxs

어텐션 계층 사용하기

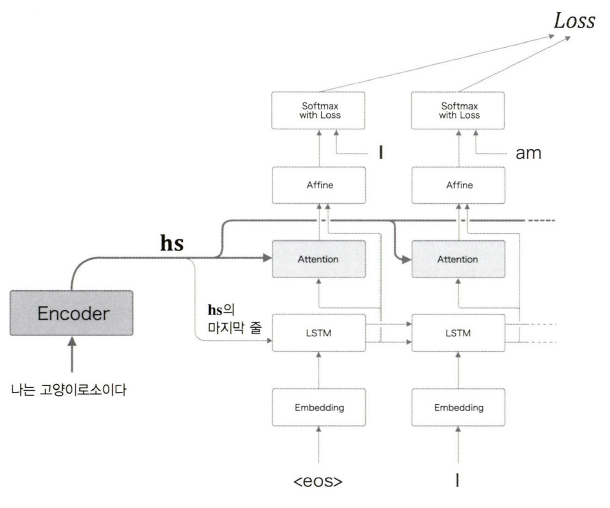
지금까지의 내용에서는 위와 같이 LSTM와 Affine 계층 사이에 어텐션 계층을 도입해 사용했습니다. 하지만 반드시 해당 위치에 어텐션 계층을 삽입할 필요는 없습니다.

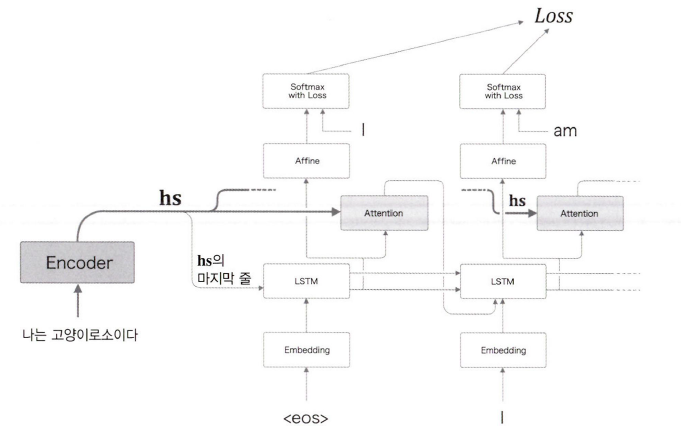
위 그림과 같이 두 노드 사이에 삽입할 수도 있습니다.
이 경우에는 어텐션 계층에서 출력한 맥락 벡터가 다음 LSTM 계층의 입력값이 됩니다.

Note

어텐션 계층의 위치에 따라 최종 정확도가 바뀌는지는 직접 실험하기 전까지 알 수 없습니다.

seq2seq 심층화

현실의 문제는 예제로 다루는 것들보다 훨씬 복잡합니다. 그래서 설명력이 더 높은 네트워크가 필요합니다. 일반적으로 신경망을 깊게 쌓을수록 설명력이 향상되는데, 이는 seq2seq 또한 마찬가지입니다.

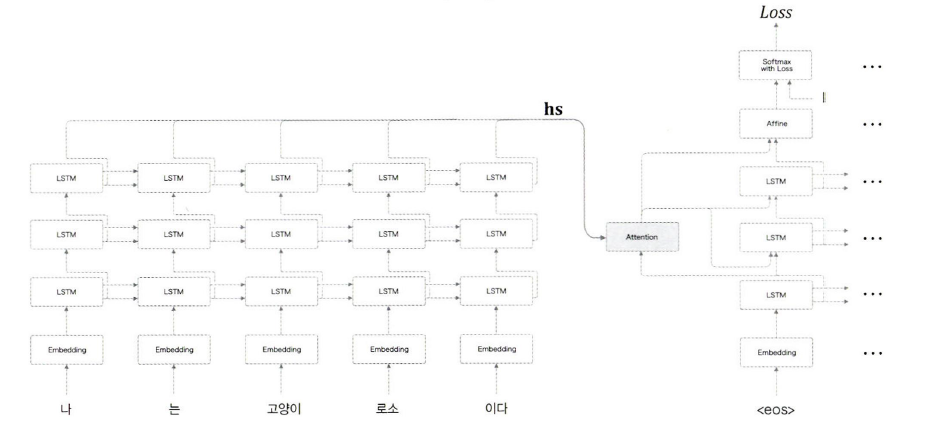
위 그림은 앞서 살펴본 seq2seq 모델에 2개의 LSTM 계층을 추가한 네트워크입니다.

일반적으로 인코더와 디코더의 네트워크 깊이는 동일하게 설계하는 것이 좋습니다. 두 네트워크의 깊이가 다르면 전달되는 맥락 벡터가 변형될 우려가 있기 때문입니다.

위 구조에서는 인코더에서 3중 LSTM 계층을 통해 출력한 $hs$ 행렬 벡터를 어텐션 계층에 전달합니다. 어텐션 계층에서 출력한 맥락 벡터는 다시 디코더의 각 LSTM 계층과 Affine 계층에 전파됩니다.

어텐션 계층의 위치는 네트워크 설계에 따라 달라질 수 있습니다. 중요한 것은 네트워크 깊이가 깊어지더라도 일반화 성능을 유지하도록 하는 것입니다. 이를 위해 일부 노드를 제외시키는 드롭아웃이나, 하나의 계층 내에서라면 시점에 상관없이 가중치가 유지되는 가중치 공유 등의 테크닉을 사용할 수 있습니다.

skip 연결

skip 연결은 계층을 건너뛰는 연결 방식을 말합니다.
잔차 연결(residual connection), short-cut이라고도 합니다.

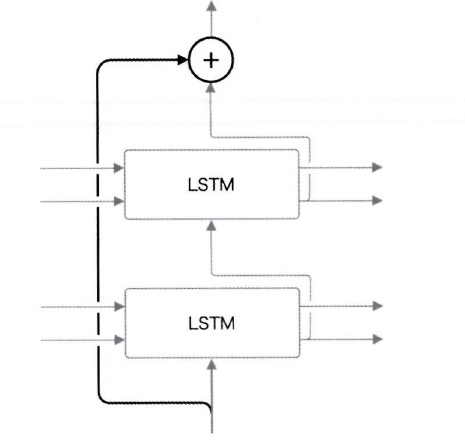
위 그림을 보면 이전 계층의 출력이 두 개의 계층을 건너뛰어 전달되는 것을 볼 수 있습니다.

$\bigoplus$ 부분이 바로 skip 연결의 접속부입니다.
접속부에서는 두 개의 출력끼리 더해집니다. (원소별 덧셈)

이를 통해 기울기 소실/폭발 문제를 예방할 수 있습니다.

어텐션 응용

지금까지는 seq2seq에 한정해 어텐션을 활용했습니다.
아래에서 조금 더 다양한 활용 방법을 소개합니다.

구글 신경망 기계 번역 (GNMT)

Google's Neural Machine Translation System | 논문 링크

신경망 기계 번역(Neural Machine Tanslation)은 번역 과정에서 심층 신경망(DNN)을 사용하는 기법입니다.

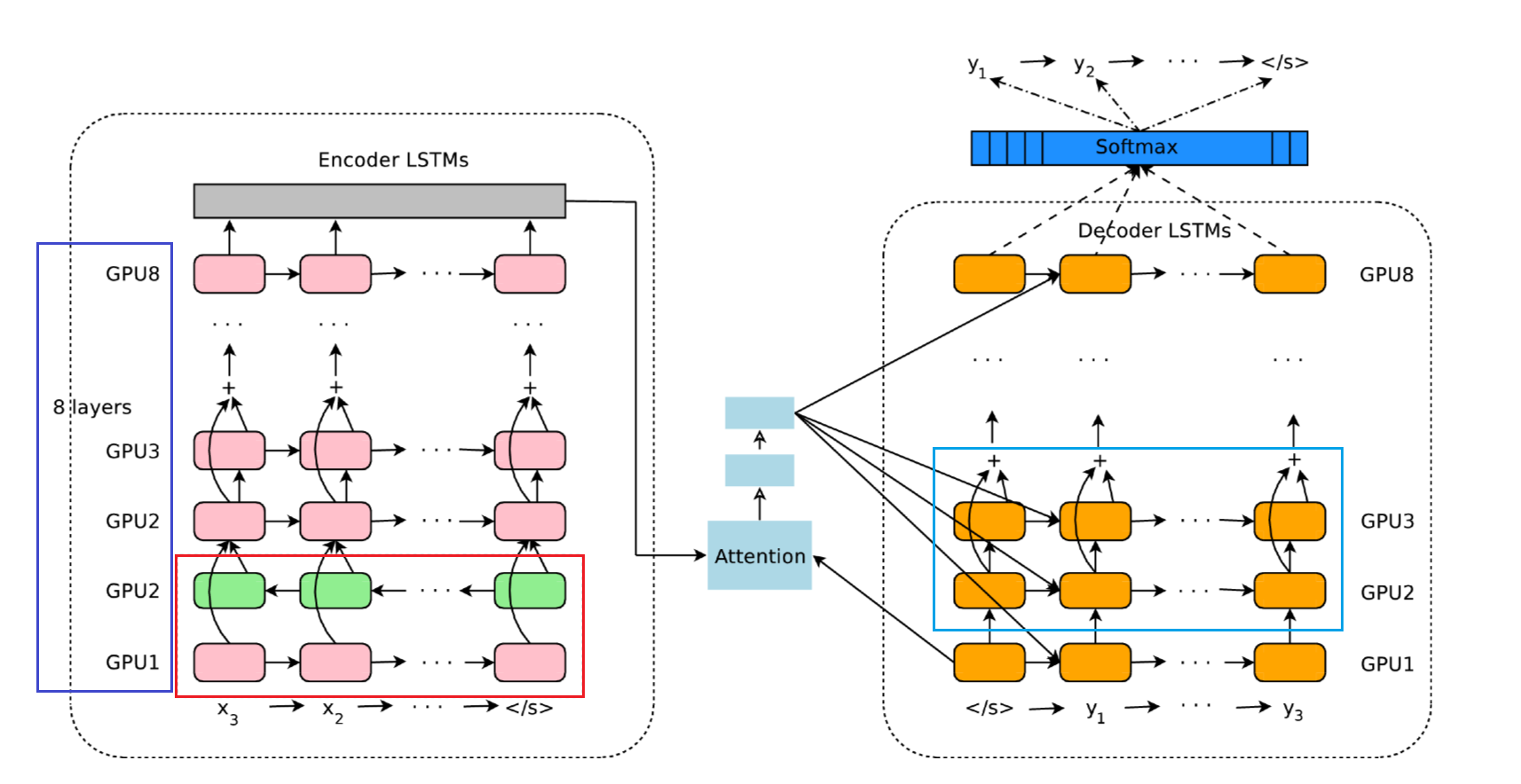
위 그림은 GNMT의 구조를 나타낸 것입니다.

붉은색 네모 부분에서 양방향 LSTM 구조를, 하늘색 네모 부분에서 skip 연결을 사용하고 있는 것을 볼 수 있습니다. 파란색 네모 부분에서는 GPU 1개당 1계층씩 총 8중 레이어를 사용하여 분산 학습하는 구조로 되어 있는 것을 확인할 수 있습니다.

위 그림은 GNMT의 성과를 나타낸 것입니다.

영어->스페인어나, 프랑스어->영어 번역에 있어서는 사람을 거의 따라잡았습니다. 다만, GNMT를 구현하기 위해서는 대량의 데이터와 막대한 컴퓨팅 자원이 필요합니다. (논문에서는 GPU 100여개를 사용하여 모델 하나를 학습하는데 6일이 걸렸다고 적혀 있습니다.)

트랜스포머 Transformer

Attention Is All You Need | 논문 링크

RNN은 (시간 순서 상으로) 과거의 데이터를 현재 연산 과정에 참고하는 재귀적 구조로 설계돼 있습니다. 다시 말해 병렬 연산이 기본적으로 불가능합니다. 과거와 현재를 동시에 계산할 수는 없기 때문이죠. 그래서 RNN을 사용한 연산은 주로 GPU를 사용하는 딥러닝 학습 환경에 매우 비효율적입니다.

한 번쯤 들어봤을 트랜스포머는 이런 문제를 해결한 신경망 모델입니다.

트랜스포머는 RNN 대신 셀프어텐션이라는 기술을 사용합니다. 셀프어텐션은 쉽게 말해 하나의 시계열 데이터 내에서 각 원소끼리의 상관 관계를 살펴보자는 아이디어입니다.

여기서 말하는 '하나의 시계열'이란 태스크 레벨에서 신경망에 입력하는 시계열 데이터의 수를 가리키는 것이 아닙니다. RNN은 '과거의 자기 자신'과 '현재의 자기 자신'이라는 2개의 시계열 데이터를 사용하고, 셀프어텐션은 자기 자신을 분석하는 동시에 보기 때문에 하나의 시계열 데이터를 사용하는 차이입니다.

조금 더 쉬운 설명

전편에서 seq2seq과 어텐션의 차이를 설명서에 비유해 설명했습니다.
두 모델과 트랜스포머의 차이는 바로 설명서를 쓰고 읽는 데 사용하는 손의 개수입니다.

오타가 아닙니다. 컴퓨터는 텍스트를 읽지 못합니다. 컴퓨터가 신경망을 통해 텍스트를 읽는 원리는 시각장애인이 점자를 통해 텍스트를 읽는 것과 같습니다. 그들이 이해할 수 있는 언어로 바꿔주는 것이죠.

seq2seq과 어텐션(정확히는 seq2seq에 적용된 어텐션)은 손이 하나밖에 없기 때문에 설명서를 순서대로 써야 합니다. 읽을 때도 차근차근 읽어야 하죠. 하지만 트랜스포머는 손이 여러 개입니다. 그래서 동시에 설명서의 여러 챕터를 쓸 수도 있고, 읽을 때도 여러 챕터를 동시에 읽을 수 있습니다.

그리고 셀프어텐션이 바로 여러 챕터를 한 번에 쓰거나 읽는 방법에 해당합니다.

셀프어텐션 메커니즘

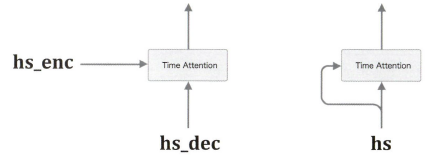
왼쪽은 일반적인 어텐션이고, 오른쪽은 트랜스포머 모델의 셀프 어텐션 과정을 나타낸 것입니다.

트랜스포머 모델도 인코더-디코더 구조를 사용합니다. 대신 시퀀스를 순차적으로 입력받는 RNN과 달리 시퀀스 전체의 정보를 한 번에 입력받는다는 차이가 있습니다.

구체적인 방법은 다음과 같습니다.

트랜스포머 모델의 시퀀스 입력 과정

시퀀스를 여러 개의 토큰으로 쪼갠다.

각 토큰들을 한번에 인코더에 입력한다.

그런데 이 때 각 토큰들이 순차적으로 입력되지 않기 때문에 서로 간의 순서 관계를 알 수 없다는 문제가 발생합니다. 쉽게 말해서 I am a cat과 am I a cat이라는 두 시퀀스를 구분할 수 없다는 것입니다.

트랜스포머는 이를 해결하기 위해 포지셔널 인코딩이라는 기법을 사용합니다.

포지셔널 인코딩은 단어의 임베딩 벡터에 위치 정보 값을 더하는 것입니다.
구체적인 방법은 아래 링크에 잘 소개돼 있습니다.

포지셔널 인코딩 기법 | 링크

포지셔널 인코딩을 통해 위치 정보가 포함된 임베딩 벡터를 입력받은 인코더는 이제 토큰 간의 위치 관계를 알고 있습니다. 그렇다면 남은 할 일은 일반 어텐션과 동일합니다.

일반 어텐션에서는 인코더에서 추출한 전체 시퀀스의 은닉 상태 벡터행렬 $hs$ 와 디코더의 첫 셀의 은닉 상태 $h$ 를 입력받아 두 벡터를 내적해 $s$ 값을 구하고, 이를 정규화하여 가중치 $a$ 를 구한 후 가중합을 사용하여 맥락 벡터 $c$ 를 구했습니다.

그런데 셀프어텐션 계층에서는 이야기가 조금 달라집니다. 동시에 모든 토큰을 입력받았기 때문에 각 토큰의 은닉 상태 $h_1, h_2, h_3, \cdots, h_t$ 를 구하는 것과 각 토큰의 은닉 상태를 모은 벡터행렬 $hs$ 를 구하는 것은 똑같은 연산이 됩니다.

즉, $h = hs$ 가 되는 것입니다.

나는 고양이로소이다라는 시퀀스를 입력받았을 때, 어텐션을 적용한 seq2seq과 셀프어텐션의 $hs$ 를 직관적으로 표현하면 다음과 같습니다.

hs의 n번째 벡터	seq2seq	셀프어텐션
n = 1	'나'의 은닉 벡터	'나', '는', '고양이', '로소', '이다'의 은닉 벡터
n = 2	'나', '는'의 은닉 벡터	'나', '는', '고양이', '로소', '이다'의 은닉 벡터
n = 3	'나', '는', '고양이'의 은닉 벡터	'나', '는', '고양이', '로소', '이다'의 은닉 벡터
n = 4	'나', '는', '고양이', '로소'의 은닉 벡터	'나', '는', '고양이', '로소', '이다'의 은닉 벡터
n = 5	'나', '는', '고양이', '로소', '이다'의 은닉 벡터	'나', '는', '고양이', '로소', '이다'의 은닉 벡터

그렇다면 셀프어텐션의 맥락 벡터 $c$ 는 어떨까요? $h = hs$ 이기 때문에 $s$ 값은 1이 됩니다. 당연히 $a$ 값도 1이 됩니다. 그리고 $a$ 값이 1이면 가중합을 하는 의미가 없습니다. $a$ 가 단위행렬이라는 뜻이기 때문입니다.

결과적으로 $h = hs = c$ 가 됩니다.

셀프어텐션 계층은 이렇게 해서 구한 맥락벡터 $c$ 를 순전파로 전파합니다. 아래 그림을 보면 어떻게 인코더에서 디코더로 전달되는지 살펴볼 수 있습니다.

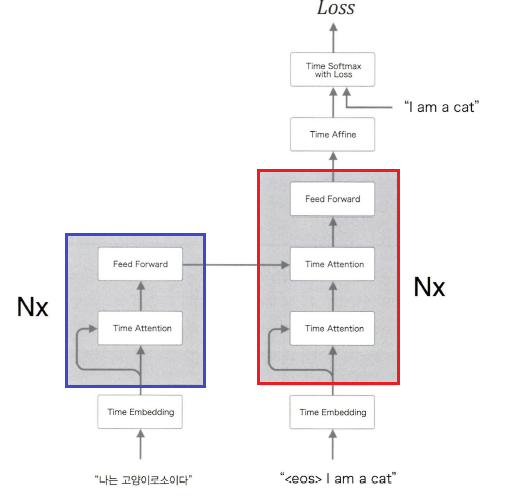
파란색으로 표시된 부분이 인코더이고, 붉은색으로 표시된 부분이 디코더입니다.
Nx는 N개의 인코더와 디코더를 사용한다는 뜻이죠. 각 인코더는 다음 인코더로 자신의 출력 결과를 전달합니다. 마지막 인코더의 출력은 각 디코더에 동시에 전달됩니다. 이를 통해 네트워크를 심층화하는 효과를 얻을 수 있습니다.

위 영상은 트랜스포머의 작동 흐름을 나타낸 것입니다.
자세히 보면 인코딩 뿐 아니라 디코딩 과정에서도 셀프어텐션이 이뤄지는 것을 볼 수 있습니다.

멀티 헤드 어텐션

논문에서는 하나의 어텐션을 여러 개의 서브 어텐션으로 나누어 병렬 연산한 후 결과값을 병합해 사용합니다. 이걸 멀티 헤드 어텐션이라고 합니다. 이를 위해서 몇 가지 하이퍼파라미터가 존재합니다. 논문에서 제시한 트랜스포머의 하이퍼파라미터들은 다음과 같습니다.

트랜스포머의 하이퍼파라미터

아래의 하이퍼파라미터별 값은 논문에서 사용한 수치입니다.

$d_{model}$ = 512
인코더 & 디코더에서 사용하는 입출력 크기입니다. 임베딩 벡터의 차원 크기이기도 합니다. 각 인코더가 다음 인코더/디코더로 출력을 전달할 때도 shape가 유지됩니다.

num_layers = 6
인코더와 디코더의 총 층수입니다. Nx에서 N에 해당합니다.

num_heads = 8
하나의 어텐션 계층을 구성하는 서브 어텐션 계층의 수입니다.

$d_{ff}$ = 2048
트랜스포머 내부 순전파(피드 포워드)의 은닉층의 크기입니다. 당연히 입/출력층의 차원 수는 $d_{model}$ 입니다.

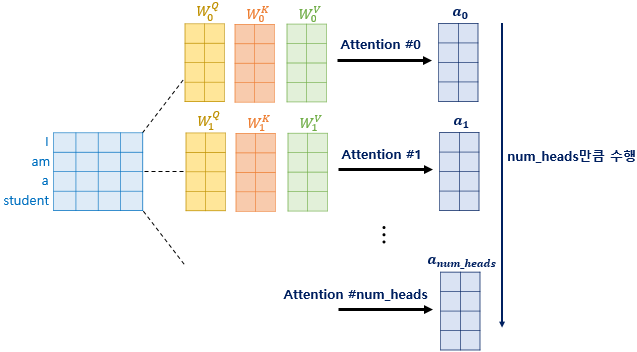
1개의 인코더는 num_heads개의 서브 어텐션을 갖습니다. 구체적으로는 임베딩 벡터를 서브 어텐션의 수만큼 쪼개서 병렬로 어텐션을 수행합니다. 따라서 각 서브 어텐션에서 사용하는 입출력 크기는 ( $d_{model}$ / num_heads)가 됩니다. 당연히 각각의 서브 어텐션마다 연산 과정에서 구해지는 가중치 값도 달라지겠죠.

이는 임베딩 벡터를 num_heads 수만큼의 관점으로 분석하는 것과 같습니다.

위 그림을 보면 멀티 헤드 어텐션의 효과를 직관적으로 알 수 있습니다.

it이 쿼리라고 가정해보겠습니다.

The animal didn't cross the street because it was too tired 라는 시퀀스의 임베딩 벡터가 512개의 차원을 가진 상태로 인코더에 들어갑니다. num_heads가 8이므로 전체 시퀀스 임베딩 벡터는 (512/8) = 64개씩 8조각으로 나뉘게 됩니다. 64개의 차원을 가진 각 조각들은 서브 어텐션 계층으로 다시 들어가서 각각의 맥락 벡터 $c_1, c_2, c_3, \cdots, c_8$ 로 변환됩니다.

이렇게 추출된 각 맥락벡터를 병합하면 전체 시퀀스를 8개의 관점에서 분석한 맥락 벡터 $c_{seq}$ 가 만들어집니다. 당연히 $c_{seq}$ 의 shape는 ( $len_{seq}$ , $d_{model}$ )이 되겠죠?

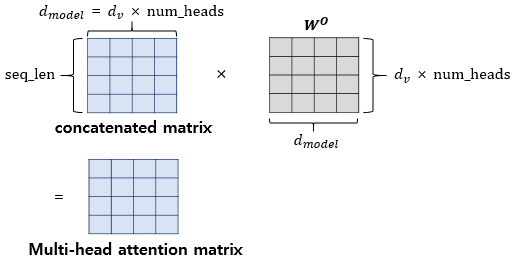
여기서 끝이 아닙니다. 아직 병합된 맥락 벡터 $c_{seq}$ 를 전파하는 단계가 남아있습니다. 따라서 $c_{seq}$ 에 가중치 행렬 $W_0$ 를 곱해주어야 합니다. 위 그림을 보면 맥락 벡터의 형상이 바뀌지 않는다는 것을 알 수 있습니다.

이상의 과정을 통해 인코더에서 추출된 맥락 벡터 $c_{enc}$ 를 디코더에 집어넣으면 it과 가장 유사한 벡터를 찾을 수 있습니다. 여러 관점을 고려하기 때문에 그만큼 표현력이 올라가는 것입니다.

뉴럴 튜링 머신 (NTM)

RNN이나 LSTM은 내부적으로 시퀀스의 은닉 벡터 상태를 기억합니다. 앞서 살펴본 $h$ 나 $hs$ 가 이에 해당하죠. 컴퓨터에 비유하면 캐시 메모리의 역할을 한다고 볼 수 있습니다.

그런데 현실의 컴퓨터는 캐시 메모리만 있는 게 아닙니다. HDD도 있고, SDD도 있고, USB같은 외장 메모리도 있죠. 앞에서 인코더는 컴퓨터가 읽을 수 있도록 설명서를 만들고, 디코더는 설명서를 따라 데이터를 읽는다고 했습니다. 컴퓨터의 메모리 입출력 구조와 비슷하지 않나요?

이처럼 어텐션을 활용하여 RNN 외부에 메모리를 배치하고, 어텐션으로 저장하거나 읽어오는 연구들 중에서 유명한 것이 뉴럴 튜링 머신(NTM)입니다.

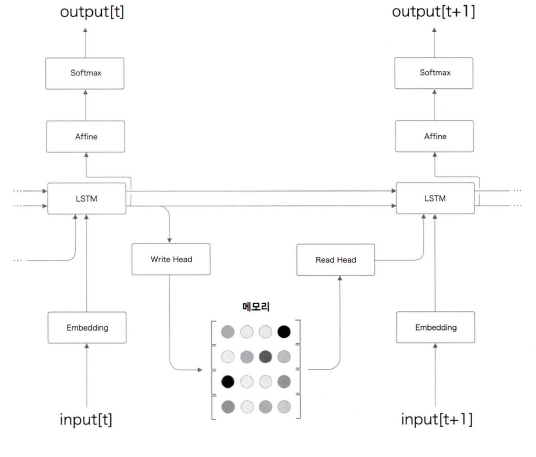
위 그림을 통해 NTM의 구조를 살펴볼 수 있습니다.

앞에서 살펴본 어텐션을 추가한 seq2seq 모델과 비슷하지만, 두 LSTM 계층 사이에 입출력 기능이 추가되었습니다. 일반적인 컴퓨터는 프로그램을 통해 작동합니다. 프로그램은 사전에 지시된 명령들로 이뤄져 있죠. 하지만 NTM은 학습을 통해 작동합니다. 그렇기 때문에 '뉴럴 튜링 머신' 인 것입니다. 여기서는 간단하게 개념만 설명하겠습니다.

NTM은 메모리 조작을 위해 콘텐츠 기반 어텐션과 위치 기반 어텐션을 사용합니다.

콘텐츠 기반 어텐션은 지금까지 본 어텐션과 동일한 메커니즘입니다. 입력으로 질의(query) 벡터가 주어지면, 이와 유사한 벡터를 메모리로부터 찾아냅니다. 데이터베이스에서 쿼리를 사용해 데이터를 추출하는 것과 비슷합니다.

반대로 위치 기반 어텐션은 이전 시각 $t-1$ 에서 주목한 메모리의 위치를 기준으로 전후 이동하는 역할을 수행합니다. 특정 메모리 위치를 '선택'하는 작업을 한다는 뜻입니다. 실제 컴퓨터도 메모리 주소를 찾아서 움직이며 I/O가 이뤄지죠.

Neural Turing Machines | 링크

NTM에 대한 더욱 자세한 기술적 설명은 위 링크의 논문을 참고하면 됩니다.

Ethan

재미있게 살고 싶은 대학원생

이전 포스트

[딥러닝] 어텐션 Attention 1

다음 포스트