[DL models A-to-Z] 1주차. CNN

Nopego Keepgo·2023년 3월 13일
AICNNDeepLearningResnetVGGNetbasic
2

[AI Models A-to-Z]

목록 보기
1/2
post-thumbnail
*밝게 보시는걸 추천드립니다.
*잘못된 내용은 말씀해주시면 편하게 말씀해주셔도 됩니다.

0. Intro

  • Deep Learning의 각 분야들의 basic들을 다루는 시리즈를 만들기에 앞서서, 가장 먼저 어떤 논문을 다루면 좋을지 고민해보았다.
  • 고민은 그리 오래 가지 않았다. 사실 Deep Learning을 배우는 어느 수업을 가든, 또는 독학을 하든 항상 처음 만나게 되는 모델은 바로 CNN의 대표적인 모델들인 VGGNet과 ResNet이다.(물론 neural perceptron과 back propagation과 같은 딥러닝의 기본적인 컨셉을 안다는 전제하에서 말하는 것이다.)
  • 따라서, [DL models A-to-Z]의 가장 첫번째 포스팅은 다음과 같은 순서로 CNN에 대해서 얘기해보려 한다.

    1. MLP basic

    • CNN을 다루기에 앞서서 Deep Learning의 근간이 되는 Fully Connected layer의 개념을 알아본다.

    2. CNN is channel-wise 2D MLP

    • CNN은 결국 위치정보를 보존하는 MLP라 얘기할 수 있다.

    3. VGGNet: Depth is all we need.

    4. ResNet: Ok, then Deeper network, better nerwork?

1. MLP basic

1.1 Perceptron

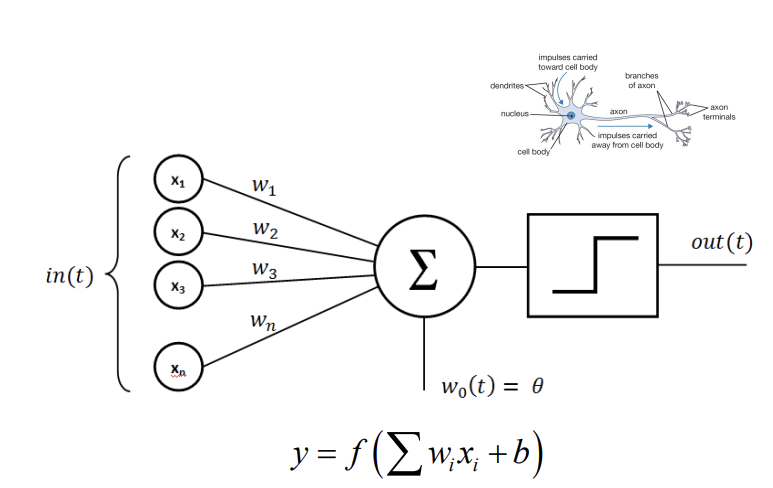
  • 위 그림은 Deep Learning 분야를 공부하게 되면, 수도 없이 보게 되는 그림이다.
  • 저 cell 하나를 우리는 퍼셉트론(perceptron), single node, 등 여러가지 이름으로 부른다.

이를 classification에서 생각해보자.

우리는 다음과 같은 n개의 attribute를 갖는 벡터들(즉, data 1개)을 2개의 class로 분류하는 분류기를 학습하고자 할때 다음과 같은 decision boundary들을 그릴 수 있을 것이다.

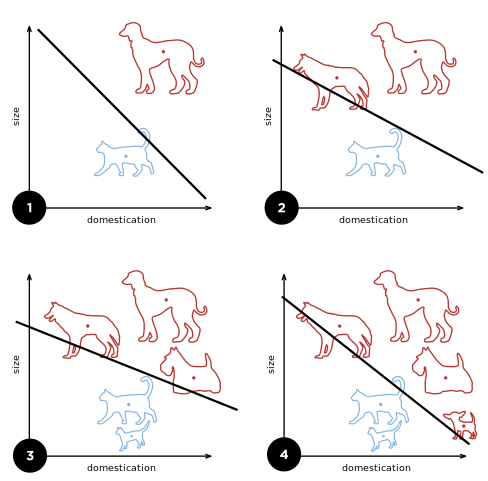
  • 여기서 그림에서 확인할 수 있는 것처럼, 한 데이터는 2개의 attribute(또는 feature) size와 domestication을 가지고 있고, 이 두 개의 attribute에 의해 linear한 boundary가 위와 같이 그려지게 된다.
  • SLP 하나의 의미는 결국 이 attribute들이 이루는 차원공간내에 존재하는 data들에 대하여 이들을 나누는 decision boundary를 학습하겠다는 뜻으로 생각할 수 있다.
  • 앞서서 SLP 내에서 학습한 w1,w2w_1,w_2를 통해 전체 차원공간을 "개"의 공간과 "고양이"의 공간으로 분할할 수 있게 되고, 이를 통해 decision boundary를 구하게 되는 것이다.


    SLP 하나의 의미는 결국, 어떤 데이터의 attribute들인 x1,x2,...xnx_1,x_2,...x_n로 부터, 어떤 data들을 분류할 수 있는 weight w1,w2,...wnw_1, w_2, ...w_n을 구하여 전체 attribute 차원을 나누는 linear한 decision boundary를 찾는 것이라고 생각할 수 있다.

1.2 MLP

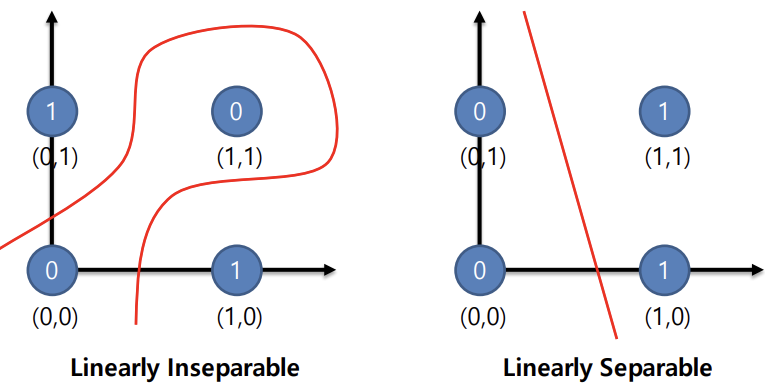
  • 그렇다면, 위와 같은 dataset은 어떻게 분류해야할까. 앞선 perceptron 하나는 Linear한 decision boundary 하나를 찾을 수 있기 때문에, 좌측과 같은 non-linear한 classification문제에는 적용하기 힘들다.
  • MLP(Multi-layer Perceptron)의 아이디어는 이러한 non-linear decision boundary를 찾는데에서 출발하였다.

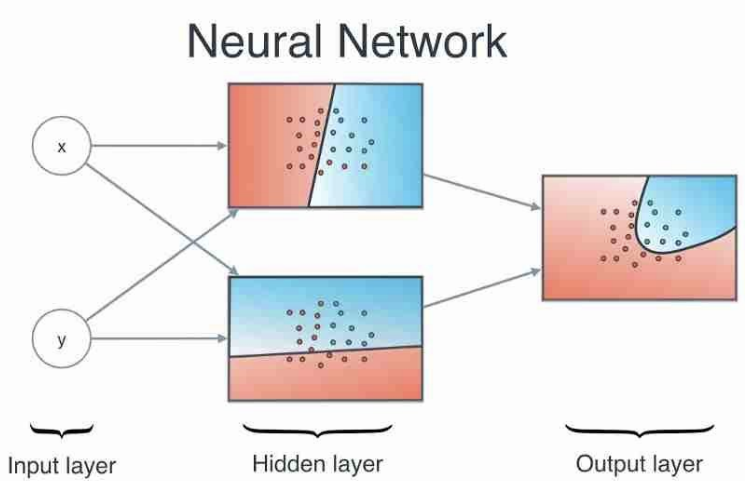
  • 위와 같이, 서로 다른 두 개의 perceptron(또는 node)를 구성한 뒤에 이를 종합해서 decision boundary를 예측하는 구조는 non-linear한 dataset에 대해서도 분류할 수 있을 것이다.
  • 더 나아가, 위 그림처럼 위아래로 쌓는 것이 아니라, 옆방향으로도 perceptron을 쌓게 되면 전체 network의 비선형성을 더해줄 수 있을 것이다.

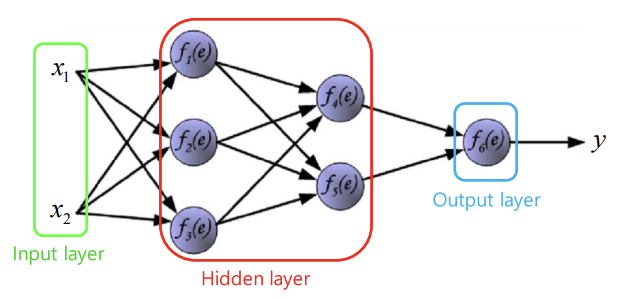
  • 이렇듯, 선형적으로 예측하는 perceptron 여러개를 쌓아 비선형성을 가지게 만든 구조를 MLP (또는 Forward Network, Dense Network, Fully-Connected layer)라고 한다.
  • 비선형성과 MLP에 대해 구체적으로 살펴보려면, loss function이나 backpropagation에 대해서도 살펴봐야하지만 여기서는 생략하겠다.

여기까지 CNN을 얘기하기 위한 MLP의 컨셉에 대해 간단하게 살펴보았다. 일단 여기서 다른 부분보다도 CNN을 얘기하기 위해 이해해야할 점은 2가지다.
  1. perceptron 1개는 결국 각 input feature들에 weight를 곱하고 더하여, 값 1개를 linear하게 특징값 한개를 뽑아낸다.
  2. 이러한 perceptron을 여러개 쌓은 MLP는 결국, "서로 다른 방식으로 input feature들을 바라보는 perceptron들"을 통해 여러 특징값들을 뽑아내고, 이들을 반복적으로 쌓아서 더 복잡하고 비선형적인 예측도 가능하게 한다.

2. CNN is channel-wise 2d-MLP

2.1 2-d Convolution

x(t)∗f(t)=∑τx(τ)f(t−τ)x(t)*f(t)=\sum_{\tau}x(\tau)f(t-\tau)
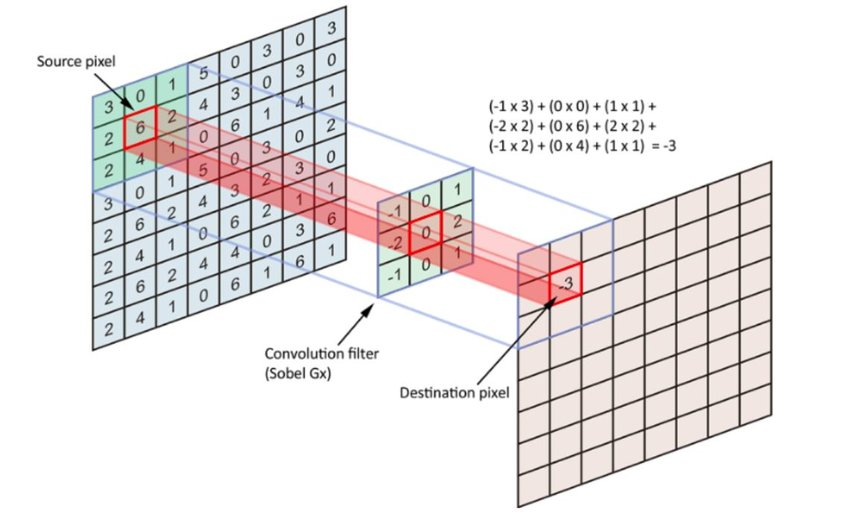
  • 위 convolution 수식은 공대생이면, 한 번쯤은 봤을 법한 수식이다.
  • Convolution의 본래의 의미는 어떤 고정된 filter f(t)를 signal x(t)에 대하여 전체 domain에서 τ\tau씩 이동하여 곱하고 더하여, 말 그대로 filter에 따라 x(t)를 변환시키는 filtering는 의미이다.
  • 2-d convolution은 단순히, 이러한 filtering을 2차원에서 mapping하는 것으로 이해할 수 있다.

  • CNN이 나오기 이전에도 convolution을 이용하여 image로부터 원하는 feature를 extract하는 여러 알고리즘들은 존재했다.
  • 다만, CNN과의 차이점은, 여기서 사용되는 filter들이 학습이 아니라, 인간이 직접 만든(handcrafted) filter라는 점이다.

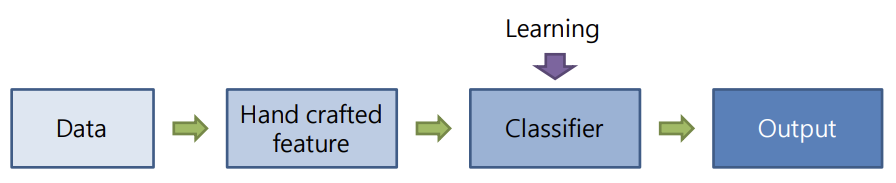
  • 즉, CNN이전에는 input image로부터 handcrafted filter를 통해 feature들을 뽑아내면, 이를 MLP에 통과시켜서 classification을 하는 방식으로 학습을 했던 것이다.


    CNN은 이러한 filter에 대한 학습 가능성에서 비롯되었다.

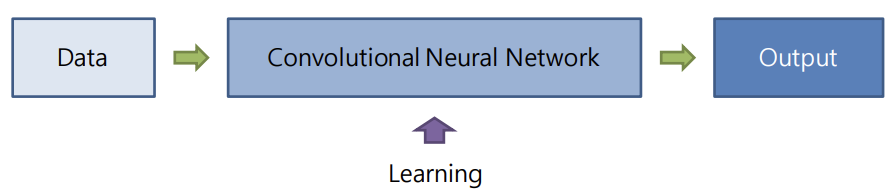
  • 앞서서 SIFT나 HOG와 같은 filter들이 task에 맞는 feature를 뽑아내듯이, 각 task에 맞는 filter가 존재한다고 가정해볼 수 있을 것이다.

  • 즉, 우리가 원하는 task에 맞는 feature extracting을 담당하는 filter를 backpropagation을 통해 컴퓨터가 찾아내는 과정이 바로 CNN인 것이다.

2.2 1x1 Convolution layer vs. Fully-Connected layer

Convolution의 계산과정을 정확하게 이해했다면 답변을 가리고 다음의 질문에 대해 고민해보자.

Question. 1x1 Convolution과 Fully-Connected layer의 차이점과 공통점은 무엇일까?

  • 사실 앞서서 챕터 소개에서 눈치챘겠지만 정답은 "둘은 같다."이다. 계산 과정에 있어서 둘은 전혀 차이가 없다.

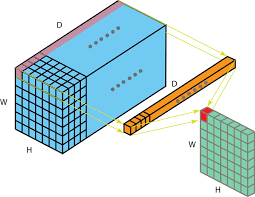
  • 1x1 Convolution에서 channel을 FC layer 1층의 input node수, filter수를 output node수로 보면 둘의 연산 과정은 완전히 같다. filter 한개가 전체 channel로부터 output node 한 개를 뽑아낸다고 생각하면 이해하기 쉽다.

  • 앞서서 MLP에서 node 한개는 결국 주어진 feature를 해석하는 하나의 방식이라 했다. 이는 결국 CNN에서도 적용되어 각 channel들은 주어진 이미지들에 대한 2d 형태의 feature이며 filter들은 이러한 channel들을 해석하는 여러 관점들로 생각할 수 있게 된다.

  • 이는 1x1 Convolution이 아닌 다른 nxn Convolution에 대해서도 단순히 feature가 2d형태인 것으로 확장하면 똑같이 이해할 수 있게 된다.

정리

  1. CNN은 우리가 원하는 task에 맞는 feature를 가장 잘 출력할 수 있는 filter를 찾는 과정이다.
  2. CNN은 결국 MLP를 channel-wise하게 MLP를 적용한 것으로 확장시킬 수 있는데 다음과 같은 방식으로 MLP와 대칭적이다.
    • channel: input 2d-features
    • filter: output nodes(각각의 노드는 weight가 다른 것처럼 filter역시 각 channel에 곱하는 weight가 다른 것 생각하자!)

3. VGGNet

4. ResNet

profile
Nopego Keepgo
Majoring in EE
다음 포스트

[ML models A-to-Z] Week2. Spatial Transformer Networks

0개의 댓글