CNN
CNN은 Convolution Neural Network 의 약자로, 딥러닝에서 이미지나 영상 데이터 처리시 주로 쓰이는 모델입니다.
우선 CNN의 이름에서 알 수 있듯이 Convolution이라는 이미지 데이터의 전처리 작업이 적용되는 신경망 모델입니다.
일반적인 DNN(Deep Neural Network)는 1차원 형태의 데이터를 사용합니다.
그런데 2차원 형태의 이미지가 입력값이 되는 경우 flatten시켜서 한줄 데이터로 만들어주면서 이미지의 공간적, 지역적 정보가 손실됩니다.
예를들어
[1,0,0][0,1,0]
[0,0,1]
의 경우 대각선의 모양이라는걸 시각적으로 인식 할 수 있지만,
[1,0,0,0,1,0,0,0,1]
의 경우에는 대각선의 특징이 보이지 않게 됩니다.
이러한 문제점에서 시작된 해결책이 CNN 입니다.
CNN은 이미지를 그대로 받아서 공간적, 지역적 정보를 유지한채로 특성들을 파악합니다.
이미지 전체보다 부분을 보고, 이미지의 한 픽셀과 주변 픽셀들의 연관성을 살려서 공간적, 지역적 정보를 살려줍니다.
원리
위에서 이야기한 것 처럼 2차원 이미지는 픽셀 단위로 구성되어 있습니다.
예를 들어 이미지가 30X30 단위의 픽셀로 이루어져 있다면,
우리는 numpy모듈을 이용해 30X30의 행렬로 표현할 수 있습니다.
우리는 이런 방식으로 이미지를 행렬로 표현해 input으로 사용합니다.
필터(kernel)
cnn에서는 인풋 데이터보다 훨씬 작은 사이즈의 필터가 존재합니다.
이 필터가 인풋 데이터를 전체적으로 훑어줍니다.
이 필터는 예를들면 3X3의 크기로
[1,0,1][1,0,1]
[1,0,1]
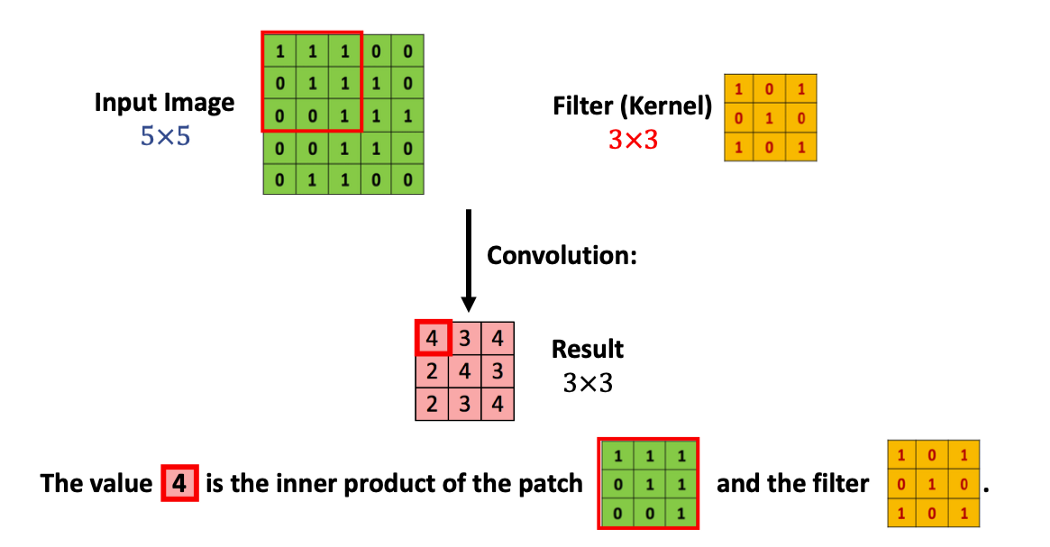
로 생긴 커널을 사용해 Inner Product(내적) 연산처리를 해줍니다.
내적이란 같은 크기의 두 행렬을 놓고 각 위치에 있는 숫자를 곱해 모두 더해주는 연산입니다.
그러면 이 내적 연산을 통해 나온 값들을 가지고 어떤 결과를 만든다는 것일까요?
바로 기존의 인풋 데이터 행렬을 축소해주는 것입니다.
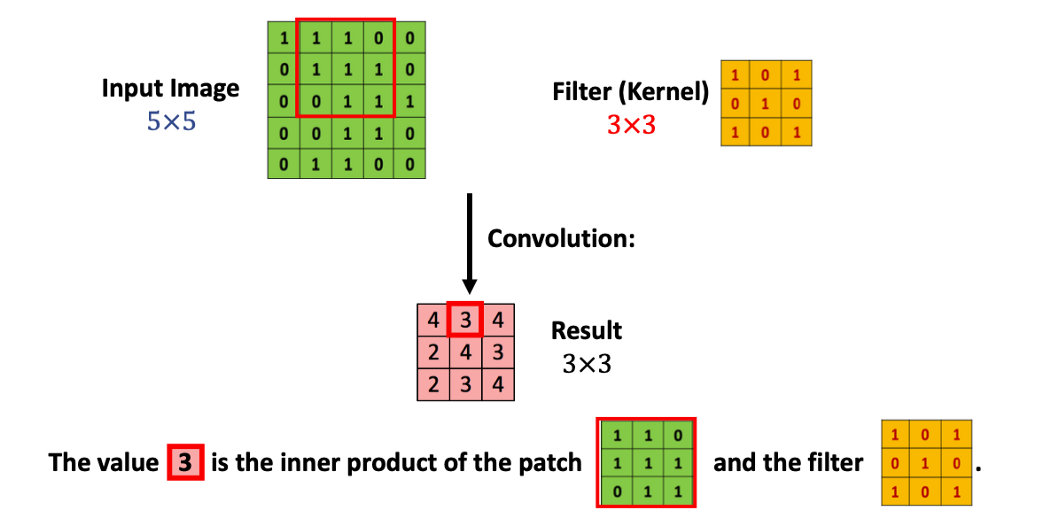
위 사진과 같이 5X5의 행렬을 3X3커널로 훑어주면서 내적값을 구해서 만든 행렬이 result입니다.
위 연산과정을 convolution 이라고 합니다.
결과값 행렬의 크기(차원)은 3X3인데, 5의 너비를 3의 너비로 이동을 할 때,
3번씩 놓을 수 있기 때문입니다.
입력데이터의 크기와 커널의 크기를 가지고 결과 값의 크기를 계산하는 식은 아래와 같습니다.
d1Xd2(input data dimension)
k1xk2(kernel dimension)
결과 값 : (d1-k1+1)X(d2-k2+1)
Zero Padding
위에서 Convolution 처리를 해주었더니 이미지 데이터의 크기가 줄어드는 것을 알 수 있었습니다.
차원이 줄어들면 당연히 손실되는 부분이 발생합니다.
그런 부분을 해결하기 위해서 Padding을 사용할 수 있습니다.
0으로 구성된 테두리를 만들어줍니다.
예를들어
[1,0,1,0,1][0,0,0,0,0]
[1,1,1,0,0][1,1,1,1,1]
[1,0,0,1,1]
일 경우
[0,0,0,0,0,0,0][0,1,0,1,0,1,0]
[0,0,0,0,0,0,0][0,1,1,1,0,0,0]
[0,1,1,1,1,1,0][0,1,0,0,1,1,0]
[0,0,0,0,0,0,0]
로 0으로만 이루어진 테두리로 차원을 늘려주는 방식입니다.
이렇게 padding을 넣어준 뒤 convolution을 해 줄 경우,
(5-3+1)X(5-3+1) 에서
(7-3+1)X(7-3+1) 로 바뀌어서 인풋 데이터와 크기가 같은 결과 값을 얻을 수 있습니다.
이러한 방식으로 손실을 없앨 수 있습니다.
Stride
Stride는 필터가 움직이는 정도를 말합니다.
Stride값이 1일 경우 필터를 한 칸씩 움직여 준다고 생각하면 됩니다.
여태까지 위에서 했던 예시들은 stride가 1입니다.
1이 기본값이고, 그보다 크게 설정할 수 있습니다.
stride값이 커질 경우 필터가 이미지를 건너뛰는 칸이 커짐으로써,
결과 값 이미지의 크기는 작아집니다.
위에서 얘기했던 결과 값 크기의 계산식에 stride를 적용하면 아래와 같습니다.
d1Xd2(input data dimension)
k1xk2(kernel dimension)
결과 값 : ((d1-k1)/s+1)X((d2-k2)/s+1)