n단계 TD방법을 사용할 때 n은 몇으로 해야할까?
평균내는 방법은 어떨까?
미래를 내다봐야 하며, 복잡한 TD, MC 방법을 간단하게 바꿀수는 없을까?
λ 이득(평균 이득)
여기서 사용할 λ 이득의 개념을 설명하겠다.
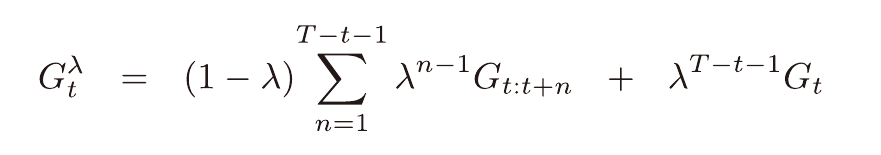
n에 따른 이득을 가중평균하는 식이다.
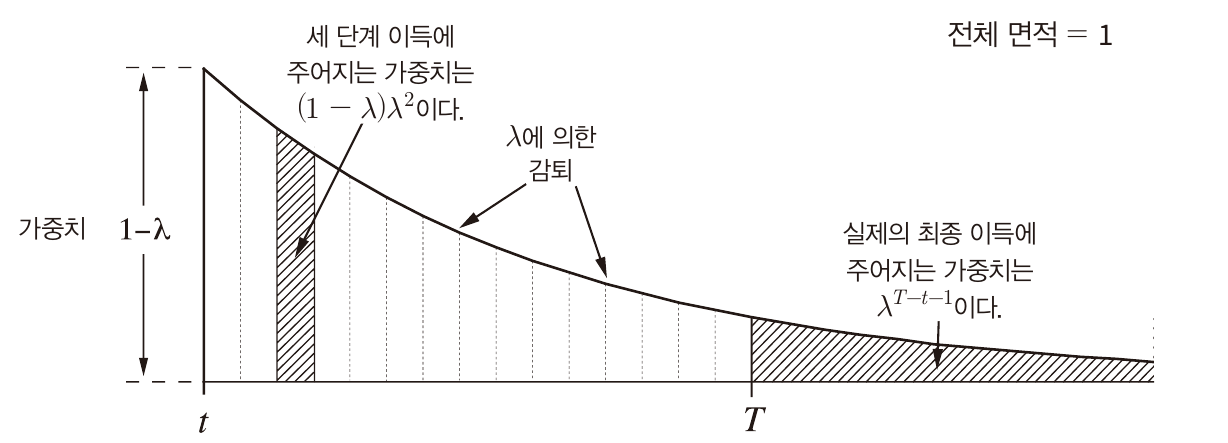
λ에 따라서 가중치가 감소된다.
오프라인 λ 이득 알고리즘
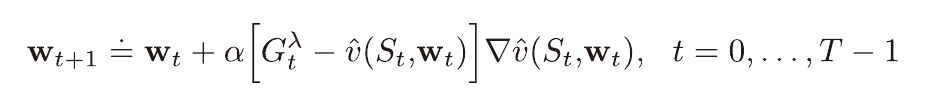
위 λ 이득을 이용한 알고리즘이다.
평균을 내기 위하여 에피소드가 끝날때 까지 기다려야 한다.
적격 흔적, TD(λ)
적격 흔적 벡터를 사용하면 n에 따른 TD방법부터 몬테카를로 방법까지 평균이득을 사용함으로써 일반화 시킬수 있다.
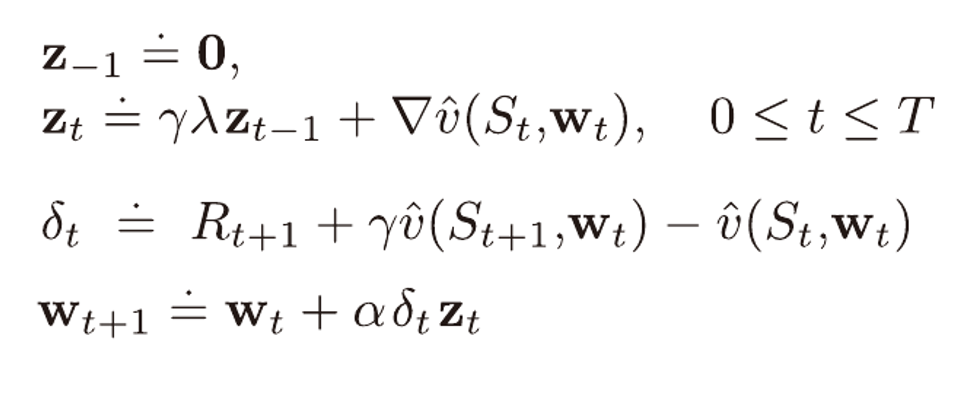
Z를 적격 흔적 벡터라고 부른다.
λ가 0일시 위 알고리즘은 TD(0), 0단계 TD방법이다.
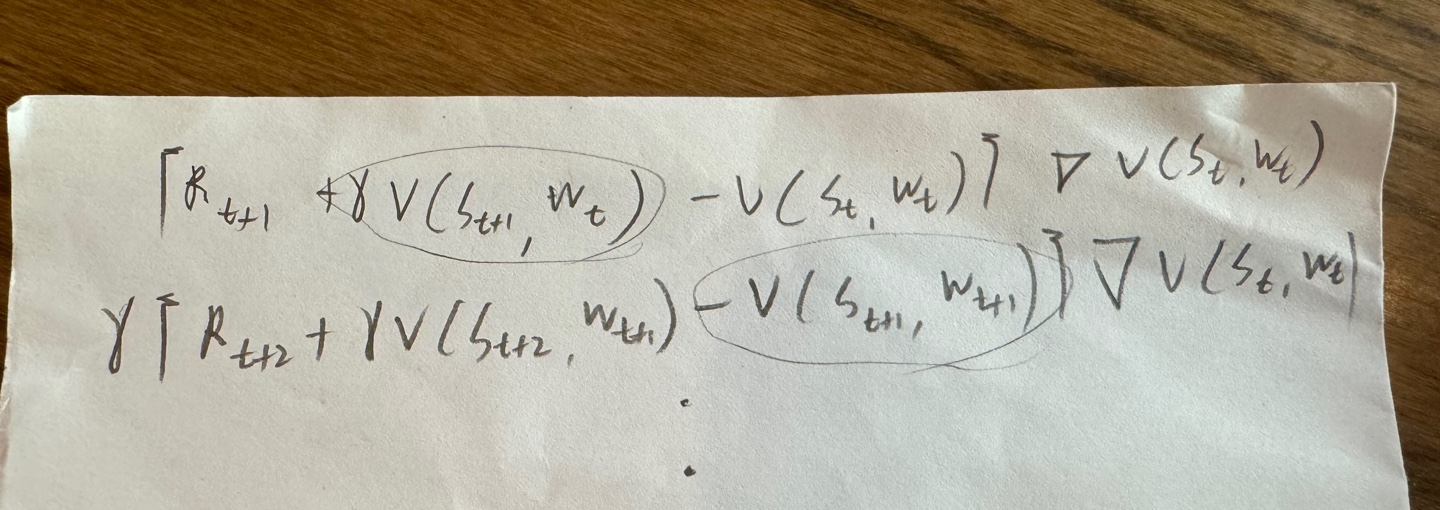
λ가 1일때에는 몬테카를로 방법과 같다.
다른점이 있다면 몬테카를로 방법과 달리 실시간으로 학습이 가능하다는 점이다.
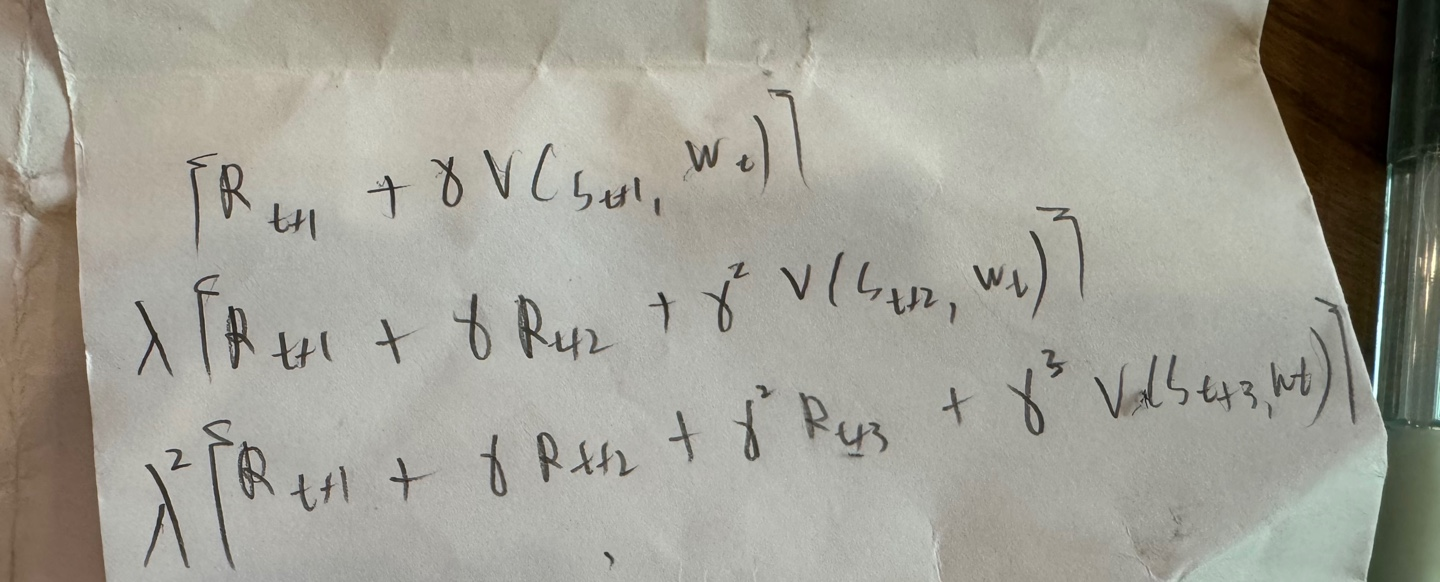
λ가 0~1 사이의 값을 가질때에는 λ 이득(위에서 설명)을 사용하는 것과 같아진다.
중단된 n단계 λ방법
n에 따라 무한히 지속되는 λ 이득을 사용하는 대신 중단된 n단계 λ방법이 있다.
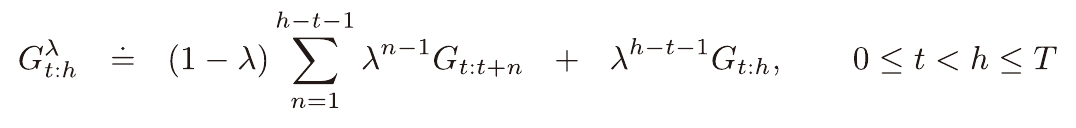
(h단계에서 중단될 시 이득)
이때의 이득은 위와 같이 정의되며, n단계 TD와 같이 첫 n단계동안 갱신이 지연되고 위 이득을 이용하여 한번에 갱신이 시작된다.
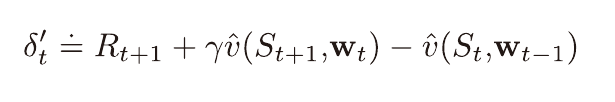
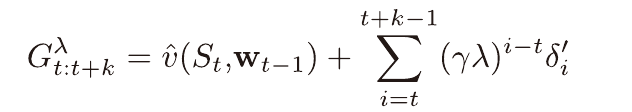
온라인 λ 이득 알고리즘
오프라인 λ 이득 알고리즘은 에피소드가 끝난 뒤, 아래와 같은 방법으로 가중치가 업데이트 된다고 볼 수 있다.
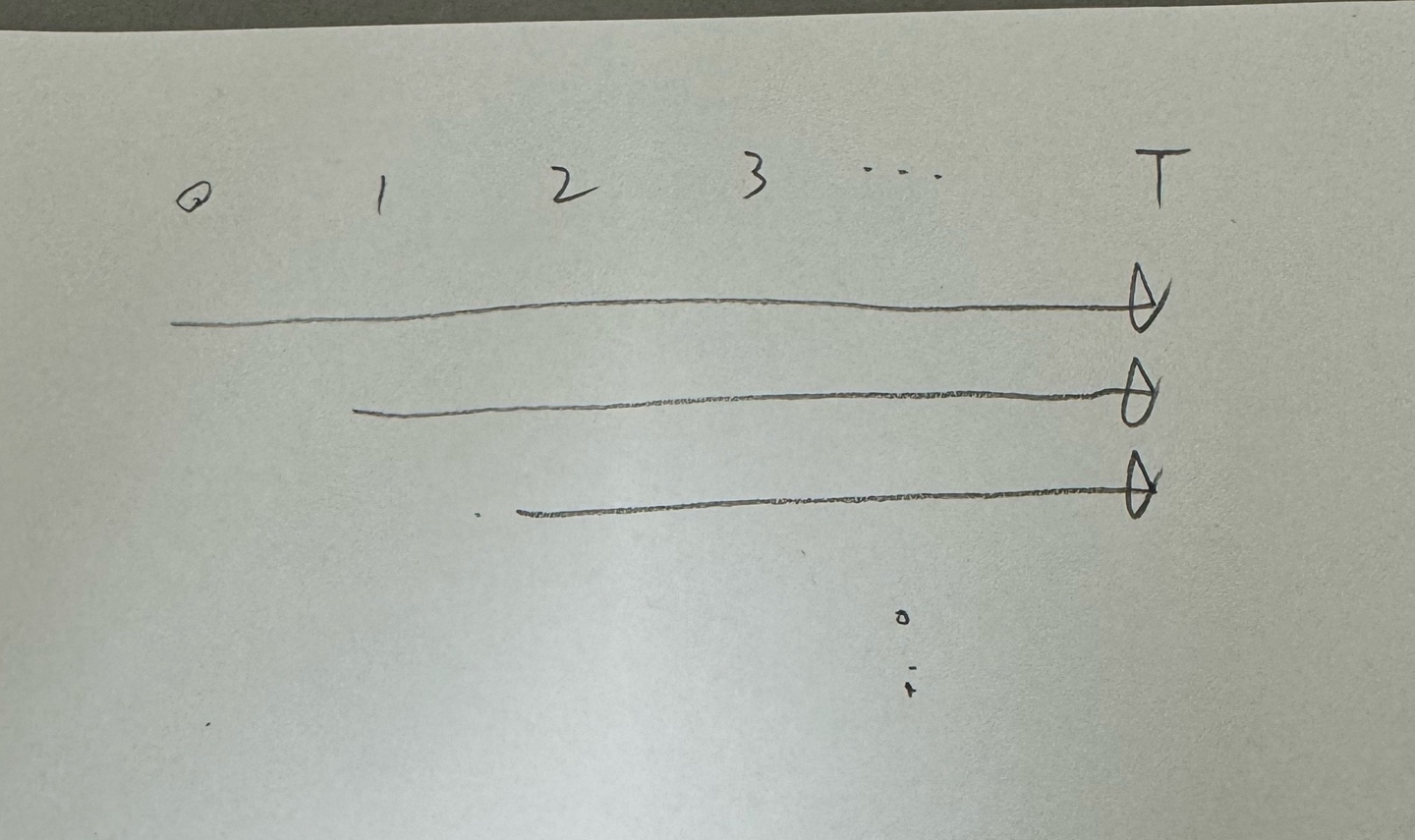
온라인 λ 이득 알고리즘은 실시간으로 업데이트 하는 알고리즘이다.
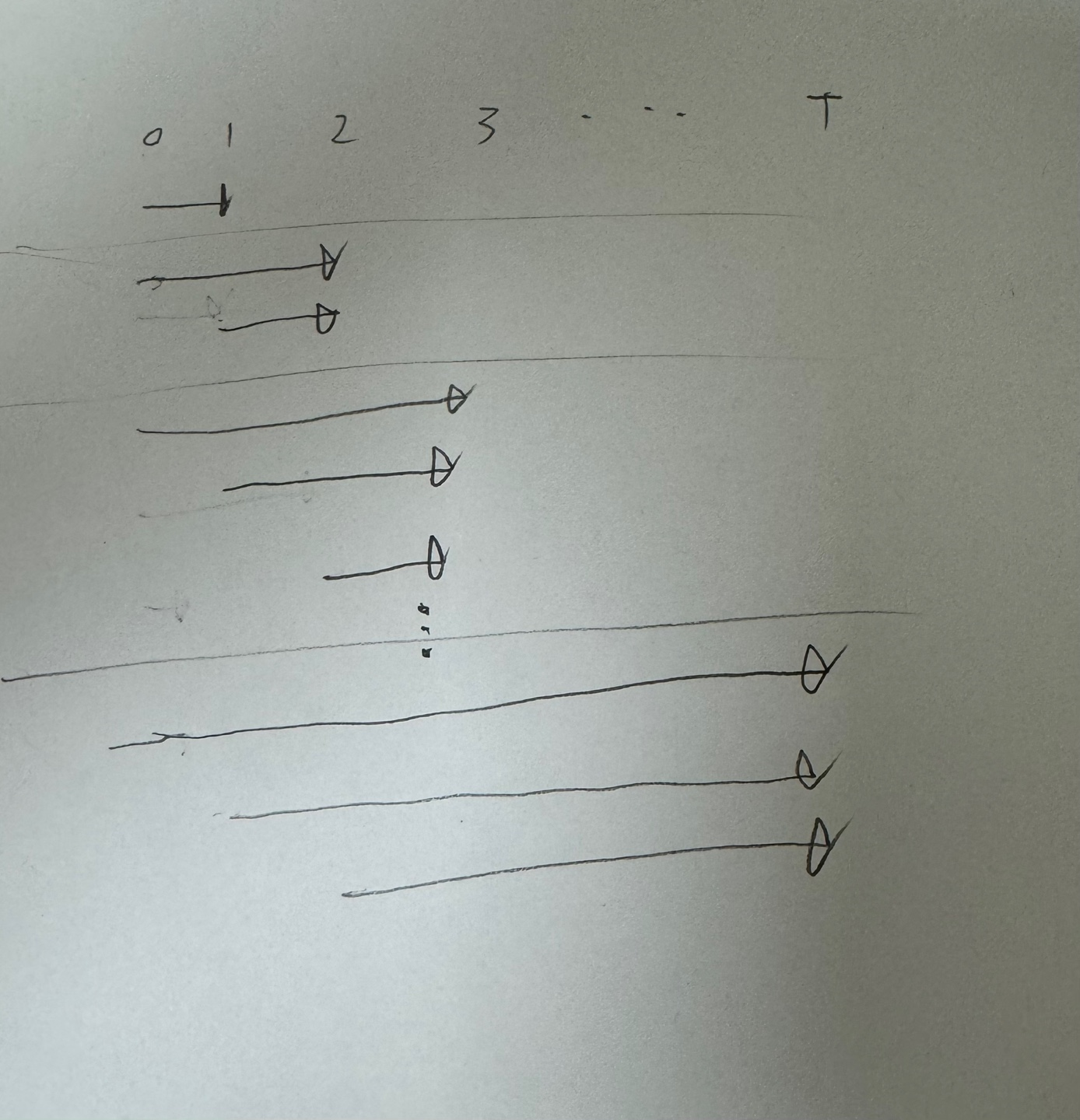
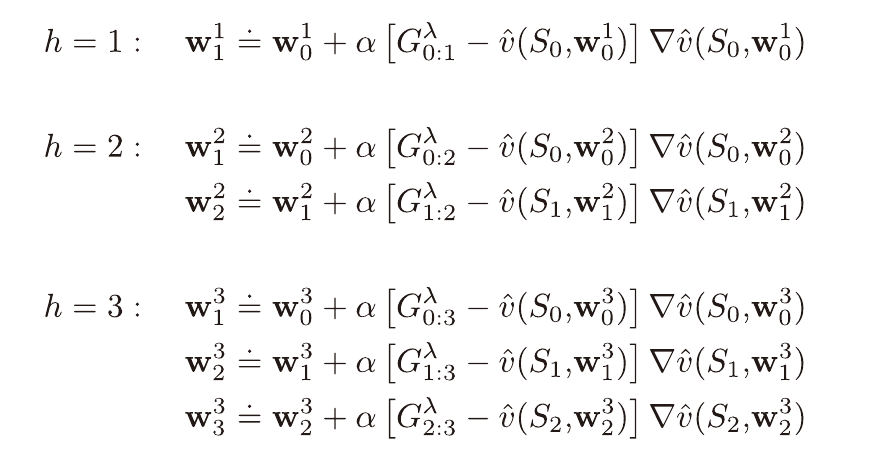
중간단계의 w는 표본 생성을 위해, 부트스트랩을 위해 사용될 뿐
매 단계(h)마다 처음의 가중치를 이용하여 오프라인 λ 이득 알고리즘을 처음부터 반복한다.
(아래 수식을 보면 w1,1이 h=2일때의 수식에 포함되지 않는 것을 볼 수 있다.)
이로써 오프라인 λ 이득 알고리즘을 실시간으로, 더 좋은 성능을 낼 수 있다.
하지만 이 방법은 적격흔적 방법과 달리, 미래를 바라봐야 하며 또한 매우 복잡하다.
True Online Temporal-Difference Learning
v(s,w) = wx(s)로 선형인 경우에는 아래 적격흔적을 사용하는 알고리즘이
온라인 λ 이득 알고리즘을 구현한다는 것이 증명됐다고 한다.
https://arxiv.org/abs/1512.04087 (찾는데 힘들었음)
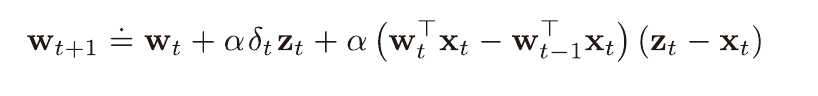
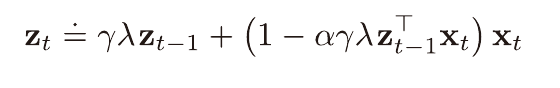
적격 흔적 성능
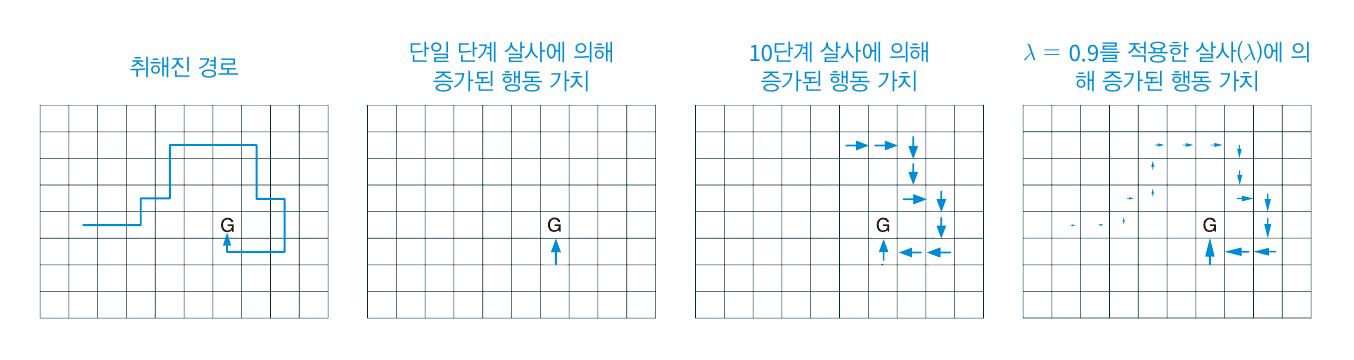
간단할 뿐 아니라, 평균 이득을 사용함으로써 성능 면에서도 이점이 충분함을 확인할 수 있다.
