Machine Learning: 비지도 학습

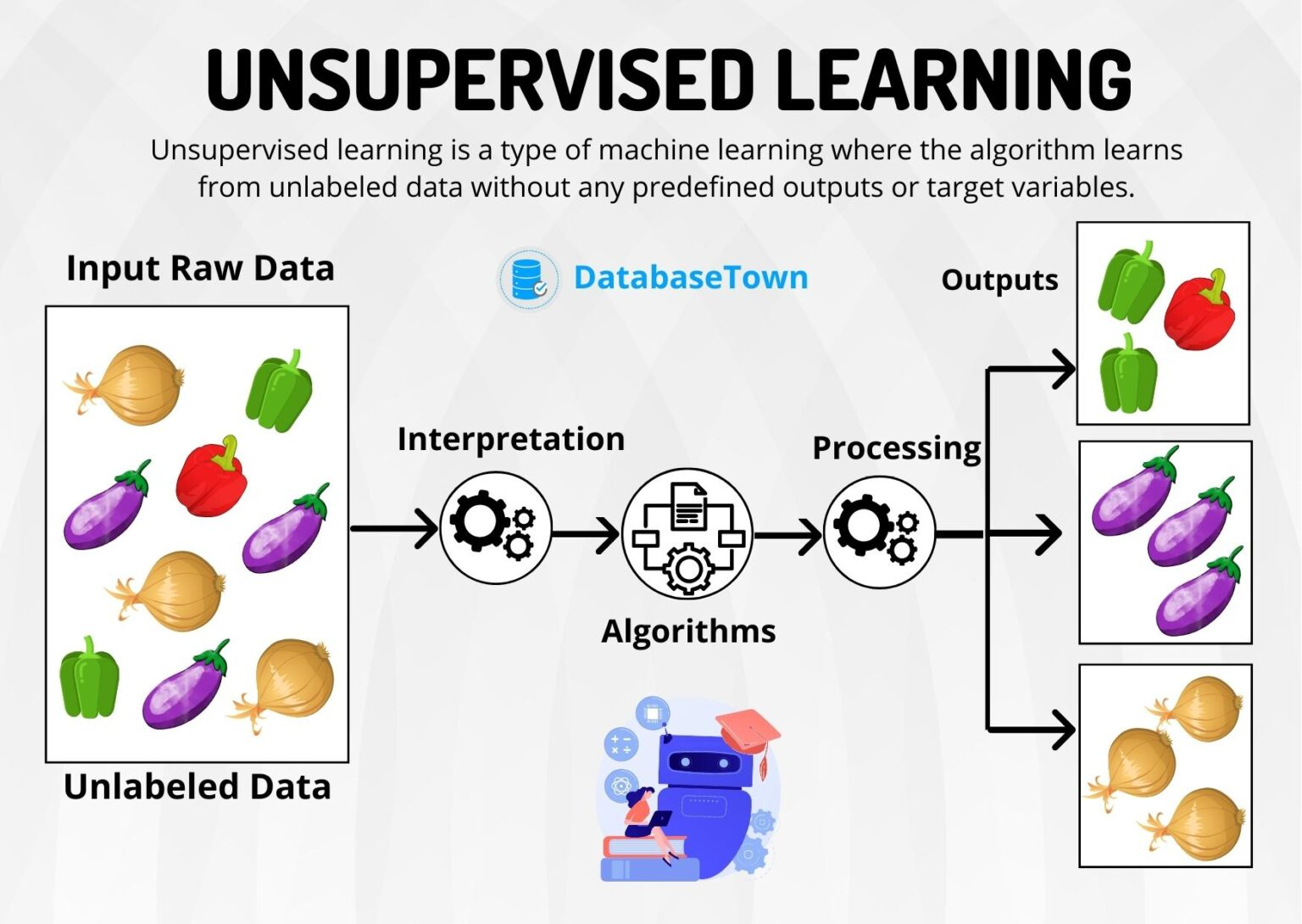
Unsupervised Learning: Types, Applications & Advantages, 출처: https://databasetown.com

1. 군집

라벨 없이 데이터의 자연스러운 그룹을 찾는 작업이다.
목표는 같은 군집 내 유사도 ↑, 군집 간 유사도 ↓이다.

1-1. 군집과 분류의 차이

• 분류: 정답 라벨이 있고, 그 라벨을 예측하는 지도학습이다.
• 군집: 라벨이 없고, 데이터만으로 구조를 발견하는 비지도학습이다. 결과 라벨은 상대적 의미만 가진다.

1-2. 주요 군집 알고리즘

• K-평균(K-Means): 중심(centroid) 기반, 구형(球形) 군집·비슷한 크기에 강함. 빠르고 대용량에 적합.
• 계층적 군집(Agglomerative/Divisive): 병합/분할로 덴드로그램 생성, 거리 연결(linkage: single/complete/average/ward) 기준.
• DBSCAN: 밀도 기반, 임의 모양 군집·노이즈 탐지 강함(매개변수 eps, min_samples).
• Mean Shift: 커널 밀도 최대점으로 수렴, 군집 수 자동 추정(대역폭 민감).
• Spectral Clustering: 그래프 라플라시안 고유벡터로 임베딩 후 K-평균, 복잡 구조에 유리.
• OPTICS/BIRCH: 가변 밀도(OPTICS)·대규모 스트리밍(BIRCH)에서 유용.

1-3. K-평균 vs 계층적 군집

항목	K-평균	계층적(병합)
군집 수	사전 지정 필요(k)	덴드로그램 절단 높이로 선택
형상 가정	구형/비슷한 크기	링크지 선택에 따라 유연
복잡도	O(n·k·iter)	O(n²) 근처(거리행렬), 소규모 적합
장점	빠름·대용량	구조 파악(덴드로그램)·k 미정시 유리
단점	이상치·비구형 취약	큰 데이터 비효율

2. 가우시안 혼합(Gaussian Mixture, GMM)

가우시안 혼합(Gaussian Mixture Model, GMM)은 데이터가 여러 개의 가우시안 분포로 구성된다고 가정하고, 이를 기반으로 군집을 수행하는 비지도 학습 알고리즘이다. 각 데이터 포인트는 특정 가우시안 분포에 속할 확률로 표현된다.

2-1. 학습 단계(EM 알고리즘)

1. 초기화: 혼합비율 πk\pi_kπk, 평균 μk\mu_kμk, 공분산 Σk\Sigma_kΣk
2. E-step: 각 점이 군집 kkk에 속할 책임도 γik=p(z=k∣xi)\gamma_{ik}=p(z=k|x_i)γik=p(z=k∣xi) 계산
3. M-step: πk,μk,Σk\pi_k, \mu_k, \Sigma_kπk,μk,Σk 를 γ\gammaγ로 가중 업데이트
4. 수렴까지 반복, 모델 선택은 BIC/AIC로 군집 수 결정

2-2. 장단점

• 장점: 소프트 클러스터링, 타원형 군집·중첩 데이터에 강함, 밀도 추정·이상치 탐지에 응용.
• 단점: 공분산 형태 선택(Full/Tied/Diag/Spherical)·초기값 민감, 지역 최적·과적합 위험.
  
  
  

3. 실루엣 분석

• 실루엣 계수는 데이터 포인트가 얼마나 잘 군집화되었는지 평가하는 지표다. 실루엣 계수는 다음과 같은 수식으로 정의된다.
  $s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$
  • $a(i)$: $i$번째 데이터 포인트가 속한 군집 내의 다른 포인트들과의 평균 거리
  • $b(i)$: $i$번째 데이터 포인트와 가장 가까운 다른 군집의 포인트들과의 평균 거리

4. DBSCAN 군집화

• 개념: 반경 eps 안에 min_samples 이상 이웃이 있으면 코어 포인트, 연결된 코어/경계 포인트를 군집으로 확장, 나머지는 노이즈로 표시.
• 장점: 임의 모양 군집, 노이즈 강건, k 미지정.
• 단점: 밀도 가변 데이터에서 eps 튜닝 어려움, 스케일링·거리 척도 민감.