딥러닝 numpy로 계산

• 입력을 주고 출력을 관찰하는 것이 추론, 순방향 연산
  

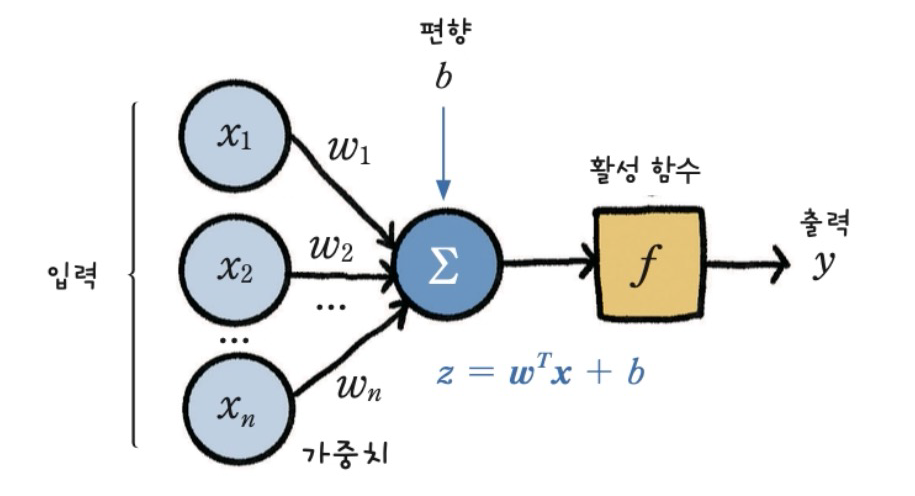
1. raw_weights로 추론

1) 임의의 데이터
2) 가중치를 랜덤하게 선택

• -1 ~ 1 사이의 랜덤한 실수 값을 가지는 1x3 크기의 가중치 배열
  3) 활성화 함수 - sigmoid 함수
  4) 추론 결과

import numpy as np
X = np.array([
    [0, 0, 1],
    [0, 1, 1],
    [1, 0, 1],
    [1, 1, 1],
])

# 2
W = 2 * np.random.random((1, 3)) - 1

# 3
def sigmoid(x):
  return 1.0/(1.0 + np.exp(-x))

# 추론 결과
N = 4
for k in range(N):
    # X의 k번째 행을 전치하여 x에 저장
    x = X[k, :].T
    # 가중치 행렬 W와 x를 행렬곱하여 v에 저장
    v = np.matmul(W, x)
    # 시그모이드 함수를 이용하여 v를 y에 저장
    y = sigmoid(v)
    
    print(y)

2. 가중치 업데이트 하기

1) 지도학습을 위해 정답을 줌
2) 모델의 출력을 계산하는 함수
3) 오차 계산 함수(d 정답, y 추론, e 오차)
4) 한 epoch에 수행되는 W의 계산 함수
5) 가중치를 랜덤하게 초기화하고 학습 시작

# 1
X = np.array([  # features_data
    [0, 0, 1],
    [0, 1, 1],
    [1, 0, 1],
    [1, 1, 1]
])
D = np.array([[0], [0], [1], [1]])  # label_data

# 2
def calc_output(W, x):
  # 입력값과 가중치를 행렬곱하여 v를 계산
  v = np.matmul(W, x)
  # 시그모이드 함수를 이용하여 v를 y로 변환
  y = sigmoid(v)
  return y

# 3
def calc_error(d, y):
  # 실제값 - 예측값
  e = d - y
  # 시그모이드 함수의 미분값 y(1 -y) * 오차 e
  delta = y*(1-y)*e
  return delta

# 4
def delta_GD(W, X, D, alpha):
  for k in range(4): # 4개의 샘플에 대해 반복
    x = X[k, :].T # k번째 샘플의 입력 벡터
    d = D[k] # k번째 샘플의 목표 출력값

    y = calc_output(W,x) # 현재 가중치로 계산한 출력값
    delta = calc_error(d, y) # 오차 계산

    dW = alpha * delta * x # 가중치 변화량 계산
    W = W + dW # 가중치 업데이트

    return W
    
# 5
W = 2*np.random.random((1, 3)) - 1

alpha = 0.9 # learning_rate

for epoch in range(10000):
  W = delta_GD(W, X, D, alpha)
  print(W)
  
# 결과 확인
N = 4

for k in range(N):
  x = X[k,:].T
  v = np.matmul(W, x)
  y = sigmoid(v)
  print(y)

3. XOR

1) 데이터
2) 가중치 랜덤하게 초기화
3) 학습
4) 결과 - 좋지 않다

# 1
X = np.array([ # features_data
    [0, 0, 1],
    [0, 1, 1],
    [1, 0, 1],
    [1, 1, 1]
])
D = np.array([[0], [0], [1], [1]])  # label_data

# 2
W = 2*np.random.random((1, 3)) - 1  # weights

# 3
alpha = 0.9
for epoch in range(10000): 
  W = delta_GD(W, X, D, alpha)

# 4
N = 4 

for k in range(N):
  x = X[k,:].T
  v = np.matmul(W, x)
  y = sigmoid(v)
  print(y)

4. 역전파

• 출력층의 오차 계산 > 출력층 가까이 있는 은닉층의 가중치와 델타 계산 > 다시 그 전 은닉층으로 계산

# output 계산 함수
def calc_output(W1, W2, x):
  v1 = np.matmul(W1, x)
  y1 = sigmoid(v1)
  v = np.matmul(W2, y1)
  y = sigmoid(v)

  return y, y1

# 출력층의 델타 계산
def calc_delta(d, y): 
  e = d - y
  delta = y*(1-y)*e
  return delta

# 은닉층의 델타 계산
def calc_delta1(W2, delta, y1):
  e1 = np.matmul(W2.T, delta)
  delta1 = y1*(1-y1)*e1
  return delta1

# 역전파 코드
def backprop_XOR(W1, W2, X, D, alpha):
  for k in range(4):
    x = X[k, :].T
    d = D[k]

    y, y1 = calc_output(W1, W2, x)
    delta = calc_delta(d, y)
    delta1 = calc_delta1(W2, delta, y1)

    dW1 = (alpha*delta1).reshape(4, 1)*x.reshape(1, 3)
    W1 = W1 + dW1

    dW2 = alpha * delta * y1
    W2 = W2 + dW2

    return W1, W2

# 데이터 준비 & 가중치 랜덤하게 초기화
X = np.array([
    [0, 0, 1],
    [0, 1, 1],
    [1, 0, 1],
    [1, 1, 1]
])
D = np.array([[0], [0], [1], [1]])

W1 = 2*np.random.random((4, 3)) - 1
W2 = 2*np.random.random((1, 4)) - 1

# 학습
alpha = 0.9 
for epoch in range(10000):
  W1, W2 = backprop_XOR(W1, W2, X, D, alpha)
  
# test
N = 4 
for k in range(N):
  x = X[k,:].T
  v1 = np.matmul(W1, x)
  y1 = sigmoid(v1)
  v = np.matmul(W2, y1)
  y = sigmoid(v)
  print(y)

5. Loss함수

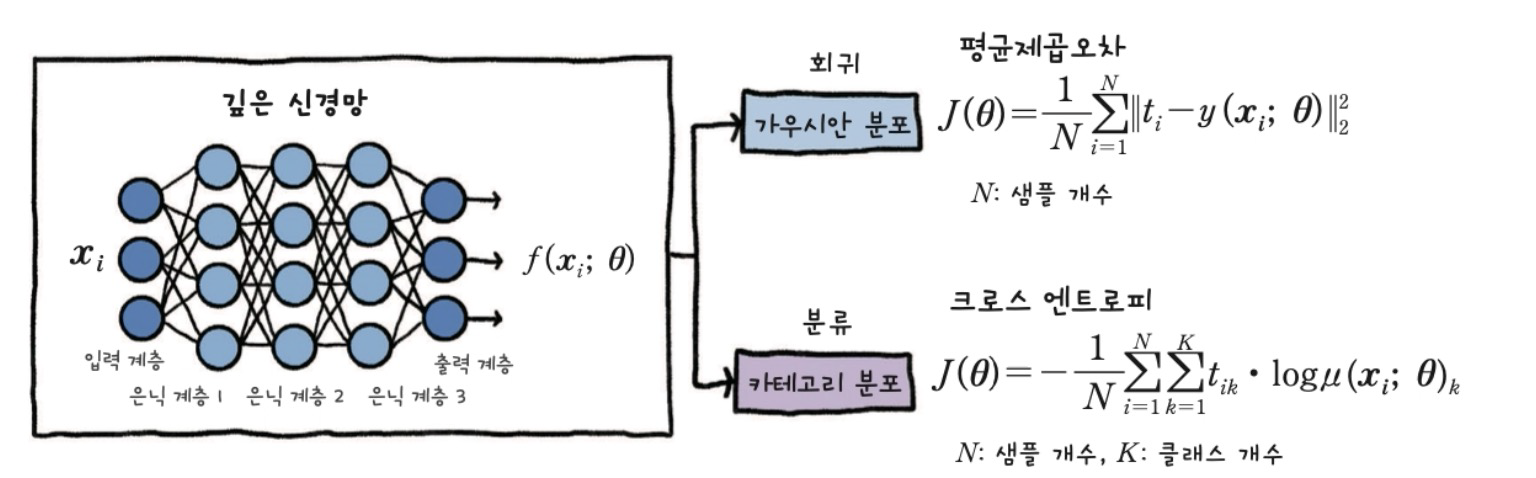
# cross_entropy의 델타
def calcDelta_ce(d,y):
  e = d - y
  delta = e
  return delta

# 은닉층
def calcDelta1_ce(W2, delta, y1):
  e1 = np.matmul(W2.T, delta)
  delta1 = y1 * (1 - y1) * e1
  return delta1

# 역전파
def BackpropCE(W1, W2, X, D, alpha):
  for k in range(4):
    x = X[k, :].T
    d = D[k]

    y, y1 = calc_output(W1, W2, x)
    delta = calcDelta_ce(d, y)
    delta1 = calcDelta1_ce(W2, delta, y1)

    dW1 = (alpha*delta1).reshape(4, 1)*x.reshape(1, 3)
    W1 = W1 + dW1

    dW2 = alpha * delta * y1
    W2 = W2 + dW2

    return W1, W2

# 가중치 초기화
W1 = 2*np.random.random((4, 3)) - 1
W2 = 2*np.random.random((1, 4)) - 1

# 학습
alpha = 0.9
for epoch in range(10000):
  W1, W2 = BackpropCE(W1, W2, X, D, alpha)

# 결과 확인
N = 4 

for k in range(N):
  x = X[k,:].T
  v1 = np.matmul(W1, x)
  y1 = sigmoid(v1)
  v = np.matmul(W2, y1)
  y = sigmoid(v)
  print(y)

6. 예제

1) 데이터 준비 - 숫자 맞추기

import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
%matplotlib inline

# 훈련용 데이터
X = np.zeros((5, 5, 5))
X[:, :, 0] = [[0,1,1,0,0], [0,0,1,0,0], [0,0,1,0,0], [0,0,1,0,0], [0,1,1,1,0]]
X[:, :, 1] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [1,0,0,0,0], [1,1,1,1,1]]
X[:, :, 2] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]
X[:, :, 3] = [[0,0,0,1,0], [0,0,1,1,0], [0,1,0,1,0], [1,1,1,1,1], [0,0,0,1,0]]
X[:, :, 4] = [[1,1,1,1,1], [1,0,0,0,0], [1,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]

D = np.array([[[1, 0, 0, 0, 0]], [[0,1,0,0,0]], [[0,0,1,0,0]], [[0,0,0,1,0]], [[0,0,0,0,1]]])

plt.figure(figsize=(12, 4))
for n in range(5):
    plt.subplot(1, 5, n+1)
    plt.imshow(X[:,:,n])
plt.show()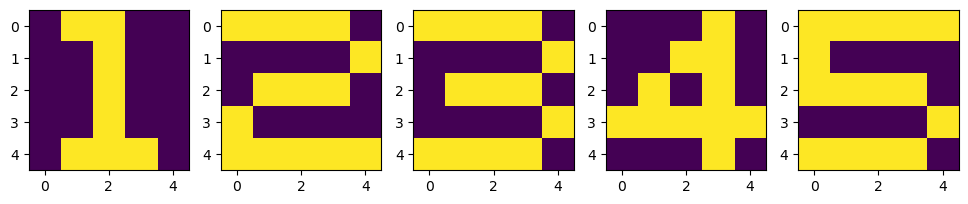

2) 필요 함수

def Softmax(x):
    x = np.subtract(x, np.max(x)) # prevent overflow
    ex = np.exp(x)
    
    return ex/np.sum(ex)
    
# ReLU
def ReLU(x):
    return np.maximum(0, x)

# ReLU를 이용한 정방향 계산
def calcOut_ReLu(W1, W2, W3, W4, x):
    v1 = np.matmul(W1, x)
    y1 = ReLU(v1)
    v2 = np.matmul(W2, y1)
    y2 = ReLU(v2)
    v3 = np.matmul(W3, y2)
    y3 = ReLU(v3)
    v = np.matmul(W4, y3)
    y = Softmax(v)
    
    return y, v1, v2, v3, y1, y2, y3

# 역전파
def backpropagation_ReLU(d, y, W2, W3, W4, v1, v2, v3):
    e = d - y
    delta = e

    e3 = np.matmul(W4.T, delta)
    delta3 = (v3 > 0) * e3

    e2 = np.matmul(W3.T, delta3)
    delta2 = (v2 > 0) * e2

    e1 = np.matmul(W2.T, delta2)
    delta1 = (v1 > 0) * e1

    return delta, delta1, delta2, delta3

# 가중치 계산
def calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4):
    dW4 = alpha * delta * y3.T
    W4 = W4 + dW4

    dW3 = alpha * delta3 * y2.T
    W3 = W3 + dW3

    dW2 = alpha * delta2 * y1.T
    W2 = W2 + dW2

    dW1 = alpha * delta1 * x.T
    W1 = W1 + dW1

    return W1, W2, W3, W4

# 가중치 업데이트
def DeepReLU(W1, W2, W3, W4, X, D, alpha):
    for k in range(5):
        x = np.reshape(X[:,:,k], (25, 1))
        d = D[k, :].T
        
    y, v1, v2, v3, y1, y2, y3 = calcOut_ReLu(W1, W2, W3, W4, x)
    delta, delta1, delta2, delta3 = backpropagation_ReLU(d, y, W2, W3, W4, v1, v2, v3)
    W1, W2, W3, W4 = calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4)

    return W1, W2, W3, W4

#훈련 데이터 검증
def verify_algorithm(x, W1, W2, W3, W4): 
    v1 = np.matmul(W1, x)
    y1 = ReLU(v1)

    v2 = np.matmul(W2, y1)
    y2 = ReLU(v2)

    v3 = np.matmul(W3, y2)
    y3 = ReLU(v3)

    v = np.matmul(W4, y3)
    y = Softmax(v)

    return y

3) 학습

W1 = 2*np.random.random((20, 25))-1
W2 = 2*np.random.random((20, 20))-1
W3 = 2*np.random.random((20, 20))-1
W4 = 2*np.random.random((5, 20))-1

alpha=0.01

for epoch in tqdm(range(10000)):
    W1, W2, W3, W4 = DeepReLU(W1, W2, W3, W4, X, D, alpha)

4) 결과

N = 5

for k in range(N):
    x = np.reshape(X[:,:,k], (25,1))

    y = verify_algorithm(x, W1, W2, W3, W4)

    print('Y = {}'.format(k+1))
    print(np.argmax(y, axis=0)+1)
    print(y)
    print('----------------------')

5) 테스트 데이터

# 테스트 데이터
X_test = np.zeros((5, 5, 5))
X_test[:, :, 0] = [[0,0,0,0,0], [0,1,0,0,0], [1,0,1,0,0], [0,0,1,0,0], [0,1,1,1,0]]
X_test[:, :, 1] = [[1,1,1,1,0], [0,0,0,0,0], [0,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]
X_test[:, :, 2] = [[0,0,0,1,0], [0,0,1,1,0], [0,1,0,0,0], [1,1,1,0,1], [0,0,0,1,0]]
X_test[:, :, 3] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [1,0,0,0,0], [1,1,1,0,0]]
X_test[:, :, 4] = [[0,1,1,1,1], [1,1,0,0,0], [1,1,1,1,0], [0,0,0,1,1], [1,1,1,1,0]]

plt.figure(figsize=(12, 4))
for n in range(5):
    plt.subplot(1, 5, n+1)
    plt.imshow(X_test[:,:,n])
plt.show()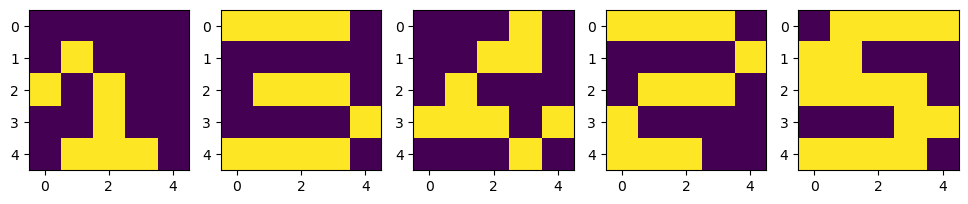

5) 테스트 데이터

learning_results = [0,0,0,0,0]

for k in range(5):
    x = np.reshape(X[:,:,k], (25,1))

    y = verify_algorithm(x, W1, W2, W3, W4)

    learning_results[k] = np.argmax(y, axis=0)+1

    print('Y = {}'.format(k+1))
    print(learning_results[k])
    print(y)
    print('----------------------')

6) dropout 함수 적용

# dropout 함수 생성
def Dropout(y, ratio):
    ym = np.zeros_like(y)

    num = round(y.size*(1-ratio))
    idx = np.random.choice(y.size, num, replace=False)
    ym[idx] = 1.0/(1.0 - ratio)

    return ym

# dropout 적용
def calcOutput_Dropout(W1, W2, W3, W4, x):
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1)
    y1 = y1 * Dropout(y1, 0.2)

    v2 = np.matmul(W2, y1)
    y2 = sigmoid(v2)
    y2 = y2 * Dropout(y2, 0.2)

    v3 = np.matmul(W3, y2)
    y3 = sigmoid(v3)
    y3 = y3 * Dropout(y3, 0.2)

    v = np.matmul(W4, y3)
    y = Softmax(v)

    return y, y1, y2, y3, v1, v2, v3

# 역전파
def backpropagation_Dropout(d, y1, y2, y3, W2, W3, W4, v1, v2, v3):
    e = d - y
    delta = e

    e3 = np.matmul(W4.T, delta)
    delta3 = y3*(1-y3) * e3

    e2 = np.matmul(W3.T, delta3)
    delta2 = y2*(1-y2) * e2

    e1 = np.matmul(W2.T, delta2)
    delta1 = y1*(1-y1) * e1

    return delta, delta1, delta2, delta3

# dropout 적용해서 다시 계산
def DeepDropout(W1, W2, W3, W4, X, D):
    for k in range(5):
        x = np.reshape(X[:,:,k],(25,1))
        d = D[k,:].T

        y, y1, y2, y3, v1, v2, v3 = calcOutput_Dropout(W1, W2, W3, W4, x)
        delta, delta1, delta2, delta3 = backpropagation_Dropout(d, y1, y2, y3, W2, W3, W4, v1, v2, v3)
        W1, W2, W3, W4 = calcWs(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4)
        return W1, W2, W3, W4

7) 학습하고 결과 확인

# 다시 학습
W1 = 2*np.random.random((20, 25))-1
W2 = 2*np.random.random((20, 20))-1
W3 = 2*np.random.random((20, 20))-1
W4 = 2*np.random.random((5, 20))-1


for epoch in tqdm(range(10000)):
    W1, W2, W3, W4 = DeepDropout(W1, W2, W3, W4, X, D)

# 결과 출력
N=5
for k in range(N):
    x = np.reshape(X[:,:,k], (25,1))

    y = verify_algorithm(x, W1, W2, W3, W4)

    learning_results[k] = np.argmax(y, axis=0)+1

    print('Y = {}'.format(k+1))
    print(learning_results[k])
    print(y)
    print('----------------------')

# 결과확인
plt.figure(figsize=(12, 4))
for n in range(N):
    plt.subplot(2, 5, n+1)
    plt.imshow(X_test[:,:,n])
    plt.subplot(2, 5, n+6)
    plt.imshow(X[:,:,learning_results[k][0]-1])
plt.show()

---

Reference
1) 제로베이스 데이터스쿨 강의자료