Heterogeneous Graph (이종 그래프)
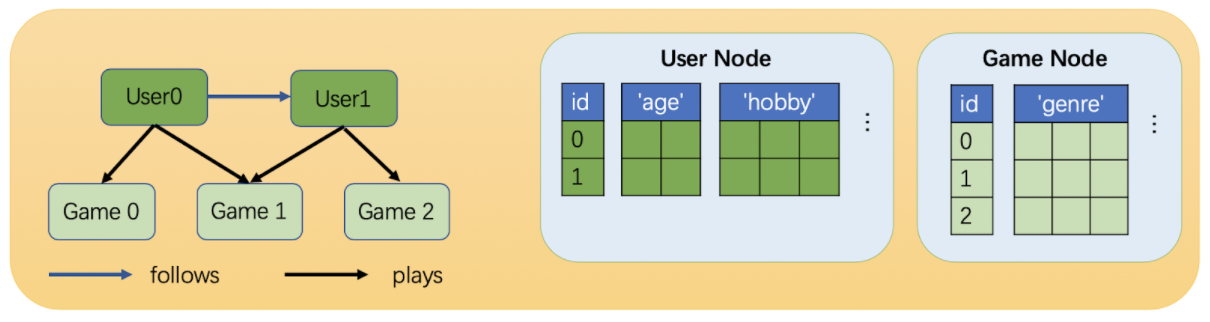
Heterogeneous Graph는 다양한 노드 타입과 엣지 타입을 가지는 그래프를 말한다. 2개의 노드 타입, 2개의 엣지 타입을 가지고 있다고 예시를 들면,
논문, 저자라는 2개의 노드 타입, 인용과 선호라는 2개의 엣지 타입이 있다. 그래프에서 모든 연결은 노드와 노드 사이에 이루어지기 때문에, 총 8가지 관계 타입이 생성된다.
- (논문, 인용, 논문)
- (논문, 선호, 논문)
- (논문, 인용, 저자)
- (논문, 선호, 저자)
- (저자, 인용, 저자)
- (저자, 선호, 저자)
- (저자, 인용, 논문)
- (저자, 선호, 논문)
→ 이렇게 (시작 노드, 엣지, 도착 노드)로 정의할 수 있다. 관계 타입은 노드와 엣지 사이의 상호 작용을 훨씬 잘 설명한다.
- : 그래프 노드 집합
- : 그래프 엣지 집합
- : 노드 매핑 함수 ()
- : 엣지 매핑 함수 ()
- 어떤 노드 타입을 가지는 노드 :
- 노드 v의 노드 타입 :
- 어떤 엣지 타입을 가지는 엣지 :
- 엣지 의 엣지타입 :
- 엣지 e의 관계 타입 :
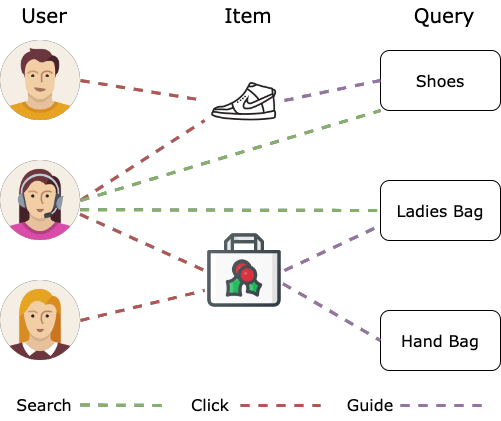
이종 그래프는 위처럼 이커머스 도메인에서도 볼 수 있음. 사용자, 아이템, 쿼리, 위치 등 다양한 노드 타입이 존재하고, 구매, 방문, 검색 등의 다양한 엣지 타입을 가짐.
서로 다른 노드 타입에 따라 다른 피처 공간을 가진다.
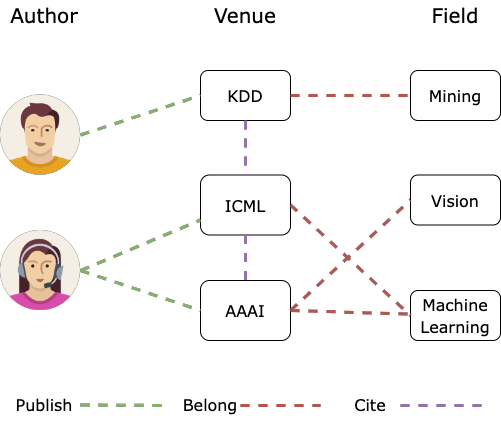
위의 경우도, 저자, 논문, 분야 등의 노드 타입, 출판, 인용 등의 엣지 타입을 가짐.
노드 타입과 엣지 타입은 피처로 사용할 수 있는데, 각 노드 타입과 엣지 타입에 대해 One-Hot Encoding을 수행하면 피처로 만들 수 있다. 그렇게 되면, Hetergeneous graph는 일반 그래프와 똑같아지게 된다.
Heterogeneous Graph가 필요한 경우는 다음과 같다.
- One-Hot Encoding을 효과적으로 수행할 수 없는 상황에 필요하다. 노드마다 갖는 노드 타입이 다르거나, 엣지마다 갖는 엣지 타입이 다른 경우에 필요하다.
→ 예를 들면, 저자 노드는 4개의 피처를, 논문 노드는 5개의 피처를 가지면 One-Hot Encoding을 수행할 수 없다.
- 상호작용에서 서로 다른 관계 타입을 갖는 경우인데, (영어,번역,프랑스어), (영어,번역,중국어)가 예시이다. 이 둘은 서로 다른 모델이 필요하다.
결국, 이종 그래프는 훨씬 표현력이 높은 그래프 표현 방식이다. 엔티티 간의 다양한 유형의 상호 작용을 찾아낼 수 있지만, 계산이나 저장 공간의 관점에서 훨씬 큰 비용을 가지고 구현도 훨씬 복잡하다. 이 문제를 해결하기 위해 이종 그래프를 일반 그래프로 변환하는 방법이 존재한다.
Relational GCN (RGCN)
기본적인 GCN구조는 다음과 같다.
여기서 은 릴레이션 별로 생성된다고 볼 수 있다.
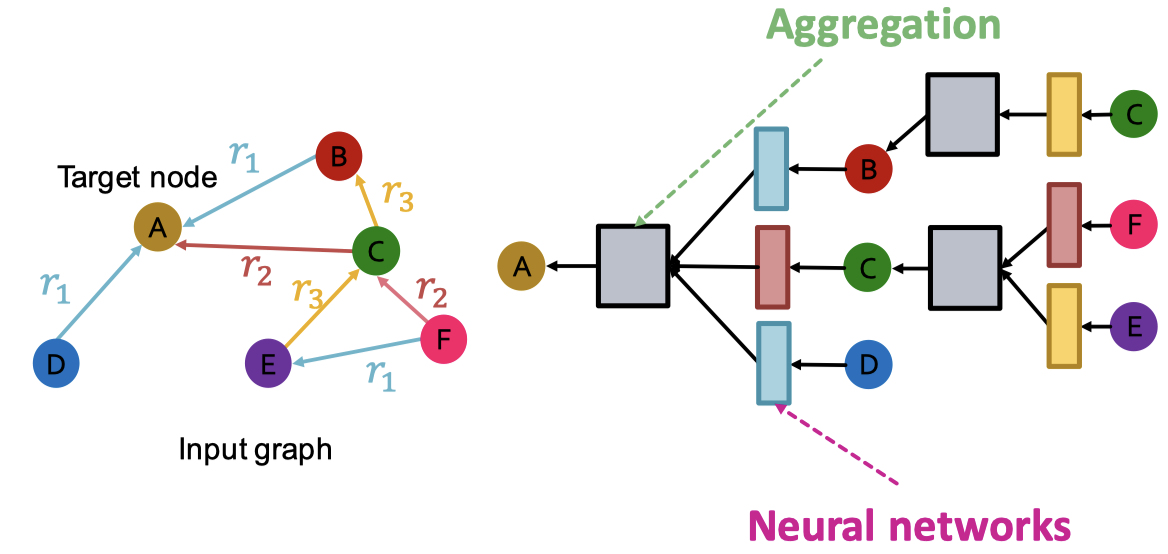
GCN을 다양한 엣지/관계 타입을 가진 이종 그래프를 처리할 수 있도록 확장해야 한다. 우선 하나의 관계를 가진 방향이 있는 그래프로 시작한다.
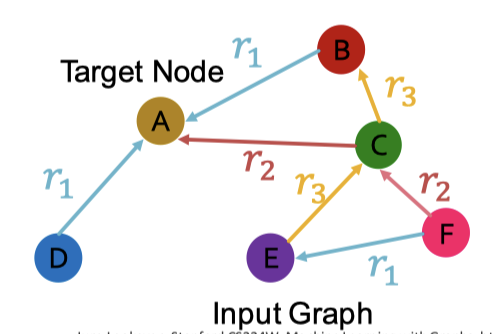
왼쪽의 그래프를 보면, 타겟 노드인 A에 대한 표현은 A방향으로 메시지를 전달하기만 하면 됐다.
오른쪽의 그래프처럼 다양한 관계 타입을 갖는 그래프의 경우는, 서로 다른 뉴럴 네트워크 가중치를 사용한다.
- A → B일 때, weight는
- A → C일 때, weight는
- A → D일 때, weight는
Relational GCN은 다음과 같이 수학적 공식으로 적용한다.
메시지 전달의 경우는 다음과 같다. 우선, 주어진 관계에 대해 각 이웃의 메시지 전달 공식은 다음의 식이다.
자기 자신에 대한 메시지 전달의 식은 다음과 같다.
그리고, 이웃과 자기 자신으로부터 메시지를 모두 더하고 활성화 함수를 적용한다.
위와 같이 설계할 때, 레이어 개수인 개의 행렬 을 계산해야 한다. 그리고 각 의 크기는 로 정의한다.
따라서, 관계가 늘어날수록 계산해야 하는 파라미터의 수가 기하급수적으로 증가한다. 이런 경우, Over-fitting 문제가 발생할 수 있으며,
- Block diagonal matrix
- Basis learning
2가지 방법을 통해 가중치 행렬을 Regularization할 수 있다.
RGCN Regularization
1. Block Diagonal Matrix
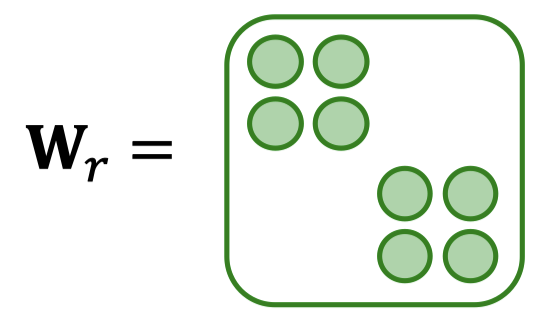
Block diagonal matrix을 통해 가중치 행렬을 보다 희소하게 만드는 것이 목표임. 가중치 행렬을 위 그림처럼 B개의 블록으로 구분 짓게 되면, 파라미터 수는 블록의 개수에 비례해 감소함. 각 차원마다 블록의 개수만큼 연산이 줄고, 블록의 개수만큼 연산하기 때문임.
다음과 같은 수식으로 나타낼 수 있음
2. Basis Learning
다른 관계에 걸쳐 가중치를 공유하는 방식을 말한다. 각 관계의 행렬을 기저 변환의 선형 결합으로 표현하는 것.
개의 기저에 대한 가중치 행렬은 다음과 같이 나타낼 수 있다.
여기서
- 는 기저 행렬
- : 에 대한 가중치
이 경우, 각 관계는 만 학습하면 된다.
위와 같이 그래프가 주어졌을 때, 노드 분류 태스크는 주어진 노드에 대해 레이블을 예측하는 작업을 수행한다. RGCN은 마지막 레이어의 표현을 사용하는데, 만약 개의 클래스에 대해 노드 A의 클래스를 예측한다면, 마지막 레이어에서 가 각 클래스에 대한 확률을 나타낸다.
하지만, Link Prediction이라면, 모든 엣지를 4가지 범주로 먼저 나눈다.
- Training Message Edges
- Training Supervision Edges
- Validation Edge
- Test Edge
위와 같은 그래프에서 를 Training Supervision Edge로 가정하고, 나머지 엣지는 모두 Training Message Edge로 가정한다. 이제는 RGCN을 이용해 에 대한 점수를 매겨야 하는데, 이는 다음의 순서를 따른다.
- E와 A에 대한 최종 임베딩 벡터 를 계산한다.
- 두 벡터를 이용해 관계에 점수를 매길 함수를 정의한다.
- 다음 점수를 계산한다.
학습 과정은 다음과 같다.
-
RGCN을 이용해 Training Supervision Edge 의 점수를 구한다.
-
Training Supervision Edge 에서 도착 노드를 변조해, 와 같은 Negative Edge를 생성한다.
→ 이때, Negative Edge는 실제 그래프에 존재하지 않는 Edge여야 한다.
-
Negative Edge에 대한 점수를 계산한다.
-
Cross Entropy를 이용해 최적화한다.
- Training Supervision Edge에 대한 점수는 최대화, Negative Edge에 대한 점수는 최소화로
- 예시 수식은 다음과 같다.
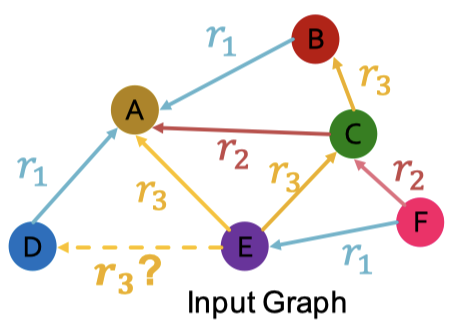
평가시에는, Validation, Test를 동시에 수행, Train Message Edge, Train Supervision Edge를 이용해 Validation Edge를 예측한다. 위 그림처럼 를 예측하는데 이때, 와 같이 Train Message Edge나 Train Supervision Edge에 없는 엣지(Negative Edge)보다 항상 높은 점수가 나오는 것이 좋다. 평가는 다음의 순서를 가진다.
-
의 점수를 계산
-
모든 Negative Edge에 대해 점수를 계산
-
의 순위 RK를 얻는다.
-
다음의 Metric을 계산한다.
- 특정 예측이 상위 k개의 결과 내에 포함되었는지 측정하는 지표
- RK : 대상 예측 결과의 순위
- 특정 예측에 대한 정답의 역순위 계산
- 순위 기반으로 정답이 얼마나 높은 위치에 있는지 세밀히 평가
- 순위가 낮을수록 Reciprocal Rank 값이 높아짐.
Heterogeneous Graph Transformer (HGT)
기존 GNN에 Attention을 활용했던 Graph Attention Network의 식은 다음과 같다.
Attention을 활용했기에, 노드의 이웃이 모두 똑같이 중요한 것이 아니게 됨. 어텐션 가중치인 로 인해 입력 데이터에서 더 중요한 부분에 집중, 나머지에 대해서는 크게 집중하지 않음.
GAT는 아직 그대로 다른 노드 타입과 다른 엣지 타입을 가진 Heterogeneous Graph에 적용할 수는 없다. 각 관계 타입마다 Attention을 적용하기에는, 계산 비용이 너무 커진다.
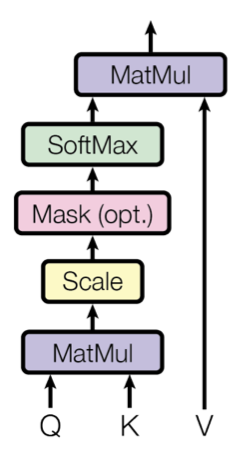
그래서, HGT는 Scaled Dot-Product Attention을 활용한다.
Q, K, V는 각각 쿼리, 키 벡터를 의미하고, 각각은 (Batch size, Dimension)의 크기를 가짐. 또한, 각각은 입력 데이터에 대해 선형 레이어를 태워서 얻을 수 있음.
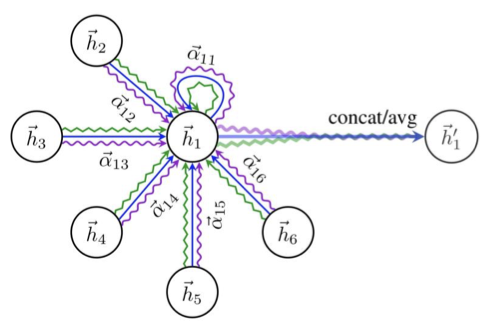
그리고 번째 레이어를 이라고 할 때, 다음과 같다.
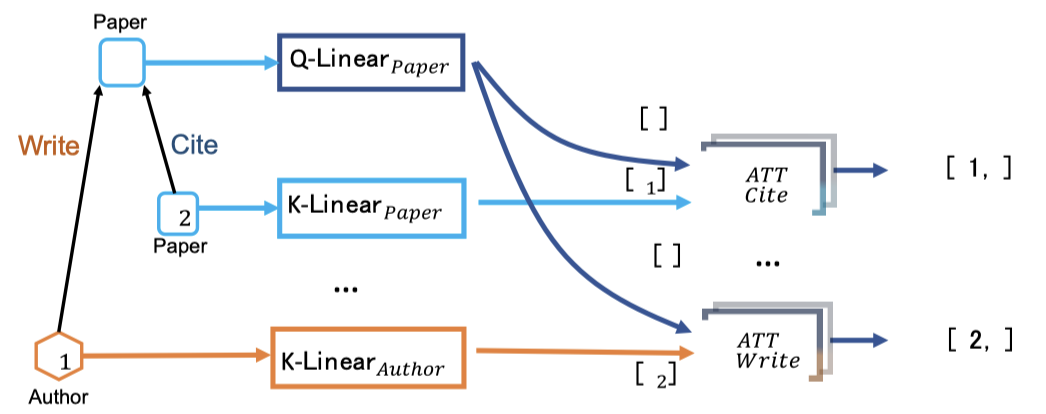
그리고, 노드 타입과 엣지 유형에 종속적인 Attention Machanism을 사용해 이종 그래프의 어텐션으로 분해한다. 3개의 노드 가중치 행렬, 2개의 엣지 가중치 행렬이 있다면, 분해 없이는 모두 18개의 관계 타입에 대한 가중치 행렬이 필요하다. 각각 가중치 행렬을 구분하기 위해서는 Multi-head Attention을 활용해야 할 것 같지만, 같은 피처 분포를 공유하게 되기 때문에, 적절하지 않음. 그렇기에, Heterogenerous Mutual Attention을 활용한다.
여기서 각 관계 는 고유한 가중치 집합을 갖는다.
- : s에 대한 노드 타입
- : e에 대한 엣지 타입
- 는 와 를 파라미터화하는데, 각각은 더 나아가 Key, Query vector인 로 반환된다.
- 엣지 타입 는 를 직접 파라미터화한다.
최종적으로 전체 HGT 레이어는 다음과 같다.
마찬가지로, HGT는 메시지 계산에서 노드 타입과 엣지 타입으로 가중치를 분해한다.
Build Hetergeneous Graph
노드는 여러 종류의 메시지를 받을 수 있고, 메시지의 종류는 관계 타입의 수와 같다. 그렇기에, 각 관계 타입마다 서로 다른 메시지 함수를 만들어줘야 한다.
메시지 계산의 식은 다음과 같다.
에서는 라고 가정한다면, 노드 가 엣지 타입 로 연결되어 있는 노드 로부터 메시지를 받는다.
각 노드는 이웃 노드로부터 여러 종류의 메시지를 수신할 수 있고, 여러 이웃 노드가 각 메시지 종류에 속할 수 있다. 그렇기에, Aggregation의 경우, 두 단계의 메시지 전달을 정의해 집계한다.
노드로 전송된 모든 메시지가 주어질 때, 각 메시지 유형 내에서 엣지 타입에 속하는 메시지를 로 집계한다. 그리고 모든 엣지 타입에 대해 로 모두 집계한다.
그리고, 이종 그래프에 대해 전처리 layer, 후처리 layer을 둘 수 있는데, 각 노드 타입에 대한 MLP 레이어가 됨.
추가로, GNN 디자인 시 Skip Connection, Batch Normalization 등도 활용가능하다.
기존 GNN에서는 그래프 피처나 그래프 구조에 대한 조작을 가해 성능을 향상했다. 이종 그래프에서도 비슷하게 조작이 가능한데, Feature 관점에서 2가지가 존재한다
- 각 Relation Type마다 node degree와 같은 그래프 통계값을 계산하기
- 관계 타입을 무시하고 전체 그래프에 대해 통계값을 계산하기
그래프 구조에서는 기존과 같이 이웃 샘플링과 서브그래프 샘플링을 사용할 수 있다. 다만 각 관계 타입마다 샘플링을 할지, 전체 그래프에 대해 샘플링을 할지 정해야 한다.
이종그래프의 예측 헤드는 레벨별로 다음과 같다.
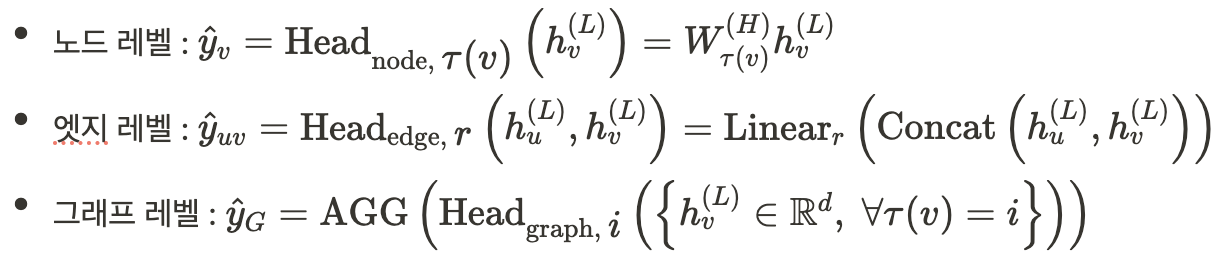
참조
https://otzslayer.github.io/cs224w/2023/06/30/cs224w-09.html
https://velog.io/@stapers/Lecture-10-Heterogeneous-Graphs-and-Knowledge-Graph-Embeddings
