[CS224W] Lecture 10 - Heterogeneous Graphs and Knowledge Graph Embeddings

김재희·2021년 9월 23일

CS224W GNN

CS224W

목록 보기

10/11

0. Intro

이전까지 우리가 다뤄왔던 그래프는 모두 한 종류의 엣지와 노드를 가진 그래프였다. 하지만 다양한 종류의 엣지와 노드를 가진 그래프가 존재한다. 이번엔 이러한 그래프를 다루는 방법에 대해 배워보도록 하자.

우선 heterogenous graphs에 대해 정의해보자. heterogeneous graph는 다음과 같은 요소로 이루어져 있다.

G = (V, E, R, T)

노드 : $v_i \in V$
각 연결 종류에 따른 엣지 : $(v_i, r, v_j) \in E$
노드 종류 : $T(v_i)$
연결종류 : $r \in R$

여기서, 엣지는 두 노드 사이에 어떤 연결 종류를 가지는 지에 따라 결정되고, 노드 종류는 이를 결정하는 함수에 각 노드가 입력되어 결정된다는 점을 명심하자.

heterogeneous graph의 예시로는 다음과 같은 그래프들이 있다.

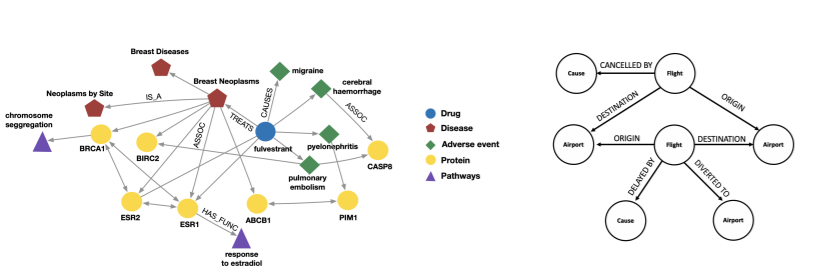
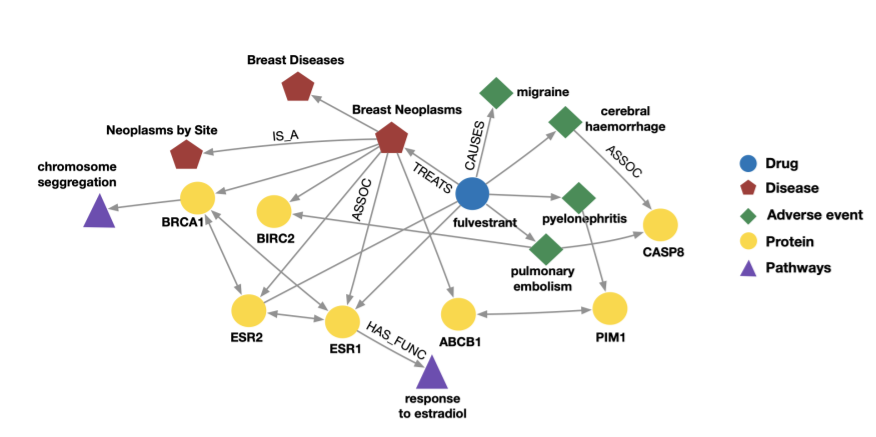
왼쪽 그래프는 약품, 질병, 단백질 등의 노드를 가지면서, 치료, 유발, 효과 등의 엣지를 가지는 그래프이며, 오른쪽은 공항, 비행, 경로 등의 노드를 가지면서 연착, 출발, 목적지 등의 엣지를 가지는 그래프이다. 즉, 복잡한 관계를 보이는 그래프는 이와 같이 다양한 종류의 노드와 엣지를 이요해 표현할 수 있다는 것을 알 수 있다.

1. Relational GCN

1-1. directed graph

그러면 어떻게 GNN이 heterogeneous graph를 다룰 수 있는지 보자. 우선 간단한 그래프 구조부터 생각하자.

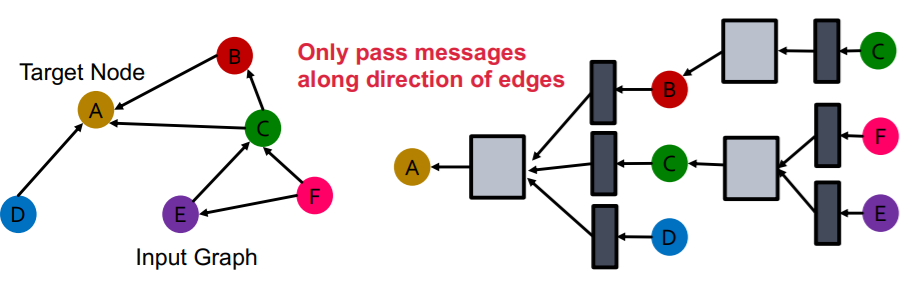
위 그림처럼 노드와 엣지의 종류는 한가지이지만, 방항성이 있는 directed graph에서 GCN은 어떻게 동작할 수 있을까? 간단하다. 그냥 계산 그래프를 방향성에 맞게 만들어주면 된다. 즉, 위 그래프에서 B는 A와 C와 연결되어 있지만, 메세지가 C에서 와서 A로 전달되는 구조이므로, 계산 그래프도 이에 상응하도록 작성하면 된다. 즉, 인접행렬이 비대칭으로 작성되므로 그냥 이를 이용하면 된다.

여기서 GCN에 대해 잠깐 복습을 하자. 자세한 내용은 이전 수업에서 다뤘으므로 생략하겠다.

GCN 레이어 하나의 기본적인 식은 위와 같다. 각 레이어마다 개별적인 weight matrix를 가지며, 각 레이어마다 모든 노드가 각자의 임베딩 벡터를 가진다. 레이어를 통과한다는 것은 이웃노드와 본인노드의 이전 레이어의 임베딩를 더하고, 선형변환을 가한뒤, 비선형성을 추가해주는 것을 의미한다.

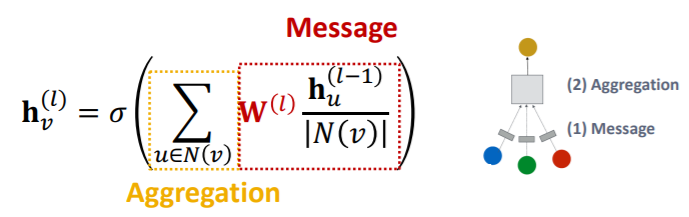
이를 message passing으로 생각하면 위처럼 조금 식을 변형할 수 있다. 즉, 이웃 노드와 자신 노드의 이전 레이어의 임베딩 벡터는 선형변환을 통해 message transformation이 일어나고, 이를 summation 함수를 통해 합쳐지게 된다. 이때, 임베딩 벡터의 크기는 유지하기 위해 이웃노드의 수로 normalization해준다.

1-1. multiple relation type

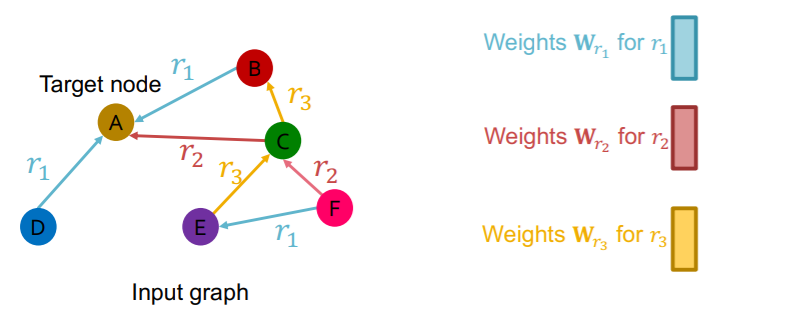
그러면 위의 그림처럼 노드의 종류는 하나이지만, 다양한 관계의 엣지가 있는 그래프에선 어떻게 할까?

간단하다. 각 관계마다 다른 weight matrix를 가지면 된다. 즉, 어차피 기존의 GCN에서도 엣지를 통한 message passing은 weight matrix를 통해 표현되었기 때문에, 다른 관계의 엣지는 다른 weight matrix를 가지게 된다.

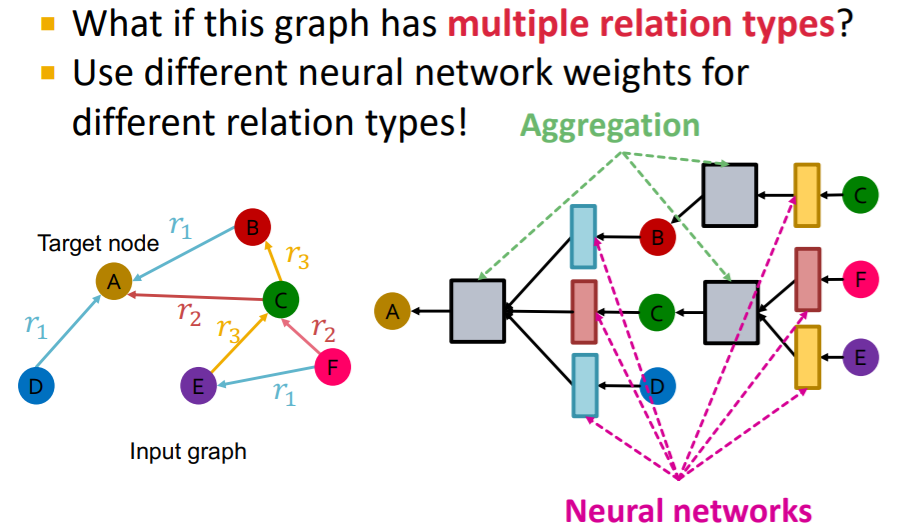
이를 계산 그래프로 표현하면 위와 같다. 복잡해보이지만 단순하다. GCN의 aggregation function은 단순 element wise mean이므로 파라미터가 없어 관계마다 달라질 필요는 없다. message translation에 있는 weight matrix만 각 관계마다 새로이 가지도록 계산그래프를 구성하면 된다.

좀더 자세히 수식을 통해 Relational GCN(RGCN)을 살펴보자.

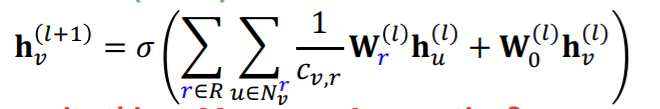
이전 GCN 식과 달라진 부분은 summation 함수가 두개라는 점인데, 이유는 각 관계마다 또 summation이 이루어져야 하기 때문이다. 이로인해 weight matrix는 각 관계마다, 레이어마다 가지게 된다.

message transformation

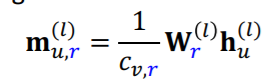
message는 동일한 관계를 가지는 이웃노드의 이전 레이어의 임베딩 벡터의 선형변환을 통해 표현된다. 이때, 그 관계를 가지는 이웃노드의 수로 normalizing이 이루어진다.

자기 자신의 임베딩 벡터 역시 이에 상응하는 해당 레이어의 weight matrix와의 연산을 통해 message가 된다.

aggregation

aggregation은 일반적인 GCN과 동일하다. 다만, 각 관계마다 이웃노드의 수가 달라지므로, 명시적으로 element wise mean이 보이지 않을따름이다.

1-2. Scalability

RGCN은 여러 관계를 가지는 그래프에 대한 모델링이 가능하지만 한가지 문제점이 있다. 파라미터 수가 너무 많아 쉽게 과적합이 발생할 수 있다는 점이다. 위에서 언급했다싶이 RGCN은 매 레이어마다, 매 관계마다 다른 weight matrix를 가진다.
L계의 hidden layer를 가지는 RGCN은 각 관계마다 다음과 같은 weight matrix를 가진다.

W^1_r, W^2_r, \dots, W^L_r

또한, 하나의 weight matrix는 $d^{l+1} \times d^l$ 개의 파라미터가 있다. 그런데 그래프에서 관계의 수는 수백가지에 이르기도 한다. 이는 기존의 GCN에 비해 RGCN이 수백배 많은 파라미터 수를 가질 수도 있다는 것을 의미한다.

과적합을 해소하기 위해 대표적으로 block diagonal marix와 basis learning 두가지 방법이 사용된다고 한다.

Block Diagonal Matrix
하나의 행렬에 대해 대각방향으로만 부분행렬이 존재하도록 만드는 것을 block diagonalization이라 한다. 가중치 행렬을 blcok diagonal matrix로 만들면, 대각방향의 부분행렬에만 원소가 존재하고, 나머지 부분은 0이 되므로 sparse matrix가 되어 훨씬 파라미터의 수가 줄어들게 된다.

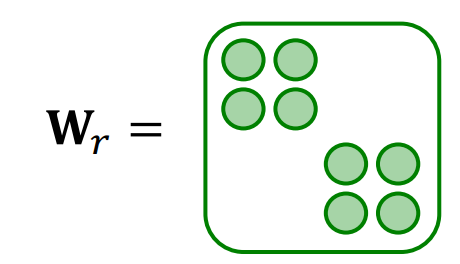
그래서 위와 같은 형태로 weight matrix를 구성하는 것을 block diagonal matrix라 하는데, 이는 DNN 구조로 본다면, 근처에 있는 노드에 대해서만 연결되어 있는 모습이 된다.

위의 그림은 DNN 압축에 관한 논문인 MPDCompress에서 가져온 그림인데, c 그림이 block diagonal matrix일 경우의 그림이 된다. 즉 위와 같이 근처 노드에 대해서만 가중치가 부여되는 모양이 된다. 이 경우 파라미터의 수가 $d^{l+1} \times d^l$ 에서 $B \times {d^{l+1}\over B} \times {d^l \over B}$ 로 훨씬 줄어들게 된다.
하지만 근처 노드끼리만 연결되어 모든 임베딩 벡터 내 원소들 간의 관계에 대해 파악하지 못하게 되는 단점이 존재하게 된다.

Basis Learning
basis learning은 다른 관계의 파라미터를 공유하도록 하는 것이다. 모든 관계의 weight matrix의 basis에 해당하는 행렬들을 만들고 이 basis의 선형 결합으로 각 관계의 weight matrix를 표현하고자 한 것이다.

수식으로 보자면, basis에 해당하는 행렬을 $V_b$ 라 한다. basis는 B개가 존재한다. 그리고 한 관계의 weight matrix는 다음과 같이 표현된다.

W_r = \sum^B_{b = 1} a_{rb} \cdot V_b

이때 $a$ 는 선형결합의 계수로 학습되는 스칼라값이다.

1-3. Examples

그래프 학습, 평가 및 추론에 대한 자세한 내용은 이전 수업에서 다룬 바 있다. 자세한 내용은 해당 챕터를 참고하자.
Node Classification

노드 분류는 분류하고자 하는 노드의 임베딩 벡터만 있으면 되기 때문에 비교적 간단하다. 그냥 해당 노드의 최종 임베딩 벡터를 받아 다운스트림 태스크에 적합한 모델을 붙이면 된다.

Link Prediction

링크 예측의 경우 데이터 구성부터 신경써야 한다. 수백개의 관계가 있다면 각 관계마다 데이터 수가 적을 수도 있고, 관계를 고려하지 않고 랜덤 샘플링하면 특정 관계는 validation이나 test에 없을 여지가 있다. 이때문에 층화학습을 통해 모든 관계가 가급적 비슷한 분포를 가지고 training, validation, test에 있도록 해야한다.

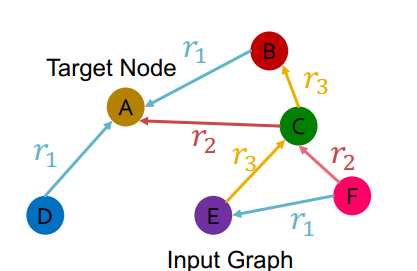
기본을 짚고 넘어가면 위와 같은 그래프에서 $(E, r_3, A)$ 링크에 대한 점수를 얻기 위해서는 다음과 같은 작업이 수행되어야 한다.

$h_E^L, h_A^L \in \mathbb{R}^d$ : E와 A의 임베딩 벡터를 얻는다.
$f_r : \mathbb{R}^d \times \mathbb{R}^d \to \mathbb{R}$ : 두 벡터에 대해 점수를 구할 함수를 정의한다.
$f_{r_1}(h_E, h_A)$ : 점수를 구한다.

이때 각 관계에 속할 점수를 구해야 하기 때문에, 2번의 점수를 구할 함수는 각 관계마다 또 만들어야 한다. 예를 들어 $f_{r_1}(h_E, h_A) = h^T_EW_{r_1}h_A(W_{r_1} \in \mathbb{R}^{d \times d})$ 로 되어 있다면, 여기서 해당 함수의 파라미터인 $W_{r_1}$ 가 있으므로, 각 관계마다 새로 $f_r$ 을 만들어야 한다.

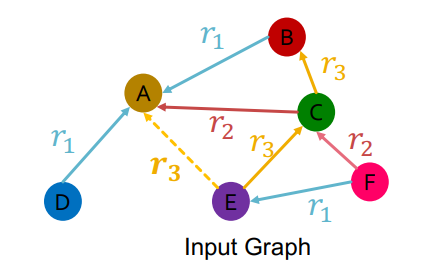
학습 과정은 다음과 같이 이루어진다.

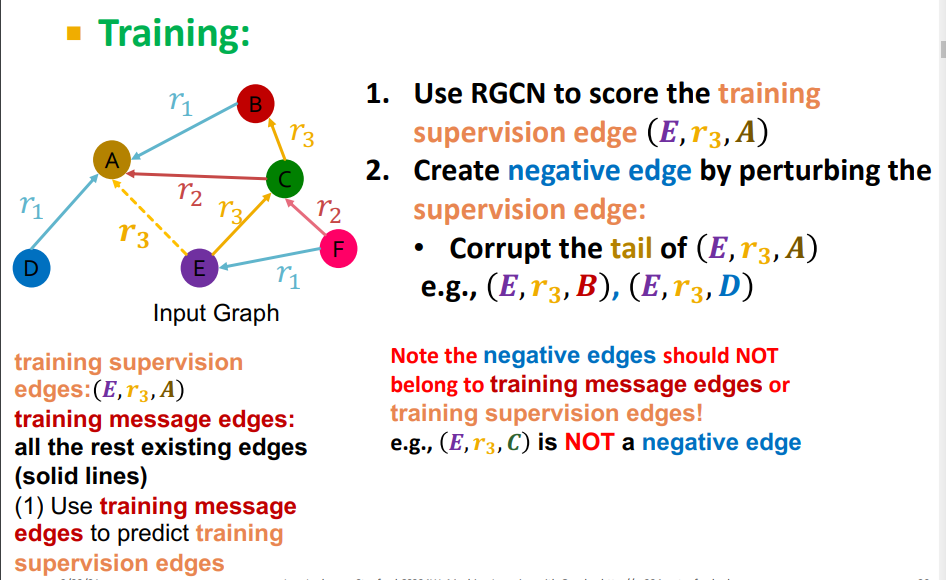
training supervision edge : $(E, r_3, A)$
training message edge : 나머지 엣지
negative edge : supervision edge에 포함되지 않는 나머지 조합, $(E, r_3, A)$ 등등.
이때, negative edge는 training supervision 이나 message edge가 아니어야 한다. 주로 뒷 부분의 노드를 변경하여 구한다.

RGCN을 통해 구한 임베딩 벡터를 통해 supervision edge의 스코어를 구한다.
$f_{r_3}(h_E, h_E)$
RGCN을 통해 구한 임베딩 벡터를 통해 negative edge에 대해 스코어를 구한다.
$f_{r_3}(h_E, h_A)$
Cross Entropy loss를 이용해 최적화한다. 이를 통해 training supervision edge에 대한 score를 최대화하고, negative edge에 대한 score를 최소화한다.

평가 과정은 다음과 같다.

validation edge : $(E, r_3, D)$

RGCN을 통해 구한 임베딩 벡터로 validation edge에 대해 스코어를 구한다.
RGCN을 통해 구한 임베딩 벡터로 모든 negative edge에 대한 스코어를 구한다. 이때, negative edge는 training message edge와 training supervision edge가 아닌 조합이다.
1과 2에서 구한 스코어를 기준으로 랭킹을 매긴다.
hit@k나 reciprocal rank를 목적함수로 사용한다.

이때 4번에서 이렇게 hit@k나 reciprocal rank를 사용해서 validation edge의 스코어를 최대화하려는 이유는 무엇일까? 이는 실제로 존재하는 엣지라면 당연히 존재하지 않는 가상의 엣지인 negative edge에 비해 점수가 높을 것이다. 점수가 높다면 랭킹도 높을 것이다. 이를 해당 목적함수를 이용해 맞추게 된다. 이때, 왜 크로스 엔트로피를 이용하지 않고 추천시스템 등에서 주로 사용하는 목적함수를 사용하는지는 궁금하다...

2. Knowledge Graph

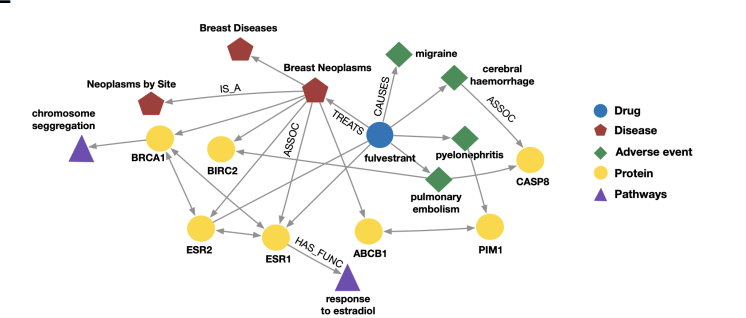
지식 그래프는 지식을 요소, 관계 그리고 그 종류를 이용해 그래프의 형태로 표현한 것이다. 예를 들어, 위와 같이 약, 질병, 단백질과 경로 등에 대한 그래프가 있다면, 노드들의 종류와 노드 간에 어떠한 관계를 가지는지 다양한 종류의 엣지를 통해서 표현할 수 있다. 이때 위의 그래프는 이미 관련 도메인에서 수집되고 정리된 정보를 heterogeneous graph의 형태로 표현했기 때문에 특별히 지식 그래프라 부른다.

실제로 IBM의 왓슨이나 구글의 검색에 사용되는 구글 지식 그래프, 아마존 상품 검색에 이용되는 아마존 상품 그래프 등 상업적으로 다양한 회사에서 자체적으로 구축한 지식그래프가 사용된다.
위와 같이 구글에 특정 키워드를 검색하면 해당 키워드와 관련된 정보들이 정리된 형태로 표현되는데, 이는 넷플릭스라는 노드와 연결된 수많은 노드를 정리한 것이다. 이러한 정보들은 모두 지식 그래프의 형태로 저장된다.

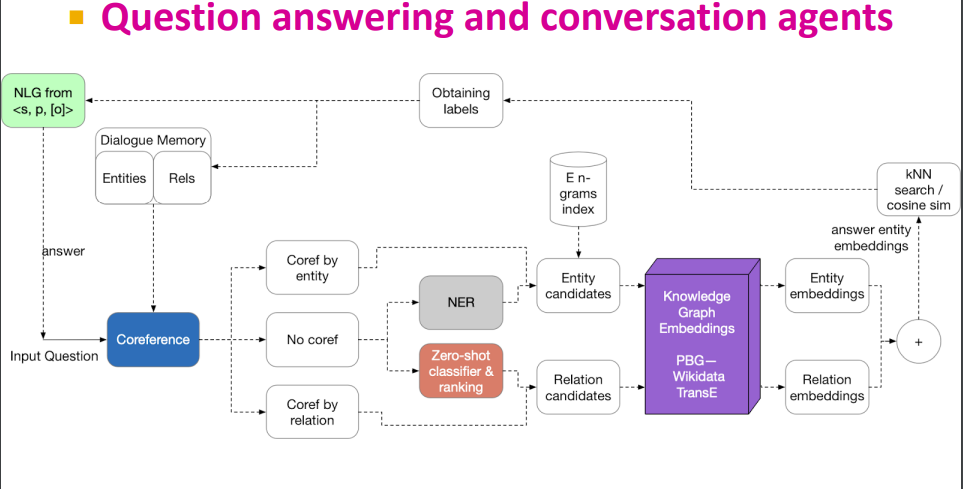
NLP와 연관지어 보자면 QA가 지식 그래프와 깊은 관련이 있다. 시리나 빅스비에 대한민국의 건국연도는? 과 같은 질문을 하면 관련된 정보를 검색하여 찾아주는데, 이때 위키피디아나 자체 구축 지식 그래프 등에서 정보를 찾게 된다.

즉, 그냥 구축된 정보에 대한 관계망을 구축한 것을 지식그래프라고 한다. 여기서 구축된 정보를 모두 그래프에 넣다보니 문제가 생긴다. 어쩔수 없이 구축된 DB는 불완전 할 수 밖에 없다. 페이스북의 이용자들 대다수는 자신의 개인정보를 모두 입력하지 않고, 이는 해당 유저 노드가 출생연도, 출신학교, 거주지역 등의 중요한 노드와 연결되지 않은 상태를 의미한다. 결국 지식그래프에서 관건은 거대한 지식 그래프에서 가능성이 높은 엣지를 찾아내느냐에 달려 있다. 이를 Knowledge Graph Completion이라 한다.

2-1 KG Completion Task

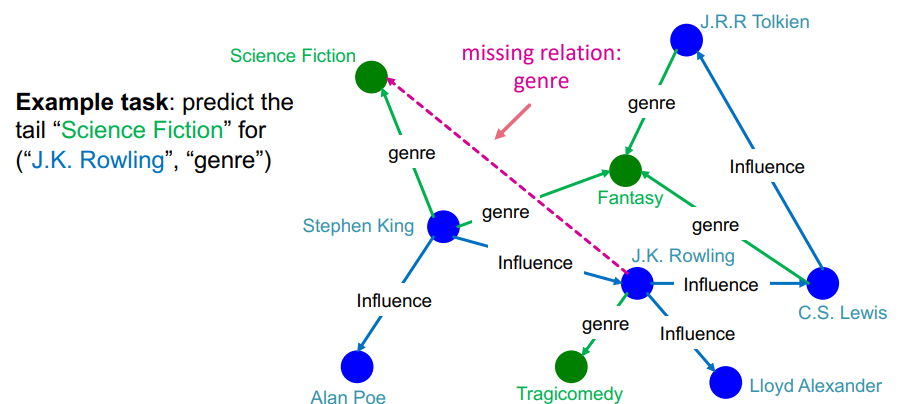
completion task를 link prediction과 비슷하다고 여길 수 있지만, 실제로는 그렇지 않다고 한다. link prediction은 노드 두개가 주어진 상황에서 엣지가 존재할 확률을 계산하는 태스크라면, completion task는 노드 하나와 엣지가 주어진 상태에서 부합하는 노드를 예측하는 태스크이기 때문이다. 예를 들어 위의 그림과 같은 지식 그래프가 주어진 상태에서 J.K.Rowling이라는 노드의 장르라는 관계로 연결되어 있는 노드를 찾는 것이 completion task이다. 정리하자면 다음과 같다.

link perdiction의 input과 output : (node A, node B)과 연결 확률
completion task의 input과 output : (head, relation)과 tail

물론 노드나 엣지의 임베딩 벡터는 gnn으로 구할 수 있지만, 설명의 용이성을 위해 앞으론 룩업테이블을 이용해 임베딩했다고 생각하자.

2-2. Connectivity Patterns

completion task를 수행하는 방법들을 살펴보기에 앞서 지식 그래프에서 다루는 관계의 종류에 대해 짚고 넘어가자. 여기서 관계의 종류는 heterogeneous graph에서 이야기하는 종류가 아니라 하나의 관계가 가질 수 있는 성질에 대한 이야기다. 예를 들어 roommate라는 관계는 대칭적이다. 즉, (a, rommate) = b가 성립한다면, (b, roommate) = a도 성립한다. 이와 같이 관계들은 몇가지 성질을 가지고 있다.

Symmetric relations

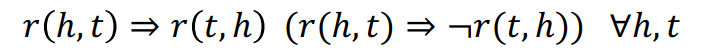
위에서 이야기했듯이, head와 tail이 바뀌어도 동일한 관계가 성립되는 경우다. 대표적인 예시로는 가족여부, 룸메이트 여부 등이 있을 것이다.
Antisymmetric relations
반대칭관계라 번역하는 이 관계는 1번의 대칭관계와 다른 개념이다. 반대칭 관계는 쉽게 말해 (h, r) = t일때, (t, r) != h인 관계를 의미한다. 예를 들어 부모와 자식의 관계가 이에 해당한다.
Inverse relations

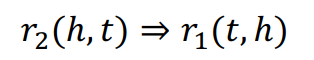
symmetric relation과 반대로 head와 tail이 바뀌면 다른 관계가 성립되는 경우다. 교수-학생의 관계가 성립할 것이다.
Composition relations

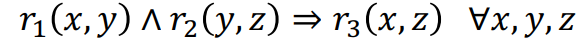
논리학에서 이야기하는 3단논법으로 설명되는 관계이다. 즉, 각기 다른 두 관계에 의해 정의된 세 요소가 3번째 관계로 정의되는 경우이다. 예를 들어, (Jaehee, go) -> starbucks, (starbucks, sell) -> coffee라면 (Jaehee, buy) -> coffee가 성립할 수 있을 것이다(물론 이것보다 엄격한 관계이다.).
1-to-N relations

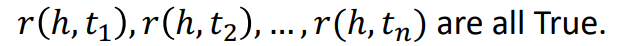
하나의 head가 하나의 relation에 대해 여러 tail을 가질 때 성립한다. 예를 들어 StudentsOf라는 교수가 가진 학생을 의미하는 관계가 가능할 것이다.

3. TransE

이제 하나씩 KG completion을 다루는 방법론을 살펴보고, 해당 방법론들이 위의 관계의 성질 중 몇개를 유지할 수 있는지 알아보자. 가장 처음에 볼 것은 가장 직관적인 TransE이다. TransE의 원리는 다음과 같다.

$(h, r, t), h, r, t\in \mathbb{R}^d$ 가 있다고 하자. 이때, TransE는 실제로 세 요소가 가능한 조합이라면 $h + r \approx t$ 가 성립하도록 만들고자 한다. 즉, $h + r - t = 0$ 이 되도록 하는 것을 목표로 한다. 이로 인해 scoring function은 다음과 같다.

f_r(h, t) = -||h +r-t||

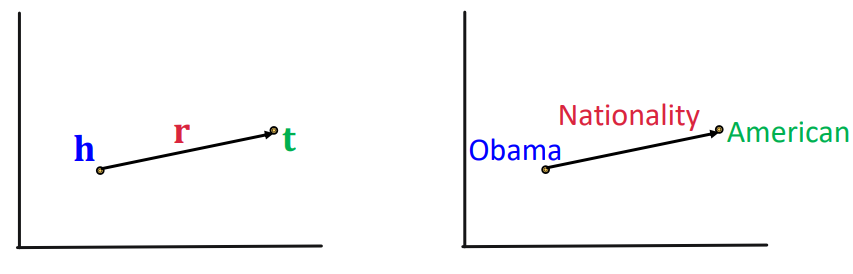
TransE의 개념은 단어 임베딩에서 자주 나오는 개념이다. 즉, 임베딩이 옳바로 되었다면 두 단어의 관계는 항상 일정한 벡터로 표현된다는 이야기다. 예를 들어 king - man + woman = queen과 같이 말이다. 그러므로 위의 그림에서 다른 head와 tail을 가져오더라도 nationality는 동일하게 가르키게 된다. 즉, Jaehee + Nationality = Korea가 될 것이다.

전반적인 학습 알고리즘은 다음과 같다.

모든 노드를 동일한 벡터로 초기화한다. 모든 관계 역시 동일한 벡터로 초기화 한다.
노드 벡터를 단위벡터화한다.
학습에 사용할 (h, l, t)를 선택한다.
학습에 사용할 (h, l, t')를 선택한다. 이때, t'는 해당 관계가 성립하지 않는 노드이다.
임베딩 벡터를 다음 목적함수를 최소화하도록 최적화한다. $\sum_{((h, l, t), (h, l, t')) \in T_{batch}} \nabla [\gamma +distance(h + l, t) - distance(h+ l, t')]$ 즉, 실제 관계가 성립하는 요소들에 대해서는 거리를 최소화하고, 관계가 성립하지 요소에 대해서는 거리를 최대화한다. Word2Vec의 식과 매우 유사하다.

3-1. 성질

TransE는 벡터공간의 기본연산을 이용했기 때문에, 비교적 직관적으로 성질을 보일 수 있다.
Antisymmetric

반대칭관계는 성립한다. 위 그림에서 보이는 것처럼 $t = h +r$ 이라 해서 $h = t+r$ 이 성립하지 않기 때문이다.

Inverse

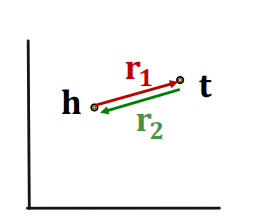
inverse관계는 성립한다. 벡터공간에서 마이너스 부호를 붙여 방향을 뒤집을 수 있기 때문이다. 즉, $h + r = t$ 이며 $t -r =h$ 이다.

Composition

composition 역시 가능하다. 관계도 벡터로 취급하기 때문에 가능한데, 위와 같은 상황에서 $y = x + r_1, z = y + r_2$ 이므로, $z = x+ r_1 + r_2$ 가 되기 때문이다.

Symmetric

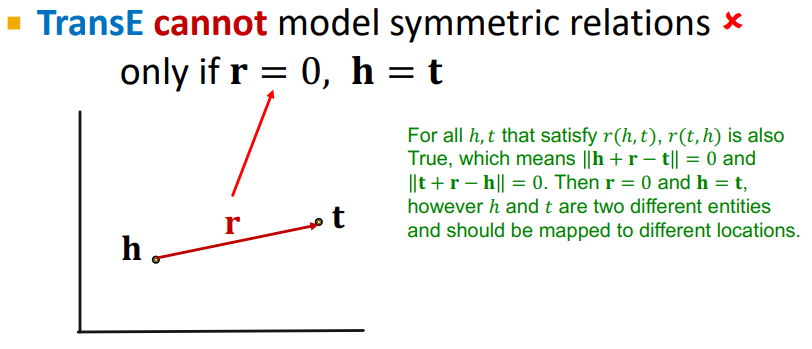
대칭 관계는 당연히 성립하지 않는다. 대칭 관계가 성립하면 $h + r = t, t+ r =h$ 여야 하는데 이 경우가 참일 때는 $h = t$ 여야 하는데, 이는 두 노드가 동일 노드라는 이야기가 되기 때문이다.

1-to-N

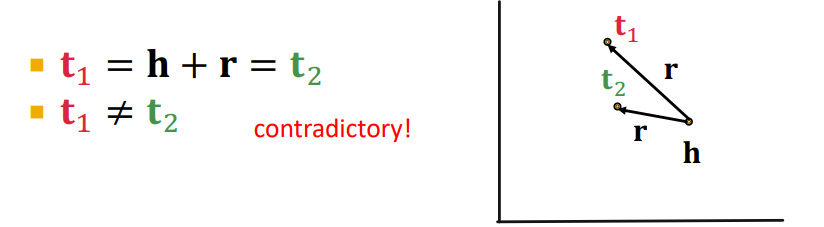
1-to-N 역시 성립하지 않는다. 관계를 벡터로 취급하기 때문에 위 그림과 같이 $(h, r)$ 은 $h$ 에 대한 단사함수이다.

4. TransR

TransR은 TransE가 가진 문제를 entity 공간과 relation 공간을 분리하여 해결한다. 즉, entity 는 $h, t \in \mathbb{R}^d$ 로, relation은 $r \in \mathbb{R}^k$ 로 두고, entity 공간을 relation 공간으로 맵핑하는 선형변환 $M_r \in \mathbb{R}^{k \times k}$ 를 만든다. 이때, 각 relation마다 다른 공간을 형성하기 때문에, 공간마다 새로이 선형변환을 가지게 된다.

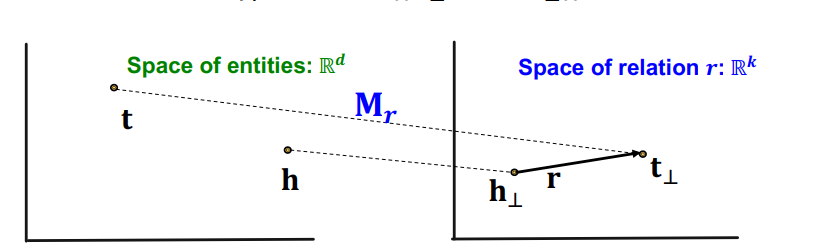
이는 위 그림과 같이 $h_\perp = M_r h, t_\perp = M_rt$ 로 h와 t를 모두 relation 공간으로 맵핑했을 때, 두 사영이 relation과 TranE의 관계를 가지도록 한다. 즉, 다음과 같은 score function을 가지게 된다.

f_r(h,t) = -||h_\perp + r - t_\perp||

4-1. 성질

symmetric

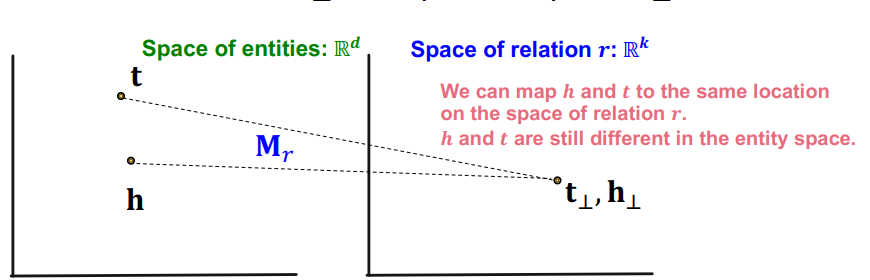
TranR은 대칭관계를 가질 수 있다 왜냐하면 TranE와 다르게 relation과 entity 공간을 분리했기 때문에 $h_\perp + r = t_\perp$ 면서 $t_\perp +r=h_\perp$ 도록 하는 조건인 $h_\perp = t_\perp$ 를 만들 수 있기 때문이다. 즉, h와 t가 실제로는 다른 노드이기 때문에, entity 공간에서 다른 위치에 있더라도 relation 공간에서 동일한 점으로 맵핑되도록 하면 대칭관계가 성립한다.

antisymmetric

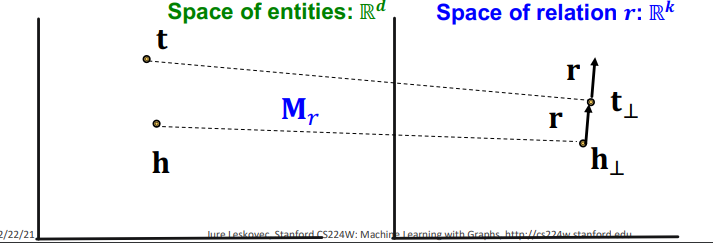
반대칭 관계역시 성립한다. 이는 relation 공간에서 TranE와 동일하게 생각하면 당연한데, $t_\perp = h_\perp + r$ 일때, $r \neq = 0$ 이면 $h_\perp \neq t_\perp + r$ 인 것은 당연하기 때문이다.

1-to-N

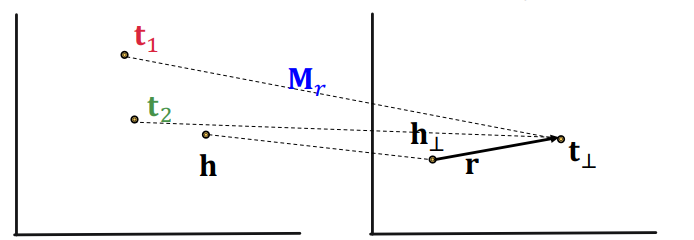
1-to-N 역시 성립한다. 대칭관계에서 다뤘듯이 entity 공간에서 다른 점이 relation에서 동일한 점으로 맵핑될 수 있기 때문에 tail에 해당하는 다양한 점이 relation 공간에서 동일한 점으로 맵핑될 수 있기 때문이다.

Inverse

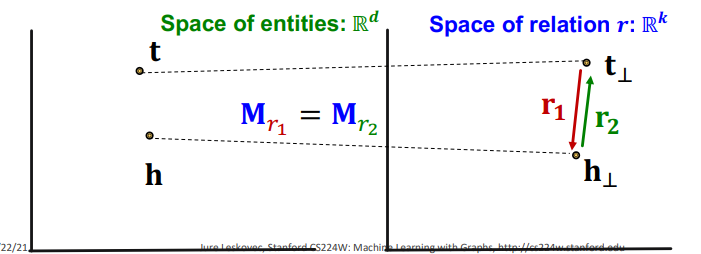
inverse 관계역시 성립한다. 이 역시 TranE와 동일하게 relation 공간을 생각하면 된다.

Composition
composition은 성립하지 않는다. 이는 TranR은 관계마다 다른 relation 공간을 생성하기 때문에,
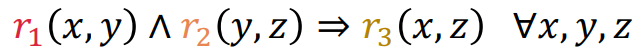위와 같은 관계를 성립하기 위한 $M_r$ 을 만들 수 있다는 보장이 없기 때문이다. 직관적으로는 위 관계를 성립하도록 하는 매니폴드인 $\{z | \exists y, f_{r_1} (x, y) =0, f_{r_2} = 0\}$ 은 매우 고차원의 매니폴드이기 때문에 단순하게 하나의 선형변환으로 표현될 수 없기 때문이라고 한다.

5. DistMult

TranE나 TransR 모두 두 벡터 간의 l1, l2 거리를 기반으로 목적함수를 구성하고 있다. 하지만 임베딩 벡터의 유사도를 측정하는 방법으론 l1, l2 거리 뿐만 아니라 코사인 유사도가 매우 자주 쓰인다. DistMult는 그래서 코사인 유사도를 기반으로 목적함수를 구성하게 된다.
entity와 relation을 모두 동일한 벡터 공간 $\mathbb{R}^k$ 에 올려놓고 목적함수를 다음과 같이 구성한다. $f_r(h, t) = <h, r, t> = \sum_i h_i \cdot r_i \cdot t_i$

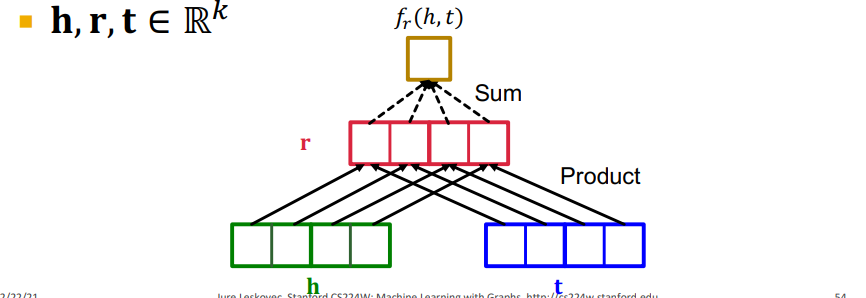
이걸 그림으로 표현하면 위와 같이 표현할 수 있는데, relation 벡터에 h와 t를 모두 element wise product한 다음 elment를 다 더한 값을 scoring function으로 사용하고 있다. 이때 우리는 h와 r이 주어진 상황에서 t를 찾는 것이기 때문에, $h \cdot r$ , h와 r의 element wise한 벡터에 t를 내적한 꼴이라고 볼 수도 있다. 즉, $h\cdot r$ 와 $t$ 의 내적값을 scoring function으로 사용하고 있다.

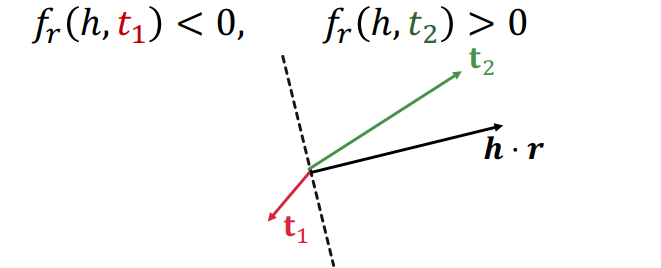
이렇게 보면 초평면의 개념으로 생각해볼 여지가 생기는데, 벡터 공간에서 $h\cdot r$ 의 벡터와 수직인 초평면을 기준으로 $h\cdot r$ 쪽에 $t$ 가 위치하면 scoring function은 양수가 되고, 반대편에 위치하면 음수가 될 것이다. 이때 $h\cdot r$ 이 초평면을 생성한다는 점을 기억하자.

5-1. 성질

1-to-N

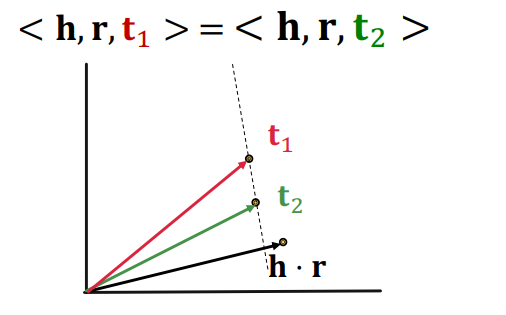
1-to-N은 만족한다. 왜냐하면 $h\cdot r$ 의 코사인 유사도를 계산하기 때문에, 위 그림처럼 초평면 위에 위치하는 $t$ 들이나, $h\cdot r$ 과 동일한 각을 가지는 직선 상에 위치하는 $t$ 들은 1-to-N을 만족하기 때문이다.

symmetric
기본적으로 DistMult는 element wise 곱을 이용하기 때문에 교환법칙이 성립하고, symmetric한 관계를 표현할 수 있다. 식으로 보자면 다음과 같다.
$f_r(h,t) = <h, r, t> = \sum_i h_i \cdot r_i \cdot t_i = \sum_i t_i \cdot r_i \cdot h_i = <t, r, h> = f_r(t, h)$

Antisymmetric
symmetric에서 이야기했듯이 교환법칙이 성립하기 때문에 반대칭 관계를 다룰 수 없다. 위의 식에서 $f_r(h, t) \neq f_r(t,h)$ 를 유도할 수 없기 때문이다.

Inverse

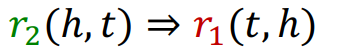
동일하게 element wise product이기 때문에 $f_{r_1}(h,t) = <h, r_1, t> = <h, r_2, t> = f_{r_2}(h, t)$ 가 성립하기 위해서는 $r_1 = r_2$ 여야 해서 inverse 관계를 다룰 수 없다. $r_1 = r_2$ 라는 것은 두 관계가 동일하다는 이야기인데, inverse는 다른 관계를 사용해서 head와 tail을 뒤집는 관계이기 때문이다.

Composition

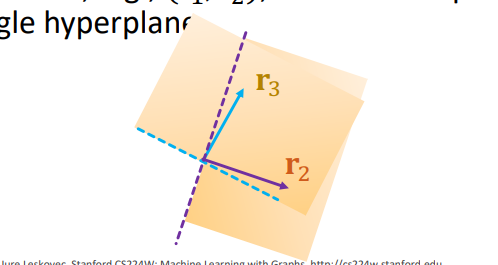
composition 역시 다룰 수 없다. 하나의 관계가 하나의 초평면을 만든다고 생각하면, 두 관계의 교집합은 두 관계의 초평면의 교집합을 의미하는데, 이는 하나의 초평면으로 표현이 불가능하기 때문이다.

6. ComlEx

지금까지는 모두 실수 체에서의 벡터 공간에서 임베딩 벡터를 다루었다. 하지만 이를 확장해서 복소수 체에서의 벡터 공간에서 임베딩 벡터를 다뤄보면 어떨까? 복소수 체는 켤레라는 개념을 가지기 때문에, 이것이 유용할 수 있을 것이다.

ComplEx는 DistMult를 복소수 체에서 다룬 방법론이다. 이때, 위와 같이 켤레 전치를 가지게 된다. 기본적인 구조는 ComplEx와 같지만 아래 그림처럼 scoring function에서는 실수 부분만 취하게 된다.

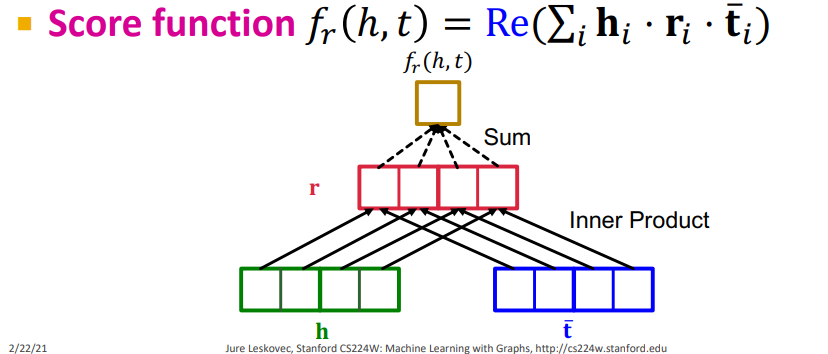
6-1. 성질

Antisymmetric
반대칭 관계를 표현할 수 있다. 이는 복소수 체로 옮겨오면서 얻게 되는 이득인데, 켤레전치를 이용하면 다음과 같이 반대칭 관계를 표현할 수 있게 된다.
$f_r(h, t) = \text{Re}(\sum_i h_i \cdot r_i \cdot \bar{t}_i)$
$f_r(t, h) = \text{Re}(\sum_i t_i, \cdot r_i \cdot \bar{h}_i)$

symmetric
대칭 관계역시 표현할 수 있다. 이때, relation의 허수 부분은 존재하지 않아야 한다.

\begin{aligned} \text{When } \text{Im}(r) = 0\\ f_r(h,t) &= \text{Re}(\sum_i h_i \cdot r_i \cdot \bar{t}_i)\\ &= \sum_i \text{Re}(r_i \cdot h_i \cdot \bar{t}_i)\\ &= \sum_i r_i \cdot \text{Re}(h_i \cdot \bar{t}) = \sum_i r_i \cdot \text{Re}(\bar{h}_i \cdot t_i) = \sum_i \text{Re}(r_i \cdot \bar{h}_i \cdot t_i)\\ &= f_r(t, h) \end{aligned}

Inverse
inverse 관계 역시 켤레 전치의 덕을 보게 된다.

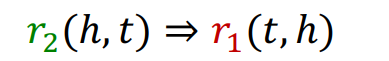
즉, 위의 관계에서 $r_2 = \bar{r}_1$ 이라면 자연스레 inverse 관계를 표현할 수 있다.

Composition
composition은 DistMult와 동일한 이유로 표현할 수 없다. ComlEx도 어쩔 수 없이 DistMult의 구조를 가져왔기 때문에 초평면의 개념을 사용하기 때문이다.

1-to-N
1-to-N 역시 DistMult에서 표현가능하기 때문에, 표현가능하다.

7. 정리

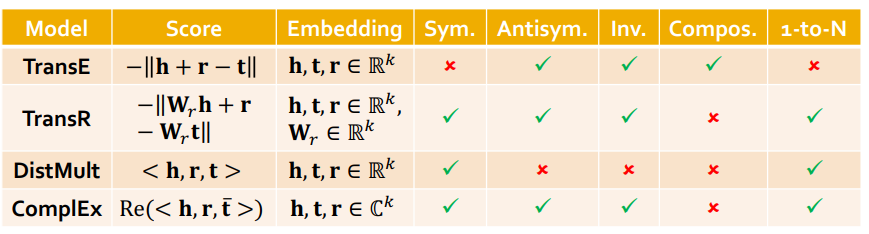
지금까지 다룬 지식 그래프 모델을 정리하면 위와 같다. 보면 알 수 있지만, 모든 관계를 표현할 수 있는, 모델은 없다. 결국 표현할 필요가 있는 관계에 따라 모델을 선택해야 한다. 수업에서는 TransE가 가장 빠르기 때문에, 기본적으로 시도해보고 다른 것들을 시도해보는 것을 추천하고 있다.