SH-ESD 이상치 탐지

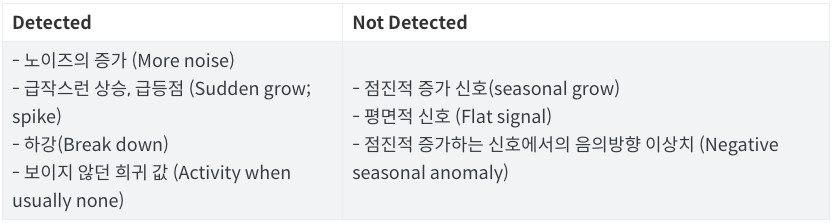
SH-ESD란?

• Seasonal Hybrid ESD를 의미
• 결국 축적된 시간동안 정적인 점분포에 초점을 맞추는 Point anomaly 와, 시계열적인 동적인 특성에 주안을 두는 Context anomaly로 구분 지을수 있다.
• SH-ESD는 Context anomaly에 해당함

SH-ESD 등장 배경

기존 이상탐지 방법의 한계

• 잘못된 계산 지표 (Using Wrong Metric)
  • 기존의 단순 평균$\mu$, 표준편차$\sigma$를 이용하는 방식 자체가 outlier를 포괄하여 계산하므로 이상값에 취약
• Multi-modality에 취약: 평규과 표준편차가 seasonality, trend 등에 의해 변화되어 outlier를 놓치게 되는 경우가 발생

S-H-ESD 기법의 이상탐지 방법

• Use Robust Statistics/Metric:
  • Median Absolute Deviation(MAD)
  • Grubb’s Test& Generalized Extreme Studentized Deviate (ESD)
• Remove impact of seasonality and trend (Multi-modality aware):
  • Seasonal Trend decomposition using Loess(STL)

S-H-ESD 기법을 이해하기위해 알아야하는 개념

• Median Absolute Deviation(MAD)
• Student t-distribution
• Extreme Studentized Deviate (ESD) test
• Generalized ESD
• Seasonal Trend decomposition using Loess(STL)

1) Median Absolute Deviation(MAD) - 중위수(중앙값) 절대 편차

• $MAD = median(|{X_i} - median(X)|)$
• 관측값에서 중앙값을 뺀 값들의 중앙값. 양적 자료의 퍼짐을 알고 싶을 때, 표본분산과 표준편차 보다 이상치에 덜 영향을 받는 강건성(robustness) 있는 분산 측정 방법.

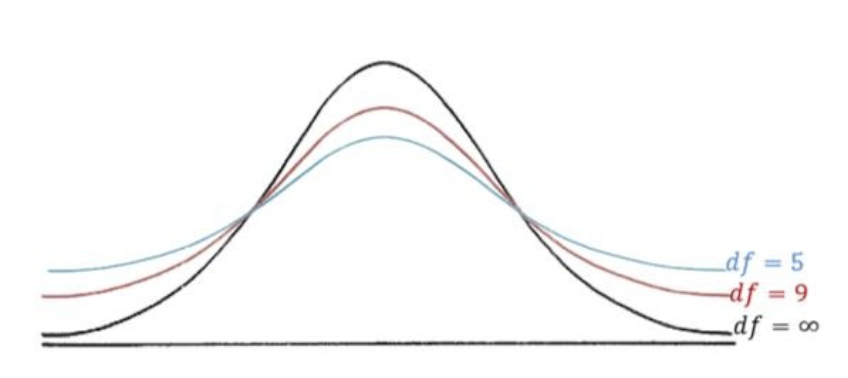
2) Student t-distribution

• 자유도에 따라 형태가 다른 분포

• Z분포처럼 표준정규분포는 아니지만, 평균이 0이고 좌우대칭의 분포인 정규분포

• 표준편차가 1보다 크다.

• 표본의 크기나 자유도가 무한대라면, t분포는 표준정규분포가 된다 $\Rightarrow$ 즉, 자유도가 커질수록 표준정규분포가 된다.

  • 따라서, t-분포는 정규분포에서 개의 표본들을 확률변수로 정의한 확률 분포이다. 이 확률 분포 또한 정규분포

• 표본평균 : ${\overline{X}}={\frac {1}{n}}{(X_{1}+\cdots +X_{n})}$

• 표본분산 : ${S^{\;2}={\frac {1}{n-1}}\sum _{i=1}^{n}\left(X_{i}-{{X}}\right)^{2}}$

• ${V=(n-1){\cfrac {S^{2}}{\sigma ^{2}}}}$

• ${Z=\left({\overline {X}}-\mu \right){\cfrac {\sqrt {n}}{\sigma }}}$

• ${T\equiv {\cfrac {Z}{\sqrt {V/\nu }}}=\left({\overline {X}}-\mu \right){\cfrac {\sqrt {n}}{S}}}$

• ${Z, T}$ 를 비교해보면 분모에 ${{\sigma}, {S}}$가 있는게 차이

  • 모표준편차를 썻냐, 표본의 표준편차를 썻냐 차이
  • 따라서 모분산을 모를때 $\Rightarrow$ 표본을 가지고 모집단을 추정을 해야할때 $t$-분포 를 사용한다.

• 즉, ${\displaystyle T}$ 에는 ${\displaystyle \sigma ^{2}}$가 사용되지 않으므로, 이 분포는 분산을 모를 때의 평균값 ${\displaystyle \mu}$ 를 추정하는 데에 사용이 가능하다. 이때 ${\displaystyle T}$의 분포는 자유도 n-1인 t-분포가 된다.

3) Grubb’s test(=ESD test)

• 단일 이상치를 테스트 하는데 ESD test 방법은 널리 알려진 기법이다. ESD 검증 방법의 상세한 설명은 본 보고서에서 생략하며, 주요 수식표현은 아래와 같다.

• ESD 검정은 아래와 같은 귀무가설/대립가설을 통해 검정한다.

  • 귀무가설 : "데이터셋에 이상치가 없다"(There are no outliers in the data set)
  • 대립가설 : "데이터셋에 이상치가 하나는 존재한다"(There is exactly one oulier in the data set)

• 아래 정의와 같은 G 값을 통해 outlier 인지 판별한다.

  • $\overline Y$ : 표본평균(sample mean)

  • $s$ : 표준편차(standard deviation)

  • $G$ = Y값중 표본 평균이랑 뺏을때, 그값의 절대값이 가장 큰값 ÷ 표준편차

  • $G$=${\cfrac {\displaystyle \max _{{i=1,\ldots ,N}}\left\vert Y_{i}-{\bar {Y}}\right\vert }{s}}$

  • $G$ $>$ ${\cfrac {N-1}{{\sqrt {N}}}}{\sqrt {{\cfrac {t_{{\alpha /(2N),N-2}}^{2}}{N-2+t_{{\alpha /(2N),N-2}}^{2}}}}}$ 를 만족하면, $H_0$ 기각

  • (참고) crtical value = ${\cfrac {N-1}{{\sqrt {N}}}}{\sqrt {{\cfrac {t_{{\alpha /(2N),N-2}}^{2}}{N-2+t_{{\alpha /(2N),N-2}}^{2}}}}}$

최대값과 최소값을 둘 다 검정하는 two-sided test 에서, 이상치가 없다는 귀무가설 $H_0$은 G값이 significance level( $\alpha$ ) 바깥에 있다면 귀무가설 $H_0$는 기각된다.

ESD 테스트는 정상성 (normality) 를 가정하고, 단일 이상치를 탐지하는데 적합하다는 한계 때문에, 시계열과 같은 연속적 데이터에서 지속적으로 이상탐지를 해야하는 경우, 아래와 같은 Generalized ESD 의 사용이 권장된다.

Generalized Extreme Studentized Deviate(Generalized ESD)

• Generalized ESD 는 Grubb’s test와 달리 여러개의 outlier를 가정한 검정방법임. 가장 높은 G 밸류를 제거해 나가면서 지속적으로 순회하여 평균과 표준편차를 업데이트해나가는 방식.
• 위에 명시된 Critical Value(임계값) 또한 지속적으로 업데이트 되며, 를 만족하는 $i$ 가 이상값의 개수를 결정하게됨. 본 검정방법은 앞선 Grubb’s test 보다 여러개의 outlier를 검출 할 수 있다는 장점이 있으나,
• 여전히 정규성을 가정하고 있으므로, 정규성 테스트 선행이 되어야 하고, 계절성(seasonality)을 고려하지 않는 단점이 있다. $\Rightarrow$ 이러한 단점 때문에 STL도 하게됨

4) Seasonal Trend decomposition using Loess(STL)

STL은 시계열 데이터에서 계절성, 추세, 잔차 세가지 패턴요소로 분해하는 기법으로 seasonality와 trend를 제거하면, 이상탐지에 적합한 residual만 남게 된다.

References

• 이상탐지 Anomaly Detection
• IBM - Modified z score
• Modified z score 2