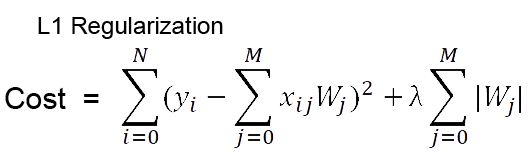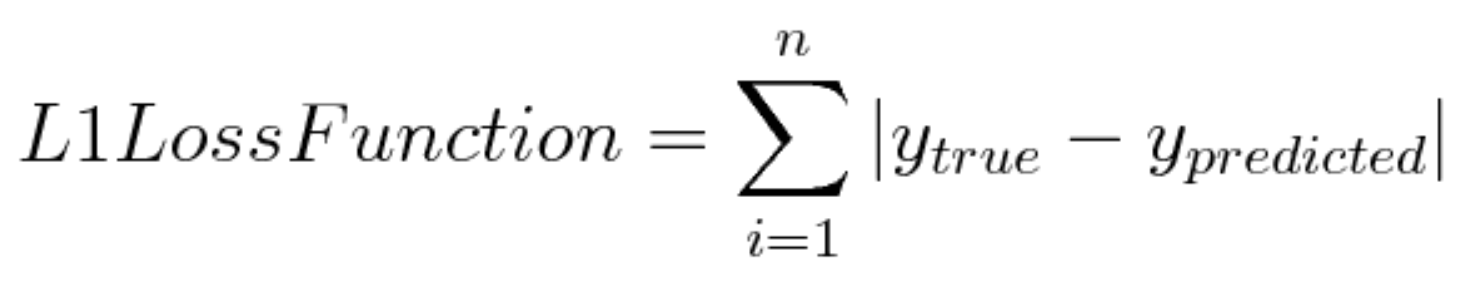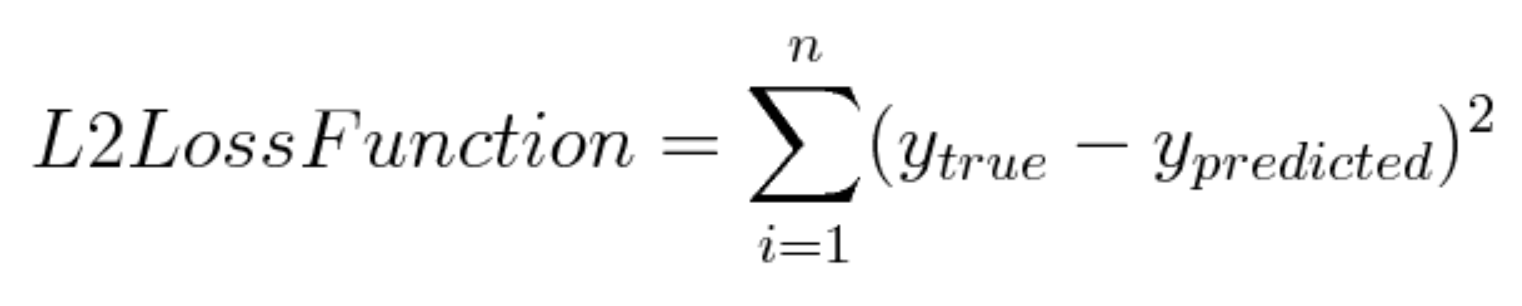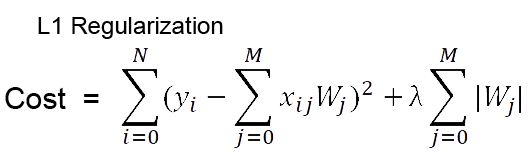
정규화(Regularization) 요약

정규화(Regularization)의 목적

• 모델을 조금 더 General하게 만들고자 하는 것 = 모델의 오버피팅(Overfitting)을 줄이고자 하는 것
• 모델을 학습시킨다는건 결국 모델의 Weight matrix를 좋은 방향으로 업데이트해나가는 것
  • Weight 중 일부가 학습과정 중 과도하게 커져버린다면, 몇몇개의 인풋에 극단적으로 의존하는 상황이 벌어지고, 이 경우 모델의 일반화 성능은 감소할 것
  • 특정 Weight가 과도하게 커지지 않게끔 락(Lock)을 걸어주는 역활을 L1, L2 정규화가 해줍니다.
  • (참고) 모델의 Weight matrix size가 너무 작다면, 이런일이 발생할 수 있습니다. 때문에 뉴럴넷를 설계할 때에는, 충분히 Weight matrix size를 Sparse할 수 있게끔 구축해야합니다
• 따라서, 정규화는 weight 정규화 를 뜻한다. = weight를 정규화해서 너무 커지는 것을 방지해준다.

L1 Regularization

• 수식
  
  
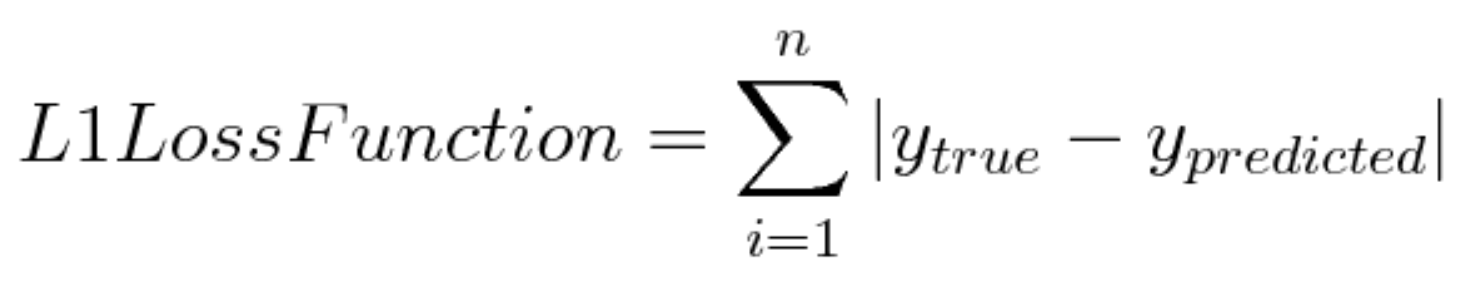
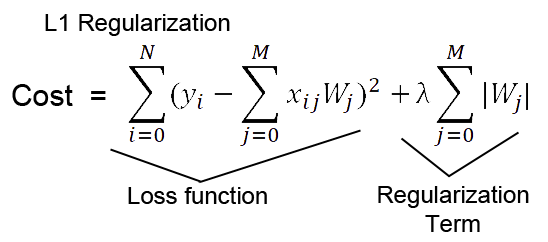
• 위 스샷들 중에서 Cost의 Loss function 부분의 summation of xw 부분이 첫번째 스샷에서 $y_{predicted}$를 의미
• L1 Regularization이라는 건 결국 L1 Loss 에 Regularization Term을 붙인 것
• 기존 Loss에 절댓값만큼의 어떤 족쇄(패널티)를 달아줌으로써 Cost가 더 커지게 만든 셈인데, 이를 통해 특정 Weight의 중요도가 커지는 걸 막는다는 느낌(Cost가 커지면 Weight 중요도가 줄어드니깐)
• 저기서 $\lambda$가 작아질 수록, 약한 정규화가 적용
• Sparse feature에 의존한 모델에 L1 Regularization을 사용하면, 불필요한 Feature에 대응하는 Weight를 정확히 0으로 만들어버려, Feature selection의 효과를 냄
• (참고) L1 Regularization을 사용하는 선형 회귀 모델을 Lasso model이라고도 합니다.

L2 Regularization(Ridge Model)

• 수식
  
  
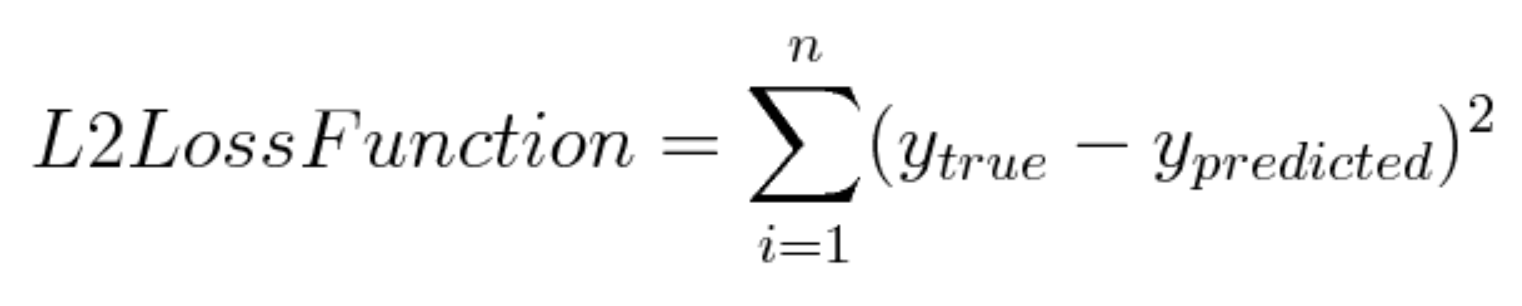
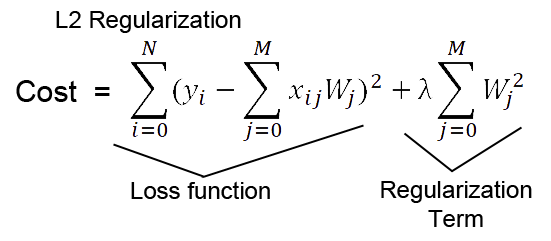
• L1 Reg와 같이, L2 Reg도 기존의 L2 Loss에 Regularization Term을 붙이는 방식.
• 다만 불필요한 Feature(이상치)에 대응하는 Weight를 0에 가깝게 만들 뿐, 0으로 만들지는 않습니다.
• 0이 될 수 있는(=강하게 밀어붙이는) L1 Reg반해 L2 Reg은 선형 모델의 일반화 능력을 항상 개선시키는 것으로 알려져 있음.
• (참고) 마지막으로 L2 Regularization을 사용하는 선형 회귀 모델을 Ridge model이라고 합니다.

엘라스틱넷

• 엘라스틱넷(Elastic Net)은 제약식에 $L1$, $L2$ norm 모두 쓰는 기법

라소 vs 릿지 vs 엘라스틱넷

• 표
  
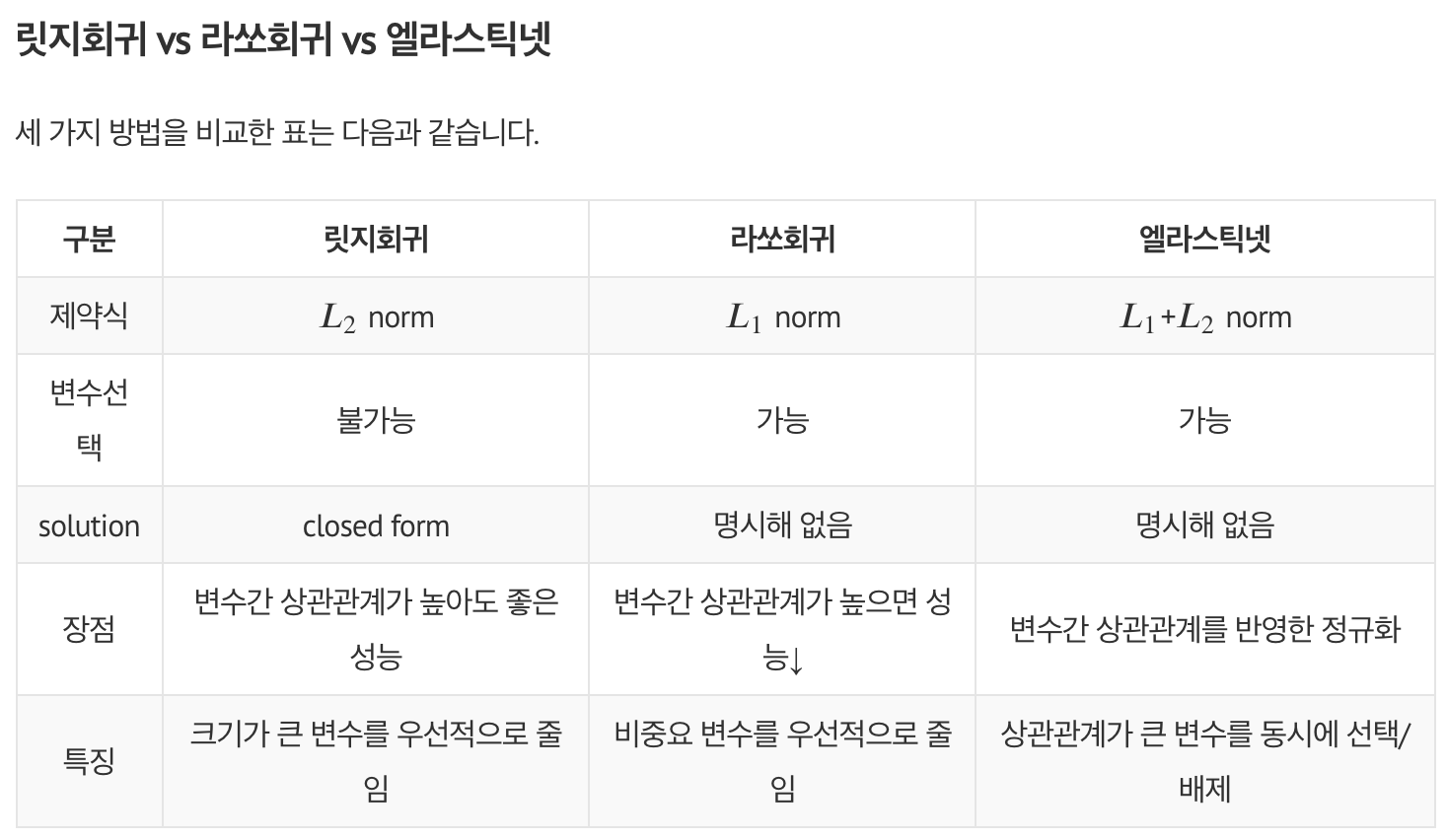
• 그림
  

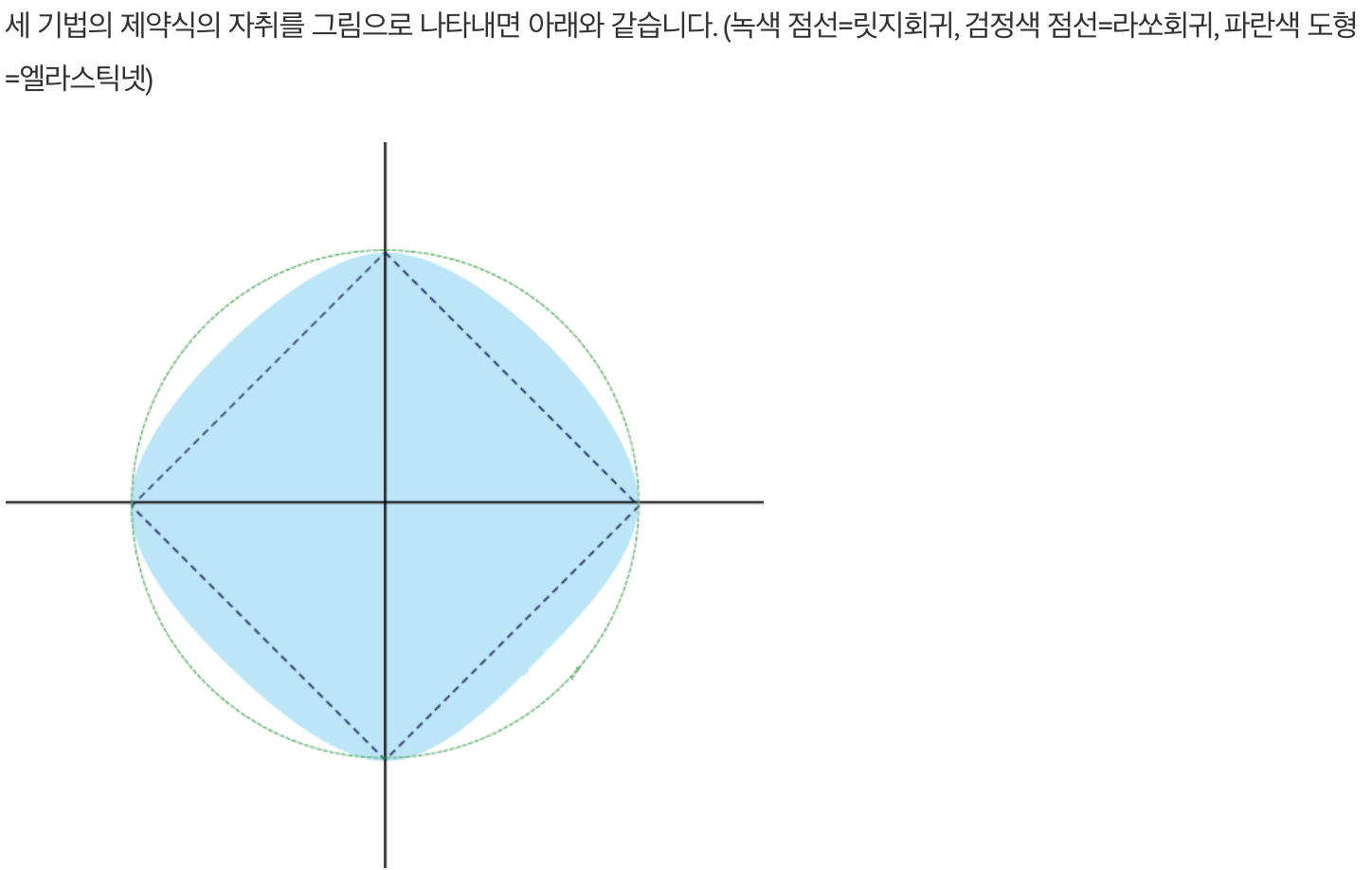
References

• L1, L2 Norm, Loss, Regularization?
• Cost 수식 스샷 참고
• ratsgo - 라소 vs 릿지 vs 엘라스틱넷 비교 관련 자료
• (참고 1) 딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명
• (참고 2) L1, L2 regularization, Ridge와 Lasso의 차이점 (201023)