1.개괄
데이콘이나 캐글과 같은 데이터 분석 경진 대회에서는 분류 문제를 평가할 때 주로 F1-score나 ROC-AUC를 평가 지표(metric)로 사용합니다. 이 두 지표는 모두 분류 모델의 성능을 나타내지만, 측정하는 관점이 다릅니다. 후술하겠지만, F1-score는 정밀도(Precision)와 재현율(Recall)의 조화 평균으로, 특정 임계값(threshold)에서 모델이 얼마나 균형 있게 양성 클래스를 정확히 예측했는지를 나타냅니다. 반면 ROC-AUC는 임계값을 변화시키면서 모델의 전체적인 분류 능력을 평가하는 지표로, 양성과 음성을 얼마나 잘 구분하는지를 종합적으로 측정합니다.
2. 예시
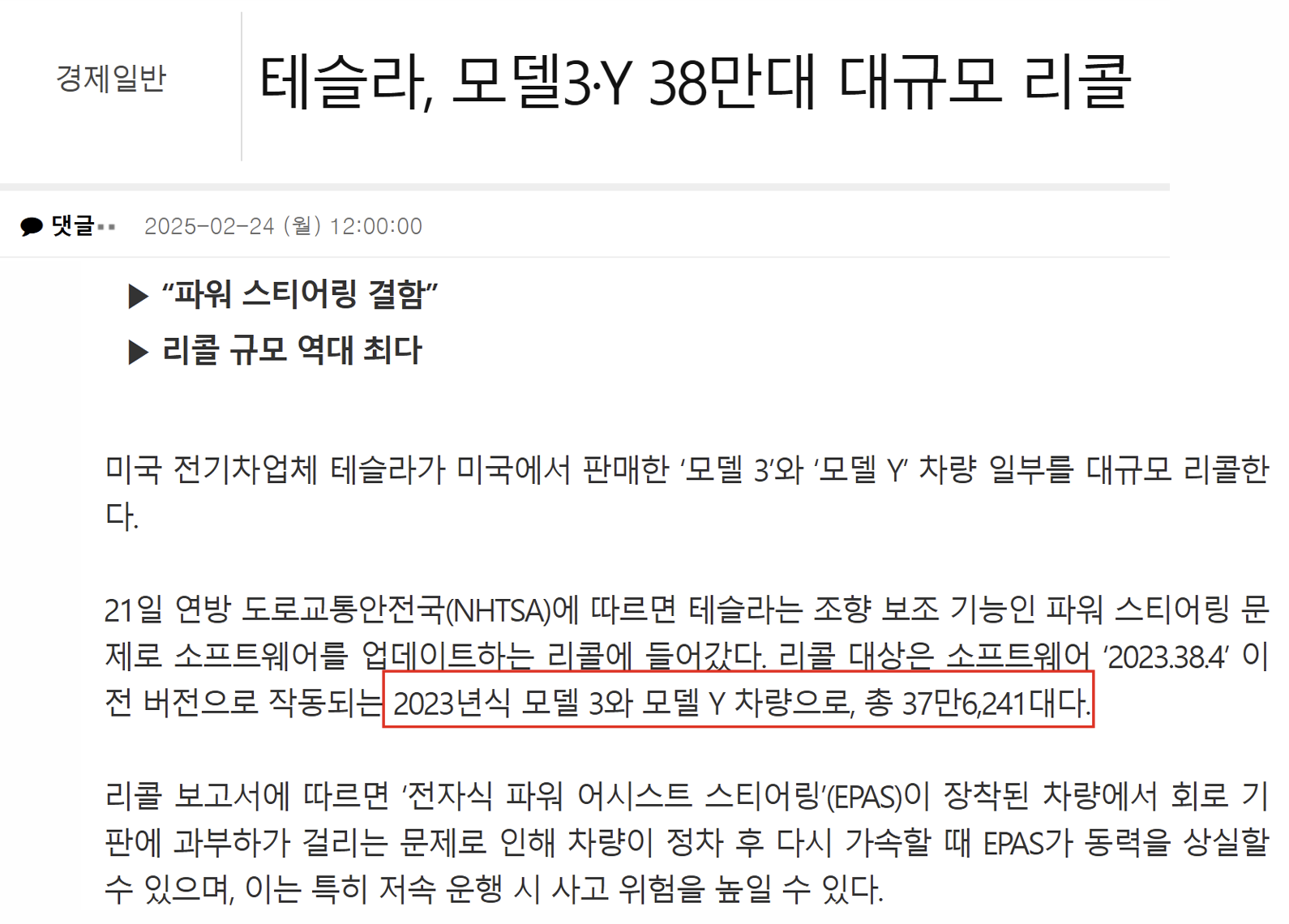
위의 글은 테슬라가 차량을 리콜했다는 기사입니다. 테슬라가 차량을 리콜하는 상황을 가정해보면, 모델 3와 모델 Y를 모두 회수한 뒤 각 차량에 문제가 있는지를 검증하게 됩니다. 이 과정에서 불량 검증 모델은 차량이 불량인지 여부를 판정하며, 만약 불량으로 예측되면 부품 교체 등의 조치를 취하고, 불량이 아니라고 판단되면 차량을 그대로 고객에게 제공하게 됩니다. 이러한 맥락을 바탕으로, 분류 모델과 평가 지표에 대해 이어서 설명하고자 합니다.
3. F1-Score에 이르는 길: 임계값
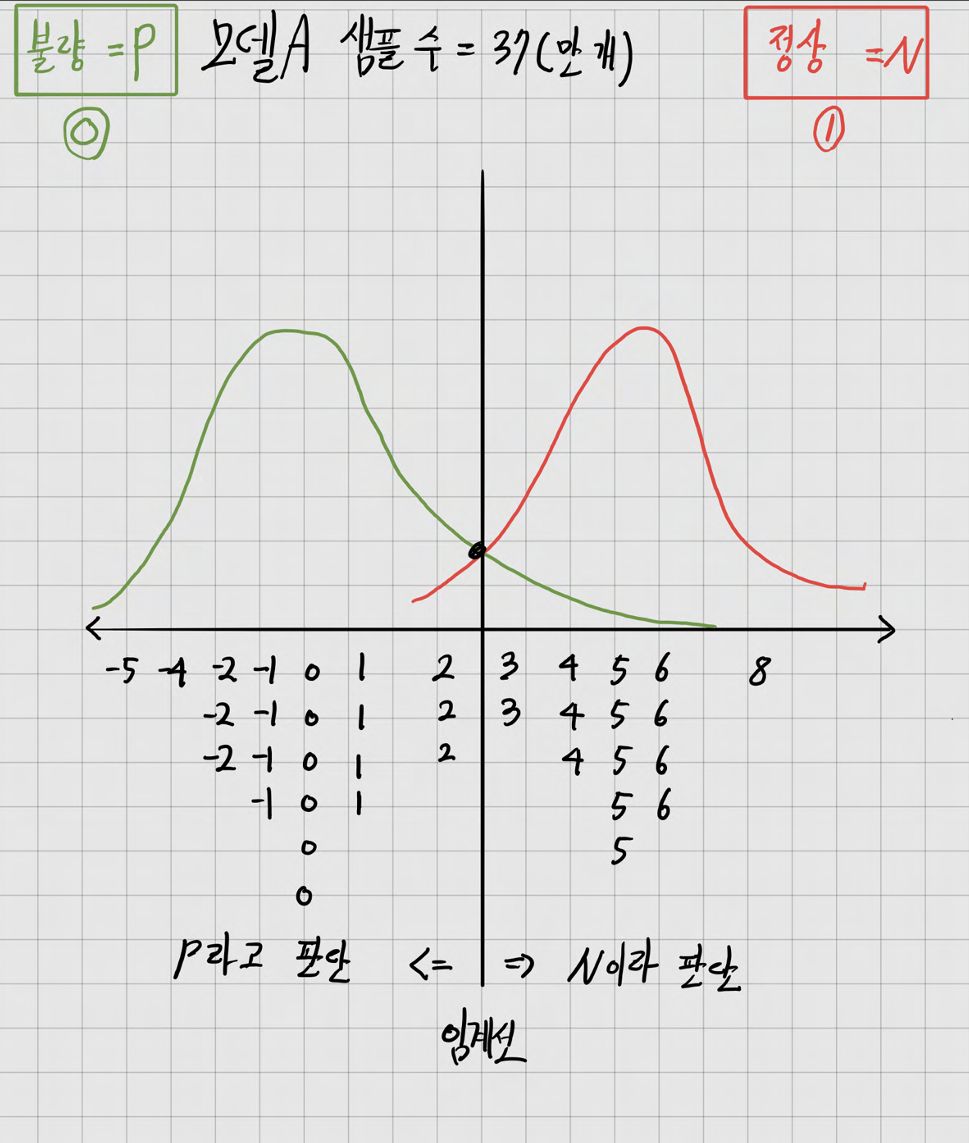
불량 검증 모델은 임계값(threshold)을 기준으로 왼쪽 영역을 Positive(불량), 오른쪽 영역을 Negative(정상) 으로 분류합니다. 이때 임계값을 두 분포(정상과 불량)의 교점에 위치시키는 것이, 초록색과 빨간색 분포가 가장 겹치는 지점에서 경계를 나누는 것이기 때문에, 전체적인 정답률(Accuracy) 을 최대화하는 데 일반적으로 유리해 보입니다. 그러나 임계값을 단순히 교점에 두는 것이 항상 최선은 아닙니다.

비가 오는 날이 비 오지 않는 날에 비해 압도적으로 적은 상황에서는, "비가 오지 않는다"고만 예측해도 전체 정확도가 90%에 달할 수 있습니다. 하지만 이처럼 다수 클래스를 무조건 예측해 높은 정확도를 얻는 모델을 좋은 모델이라고 할 수는 없습니다. 실제로 중요한 것은 소수 클래스(비 오는 날)도 정확히 잡아내는 능력이기 때문입니다. 이런 문제의식에서 정확도(Accuracy) 대신 정밀도(Precision)와 재현율(Recall) 을 함께 고려하는 F1-Score라는 새로운 평가 지표가 필요하게 되었습니다.
3.1 Precision과 Recall의 긴장관계
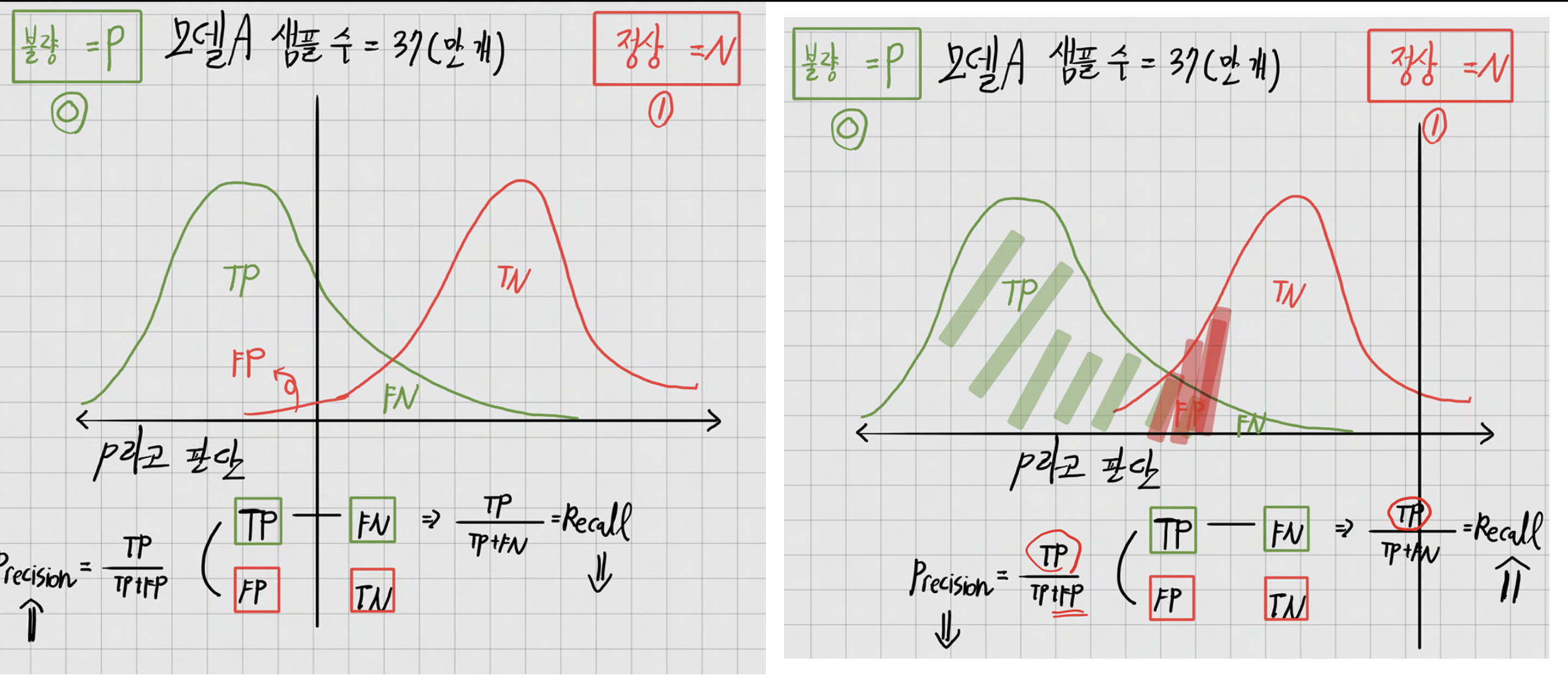
임계값(threshold)을 오른쪽으로 밀수록, 불량 판정을 받는 차량이 늘어나면서 불량을 최대한 많이 잡아내게 됩니다. 그러나 이 경우 정상 차량도 불량으로 오판하는 경우가 많아져, Precision(정밀도) 가 떨어지게 됩니다. 반대로 임계값을 왼쪽으로 밀면, 정상 차량을 정상으로 판별하는 비율은 올라가지만, 불량 차량을 놓치는 경우가 많아져 Recall(재현율) 이 감소하게 됩니다. 즉, Precision과 Recall은 서로 긴장 관계(trade-off 관계) 에 있으며, 임계값 설정에 따라 한쪽을 높이면 다른 쪽이 희생되는 구조를 가집니다.
Accuracy는 단순히 전체 정답 비율만을 고려하는 지표로, Precision과 Recall 사이의 균형을 반영하지 못합니다. 기술적으로 표현하면, Accuracy는 Precision과 Recall을 고려하지 않은 채, 다수 클래스에 편향된 결과에도 높은 점수를 줄 수 있습니다. 따라서 Precision과 Recall이 함께 낮아지는 것을 억제하고, 둘의 균형을 평가할 수 있는 별도의 지표가 필요해졌습니다. 이 요구를 충족하기 위해 등장한 것이 바로 F1-score입니다.
3.2 F1-score
임계값을 조정하면서 발생하는 Precision과 Recall의 변화를 살펴보면,
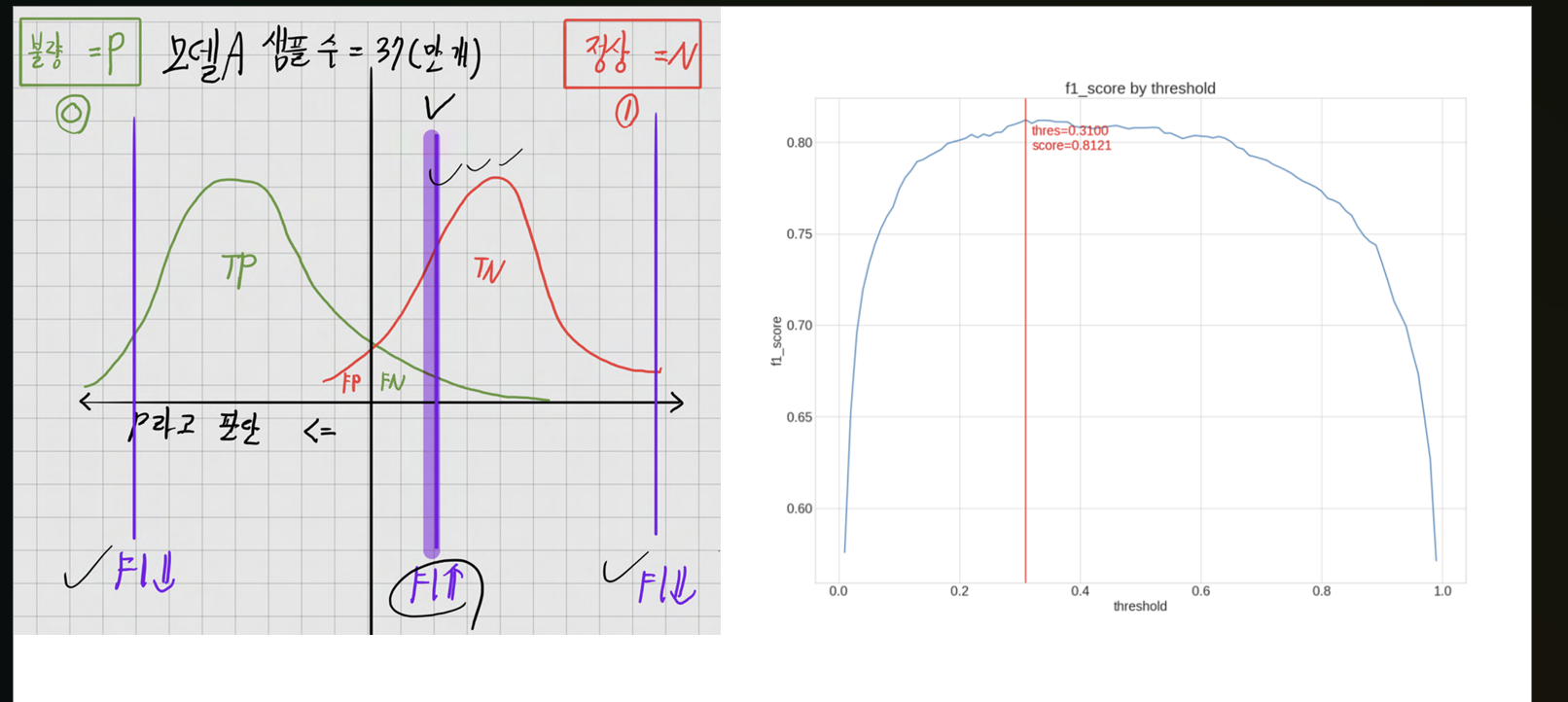
임계값을 오른쪽으로 밀면 Recall은 증가하지만 Precision은 감소하고, 임계값을 왼쪽으로 밀면 Precision은 증가하지만 Recall은 감소하는 패턴을 보입니다. F1-score는 이 두 가지 상황을 모두 고려하여, Precision과 Recall이 모두 높은 임계값 설정을 찾아내는 데 활용됩니다.
수식으로 F1-score는 다음과 같이 정의됩니다:
F1 = 2 / (1/Precision + 1/Recall)이는 Precision과 Recall의 역수 평균의 역수입니다. 이 식의 특성상 Precision 또는 Recall 중 하나라도 작아지면 분모가 커지며 F1-score는 급격히 감소합니다. 반대로 Precision과 Recall이 모두 1에 가까울 때 F1-score는 1이 됩니다. 따라서 F1-score의 범위는 (0, 1]이며, 둘 다 고르게 높은 상황에서 F1-score 또한 높아집니다. 요약하면, Precision과 Recall을 균형 있게 모두 높이는 것이 높은 F1-score를 달성하는 핵심입니다.
3.3 만약에 테슬라 직원이라면.....
테슬라 소속 직원이 리콜된 37만 대 차량의 불량 여부를 검출하는 업무를 맡았다고 가정해봅시다. 이 경우, 정상 차량을 불량으로 판단하는 것은 불필요한 차량 교체 비용이 발생하는 정도의 문제를 일으킬 수 있지만, 인명 피해로 이어지지는 않습니다. 반면, 불량 차량을 정상으로 오판하면 추후 교통사고로 인한 심각한 인명 피해가 발생할 수 있습니다. 따라서 이 작업에서는 Recall(재현율) 을 더 민감하게 고려해야 합니다. 즉, F1-score를 최대화하는 임계값을 설정하되, 그 부근에서도 특히 Recall을 중시하는 방향으로 모델을 운영하는 것이 바람직합니다.
4. AUC-ROC
그러나 F1-score만으로 모델을 평가할 때에는 몇 가지 한계가 있습니다. F1-score는 단일 임계값에 종속적이기 때문에, 같은 모델이라도 임계값을 다르게 설정하면 다양한 F1 값을 얻게 됩니다. 이런 이유로 하나의 고정된 지표로 모델 전체의 성능을 대표하기 어렵다는 문제가 생깁니다. 이 한계를 보완하기 위해, 임계값에 상관없이 모델의 분류 성능을 평가할 수 있는 지표가 필요하게 되었고, 그 지표가 바로 AUC-ROC입니다.
4.1 정의

AUC-ROC를 이해하는 방법은 다음과 같습니다.
임계값을 변화시키면서, 초록색(정상) 분포의 누적 비율과 빨간색(불량) 분포의 누적 비율을 각각 X축(FPR, 거짓 양성 비율)과 Y축(TPR, 진짜 양성 비율)으로 설정하여, 임계값을 오른쪽에서 왼쪽으로 점차 이동시켜 나갑니다. 이 과정을 통해 얻은 여러 좌표를 연결하면 하나의 곡선이 만들어지는데, 이것이 바로 ROC 곡선입니다.
만약 모델의 분류 성능이 높아 정상과 불량 분포를 멀리 떨어뜨려 놓을 수 있다면, 임계값을 조정할 때 Y축(TPR)이 먼저 빠르게 상승하고 X축(FPR)은 느리게 증가하게 됩니다. 즉, 곡선이 급격하게 위로 솟구치는 특성을 가지게 되고, 결과적으로 곡선 아래의 면적(AUC, Area Under Curve) 이 커지게 됩니다. 따라서 AUC 값은 임계값과 무관하게 모델의 전체적인 분류 성능을 종합적으로 나타내는 지표라고 할 수 있습니다. AUC가 클수록 모델이 정상과 불량을 잘 구분하고 있다는 것을 의미합니다.
4.2 F1-score와 AUC-ROC의 관계
F1-score와 AUC-ROC는 모두 분류 모델의 성능을 평가하지만, 측정하는 방식과 초점이 다릅니다. F1-score는 하나의 특정 임계값을 기준으로 Precision과 Recall의 균형을 평가하는 지표입니다. 따라서 임계값을 어떻게 설정하느냐에 따라 F1-score 값이 크게 달라질 수 있습니다. 예를 들어, 같은 모델이라도 임계값을 다르게 설정하면 F1-score가 높게 혹은 낮게 변할 수 있습니다.
반면, AUC-ROC는 모든 가능한 임계값을 통합적으로 고려하여 모델의 분류 능력을 평가합니다. ROC 곡선은 임계값을 0부터 1까지 변화시키며 얻은 TPR과 FPR 값을 기반으로 만들어지며, AUC는 그 곡선 아래 면적을 수치화한 값입니다. 따라서 AUC는 특정 임계값에 의존하지 않고, 모델이 양성과 음성을 얼마나 잘 구분하는지를 총체적으로 평가합니다.
정리하면, F1-score는 "특정 임계값에서 모델이 얼마나 정밀하고 재현성이 좋은가"를 나타내고, AUC-ROC는 "임계값을 어떻게 설정하든 모델이 전반적으로 양성과 음성을 얼마나 잘 구분하는가"를 보여줍니다.
5. 결론
분류 모델의 성능을 평가할 때, F1-score와 AUC-ROC는 각각 다른 관점을 제공합니다. F1-score는 특정 임계값에서 Precision과 Recall의 균형을 평가하고, AUC-ROC는 임계값에 상관없이 모델의 전반적인 분류 능력을 평가합니다.
현실 문제에서는 단순히 Accuracy만으로 모델을 평가할 수 없는 상황이 많습니다. 특히 불량 검출처럼 한쪽 클래스가 훨씬 중요한 경우, F1-score를 통해 Precision과 Recall의 균형을 고려하는 것이 필요합니다. 그리고 임계값 설정에 의존하지 않는 종합적인 모델 평가를 위해 AUC-ROC를 함께 살펴야 합니다.
요약하면, F1-score는 "지금 설정된 임계값에서 모델이 얼마나 좋은가, AUC-ROC는 "모델이 임계값에 흔들리지 않고 얼마나 강건한가" 를 보여줍니다. 따라서 두 지표를 함께 활용하여, 모델의 성능을 더 입체적이고 정교하게 평가하는 것이 바람직합니다.
