💡선형모델
- 입력 특성에 대한 선형 함수를 만들어 예측 수행
- 회귀의 선형 모델 예측
직선 방정식을 이해하기 쉽도록 그래프의 중앙을 가로질러 x, y축을 그림 - 특성이 많은 데이터셋이라면 선형모델은 매우 훌륭한 성능 낼 수 있음
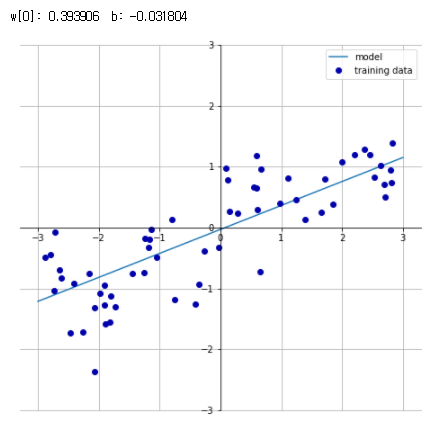
🔔 선형회귀(최소제곱법)
- 예측과 훈련 세트에 있는 타깃 y 사이의 평균제곱오차를 최소화하는 파라미터 w와 b를 찾는 것
- 평균제곱오차 : 예측값과 타깃값의 차이를 제곱하여 더한 후 샘플 개수로 나눈것
- 매개변수가 없는 것이 장점 -> 모델의 복잡도 제어방법도 없음
- from skelearn.linear_model import LinearRegression
🔔 선형 모델
릿지회귀(Ridge)
- 최소적합법에서 사용한 것과 같은 예측함수 사용
- 가중지 절댓값을 가능한 작게 : 가중치(w)의 모든 원소가 0에 가깝게 되기를 원함 -> 모든 특성이 출력이 주는 영향을 최소한으로(기울기 작게)
- 규제
중요한 feature 특성을 골라서(가중치) 학습
feature에게만 가중치를 주고 나머지는 가중치를 약하게
과대적합이 되지 않도록 모델을 강제로 제한
릿지 회귀에 사용하는 규제방식 : L2 규제
라쏘회귀(Lasso)
- 릿지와 같이 계수를 0에 가깝게 하려고 함
- 라쏘 회귀에 사용하는 규제방식 : L1 규제 -> 어떤 계수는 정말 0이 됨 -> 모델에서 완전히 제외되는 특성이 생긴다는 뜻(특성 선택이 자동으로 이뤄진다고 볼 수 있음)
- 일부 계수를 0으로 만들면 모델 이해가 쉬워지고 모델의 가장 중요한 특성을 드러내줌
규제 - L1, L2
L2 : 모든 feature사용 가중치는 강하게, 약하게 조절 -> 릿지
L1 : 모든 feature 사용하지않고 관련있는 feature만 골라서 가중치 부여 즉, 나머지 feature는 다 0으로 줌 -> 라쏘
🚗 자동차 연비 예측
- 단순회귀 : feature1
- 다항회귀 : feature 여러개
🐼 문제정의
문제정의 : 회귀 모델을 사용하여 1970년대 후반/1980년대 초반 자동차 연비(MPG)예측
# 라이브러리 임포트
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib as mpl
import matplotlib.pyplot as plt
# 한글 깨짐 방지
%config InlineBackend.figure_format = 'retina'
!apt -qq -y install fonts-nanum
import matplotlib.font_manager as fm
fontpath = '/usr/share/fonts/truetype/nanum/NanumBarunGothic.ttf'
font = fm.FontProperties(fname=fontpath, size=9)
plt.rc('font', family='NanumBarunGothic')
mpl.font_manager._rebuild()📋 데이터 준비
df = pd.read_csv('/content/auto-mpg.csv', header=None)
df.columns = ['mpg','cylinders','displacement','horsepower','weight',
'acceleration','model year','origin','name']
df.head()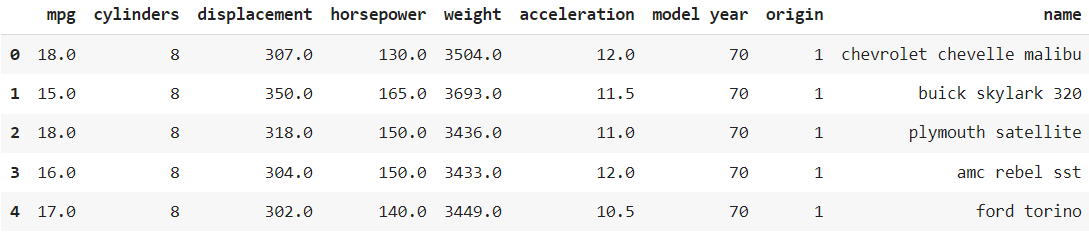
📋 데이터 전처리
df.info()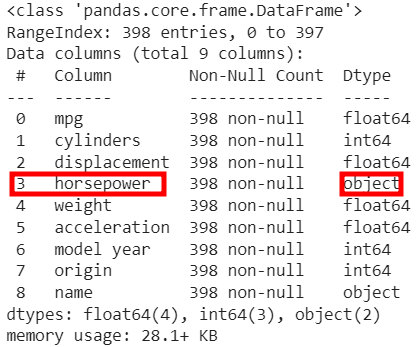
👀 horsepower가 왜 숫자형이아니고 object일까 ????? 의심해보기
👀 df['horsepower'].unique()로 확인해보면,

숫자형태가 아닌 물음표가 들어있음을 볼 수 있음
물음표 제거 방법 ?
- '?'를 NaN형태로 바꾸기
- dropna()로 NaN제거
- 'horsepower'의 dtype을 float으로 변환
# 1) '?'를 NaN형태로 변경 df['horsepower'].replace('?', np.nan, inplace=True) # 2) np.nan 값을 삭제 df.dropna(subset=['horsepower'], axis=0, inplace=True) # 3) 데이터타입 object -> float64로 변경 df['horsepower'] = df['horsepower'].astype('float')
👀 horsepower이 float64로 변경되고 개수가 398개에서 물음표 여섯개가 제거된 392개가 되었음
📈 단순회귀
독립변수1개, 데이터셋 분리
# 단순 회귀 -> 독립변수(feature) 1개 weight
X = df[['weight']]
y = df['mpg']
# 데이터셋 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=7) # 70:30모델 설정 후 학습
from sklearn.linear_model import LinearRegression, Ridge, Lasso
# 선형 제곱법
lr = LinearRegression().fit(X_train, y_train)
print('훈련세트의 R2 : ', lr.score(X_train, y_train))
print('테스트세트의 R2 : ', lr.score(X_test, y_test))
# 훈련세트의 R2 : 0.6874675811766633
# 테스트세트의 R2 : 0.702814782084018
# 릿지
ridge = Ridge().fit(X_train ,y_train)
print('훈련세트의 R2 : ', ridge.score(X_train, y_train))
print('테스트세트의 R2 : ', ridge.score(X_test, y_test))
# 훈련세트의 R2 : 0.6874675811766633
# 테스트세트의 R2 : 0.7028147827762304
# 라쏘
lasso = Lasso().fit(X_train, y_train)
print('훈련세트의 R2 : ', lasso.score(X_train, y_train))
print('테스트세트의 R2 : ', lasso.score(X_test, y_test))
print('학습에 사용한 특성 개수 : ', np.sum(lasso.coef_ != 0))
# 훈련세트의 R2 : 0.6874675569356257
# 테스트세트의 R2 : 0.7028388999869983
# 학습에 사용한 특성 개수 : 1👀 세개 모두 큰 차이가 없음을 알 수 있다.
📉 다중회귀
독립변수 2개 이상, 독립변수 바꿔가면서 R2 제일 높게 만들기
🐼 우리조 🥰 3조(1등) 🥰 결과
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
X = df[['displacement', 'horsepower',
'weight', 'model year', 'origin']]
y = df[['mpg']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=7)
lr = LinearRegression().fit(X_train, y_train)
print('---선형---')
print('훈련 세트의 R2 : ', lr.score(X_train, y_train))
print('테스트 세트의 R2 : ', lr.score(X_test, y_test))
ridge = Ridge().fit(X_train, y_train) # alpha = 1.0 (default)
print('---릿지---')
print('훈련 세트의 R2 : ', ridge.score(X_train, y_train))
print('테스트 세트의 R2 : ', ridge.score(X_test, y_test))
lasso = Lasso(0.1).fit(X_train, y_train)
print('---라쏘---')
print('훈련 세트의 R2 : ', lasso.score(X_train, y_train))
print('테스트 세트의 R2 : ', lasso.score(X_test, y_test))
print('학습에 사용한 특성 개수 : ', np.sum(lasso.coef_ != 0))👀 결과
---선형---
훈련 세트의 R2 : 0.8202021408042256
테스트 세트의 R2 : 0.8152030073228198
---릿지---
훈련 세트의 R2 : 0.8202007909511442
테스트 세트의 R2 : 0.8152751817620537
---라쏘---
훈련 세트의 R2 : 0.8197225759310358
테스트 세트의 R2 : 0.8159755711957566
학습에 사용한 특성 개수 : 5
🧑🏻💻 교수님 코드
- 'origin'을 원핫인코딩으로 표현
df['origin'].unique()
# array([1, 3, 2])
onehot_origin = pd.get_dummies(df['origin'])
onehot_origin.columns = ['origin1', 'origin2','origin3']- onehot_origin
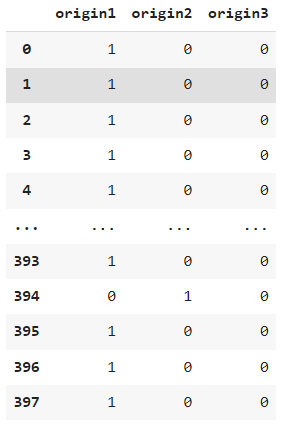
ndf = pd.concat([df, onehot_origin], axis=1)
# 필요없는 기존 컬럼삭제
ndf.drop(['origin'],axis=1, inplace=True)- ndf
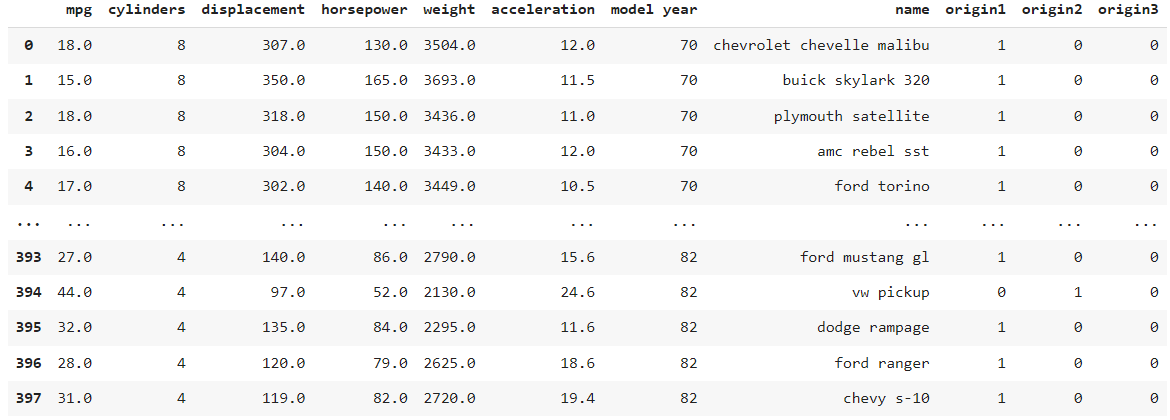
👀 origin이 삭제되고 origin1, origin2, origin3 추가
👩🏻🎓 최적의 alpha값 찾기
Ridge
train_scores = []
test_scores = []
alphas = np.arange(0.0001, 50, 0.001)
# 1~10까지 n_neighbors의 수를 증가 시켜서 학습 후 정확도 저장
for alpha in alphas:
# 모델 생성 및 학습
# print(alpha)
ridge = Ridge(alpha=alpha).fit(X_train, y_train)
# 훈련 세트 정확도 저장
train_scores.append(ridge.score(X_train, y_train))
# 테스트 세트 정확도 저장
test_scores.append(ridge.score(X_test, y_test))
plt.figure(dpi=100)
plt.plot(alphas, train_scores, label='훈련 정확도')
plt.plot(alphas, test_scores, label='테스트 정확도')
plt.ylabel('정확도')
plt.xlabel('alphas 수')
plt.legend()
plt.show()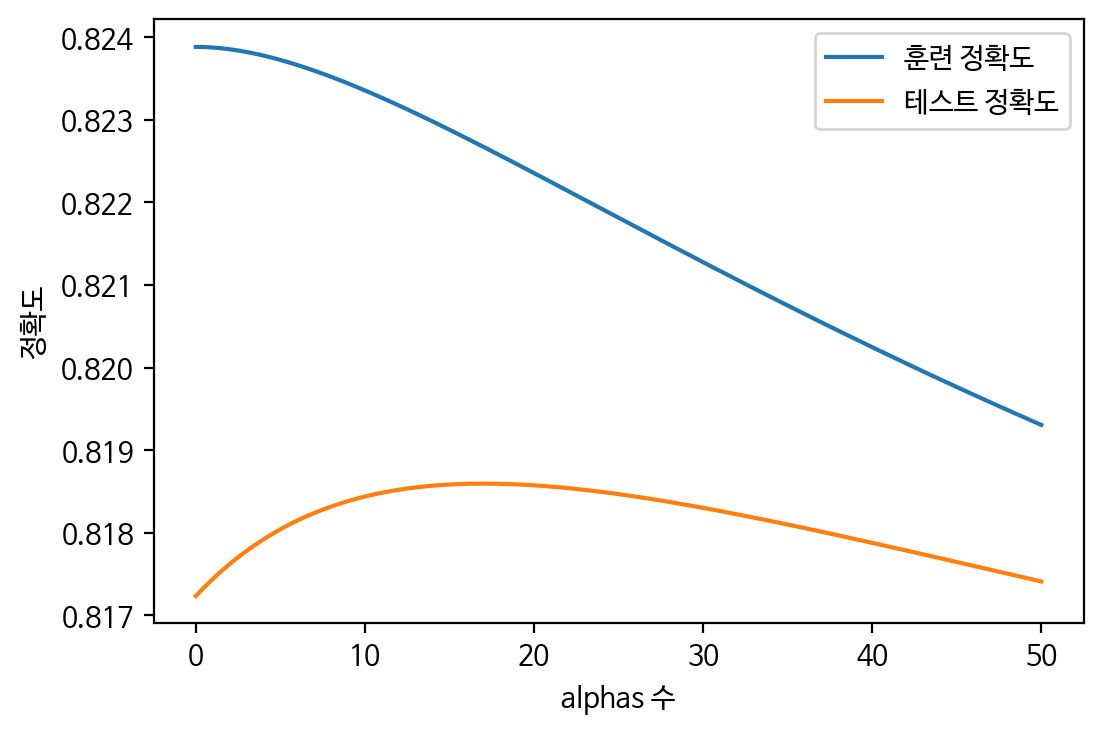
👀 test_scores의 최고점의 인덱스 찾기
max(test_scores) : 0.8185951547484284
test_scores.index(max(test_scores)) : 17002
alphas[17002] : 17.0021
Lasso
train_scores = []
test_scores = []
alphas = np.arange(0.0001, 1, 0.001)
for alpha in alphas:
# 모델 생성 및 학습
# print(alpha)
lasso = Lasso(alpha=alpha).fit(X_train, y_train)
# 훈련 세트 정확도 저장
train_scores.append(lasso.score(X_train, y_train))
# 테스트 세트 정확도 저장
test_scores.append(lasso.score(X_test, y_test))
plt.figure(dpi=100)
plt.plot(alphas, train_scores, label='훈련 정확도')
plt.plot(alphas, test_scores, label='테스트 정확도')
plt.ylabel('정확도')
plt.xlabel('alphas 수')
plt.legend()
plt.show()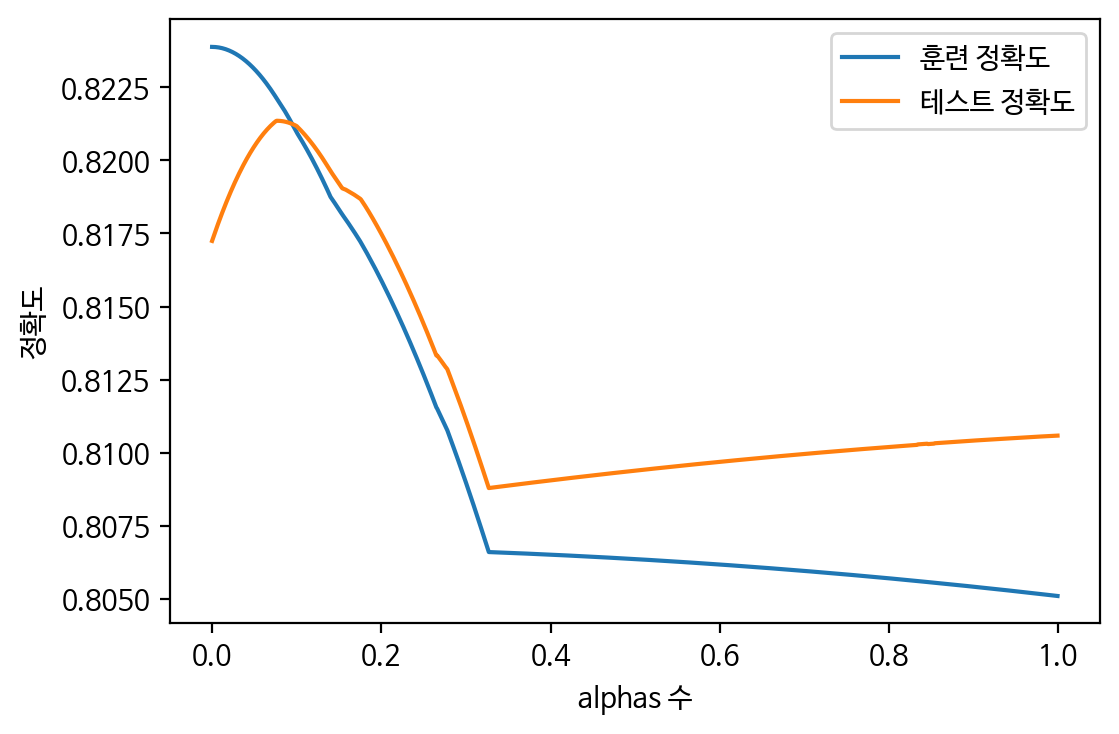
👀 test_scores의 최고점의 인덱스 찾기
test_scores.index(max(test_scores)) : 77
alphas[77] : 0.0771
# 독립변수 9개
X = ndf[['cylinders','displacement','horsepower','acceleration','origin1','origin2','origin3','model year','weight']]
y = ndf['mpg']
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=7)
from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(X_train, y_train)
print('---선형---')
print('훈련 세트의 R2 : ', lr.score(X_train, y_train))
print('테스트 세트의 R2 : ', lr.score(X_test, y_test))
from sklearn.linear_model import Ridge
ridge = Ridge(17.0021).fit(X_train, y_train) # alpha = 1.0 (default)
print('---릿지---')
print('훈련 세트의 R2 : ', ridge.score(X_train, y_train))
print('테스트 세트의 R2 : ', ridge.score(X_test, y_test))
from sklearn.linear_model import Lasso
lasso = Lasso(0.0771).fit(X_train, y_train)
print('---라쏘---')
print('훈련 세트의 R2 : ', lasso.score(X_train, y_train))
print('테스트 세트의 R2 : ', lasso.score(X_test, y_test))
print('학습에 사용한 특성 개수 : ', np.sum(lasso.coef_ != 0))👀 결과
---선형---
훈련 세트의 R2 : 0.8238799845068281
테스트 세트의 R2 : 0.8172353047461415
---릿지---
훈련 세트의 R2 : 0.8226712408486319
테스트 세트의 R2 : 0.8185951547484284
---라쏘---
훈련 세트의 R2 : 0.8220935705882155
테스트 세트의 R2 : 0.8213537307749026
학습에 사용한 특성 개수 : 7
👀 R2가 높음을 볼 수 있다. Cylinders 또한 원핫인코딩으로 표현하면 더 높아진다.
cylinders 원핫인코딩 결과
- 위와 같은 과정을 똑같이 수행하여 코드 실행