이 포스트의 내용은 Qiskit Textbook | Multiple Qubits and Entanglement - More Circuit Identities을 통해 공부한 흔적임을 밝힙니다.

기본 블록들로 유용한 양자 회로를 구축하고 싶지만 때로는 원하는 기본 블록이 없을 수 있다.
그런 의미에서 기본 게이트를 다른 게이트로 변환하는 방법을 살펴보고
보다 더 복잡하지만 여전히 기본 게이트인 녀석을 구성하는 방법을 알아보자.

먼저 실습에 필요한 패키지들을 준비한다.

from qiskit import QuantumCircuit
from qiskit.circuit import Gate
from math import pi
qc = QuantumCircuit(2)
c = 0 # q_0을 Control로 사용하겠다
t = 1 # q_1을 Target으로 사용하겠다

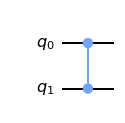
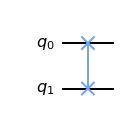
CNOT 게이트로 제어된 Z 게이트 만들기

제어된 Z 게이트는 잘 알려진 2 큐비트 게이트 중 하나다.
CNOT 게이트가 컨트롤이 $|1\rangle$인 경우에만 타겟에 X를 적용하듯
제어된 Z 게이트는 컨트롤이 $|1\rangle$인 경우에만 타겟에 Z를 적용한다.

코드 상에서는 다음과 같이 작성하여 제어된 Z 게이트를 사용할 수 있다.

qc.cz(c, t)
qc.draw()

그런데 IBM Q 디바이스가 제공하는 2 큐비트 게이트는 CNOT뿐이다.
따라서 IBM Circuit Composer에서는 제어된 Z 게이트를 제공하지 않으며
제어된 Z 게이트가 필요하다면 CNOT 게이트를 사용한 게이트로 만들어 사용해야 한다.

그 방법은 아주 간단하다.
단일 큐비트 게이트에서 이야기했듯이 H 게이트를 사용하면 $|0\rangle$과 $|1\rangle$을 각각 $|+\rangle$과 $|-\rangle$로 변환할 수 있다.
그리고 Z 게이트는 $|+\rangle$과 $|-\rangle$에 대하여 X가 $|0\rangle$과 $|1\rangle$에 하는 것과 동일한 작업을 한다.
따라서 행렬 연산을 통해 다음과 같은 항등식을 구할 수 있다.

이것은 제어된 게이트에서도 마찬가지로 작용한다.
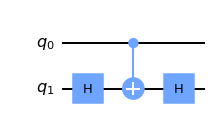
CNOT 게이트를 제어된 Z 게이트로 만들기 위해서는 단지
H 게이트를 CNOT 게이트의 타겟 큐비트 앞뒤에 붙이기만 하면 된다.

qc = QuantumCircuit(2)
qc.h(t)
qc.cx(c,t)
qc.h(t)
qc.draw()

// 이런 구조를 처음 봤을 땐 "게이트 뒤에 H를 붙이는 게 의미가 있나?" 싶었는데
// 이제 보니 이게 위상 반동이 일어나는 거구나...싶다.

보다 일반화하자면, CNOT 게이트 앞뒤에 적절한 회전을 넣음으로써
어떤 회전 게이트든 제어된 버전의 게이트를 만들 수 있다.
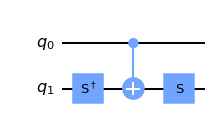
예를 들어, 제어된 Y 게이트를 만들고 싶다면,

qc = QuantumCircuit(2)
qc.sdg(t)
qc.cx(c, t)
qc.s(t)
qc.draw()

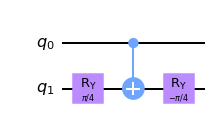
그리고 제어된 H 게이트를 만들고 싶다면,

qc = QuantumCircuit(2)
qc.ry(pi/4, t)
qc.cx(c, t)
qc.ry(-pi/4, t)
qc.draw()

큐비트 뒤바꾸기

두 개의 큐비트의 상태를 서로 뒤바꾸는 작업에 대해 알아보겠다.

# 뒤바꿀 큐비트를 각각 a, b라고 하겠다
a = 0
b = 1

때로는 어떤 값의 정보를 다른 곳으로 이동시켜야 할 때가 있다.
어떤 양자 컴퓨터는 그것을 물리적으로 이동시킬 것이고, 아니면 단지 두 큐비트의 상태만 이동시킬 것이다.
단지 두 큐비트의 상태만 이동시키는 것은 SWAP 게이트를 통해 수행할 수 있다.

qc = QuantumCircuit(2)
qc.swap(a, b)
qc.draw()

이렇게 SWAP 게이트를 직접 사용할 수도 있지만 기본 게이트를 조합해서 만들 수도 있다.

qc = QuantumCircuit(2)
qc.cx(a,b)
qc.cx(b,a)
qc.cx(a,b)
qc.draw()

X 게이트를 통해 $a$와 $b$에 적절한 값을 설정하고 다음을 실행하면
$a$와 $b$가 뒤바뀌는 것을 확인할 수 있다.

from qiskit import Aer, execute
from qiskit.visualization import plot_histogram
backend = Aer.get_backend('statevector_simulator')
results = execute(qc, backend).result().get_counts()
plot_histogram(results)

제어된 회전 Controlled Rotations

Z 게이트는 $z$축을 기준으로 $\pi$만큼 회전시키는 게이트다.
이러한 Z 게이트의 제어된 버전을 CNOT 게이트를 통해 구현하는 방법을 앞에서 살펴 보았다.
같은 맥락에서 다른 제어된 회전 게이트를 구성하는 방법을 알아보자.

먼저 $y$축을 기준으로 회전하는 게이트의 제어된 버전을 고려해보자.

qc = QuantumCircuit(2)
theta = pi
qc.ry(theta/2,t)
qc.cx(c,t)
qc.ry(-theta/2,t)
qc.cx(c,t)
qc.draw()

이것은 컨트롤이 $|0\rangle$이라면 theta/2만큼 회전했다가 다시 -theta/2만큼 회전하여
결국 아무 일도 없던 것처럼 돌아온다.
반면 컨트롤이 $|1\rangle$이라면 두번째 회전 방향을 뒤집어 theta/2만큼 두 번 회전하게 되고
결과적으로는 theta만큼 회전한 효과가 있다.
이것은 $y$축이 $x$축과 직교하기 때문에 가능한 것이다.

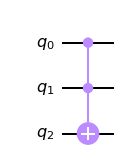
토폴리 The Toffoli

컨트롤이 두 개인 CNOT 게이트는 토폴리 게이트라고 불리며
두 개의 컨트롤이 모두 $|1\rangle$일 경우에만 X 게이트가 적용된다.
이걸 입력값에 따라 AND 게이트 또는 NAND 게이트 역할을 하도록 할 수 있다.
컨트롤이 두 개 있다고 하여 controlled-controlled-NOT, CCX 게이트라고도 한다.

qc = QuantumCircuit(3)
a = 0
b = 1
t = 2

qc.ccx(a,b,t)
qc.draw()

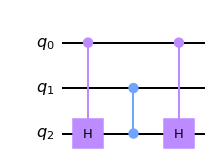
토폴리 게이트는 AND 연산을 위한 유일한 방법은 아니다.
예를 들어, 다음과 같은 회로도 AND 연산을 수행한다.

qc = QuantumCircuit(3)
qc.ch(a,t)
qc.cz(b,t)
qc.ch(a,t)
qc.draw()

H 게이트와 T 게이트의 임의 회전

현재 장치의 큐비트는 온도, 표유 자기장, 인접 큐비트 등으로 인한 노이즈의 영향을 받는다.
양자 컴퓨터의 응용 프로그램 규모가 커질수록 노이즈로부터 큐비트를 보호할 수 있어야 한다.
따라서 게이트를 실수가 발생하기 어렵도록 구현할 필요가 있다.
정확도에는 한계가 있으며 회로가 커질 경우 허용 가능한 오차를 넘어설 것이다.

음... 이 부분에 대해서는 나중에 여유가 될 때 다시 돌아오도록 하자......ㅎ
라기 보다, 음... 사전지식이 너무 부족함을 느낀다.
이 분야는... 여유가 되고 흥미를 되찾았을 때 돌아오도록 하겠다.