[논문 공부] PointNet

IxxI·2023년 1월 8일

3D Vision PointNet paper-review

Abstract

Point Cloud란?
1. 3D 공간을 나타내고자 할때 사용을 하는 기하학적인 구조물이라고 할 수 있다.
2. 일반적으로 point cloud 를 사용해서 연구를 하는 등의 과정을 위해서는 정육면체 모양의 voxel grid로 변형을 한다거나 collection of images로 바꾸어 주는 전처리 과정이 선행 되어 왔다. (여기서 collection of image란 다양한 view의 이미지로 바꾸어 준다는 뜻이다.)
하지만, 본 논문에서는 directly consumes the point cloud라고 한다. 이를 위해서는 입력 point의 permutation invariance를 보존하면서 모델이 point cloud를 process할 수 있도록 한다.

Deep learning on 3D Data
1. 3D point cloud를 voxelized shape으로 바꾸어서 3D convolution을 수행하는 경우가 있는데, 이런 경우에는 보통 sparse한 point에 비해서 연산량이 너무 증가하기 때문에 비효율적이다.
  
  →이를 보완하기 위해서 sparse convolution을 사용하기도 한다. (값이 없는 voxel에 대해서는 연산을 선택적으로 하지 않음)
2. 3D point cloud → 2D Image → 2D CNN을 수행하는 방법도 있다. 하지만 이렇게 하면 space classification은 할 수 있어도 point classification이나 space reconstruction등의 task는 불가능하다.
3. 3D Point cloud → manifold mesh로 형태를 바꾸는 경우도 있는데 일반적으로 non-isometric shape에 대해서는 mesh를 사용하는것이 어렵다.
  
  → 2D로 펼쳐질 수 있는 3D 형태는 모든 normal vector이 한 방향을 가리킨다는 의미이다.
  
  → 그리고 3D processing이나 mesh transformation을 위해서는 manifold mesh를 만들어야 한다. (non-manifold는 실제로 존재하지 않는 형태이기 때문이다.)
Deep learning on unordered sets
1. point cloud는 다른 이미지나 비디오 데이터 구조처럼 순서가 있지 않고 오히려 정렬이 되어 있지 않은 벡터들로 이루어져 있다.
2. 따라서 기존의 CNN이나 RNN등을 적용하기가 어렵다는 문제가 있다.

Deep Learning on Point Sets

1. Point set의 특징

Unordered
- 이미지를 구성하는 픽셀 행렬이나 3차원의 voxel grid와 달리 point cloud는 앞서 언급했던것과 같이 특별한 순서가 없다.
- 즉, 만약에 N개의 3D point를 입력으로 받고 연산을 수행해야 하는 모델이라면 N! 개의 순서 변화에 대해서 모두 동일하게 동작할수 있어야 한다.
Interaction among points
- 비록 3차원 공간에서 point들이 떨어져 있지만 독립적인게 아니라 이웃하는 point들은 meaningful subset를 구성한다.
- 따라서 모델이 가까이 있는 point들의 local structure과 combinatorial interaction을 학습해야 한다.
Invariance under transformations

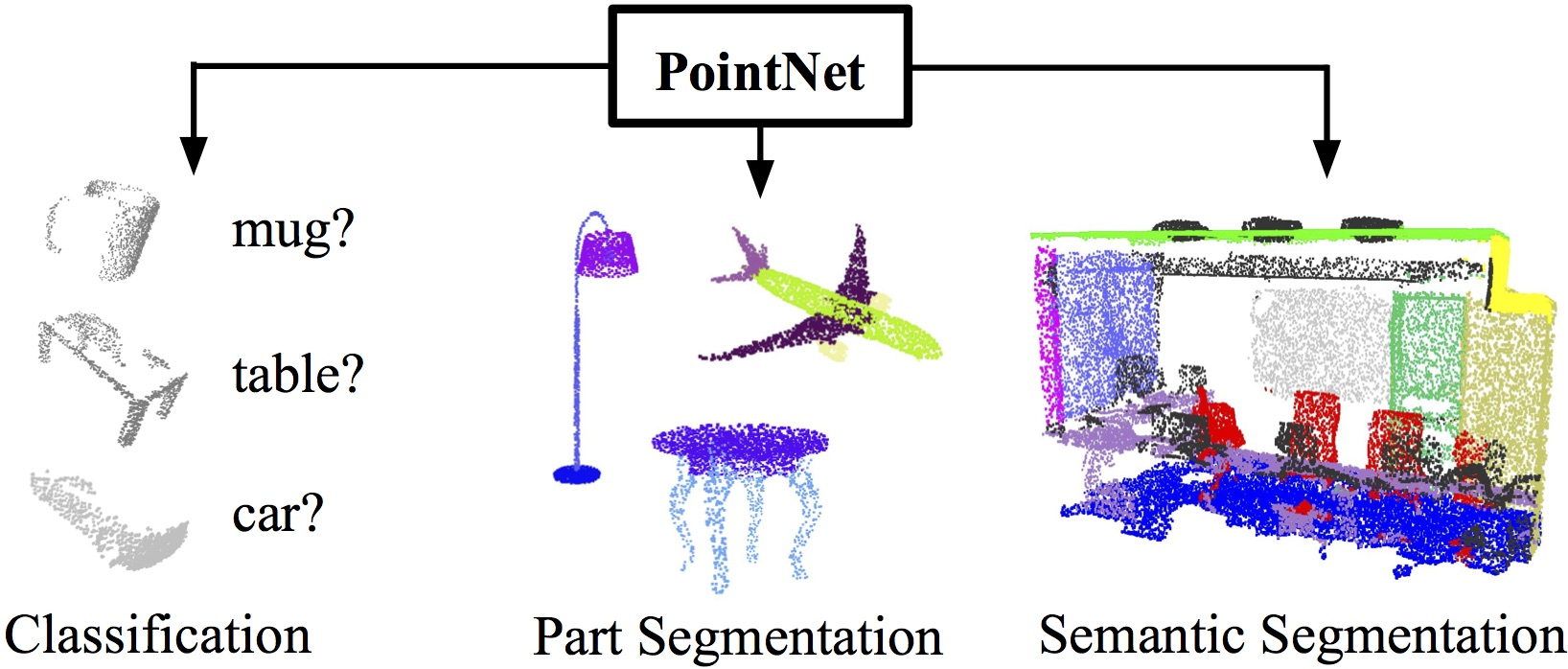
2. Point Net Architecture

Symmetry function for Unordered Input

→ 이 시도는 N개의 point들의 순서가 바뀌는 경우에도 모델의 output은 동일하도록 하기 위함이다.

1. 기존 시도들
    - `RNN`과 같이 sequential data를 다루기 위한 모델을 사용하기에 point cloud의 데이터 개수가 너무 많다.
    - 직접 sorting을 할수 있으면 좋겠으나 sorting이 가능하단 것은 3차원의 point들을 1차원으로 매핑할수 있는 일대일 대응함수가 존재한단 뜻이기 떄문에 현실적으로 불가능하다.
2. 논문의 시도: transformed element에 symmetric function을 적용하기

=> g 함수와 h 함수를 사용해서 최종적인 f 함수를 만들 수 있게 된다.

논문에서는 g로는 Max Pooling을, h로는 Multi Layer Perceptron을 사용한다.
MLP의 경우에는 가중치가 다양할 것이기 때문에 결과적으로 다양한 transformation을 가능하게 할 수 있다고 생각한다.
따라서 point set의 서로 다른 characteristic을 찾을 수 있는 function f를 h, g로 근사해서 얻을 수 있다는 것이다.

Local and Global Information Aggregation

→ 앞선 max pool 과 MLP를 사용하는 모듈의 출력은 각각의 point set마다 feature vector로 나타낸 것을 의미한다. (아마도 초기의 input point cloud들을 그룹화 하여서 각각의 그룹의 feature vector을 나타낸 것으로 확인이 된다)
- 중요한 것은 point segmentation을 위해서는 global, local information이 모두 필요하다는 것이다.
- segmentation에서는 이웃 point와의 관계, local feature이 매우 중요하다.
- 결과적으로 앞서 f 함수로 구한 global feature vector이 global information이고, MLP를 거치기 전의 각 point마다의 feature이 local information이다.
→ 이를 통해서 네트워크는 local geometry와 global semantics에 의존한다.

실험 결과를 보면 per-point normal에 대한 예측의 정확도가 높은것이 point의 local 이웃의 정보를 효과적으로 summarize할 수 있음을 확인 가능하다.
Joint Alignment Network

→ T-net이라는 네트워크를 통해서 affine transformation matrix를 예측한다.
- 다만, T-Net은 전체 네트워크와 거의 동일한 구조를 갖는다. point wise로 feature extract를 하고, Max Pool → Fully Connected Layer을 거친다.
- 근데 만약에 feature 공간 자체에 transformation을 적용하기 위한 matrix를 예측한다면 너무 차원이 커져서 학습할때 수렴이 어려워질 것이다. 따라서 feature transformation matrix가 orthognal matrix와 비슷해지도록 손실함수에 regularize 항을 추가한다.
  - 아무래도 orthogonal matrix라면 입력의 정보를 잃지 않을 것이기 때문이라고 한다. ⇒ 어떻게 orthogonal matrix가 feature preserve에 도움을 준다고 할 수 있을까??