[딥러닝] 퍼셉트론 동작

결정 직선

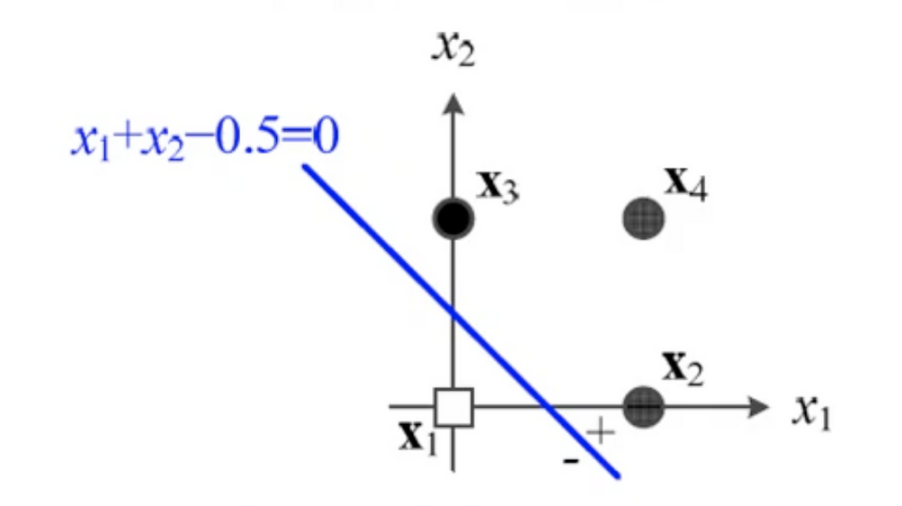
• 입력값x 와 가중치w 를 연산하는 식 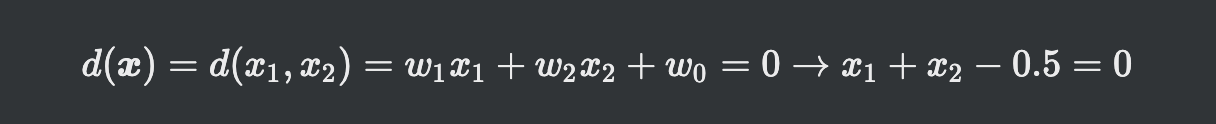직선의 방정식으로 표현됨

• 위 사진처럼 입력값의 분포 어딘가에 생기는 직선으로 안쪽은 - ,바깥쪽은 + 로 분류 됨

• 2차원: 결정 직선, 3차원: 결정 평면, 4차원 이상: 결정 초평면

• 하지만 입력값이 딱 떨어지게 구역을 나눠서 위치하지 않음

학습

수백만개 샘플이 존재할때 분류를 어떻게 할것인가

목적함수

매개변수를 모아놓은 집합 w

또 다른 표현식

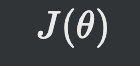매개변수에 의한 결과와 실제 y값의 오차를 담은 함수

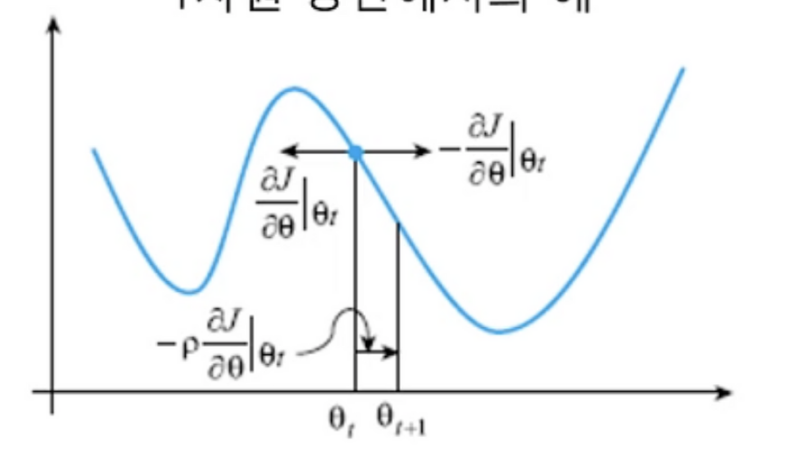매개변수에 의한 J의 변화량(미분) 값을 살펴보고 J값이 가장 작은 부분으로 매개변수 쎄타가 이동을 하는 식으로 학습이 진행됨
목적함수의 활용 용도가 바로 이것

학습률

그래디언트가 결정되고 그대로 적용(크게)을 하게 되면 최저점으로 이동하는 과정에서 최저점을 그냥 지나치는 오류가 발생

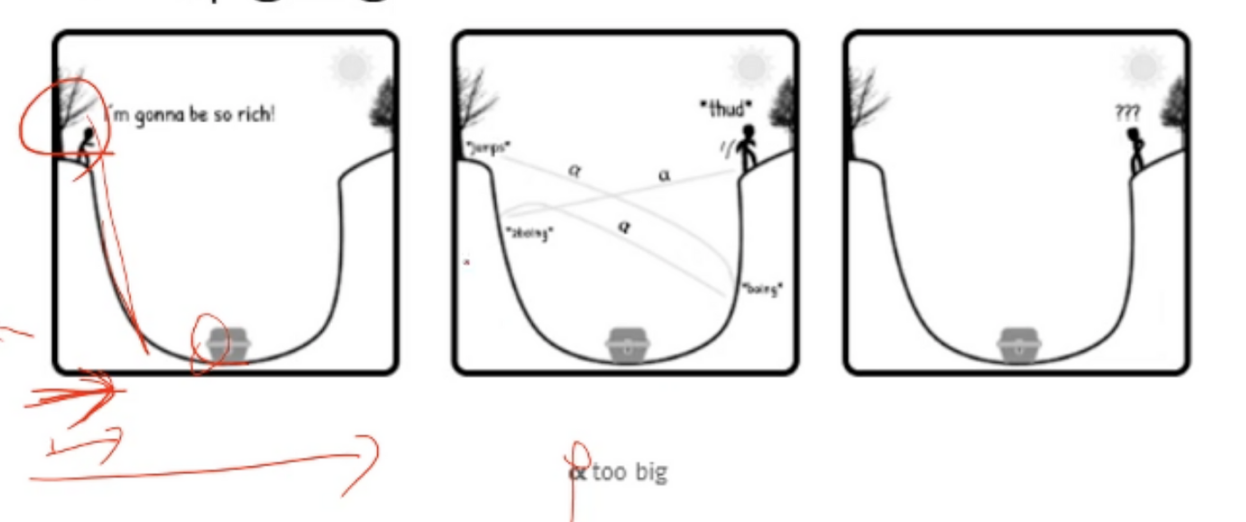
반대로 너무 작게 적용하게 되면 최저점으로 가는 과정에서 로컬 최저점에서 머물게 돼

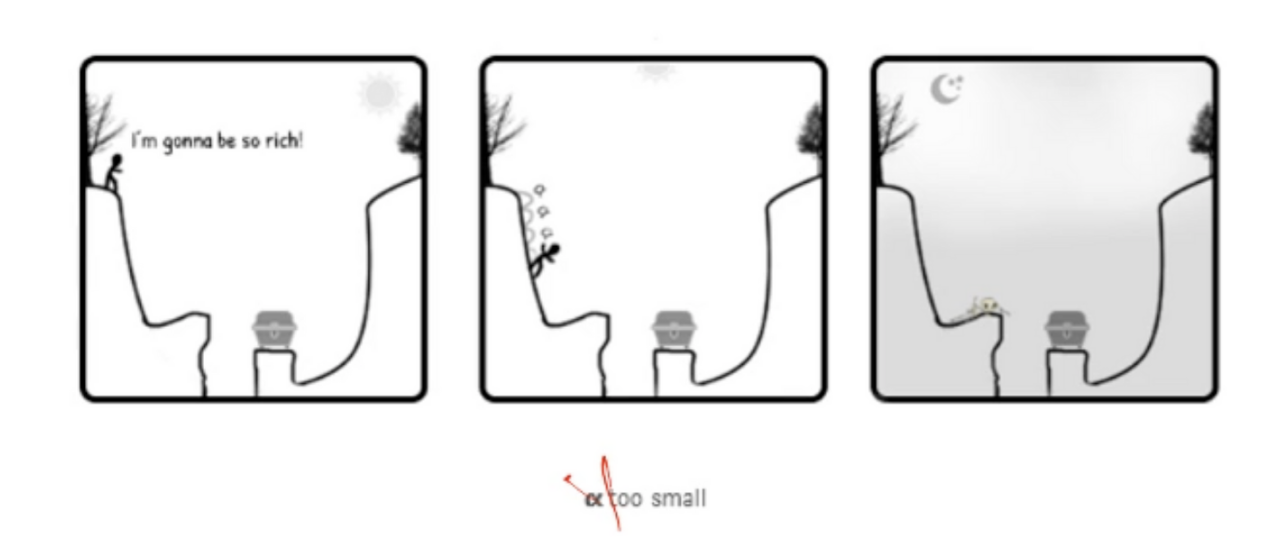
p의 값을 적절하게 조정해서 최저점을 찾아가게 하는 것이 중요