Diffusion Models Beat GANs on Image Synthesis

Hyunsoo Lee·2023년 1월 27일

classifier guidance diffusion paper-review

Generative Model

목록 보기

5/5

GAN 보다 더 높은 quality 의 image 를 생성하는 Diffusion model 의 구조와 Classifier guidance 를 소개한 논문 (Dhariwal & Nichol, 2021)[1] 을 리뷰해 보았다.

수식 번호의 경우 논문의 표기를 따른다.

Abstract

논문에서는 Diffusion model 이 생성 모델에 대한 SOTA 보다 더 좋은 품질의 이미지를 생성함을 보인다. 생성을 위한 더 나은 구조를 찾아 unconditional image generation 을 수행한다. 또한 classifier guidance 를 통해 conditional image generation 역시 수행한다. Classifier 의 gradient 를 이용하는 compute-efficient 방법으로, diversity 와의 trade-off 가 존재한다. 하나의 sample 을 생성하기 위해, BigGAN-deep 에 비해 25번의 iteration 이 더 적게 필요함을 확인하였으며 $128 \times 128$ ImageNet 이미지에 대해 FID score 2.97 을 달성한다. 또한 upsampling diffusion model 과 classifier guidance 를 결합시켜 $256 \times 256$ ImageNet 데이터에 대해 FID score 3.94 를 달성한다.

1. Introduction

Image generation task 에 있어서 GAN 은 지난 몇 년간 SOTA 를 유지해 왔다. 그러나 GAN 을 통해 생성된 sample 들은 diversity 가 높지 않으며, 모델 자체를 학습시키는 과정이 어렵다는 단점 역시 가지고 있다. 따라서 likelihood 를 기반으로 하는 생성 모델들이 제안되었고, 높은 diversity 와 학습이 쉽다는 장점을 가졌지만 이들에 의해 생성된 sample 은 GAN 에 의해 생성된 sample 보다 quality 가 낮았다. 최근에 likelihood 를 이용하는 생성 모델로 diffusion 이 새로 제시되었다. Diffusion 의 training object 는 re-weighted variational lower bound 로, CIFAR-10 데이터셋 생성에 대해서 SOTA 를 달성하였다. 그러나 다른 데이터셋 (LSUN, ImageNet) 에 대해서는 여전히 GAN 보다 좋은 성능을 나타내지 못하였다. Nichol & Dhariwal 에 의해 upsampling stack 이 도입되며 diffusion model 개선이 이루어졌지만, ImageNet 에 대한 SOTA 모델 (BigGAN-deep) 보다 좋지 않은 FID score 를 나타냈다.

이 논문에서는, diffusion model 과 GAN 의 성능이 차이나는 이유를 크게 2가지라고 주장한다.

1) 최신 논문에서 제안된 GAN 은 그 구조가 매우 다양하게 탐색되었으며 많이 개선되어 있다. 반면 Diffusion 은 충분한 모델 구조 개선이 이루어지지 않았다.

2) GAN 은 sample 의 다양성 (diversity) 와 quality 사이의 trade-off 가 이루어진다. 즉 sample 에 대한 전체 distribution 은 cover 하지 않지만, 그 quality 가 좋다.

따라서 논문에서는 diffusion model 의 구조를 개선시키고, diversity 에 대한 trade-off 를 도입해 sample 의 품질을 향상시킨다. 이를 통해 서로 다른 dataset 에 대해, GAN 보다 더 좋은 성능을 기록하고 SOTA 를 갱신한다.

2. Background

💡 2. 절에서는 Diffusion model 의 개요 (DDPM)와 이를 개선시킨 연구들을 소개하고, 실험 환경에 대해 설명한다.

Ho et al. (2020) 에서 처음으로 제안된 DDPM 은 noise $x_T$ 로부터 시작해 ‘denoising’ 과정을 거쳐 sample $x_{T-1}, x_{T-2}, \cdots, x_1, x_0$ 를 생성한다. $x_t$ 에 가해진 noise $\epsilon \sim \mathcal{N}(0, \mathbf{I})$ 를 예측하는 모델 $\epsilon_{\theta}(x_t, t)$ 를

|| \epsilon_{\theta} (x_t, t) - \epsilon || ^2_2

가 최소가 되게끔 학습시킨다. 학습된 network 를 이용해, 분포 $p_{\theta}(x_{t-1} | x_t)$ 를 모델링한다. 분포의 분산 $\Sigma_{\theta}(x_t, t)$ 는 고정된 상수로 두고, 평균 $\mu_{\theta}(x_t, t)$ 는 network $\epsilon_{\theta}(x_t, t)$ 에 대한 식으로 나타낸다. 이로부터, reparameterization trick 을 통해 $x_t$ 로부터 sampling 을 통해 $x_{t-1}$ 을 얻는다.

또한 DDPM 을 VAE 로써 해석해, 더 좋은 성능을 가져다주는 training object $L_{\text{simple}}$ 을 유도한다.

L_{\text{simple}} = \mathbb{E}_{t \sim \text{Uniform}(1, T), \; x_0 \sim q(x_0), \; \epsilon \sim \mathcal{N}(0, \mathbf{I})}[ || \epsilon - \epsilon_{\theta}(x_t, t)||^2_2 ] \tag{26}

DDPM 의 training 과정과 sampling 과정은 Song & Ermon (2021) 에서 제안된 것 처럼 각각

Training : Denoising score matching
Sampling : Annealed Langevin dynamics

를 따른다.

2.1. Improvements[2]

Nichol & Dhariwal (2021) 는 DDPM 에서 고정되어 있었던 분산 $\Sigma_{\theta}(x_t, t)$ 을 매개화 한다. 출력값이 $v$ 인 인공 신경망에 대해 (mixing vector $v$ 를 예측하는 인공 신경망),

\Sigma_{\theta}(x_t, t) = \exp(v \log{\beta_t}+(1-v)\log{\tilde{\beta}_t}) \tag{1}

로 매개화 한다. 이 때 $L_{\text{simple}}$ 은 $\Sigma_{\theta}$ 에 의존하지 않으므로, 두 개의 network ( $\Sigma_{\theta}(x_t, t)$ , $\epsilon_{\theta}(x_t, t)$ )를 모두 학습시키기 위한 새로운 training object

L_{\text{new}}=L_{\text{simple}} + \lambda L_{\text{vlb}}

를 정의한다. $L_{\text{vlb}}$ 는

L_{\text{vlb}} = L_0 + L_1 + \cdots + L_T \tag{22}

이며, $L_{\text{vlb}}$ 내에서 $\epsilon_{\theta}(x_t, t)$ 에 관련된 gradient 는 업데이트를 진행하지 않게끔 해 오직 $\Sigma_{\theta}(x_t, t)$ 만을 update 하도록 한다. 결과적으로 $\Sigma_{\theta}(x_t, t)$ , $\epsilon_{\theta}(x_t, t)$ 는 각각 $L_{\text{vlb}}$ , $L_{\text{simple}}$ 을 통해서 업데이트 되는 것이다. 실제 학습 시에는 $L_{\text{vlb}}$ 에 importance sampling (IS) 을 적용하였다.

이를 통해 sample 의 품질을 크게 하락 시키지 않으며 더 빠른 sampling 이 가능하다. 이 논문에서도, 위 training object 를 이용해 학습을 진행한다.

Song et al. (2020) 에서는 DDIM 이 제안되었다. DDIM 은 DDPM 의 forward process 를 non-Markovian noising process 로 대체한 모델로, DDPM 에 비해 (1번의 sampling 당) 50회 적은 sampling step 을 사용할 수 있다. DDIM 의 forward process 에서 marginal distribution $q(\mathbf{x}_t | \mathbf{x}_0)$ 는 DDPM 과 동일하지만, sampling process 에서 reverse noise distribution 의 분산을 조정함으로써 DDPM 과는 다른 sampling 과정을 유도한다 (deterministic sampling). 분산을 0으로 고정한 것이 DDIM 으로, latent variable 과 image 사이의 deterministic mapping 을 유도하며 더 적은 step 만에 sampling 이 가능하도록 한다.

2.2. Sample Quality Metrics

서로 다른 모델이 생성한 sample 의 quality 를 비교하기 위해 아래와 같은 metric 들을 사용하였다.

Inception Score (IS)

모델이 ImageNet 의 각 class 에 대해 생성한 sample 의 집합이, 전체 class distribution 을 얼마나 잘 나타나는지 정량적으로 측정한다. 단점으로는, 전체 dataset 에 대한 작은 부분집합을 memorize 한 model 이 높은 IS 값을 가지게 된다는 점이다.

Fréchet Inception Distance (FID score)

IS 보다, 인간의 평가와 더 유사한 결과를 나타내는 척도로 알려져 있다. FID는 Inception-V3 latent 공간에서 서로 다른 두 이미지 분포 간의 대칭적인 measure 를 나타낸다. 최근에는 standard pooled feature 보다 spatial feature 를 사용하는 sFID score 가 제안되었다. sFID 는 FID 에 비해 공간 정보 간의 관계를 더욱 잘 capture 하며, 이미지의 분포가 일관적으로 high-level structure 를 따르게끔 한다.

Precision and Recall

Precision 은 모델이 산출한 sample 들 중 data manifold 에 존재하는 비율을 측정하며, Recall 은 sample 들에 의해 형성되는 manifold 에 속하는 data point 의 비율을 측정한다.

cf) 머신러닝에서 사용되는 precision 과 recall 의 정의는 다음과 같다.

\text{Precision} = \frac{\text{TP}}{\text{TP}+\text{FP}}

\text{Recall} = \frac{\text{TP}}{\text{TP}+\text{FN}}

논문에서는 diversity 와 sample 의 품질을 동시에 정량적으로 측정 및 비교하기 위해, FID score 를 기본 metric 으로 사용한다. 추가적으로 Quality 측정을 위해 precision 과 IS 를, diversity 를 측정하기 위해 recall 을 사용한다.

3. Architecture Improvements

💡 3. 절에서는 FID score 를 향상시키기 위한 모델 구조에 대해 설명한다.

Diffusion model 에 대해 가장 좋은 quality 의 sample 을 추출하는 모델 구조를 탐색하였다.

DDPM 이 처음 제안된 Ho et al. (2020) 에서는, Jolicoeur-Martineau et al. (2020) 에서 denoising score matching 을 사용할 때 sample 의 품질을 높이기 위해 제안한 U-Net 구조를 사용한다. U-Net 구조를 요약하면 다음과 같다.

Residual layer 와 downsampling layer 를 연속적으로 사용
Residual layer 와 upsampling convolution 역시 연속적으로 적용
위 layer 들 간 Skip-connection 을 적용
각 residual block 에 대해, global attention 을 적용 (# of attention head = 1, resolution $16 \times 16$ ) 하고 timestep embedding 의 projection 을 추가

위 구조에 다음과 같은 변형을 추가하여 $128 \times 128$ size 의 ImageNet 에 대해 sample 의 diversity 와 quality 를 높였다.

Model size 는 일정하게 유지하면서, width 대비 depth 를 증가시키기
Number of attention head 증가
Attention 의 resolution 으로 $32 \times 32$ , $16 \times 16$ , $8 \times 8$ 사용
Residual connection 의 scale 을 모두 $\frac{1}{\sqrt{2}}$ 배
Upsampling / downsampling 과정에서 BigGAN 의 residual block 을 사용

모델은 $128 \times 128$ ImageNet 데이터셋에 대해 학습시켰으며, batch size = 256, sampling step = 250 으로 두었다. 여러가지 모델 구조에 대해 학습을 진행하며 FID score 를 측정하였다. 그 결과는 Table 1. 에 나타나 있다.

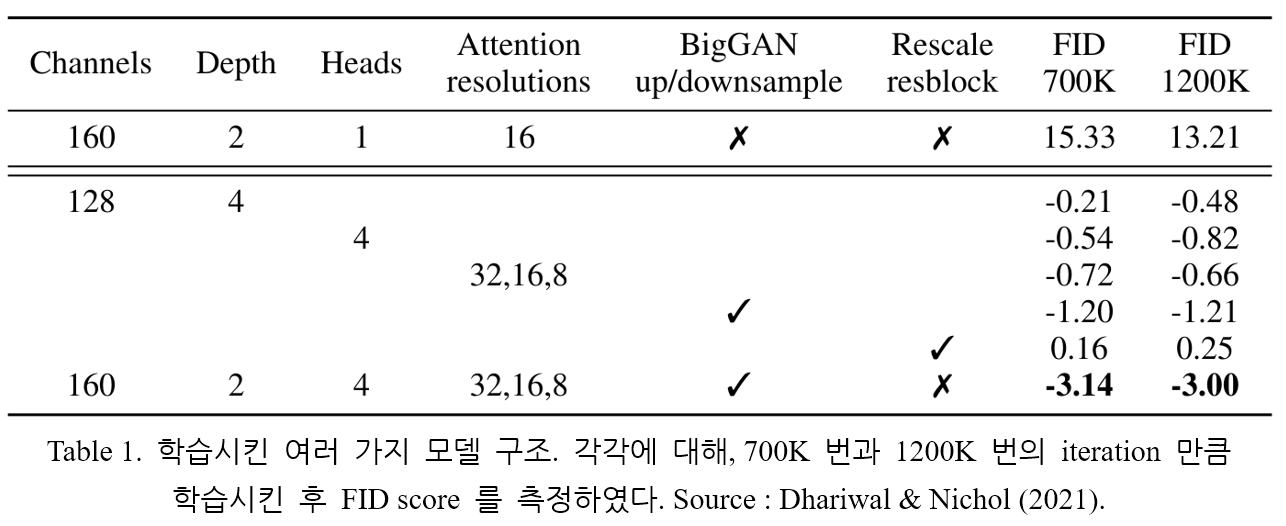
Residual connection 에 대한 rescaling 외의 모든 기법은 성능을 향상시켰고, 복합적으로 좋은 효과를 가져왔다. Figure 2. (Left) 에 나타나 있듯, 모델의 depth 증가할수록 성능 역시 높아졌다. 그러나 학습에 소요되는 시간 역시 증가하고, width 가 더 큰 모델과 동일한 성능을 달성하기까지의 시간 역시 더 많이 소요되었다. 결과적으로 이후 실험에서는, depth 를 변화시키며 성능을 측정하지는 않았다.

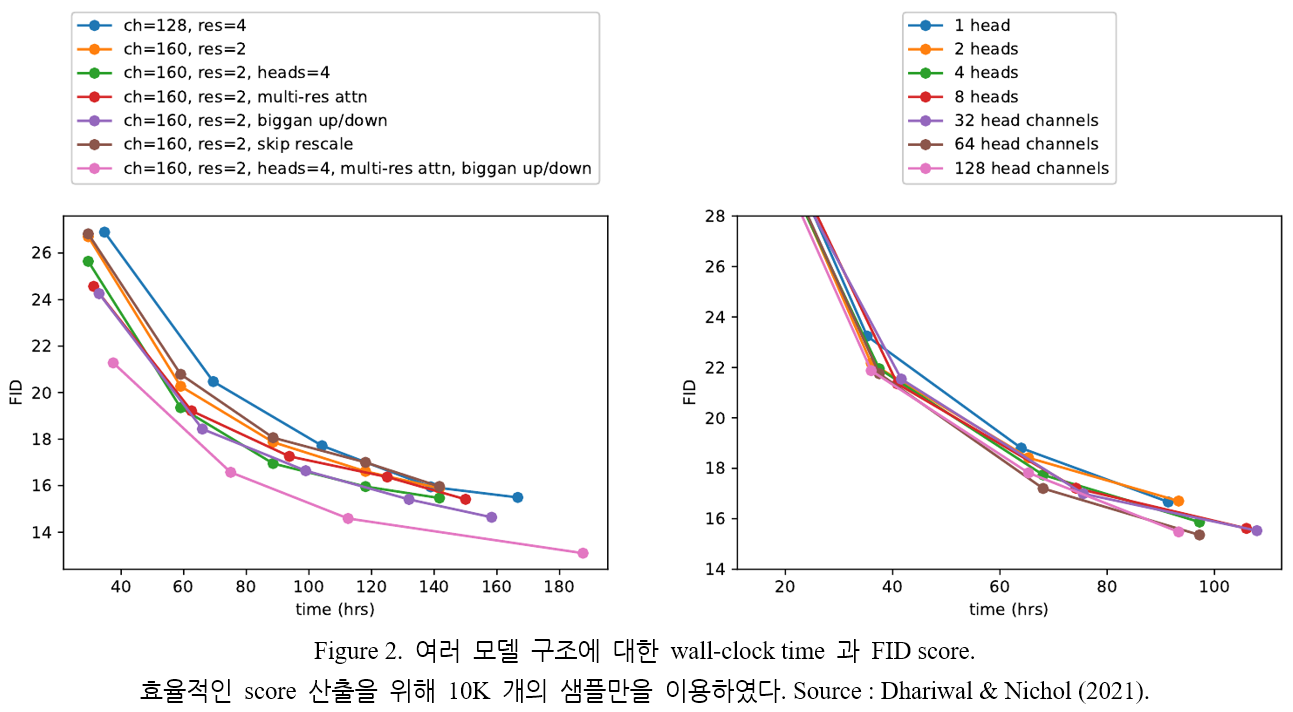
논문에서는 Transformer 구조에서 제안된 attention 과 더 잘 일치하는 attention 구조에 대한 탐색 역시 진행하였다. Attention head 의 수 또는 하나의 head 에 존재하는 channel 의 수를 변화시키며 FID score 를 측정하였다. 변화시킨 조건 외에는 base channel 수는 128개, residual block 은 2개 (1개의 resolution 당)를 사용하였으며 multi-resolution attention, BigGAN up/downsampling 을 적용하였다. Table 2. 에 실험 결과가 나타나 있다. Head 의 수를 늘리거나 채널의 수를 줄이는 것이 높은 성능을 유도하는 것을 알 수 있다.

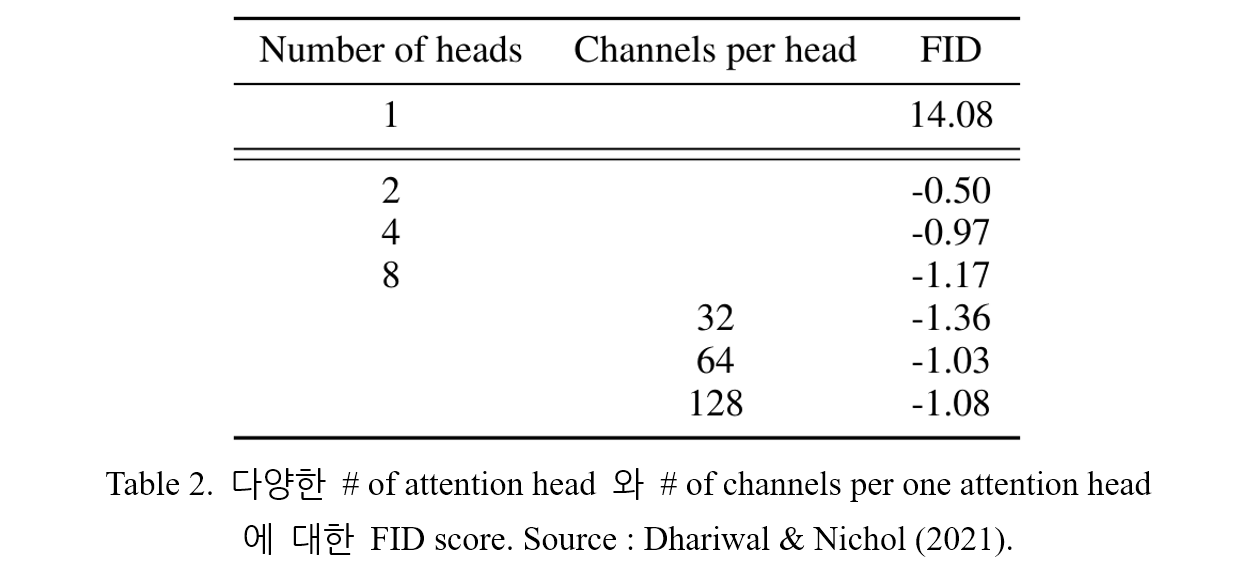
Figure 2. (Right) 에서 알 수 있듯, 64 channel 을 사용하는 경우 시간적인 측면에서 가장 좋은 결과를 나타냈으므로, 이후 실험에서는 64개 채널을 기본으로 사용하였다. 이러한 선택은 최근에 제안된 transformer 구조와 잘 일치하며, 비슷한 FID score 값을 가진다.

3.1. Adaptive Group Normalization (AdaGN)

AdaGN 은 group normalization 이 적용된 후, 각각의 residual block 에 대해 timestep 및 class embedding 을 추가한다. 과정을 수식으로 나타내면 아래와 같다. Timestep 및 class embedding 에 대한 linear projection 을 각각 $y_s, y_b$ 라 하고, residual block 내에서 convolution 이 한 번 적용되었을 때의 값을 $h$ 라고 하면,

\text{AdaGN}(h, y) = y_s \cdot \text{GroupNorm}(h) + y_b

Table 3. 에 AdaGN 의 사용 유무에 따른 성능을 나타내었다. AdaGN 이 적용되었을 때 모델의 성능이 더 좋음을 확인할 수 있다.

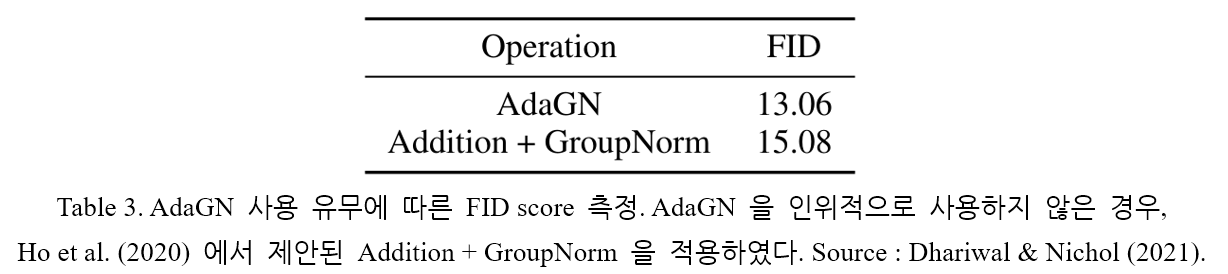
따라서 앞으로의 실험에서는 기본적으로 AdaGN 을 적용시켰다.

모델에서 최종적으로 사용한 구조는 다음과 같다.

2 residual blocks per resolution
Multiple heads with 64 channels/head
32, 16, 8 attention resolution
BigGAN up/downsampling
AdaGN

4. Classifier Guidance

GAN 의 경우 특정 class 에 속하는 이미지를 생성하기 위해 class label 을 사용한다. 대부분의 경우 discriminator 가 특정 class 에 이미지가 속하는지 분류하는 classifier $p(y|x)$ 처럼 설계되어 class-conditional normalization 기법을 사용한다. GAN 의 특징으로부터, class label 에 conditional 한 diffusion 역시 설계할 수 있다. 3.1. 절에 제시된 것 처럼, 이미 정규화 층에는 class 에 대한 정보를 포함시켰다 ( $y_b$ ). 논문에서는, 이와는 또 다른 방법을 도입한다. Diffusion generator 자체를 원하는 방향으로 변화시킬 수 있게 해 주는 classifier $p(y|x)$ 를 고려해 보자. Class label $y$ 에 속하는 이미지를 생성하도록 하기 위해, noise 가 가해진 이미지 $x_t$ 에 대한 classifier $p_{\phi}(y|x_t, t)$ 를 학습시키고 gradient $\nabla_{x_t} \log{p_{\phi}(y|x_t, t)}$ 를 이용해 sampling process 가 특정 class 의 이미지를 생성하도록 조정할 수 있다.

4 절에서는 classifier 를 도입하는 이론적인 방식 2가지에 대해 논의한다. 이후, 실제 sampling 과정에서 (in-practice) 적용될 수 있게끔 변형시키는 방법을 소개한다. Notation 의 경우 편의를 위해

p_{\phi}(y|x_t) := p_{\phi}(y|x_t, t) \\ \epsilon_{\theta}(x_t) :=\epsilon_{\theta}(x_t, t)

로 표기한다.

4.1. Conditional Reverse Noising Process

Unconditional diffusion model 은 sampling 과정에서 $p_{\theta}(x_t | x_{t+1})$ 을 사용한다. 이를 class label $y$ 에 conditional 하게 바꾼다면, sampling 의 각 step 이 아래 확률분포로부터 sample 을 추출하게끔 하면 충분하다. Normalizing 상수를 $Z$ 라고 하면,

p_{\theta, \phi}(x_t | x_{t+1}, y) = Zp_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t) \tag{2}

식 (2)로부터 sampling algorithm 을 유도해 보자. 기존 diffusion model 의 $p_{\theta}$ 를 간소화 시켜 나타내면

p_{\theta}(x_t | x_{t+1}) = \mathcal{N}(\mu, \Sigma) \tag{3}

이고 이 분포로부터 reparameterization trick 을 사용해 sampling 을 진행했었다. 여기서, Class-conditional 특성을 도입하려면 $p_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t)$ 의 값을 계산해야 한다. 계산의 편의성을 위해 $\log{p_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t)}$ 를 계산하고 log 를 다시 지우는 방식을 생각해 보자. 우선,

\log{p_{\theta}(x_t | x_{t+1})} = -\frac{1}{2}(x_t - \mu)^{\top} \Sigma^{-1} (x_t - \mu) + C \tag{4}

를 계산할 수 있다.

$\log{p_{\phi}(y|x_t)}$ 의 curvature 가 $\Sigma^{-1}$ 에 비해 작다고 가정하자. 이 가정은 diffusion step 의 수가 무한히 발산하지 않을 때 성립한다. 가정이 성립한다면, $x_t =\mu$ 근방에서의 테일러 전개에 의해

\log{p_{\phi}(y|x_t)} \simeq \log{p_{\phi}(y|x_t)}|_{x_t = \mu} + (x_t - \mu) \nabla_{x_t}\log{p_{\phi}(y|x_t)}|_{x_t = \mu} \tag{5}

식 (5)에서 $\log{p_{\phi}(y|x_t)}|_{x_t = \mu}$ 는 상수이고, $\nabla_{x_t}\log{p_{\phi}(y|x_t)}|_{x_t = \mu} =:g$ 로 치환하면

\log{p_{\phi}(y|x_t)} \simeq (x_t - \mu)g + C_1 \tag{6}

이 성립한다. 식 (4), (6) 을 이용해 $\log{p_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t)}$ 를 계산해 보면

\log{p_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t)} = -\frac{1}{2} (x_t - \mu - \Sigma g)^{\top} \Sigma^{-1} (x_t - \mu - \Sigma g) + C \tag{9}

식 (9)에 reparameterization trick 을 적용하면 $z \sim \mathcal{N}(\mu+\Sigma g, \Sigma)$ 에 대해

\log{p_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t)} = \log{p(z)} + C \tag{10}

이 성립한다. 이제 식 (10)에서 log 를 지우는 과정을 생각하면,

p(z) = p_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t)\cdot \exp(C) :=Z p_{\theta}(x_t | x_{t+1}) p_{\phi} (y | x_t) = p_{\theta, \phi}(x_t | x_{t+1}, y)

이다. 결과적으로 분포 $\mathcal{N}(\mu+\Sigma g, \Sigma)$ 로 부터 $z$ 를 추출하는 것이 sampling 과정에 해당하게 된다. 상수 $C$ 의 경우, 식 (2)에서 normalizing constant $Z$ 로 고려되었다.

즉, 식 (10)으로부터 conditional transition operator 는 평균값이 변한 unconditional transition operator 로 근사 될 수 있음을 알 수 있다. 이를 적용한 sampling algorithm 은 아래와 같다.

4.2. Conditional Sampling for DDIM

4.1. 절의 방법은 stochastic sampling 과정에서만 적용될 수 있다. DDIM 과 같은 deterministic sampling 에는 적용될 수 없으며, 따라서 score-based trick 을 새롭게 소개한다. 데이터에 추가되는 noise 를 예측하는 network 를 $\epsilon_{\theta}(x_t)$ 라고 해 보자. Notaion 은 Ho et al. (2020) 을 따른다. Perturbed data distribution $q(x_t)$ 에 대한 score function 을 계산하면

\nabla_{x_t} \log{q(x_t)} = -\frac{\epsilon_{\theta}(x_t)}{\sqrt{1-\bar{\alpha}_t}} \tag{11}

과 같다. 이에 대한 유도 과정은 다음과 같다.[2]

DDPM 에서

s_{\theta}(x_t, t) \simeq \nabla_{x_t}\log(q(x_t)) = \mathbb{E}_q(x_0)[\nabla_{x_t} \log{q(x_t | x_0)}]

이다. 이 때 아래 두 식이 성립하므로

q(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1-\bar{\alpha}_t) I)

x_0 = \frac{1}{\bar{\alpha}_t}(x_t - \sqrt{1-\bar{\alpha}_t} \epsilon_{\theta}(x)t))

Distribution $q$ 의 pdf 식에 이를 대입해 계산하면

s_{\theta}(x_t, t) = - \frac{\epsilon_{\theta}(x_t, t)}{\sqrt{1-\bar{\alpha}_t}}

이다.

Class-conditional 조건을 위해 다음 분포 $q(x_t, y)=q(x_t)q(y|x_t)$ 를 고려해 보자. 앞서 정의한 classifier $p_{\phi}(y|x_t)$ 를 이용해 이에 대한 score function 을 구하면

\nabla_{x_t} \log{q(x_t)q(y|x_t)} = - \frac{\epsilon_{\theta}(x_t, t)}{\sqrt{1-\bar{\alpha}_t}} + \nabla_{x_t} \log{p_{\phi}(y|x_t)} \tag{13}

이제 joint distribution 의 score 를 이용해 network 를 update 시키는 과정을 생각하자. 식 (13)을 통해 update 하고자 하는 network 를 $\hat{\epsilon}(x_t)$ 라고 하자. 식 (11) 과 유사하게

\nabla_{x_t} \log{q(x_t)q(y|x_t)} = -\frac{\hat{\epsilon}_{\theta}(x_t)}{\sqrt{1-\bar{\alpha}_t}}

가 성립하고 따라서

\hat{\epsilon}(x_t) := \epsilon_{\theta}(x_t) - \sqrt{1-\bar{\alpha}_t} \nabla_{x_t} \log{p_{\phi}(y|x_t)} \tag{14}

로 정의할 수 있다. DDIM 과 동일한 sampling 과정을 사용할 수 있지만 $x_t$ 로부터 $x_{t-1}$ 을 sampling 하는 식 내의 $\epsilon_{\theta}$ network 가 $\hat{\epsilon}$ network 로 바뀌게 된다. 이에 대한 알고리즘은 아래와 같다.

4.3. Scaling Classifier Gradients

Generation task 에 classifier 를 적용하기 위해서는 우선 ImageNet 데이터에 대해 classifier 를 학습시킨다. 모델 구조의 경우 U-Net 을 기본적으로 사용하며 $8 \times 8$ size 의 layer 를 downsampling 시켜 분류 문제를 해결하게끔 변형하였다. Diffusion model 에서 사용한 noise 와 동일한 분포에 대해 classifier 를 학습시켰고 과적합 방지를 위해 randomcrop augmentation 역시 적용하였다. 학습이 종료된 후에는 식 (10)을 이용해 diffusion 모델과 classifier 를 결합시켰다.

그러나 실제 실험에서는, classifier 에 의한 gradient 를 1보다 비율로 scaling 시켜 주어야 함을 발견하였다. Scale = 1 을 사용한 경우 class 에 할당된 확률이 50% 근처로 계산되었고 생성된 sample 들은 해당 class 에 속하지 않은 경우가 많았다. 반면 1보다 큰 scale factor 를 사용한 경우 특정 class 에 속할 확률이 100% 부근의 값으로 계산되었고 올바른 sample 들이 생성되었다.

Scaling 의 효과는 다음 수식으로부터 설명될 수 있다 : 임의의 상수 $C$ 에 대해,

s \cdot \nabla_x \log{p(y|x)} = \nabla_x \log{\left(\frac{1}{C}p(y|x)^s \right)}

가 성립한다. Classifier distribution 이 $p(y|x)^s$ 에 비례하게끔 re-normalize 된 classifier 로부터 conditioning 이 일어나게 된다. $s>1$ 일 경우 분포 $p(y|x)$ 가 더 sharp 해 지게 되고, 이는 해당되는 class 에 대한 gradient scale 을 증가시킨다. 결과적으로 확률분포가 특정 class 에 대해 높아지고 나머지 class 에 대해서는 낮아지기 때문에 sample 의 diversity 는 낮아지지만 fidelity (quality; 품질) 가 높아지게 된다.

지금까지는, 사용하는 diffusion model 은 unconditional model 이라고 가정하였다. 그러나, diffusion model 자체를 conditional model 로 사용할 수도 있다. Classifier guidance 는 동일한 방식으로 적용된다. 모델의 종류와 classifier guidance 유무에 따른 sampling 결과를 Table 4. 에 나타내었다. Conditional model 과 guidance 를 같이 사용함으로써 가장 좋은 FID score 를 얻을 수 있다.

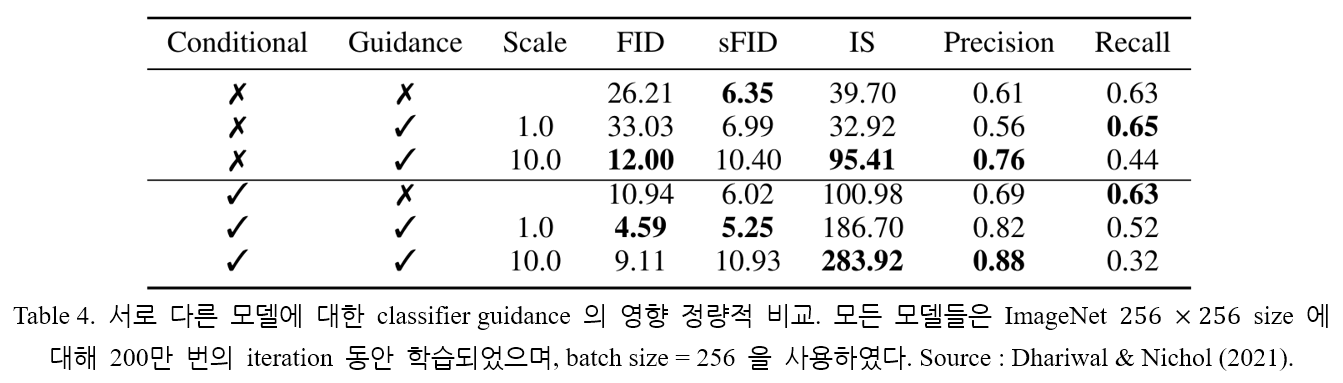
2.2. 절에서 소개한 여러 가지 metric 을 살펴보자. Recall 은 diversity 를, Precision 과 IS 는 quality 를, FID 와 sFID 는 둘을 종합적으로 고려한 지표이다. Table 4. 로부터 sample quality 와 diversity 사이의 trade-off 를 관찰할 수 있다. Gradient scale 을 조정하며 더 구체적으로 trade-off 를 살펴본 결과를 Figure 4. 에 나타내었다.

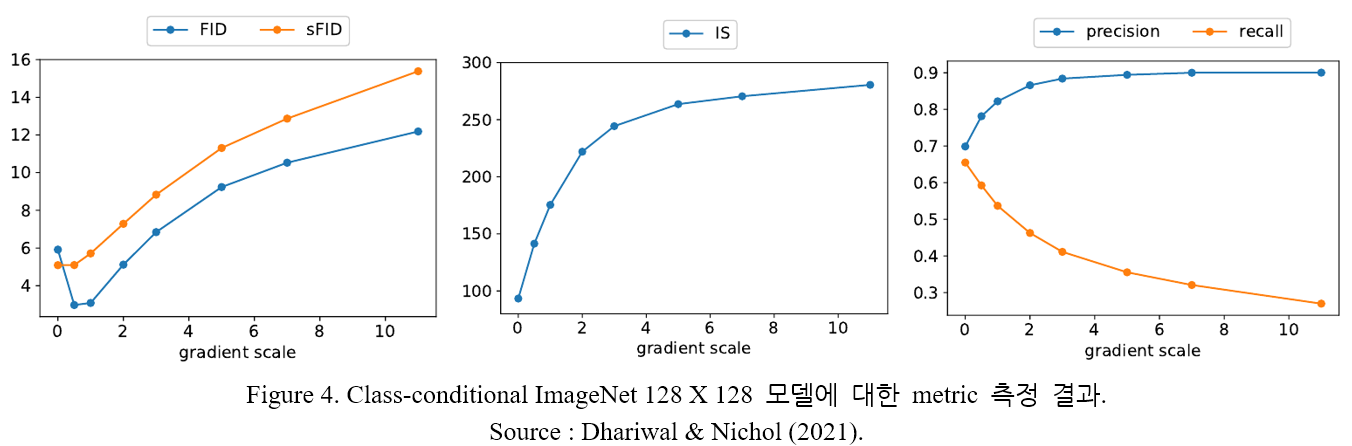
Figure 4. 에서 precision, recall 값을 통해 trade-off 현상을 확인할 수 있다. Gradient scale 이 커질수록 quality (IS, precision) 은 증가하는 반면 diversity (recall) 은 감소한다. FID, sFID score 는 이 둘을 종합적으로 고려하므로 중간 지점 ( $s=1$ 부근) 에서 가장 좋은 결과를 가짐을 알 수 있다.

Figure 5. 는 classifier guidance 와 BigGAN-deep 의 performance 를 정량적으로 비교한다.

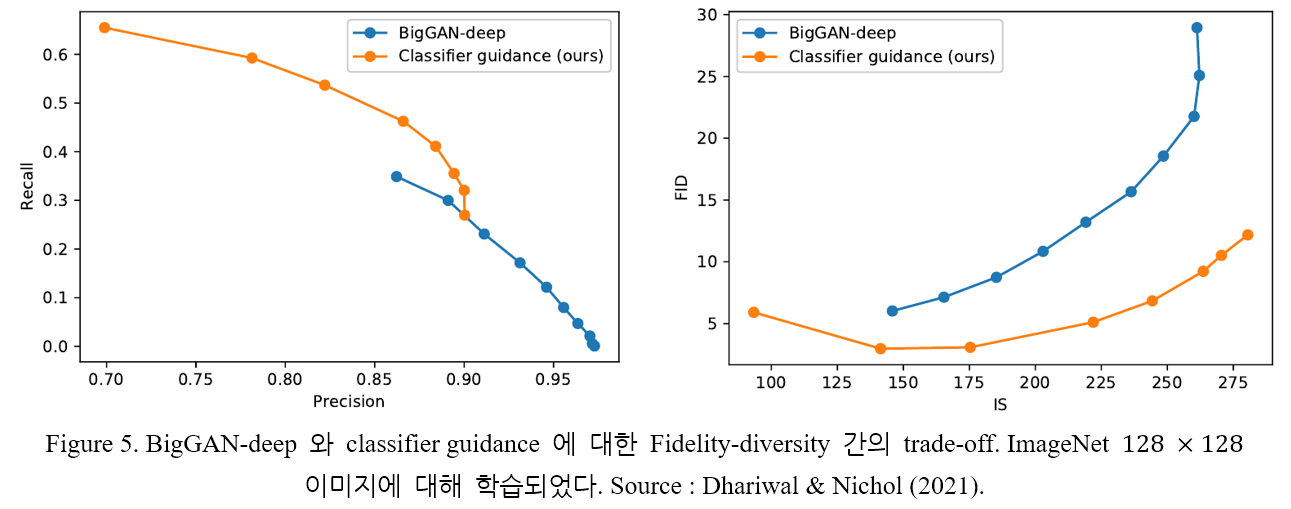
BigGAN-deep 보다 classifier guidance 의 FID score 가 더 좋음을 알 수 있다.

5. Results

첫 번째로 개선시킨 모델 구조를 test 하기 위해 LSUN 데이터셋 중 bedroom, horse, cat class 에 대해 모델을 학습시켰다. 두 번째로 classifier guidance 의 효과를 검증하기 위해 ImageNet dataset ( $128 \times 128, 256 \times 256, 512 \times 512$ ) 에 대해 학습을 진행하였다.

5.1. SOTA Image Synthesis

모델 (ADM : Ablated Diffusion Model 이라고 표기한다)의 결과는 Table 5. 에 나타나 있다. 모든 task 에 대해 가장 좋은 FID score 를 달성하며, 1개의 task 를 제외하고 가장 좋은 sFID score 역시 달성한다. 개선된 모델 구조만을 이용해서도 LSUN 데이터셋과 $64 \times 64$ ImageNet 에 대해 SOTA 를 갱신하며, 더 높은 해상도의 ImageNet 데이터에 대해서는 classifier guidance 를 통해 GAN 보다 높은 품질의 이미지를 생성한다. GAN 보다 높은 품질의 이미지를 생성함과 동시에, recall 에 의해 측정되는 diversity 역시 높은 값을 유지한다. 또한 이 과정은 25번의 diffusion step 만을 필요로 한다.

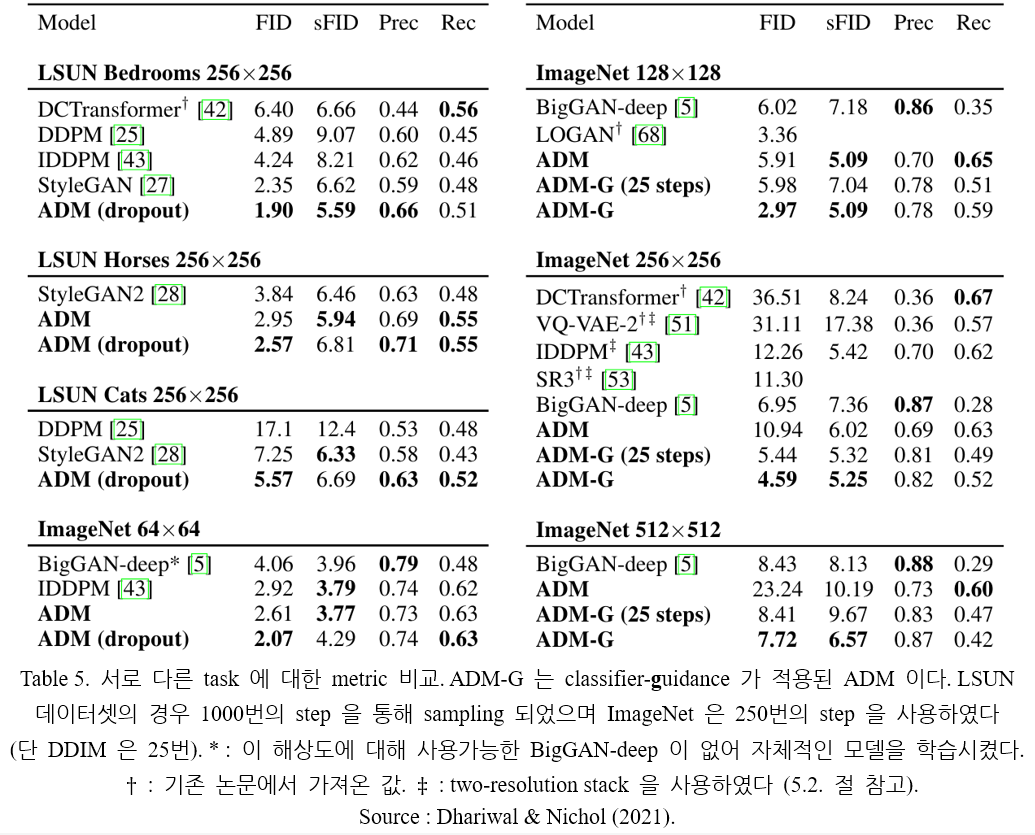
Figure 6. 은 BigGAN-deep 모델과 가장 좋은 성능을 기록한 ADM 에 의해 생성된 이미지를 나타낸다. 이미지의 quality 는 비슷하지만 diffusion 이 더 다양한 이미지를 산출한다.

5.2. Comparison to Upsampling

논문에서는 classifier guidance 의 결과를 two-stage upsampling stack 에 의한 결과와도 비교한다. Nichol and Dhariwal (2021) 과 Saharia et al. (2021) 에서, low-resolution diffusion model 과 upsampling diffusion model 을 결합하여 이미지를 생성하는 방법이 제시되었다 (two-stage). Low-resolution model 은 sample (image)를 생성하고, upsampling model 은 해당 sample 에 대해 upsampling 을 수행한다. 이 기법을 통해 ImageNet $256 \times 256$ image 에 대한 FID score 를 개선시켰지만, BigGAN-deep 만큼의 quality 를 얻지는 못하였다.

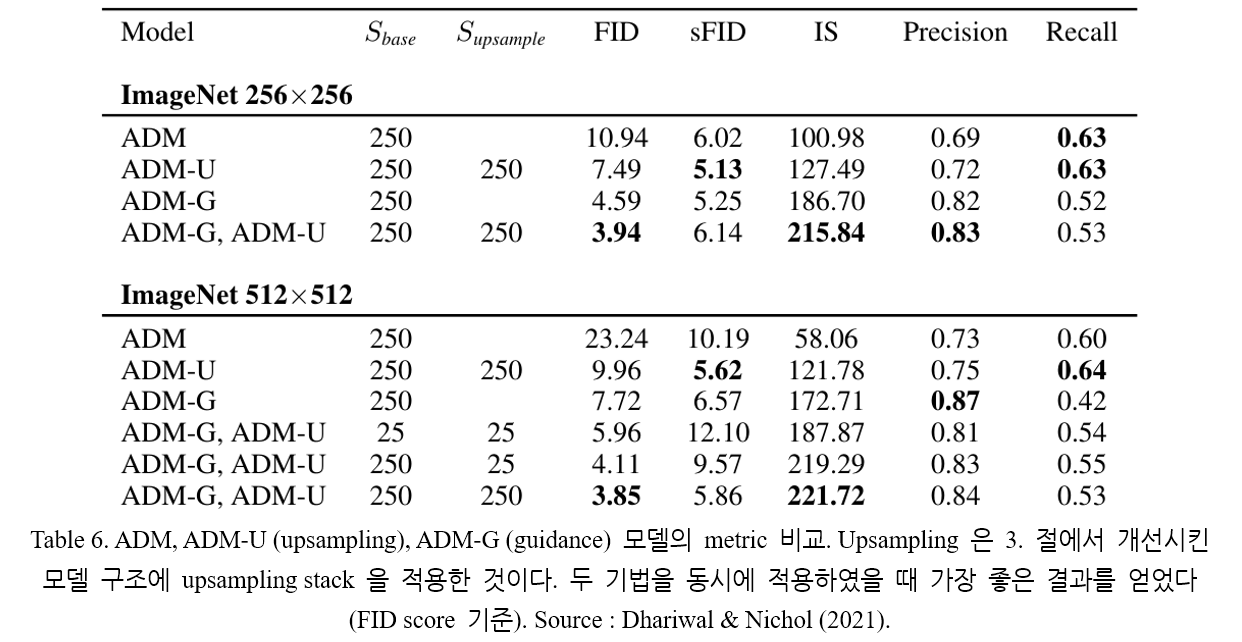
Table 6. 에는 guidance 와 upsampling 이 서로 다른 metric 에 대해 좋은 값을 나타낸다는 점이 나타난다. Upsampling 의 경우 높은 recall 값을 유지하며 precision 을 개선시키고, guidance 는 앞서 설명한 trade-off 를 유도한다. 두 기법을 동시에 사용해 가장 좋은 FID score (3.85) 를 얻었는데, low-resolution model 에 guidance 를 적용시키고 upsampling model 을 통과시킨 경우이다.

Reference

[1] Prafulla Dhariwal, Alex Nichol, Diffusion Models Beat GANs on Image Synthesis, CVPR, arXiv:2105.05233, 2021.

[2] Lilian Weng, “What are Diffusion Models?", 2021.07.11.

Hyunsoo Lee

이전 포스트