Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise

Hyunsoo Lee·2023년 1월 20일

Generative Model

목록 보기

4/5

기존의 DDPM 에서 사용한 degradation 방식은 이미지에 Gaussian noise 를 추가하는 것이다. 이를 일반화해, noise 를 사용하지 않고 임의의 변환 (arbitrary transformation)을 사용해 이미지를 degrade 시키는 방식을 제안한 Cold Diffusion 논문 (Bansal et al., 2022)을 리뷰해 보았다.

Abstract

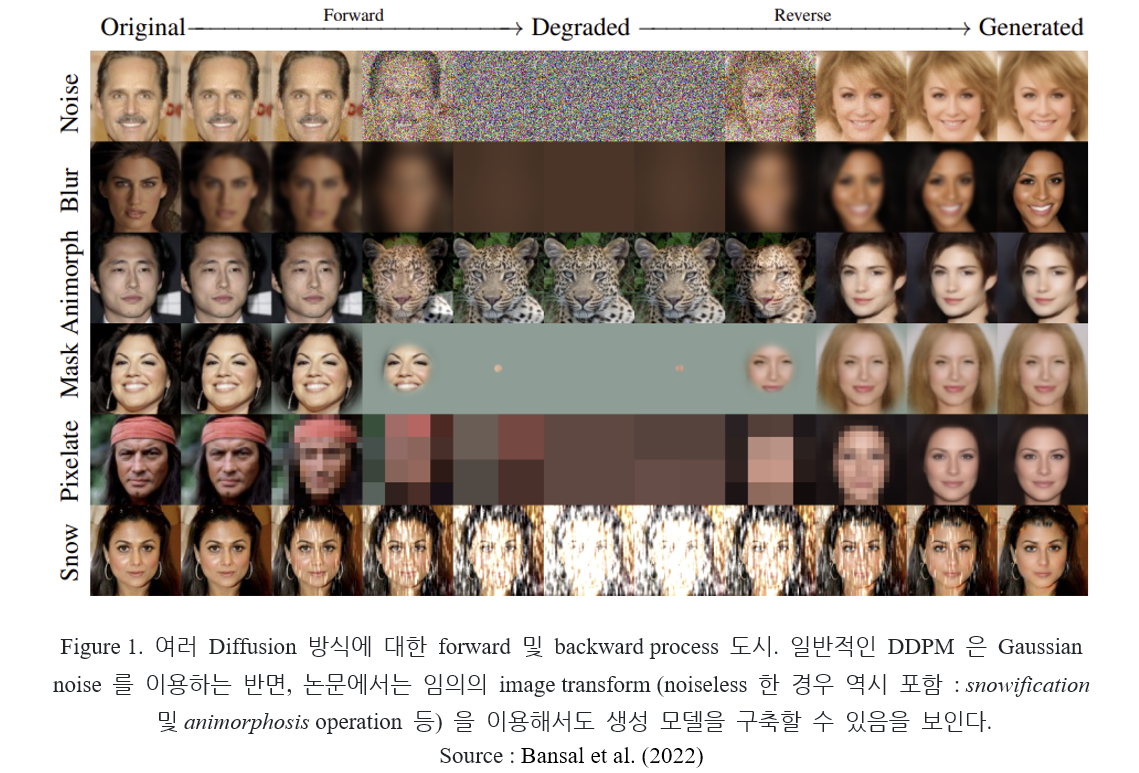
Ho et al. (2020) 에서 제안된 DDPM 에서 적용된 image transformation (degradation) 은 Gaussian noise 를 추가하는 것이다. 그러나, diffusion model 은 image degradation 의 방식에 상관없이 작동하며, 여러 degradation 방식이 적용될 수 있다. Blur, masking 과 같은 방식이 적용될 수 있으며 이가 적용된 diffusion model 이 일반화되어 생성 모델을 만든다. Arbitrary process 에 대한 inverse 과정을 포함하는 diffusion model 의 일반화 결과를 얻을 수 있다.

1. Introduction

Diffusion model 은 generative modeling 에 있어서 좋은 성능을 나타내며, 대부분의 경우 다음 과정을 따른다.

Training : Random Gaussian noise 가 가해진 image 에 대해 denoised image 를 산출하는 denoising network 를 학습시킨다.
Test : 학습시킨 denoising network 를 통해 pure gaussian noise 를 image 로 변환한다. Noise step 을 따라 gaussian noise 를 추가하고 denoising network 를 적용한다.

Diffusion 은 Langevin dynamics 를 이용하는 sampling 과정으로도 볼 수 있다. High temperature (noise 가 많은 상태) 로 부터 시작해, noise 가 적은 cold state 로 변환하는 과정을 포함한다. 또한, variational inference 를 사용하는 denoising network 를 학습시키는 관점으로도 볼 수 있다.

논문에서는 diffusion model 에 사용되는 gaussian noise 의 필요성에 대해 논하며, 고전적인 DDPM 이 따르는 이론에서 벗어난, generalized diffusion models 를 제안한다. Gaussian noise 를 이용한다는 제약점을 넘어, blurring, downsampling 과 같은 임의의 image transformation 을 이용해 만들어진 모델을 고려한다. 이 변환을 inverse 하는 신경망을 학습시켜, photo-realistic image 를 생성해 내는 기법에 대해 연구한다.

학습 및 테스트 과정에 있어서 gaussian noise 를 필요로 하지 않는 cold diffusion 을 통해 고전적인 DDPM 에 사용된 이론에 대한 이해를 넓히며, 기존에 제시된 DDPM 과 매우 다른 성질을 나타내는 생성 모델이 만들어질 수 있다는 가능성 또한 연다.

2. Background

Data 에 gaussian noise 를 추가하는 것은 다음과 같은 특성을 가진다.

1) Score matching 과정에서, 데이터 분포에 대한 support 중 low-dimensional manifold 에 존재하는 것들을 ambient space 로 확장시켜 score matching 이 원활하게 일어나게 해 준다.

2) Low density region 에 대한 data augmentation 으로 해석될 수 있다. Langevin dynamics 에서 mode 간의 원활한 mixing 이 일어날 수 있게 해 준다.

논문에서는 diffusion model 에 있어서 noise 가 필수적이지 않으며, 여러 inverse problem 을 해결함에 있어서 noise 를 제거하는 것이 가져오는 영향을 관찰한다.

3. Generalized Diffusion

고전적인 DDPM 은 2가지 구성 요소를 가진다.

1) Image degradation : image 에 gaussian noise 를 추가

2) Restoration : 학습된 restoration operator 를 사용해 denoising

→ Gaussian noise 에 국한되어 있지 않은, 임의의 degradation operation 을 사용하는 generalized diffusion 을 고려한다.

3.1. Model components and training

이미지 $x_0 \in \R^N$ 에 대해, severity $t$ 를 가지는 degradation operator $D$ 를 고려하자. 이 때 $x_0$ 에 대한 degradation 은

x_t = D(x_0, t)

이다. 이 때 $x_t$ 는 $t$ 에 대해 연속이어야 하며, $D(x_0, 0)=x_0$ 가 만족되어야 한다. Ho et al. (2020) 에서 제시된 DDPM 의 $D$ 는 분산이 $t$ 에 비례하는 Gaussian noise 를 추가하는 연산자이다. 이를 일반화 시켜, $D$ 가 blurring, masking, downsampling 과 같은 다른 변환을 수행하는 연산자가 되게 한다.

Restoration operator $R$ 은 $D$ 에 대한 inverse process 를 수행하며, 아래 성질을 만족한다.

R(x_t, t) \simeq x_0

연산자 $R$ 은 $\theta$ 에 대해 매개화된 인공 신경망을 통해 구현된다. Training object 는

\min_{\theta} \mathbb{E}_{x \sim \chi} || R_{\theta}(D(x, t), t)- x||

와 같다. 이 때 $\chi$ 는 data distribution 을 나타내며 $x$ 는 임의의 data point 에 해당된다.

3.2. Sampling from the model

적절한 $D$ 에 대한 $R_{\theta}$ 를 학습시킨 후, 이 연산자를 이용해 degradation 을 invert 시킬 수 있다. 작은 severity $t$ 에 대해서는, $R_{\theta}$ 를 통해 원본 이미지를 one-shot 만에 얻을 수 있다. 그러나 $R_{\theta}$ 가 simple convex loss 를 이용해 학습되었기 때문에, 큰 값의 $t$ 에 대해서는 좋은 결과를 가져다 주지 못한다. DDPM 에서는 image 에 가해지는 noise 의 크기를 점점 감소시키며 denoising operation 을 반복해서 적용한다. 이러한 Naive sampling 의 과정을 나타내면 아래와 같다.

소개된 Algorithm 1. 은 noise 에 기반한 diffusion model 에 잘 적용된다. $R_{\theta}$ 가 gaussian noise 를 제거하게끔 잘 학습될 수 있기 때문이다. 그러나 cold diffusion 에 대해서는 잘 적용되지 않는다 (Figure 2.). 따라서, more smooth and cold degradation 을 이용하는 경우 적용할 수 있는 새로운 Algorithm 2. 를 제시한다. Restoration operator $R_{\theta}$ 가 degradation 을 완벽하게 invert 시키지 못해도, 좋은 reconstruction 을 생성할 수 있는 구조를 가지고 있다.

3.3. Properties of Algorithm 2

$R_{\theta}$ 가 $D$ 에 대한 완벽한 inverse 과정을 나타내는 경우, Algorithm 1, 2 모두 $x_0$ 를 reconstruct 한다. 그렇다면 $R_{\theta}$ 가 완벽하지 않은 경우 (오차를 가지는 경우)를 살펴보자.

작은 값의 $x, s$ 에 대해 Algorithm 2. 는 $R_{\theta}$ 의 오차에 민감하지 않다. 즉 알고리즘의 작동 방식은 어떠한 $R_{\theta}$ 를 선택해도, $R_{\theta}$ 가 $D$ 에 대한 완벽한 inverse 과정을 나타내는 경우와 동일하다. 이를 간단히 증명해 보자.

Proof 벡터 $e$ 에 대한 선형 degradation function

D(x, s) \simeq x+s\cdot e

를 생각해 보자. $x=x_0, s=0$ 에서 $D(x, s)$ 의 테일러 전개가

D(x, s) \simeq x + s \cdot e + \text{H.O.T}

와 같음을 고려하자. $s$ 가 작은 값이므로 위와 같은 1차 근사를 생각할 수 있다. 이 때 테일러 전개 식의 0차항 (상수항)은 0이어야 한다. 앞서 $D$ 에 대한 가정 중

D(x, 0)=x

가 성립하기 때문이다. 이제 임의의 $R_{\theta}$ 에 대해, $\hat{x_0}$ 를 대입하면

x_{s-1} = x_s - D(R_{\theta}(x_s, s) , s) + D(R_{\theta}(x_s, s) , s-1)

$x_s$ 의 정의로부터

x_{s-1} = D(x_0, s) - D(R_{\theta}(x_s, s) , s) + D(R_{\theta}(x_s, s) , s-1)

테일러 전개를 이용하면

x_{s-1} \simeq x_0+s \cdot e - R_{\theta}(x_s, s) - s \cdot e+R_{\theta}(x_s, s) ,+(s-1) \cdot e

식을 정리하면

x_{s-1} = x_0+(s-1) \cdot e = D(x_0, s-1)

즉 $s<t$ 인 모든 $s$ 에 대해 $R_{\theta}$ 의 선택에 상관없이 $x_s$ 를 생성한다. 이로써 알고리즘의 작동 방식은 어떠한 $R_{\theta}$ 를 선택해도, $R_{\theta}$ 가 $D$ 에 대한 완벽한 inverse 과정을 나타내는 경우와 동일함이 증명되었다.

반면 Algorithm 1. 은 이러한 특징을 나타내지 않는다. $R_{\theta}$ 가 $D$ 에 대한 완벽한 inverse 를 나타내지 못할 경우,

x_0 = R_{\theta}(x, 0) \neq D(R(x, 0), 0)

이므로 작은 값의 $s$ 에 대해서도 Algorithm 1. 은 오차가 존재하게 된다.

4. Generalized Diffusions with Various Transformations

다양한 방식의 degradation 을 적용하고 이에 대한 performance 를 측정한다. MNIST, CIFAR-10, CelebA 에 대해 Algorithm 2. 를 이용한다.

4.1. Deblurring

Gaussian blur 를 적용하는 diffusion model 을 생각해 보자. Step $t$ 가 증가할수록 blurred 된 정도는 심해진다. Step $t-1$ 에서 blurring 에 사용된 gaussian kernel 을 $\{G_t \}$ 라고 하면, blurring 과정은 convolution 으로 나타낼 수 있다.

x_t = G_t * x_{t-1} = G_t * \cdots * G_1 * x_0 = \bar{G_t} * x_0 = D(x_0, t)

가 성립한다. 3.1. 절에 제시된 training object 를 이용해 학습을 진행하였으며, Algorithm 2. 를 이용해 sampling 을 진행하였다. 그 결과는 Figure 3. 와 Table 1. 과 같다.

Table 1. 에서, Algorithm 2. 를 이용하는 경우가 direct sampling 보다 더 좋은 (낮은) FID score 값을 가짐을 알 수 있다. 이로부터 일반화된 sampling 기법 (Algorithm 2. 내용)을 통해 실제 데이터 분포에 더 가까운 분포가 학습됨을 알 수 있다.

Blur operator 의 경우, 각 sampling step 에 주파수를 더해 주는 것으로 해석될 수 있다. Sampling 과정에서 나오는 항들 중

D(\hat{x_0}, t)-D(\hat{x_0}, t-1)

는

\bar{G_t} *x_0 - \bar{G}_{t-1}*x_0

와 같고, 이는 band-pass filter 로써 작용해 degradation 과정 (step $t$ )에서 지워진 주파수를 다시 더해주는 역할을 한다.

4.2. Inpainting

이번에는 이미지에서 순차적으로 픽셀들을 흑백화 하는 변환을 생각해 보자. 다음과 같은 Gaussian mask 를 적용한다.

$n\times n$ size의 이미지에 대해 분산이 $\beta$ 인 2D gaussian curve (size $n \times n$ ) 를 정의한다. Peak 의 값이 1이 되게끔 정규화 하고, $1-\text{(mask)}$ 를 대입해 mask 의 중심값 (원래 peak 였던 값)이 0이 되도록 한다. 이렇게 해서 만들어진 mask 를 $z_{\beta}$ 라고 하자.

증가수열 $\beta_i$ 에 대해 $\{ z_{\beta_i}\}$ 를 총 $T$ 번 적용한다고 하자. 픽셀이 지워지는 정도는 $\beta_i$ 의 값을 변경해 조절할 수 있다. Masking 과정을 나타내면

x_t = D(x_0, t) =x_0 \cdot \Pi^t_{i=1}z_{\beta_i}

라고 하자. Sampling 결과는 Figure 4. 와 Table 2. 에 나타나 있다.

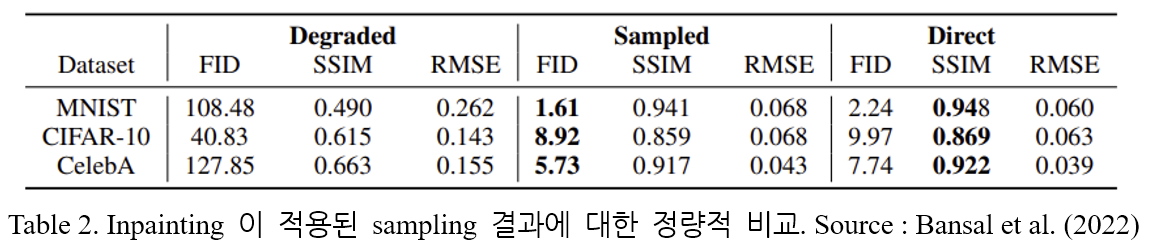
Table 1. 과 마찬가지로, Algorithm 2. 를 이용하는 경우가 direct sampling 보다 SSIM score 는 낮지만 더 좋은 FID score 값을 가진다.

4.3. Super-Resolution

이번에는 매 step 마다 $n \times n$ size 의 image 를 $\frac{n}{2} \times \frac{n}{2}$ size 로 downsampling 하는 변환을 고려해 보자. MNIST, CIFAR-10 은 image size 가 $4 \times 4$ 가 될 때 까지, Celeb-A 는 image size 가 $2 \times 2$ 가 될 때까지 반복한다. Degraded 된 image 는 nearest-neighbor interpolation (최근접 보간법)을 통해 원본 image size 로 변환된다. Sampling 결과는 Figure 5. 와 Table 3. 에 나타나 있다.

4.4. Snowification

ImageNet-C 데이터셋에서 제안된 snowification 변환 을 적용해 보자. 일반적이지 않은 degradation 연산에 대해서도, generalized diffusion 이 성공적으로 이미지를 생성해 냄을 보인다. 매 step 마다 증가하는 snow 를 가함으로써 degradation 을 진행한다. Sampling (desnowification) 결과는 Figure 6. 와 Table 4. 에 나타나 있다.

5. Cold Generation

Diffusion model 은 데이터의 분포를 학습하고 높은 품질의 sample 을 생성해 낼 수 있다.

5.1. Generation using deterministic noise degradation

Noise 를 이용한 image generation 을 먼저 논의해 보자. 생성에 앞서, noise 의 종류가 미리 고정되어 있는 경우인 deterministic sampling 과정을 생각하자. 먼저, data point 와 고정된 noise $z \in \mathrm{N}(0, 1)$ 에 대한 deterministic interpolation 을 다음과 같이 정의하자.

D(x, t) = \sqrt{\alpha_t}x + \sqrt{1-\alpha_t} z

이 때 $\{ \alpha_t \}$ 는 증가수열이다.

Fixed noise method

고정된 noise $z$ 에 대해 degradation operator $D(x, s)$ 를 이용해 Algorithm 2. 를 적용할 수 있다.

Estimated noise method

반면, step $t$ 에서의 reconstruction 에서 사용될 수 있는 noise vector $\hat{z}$ 를

\hat{z}(x_t, t) = \frac{x_t - \sqrt{\alpha_t} R(x_t, t)}{\sqrt{1-\alpha_t}}

를 이용해 구하고 Algorithm 2. 에 적용시킬 수도 있다. 식을 조금 더 자세히 풀어보자. $R(x_t, t) = \hat{x_0}$ 이므로

\hat{z}(x_t, t) = \frac{x_t - \sqrt{\alpha_t} \hat{x_0}}{\sqrt{1-\alpha_t}}

가 성립하고,

D(\hat{x_0}, t) = \sqrt{\alpha_t} \hat{x_0} + \sqrt{1-\alpha_t} \hat{z}

D(\hat{x_0}, t-1) = \sqrt{\alpha_{t-1}} \hat{x_0} + \sqrt{1-\alpha_{t-1}} \hat{z}

이를 Algorithm 2. 에 대입하면 (sampling),

x_{t-1} = \sqrt{\alpha_{t-1}} \hat{x_0} + \sqrt{1-\alpha_{t-1}} \hat{z}

과 같다.

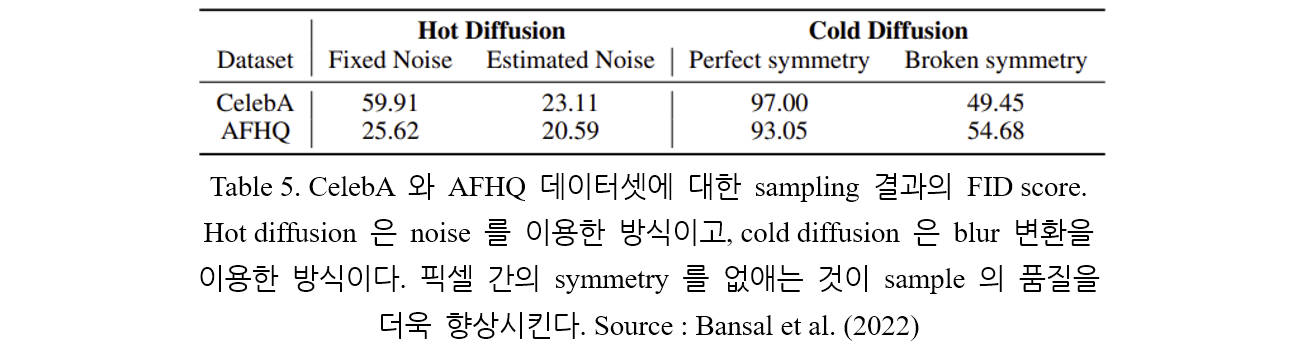
Table 5. 는 fixed noise method 와 estimated noise method 를 이용해 CelebA 와 AFHQ 데이터셋에 대해 sampling 을 진행한 결과 (Hot diffusion)를 정량적으로 나타낸다.

5.2. Image generation using blur

Noise 를 사용하는 diffusion 의 장점은 마지막 forward step 에서 degraded 된 image 는 isotropic gaussian distribution 을 따른다는 점이다. 따라서 isotropic gaussian distribution 으로부터 시작해 backward diffusion 을 적용하면 class-unconditional generation 을 수행할 수 있다.

Degradation operation 으로 blurring 을 사용할 경우, 완전히 degraded 된 이미지들은 sampling 을 진행할 수 있는 closed-form 으로 표현되지 않는다. 그러나 이 역시 간단한 method 를 통해 모델링 될 수 있는 분포에 해당한다. 매우 큰 값의 $T$ 에 대해, 모든 이미지 $x_0$ 가 모든 픽셀 값이 같은 색을 나타내는 $x_T$ 로 변형된다고 가정하자. 이 때 $x_T$ 의 일정한 픽셀 값 (RGB)은 원본 이미지 $x_0$ 의 RGB 채널의 평균값으로, 3차원 벡터를 통해 표현된다. 이러한 3차원 분포는 Gaussian mixture model (GMM) 을 통해 표현될 수 있다. GMM 을 이용한 sampling 으로부터, blur 정도가 약해진 random pixel 값을 가지는 이미지를 생성해 cold diffusion 을 적용시킬 수 있다.

논문에서는, $27 \times 27$ 크기의 gaussian kernel 을 통해 총 300번 이미지를 blur 시킨다. Kernel 의 표준편차는 1부터 시작해 0.01 의 비율로 증가한다. Sampling 은 다음과 같이 일어난다. 하나의 성분인 채널 별 평균의 분포를 따르게끔 GMM 을 생성하고, 이미지의 각 채널 별 평균을 GMM 으로부터 sampling (3차원 벡터) 한다. 이후 3차원 벡터를 $3 \times 128 \times 128$ 로 expand 하고 Algorithm 2. 를 적용한다. 이러한 방식으로 sampling 된 결과는 하나의 GMM 으로부터 채널 별 평균을 얻어져서 만들어진 결과이므로 pixel 간 perfectly correlated 되어 있으므로 Perfect symmetry 라고 표기한다. Symmetry 를 제거하기 위해 샘플링 된 $x_T$ 의 각 픽셀마다 작은 gaussian noise ( $\sigma = 0.002$ )를 추가한다 (Broken symmetry). 두 방식에 대한 비교는 Table 5. 에 나타나 있다. Figure 7. 은 blur 를 이용한 cold diffusion 의 sampling 결과를 나타낸다.

5.3. Generation using other transformations

이제, 다양한 transformation 이 image generating 에 적용될 수 있음을 보이자.

Gaussian Mask

Mask transformation 을 적용하기 위해, 최종적으로 degraded 된 이미지가 원본 이미지에 대한 정보를 전혀 포함하지 않을 정도로 masking routine 을 수정하자. 물론 모든 원본 이미지를 검정 이미지로 변환할 수 도 있지만 이는 다양한 이미지 생성에 어려움을 가져온다. 대신에 모든 픽셀을 랜덤한 단색으로 변형시키는 변환을 생각한다. 이는 원본 이미지에서 정보를 지울뿐더러, 서로 다른 색상의 이미지에 Algorithm 2. 를 적용시켜 다양한 sample 을 생성할 수 있게 해 준다. Gaussian mask 를

G_t = \Pi^t_{i=1} z_{\beta_i}

에 대해, $x_t$ 를 다음과 같이 생성한다. 4.2. 절의 방법과 유사하지만 약간의 차이가 있다. 랜덤 색상의 이미지를 $c$ 라고 하면,

x_t = G_t * x_0 + (1-G_t) * c

cf ) In 4.2. Inpainting : $x_t = D(x_0, t) =x_0 \cdot \Pi^t_{i=1}z_{\beta_i}$

Super-resolution

Super-resolution 의 경우 이미지를 $2 \times 2$ 또는 $4 \times 4$ 로 downsampling 하였다. 이렇게 degraded 된 이미지들은 1차원 벡터로 표현될 수 있고, 하나의 gaussian distribution 을 통해 모델링 될 수 있다. 이후 blurring 과 같은 방식으로 sampling 을 하여서 학습된 super-resolution 모델을 이용하면 이미지를 얻을 수 있다.

Animorphosis

어떠한 형태의 변환이 적용될 수 있다는 점을 보이기 위해, animorphosis 라는 새로운 변환을 이용해보자. CelebA 데이터셋에서 인간의 얼굴을 AFHQ 의 동물 얼굴로 변환하는 것이다. 논문에서는 CelebA 와 AFHQ 데이터셋을 이용하였지만 어떠한 두 분포에 대해서도 근본적으로는 적용 가능하다. 과정을 수식으로 나타내면 아래와 같다. CelebA 의 이미지 $x$ 와 AFHQ 의 이미지 $z$ 에 대해,

x_t = \sqrt{\alpha_t} x+ \sqrt{1-\alpha_t} z

이는 noise 를 가하는 과정과 같지만, $z$ 가 (Gaussian) noise 가 아닌 AFHQ 이미지라는 차이점이 있다. Algorithm 2. 를 이용해 sampling 을 진행한다.

Results

Inpainting (Gaussian mask), Super-resolution, Animorphosis 를 적용한 각각에 대한 FID score 는 90.14, 92.91, 48.51 이다. 실제 sampling 결과는 Figure 1. 과 Figure 8. 에 나타나 있다.

6. Conclusion

현존하는 diffusion model 은 forward process 와 reverse process 두 과정 모두 gaussian noise 를 사용한다. 논문에서는 noise 를 사용하지 않고, 임의의 변환을 이용해서도 diffusion process 를 수행할 수 있음을 보였다. 이를 통해 diffusion model 을 일반화 (generalize) 하며, blurring, inpainting, downsampling 과 같은 변환으로 deterministic degradation 을 적용해 이미지를 생성한다. 이를 통해 diffusion model 의 활용 범위와 적용 방식을 확장시킨다.

Reference

[1] Arpit Bansal, Eitan Borgnia, Hong-Min Chu, Jie S. Li, Hamid Kazemi, Furong Huang, Micah Goldblum, Jonas Geiping, Tom Goldstein. Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise, CVPR, arXiv:2208.09392, 2022.

Hyunsoo Lee

이전 포스트

Denoising Diffusion Probabilistic Models

다음 포스트