Generative Adversarial Networks

대표적인 Deep generative model 중 하나인 GAN (Generative Adversarial Network) 를 처음 소개한 논문을 리뷰해 보았다.

Original Paper : Goodfellow, I. et al., 2014.

Abstract

Adversarial process (경쟁 과정)을 통해 generative model 을 추정 (estimate)하는 새로운 프레임워크를 제안하였다.

• 2개의 모델을 동시에 학습

  • G (Generator) : 데이터 분포를 학습, D가 실수할 확률을 최대화
    
  • D (Discriminator) : 샘플된 데이터가 ‘G에 의해 생성된 데이터가 아니라 학습 데이터 (=실제 데이터)일 확률’ 을 추정
  • Minimax two-player game 을 통해 2개의 모델을 동시에 학습

• 임의의 함수 집합에 속한 두 함수 G, D 에 대해 아래 조건을 만족하는 유일한 해가 존재

  • G : 훈련 데이터 분포 학습 (논문에서는 recover 이라는 워딩을 사용하였지만, 이는 실제 학습 데이터의 분포를 완벽히 catch 한다고 해석)
  • D : 함숫값이 0.5인 상수함수

• G, D 를 다층 퍼셉트론으로 정의할 시 역전파를 통해 모델 학습 가능

  • 마르코프 체인은 필요하지 않음

Introduction

DL model 의 목표 : AI 에 활용될 수 있는 여러 종류의 데이터 (이미지, 음원 파형, 자연어 등)에 대한 확률 분포를 표현할 수 있는 계층적인 모델을 개발하는 것

• 이러한 목표에 가장 가까웠던 시도들 중에는 ‘discriminative model’ 이 있음.

• 위와 같은 성공적인 시도들은 역전파 및 Dropout 에 기반한 시도들이 많음

  • Piecewise linear unit (Dropout의 원리; 조각적인 선형 레이어) with well-behaved gradient

• 반면, Deep generative model 은 이러한 목표에 대해 많은 영향력을 주지 못하였음.

  • (1) MLE 와 같은 전략에서 발생하는 확률적 계산을 근사하는 데 어려움을 가졌기 때문
  • (2) piecewise linear unit 의 장점을 잘 반영하지 못함

이 논문에서는, (1) 및 (2)와 같은 단점을 극복할 수 있는 새로운 generative model 을 제안.

• 논문에서 제안된 Adversarial net : generative model 과 discriminative mode 은 경쟁적 구도를 가짐

  • Generative model : [counterfeiters] 거짓 정보를 생산하고 이가 감지되지 않게끔 하는 역할
  • Discriminative model : [police] 거짓 정보를 감지 및 판별
  • 두 모델의 경쟁은 각각의 성능을 발전시키며, 결과적으로 거짓 정보가 실제 정보와 구분될 수 없을 때 까지 계속됨

해당 프레임워크 학습을 위해서는 다양한 종류의 최적화 알고리즘이 사용될 수 있음

• 이 논문에서는, G가 다층 퍼셉트론으로 구성되어 있고 각 층에서 random noise 를 추가해 이미지를 생성하는 경우 그리고 D가 다층 퍼셉트론으로 구성되어 있는 경우에 대해서 다룸

• 이를 adversarial net 이라고 지칭

  • 두 개의 모델을, 역전파 / dropout / 순전파를 통한 G에 대한 sampling 만을 통해 학습
  • 마르코프 체인과 Appoximate Inference 와 같은 기법은 사용하지 않음

Adversarial nets

Adversrial modeling framework → 두 개의 모델이 모두 다층 퍼셉트론으로 구성되어 있을 때 가장 직관적, 이 연구에서도 이를 사용

Model 정의 및 Notation
1) Global notation

• 학습 데이터 = $G$로부터 생성되지 않은 true data = training examples

2) Generative model : $G$

• $G$를 통과한 데이터 ($x$) 의 분포 : $p_g$
• Input noise variables (to G) : $p_{\bold{z}} (\bold{z})$
• 다층 퍼셉트론의 parameter : $\theta_g$
• 치역 (mapping space) : $G(\bold{z}; \ \theta_g)$
  → 거짓 이미지가 학습 데이터에 가까워지도록 학습 → minimizing $\log(1-D(G(\bold{z}))$

3) Discriminative model : $D$

• 다층 퍼셉트론의 parameter : $\theta_d$
• $D(\bold{x}, \ \theta_d) \in \R$ → $\bold{x}$가 $p_g$ 가 아닌, 학습데이터에 속할 확률을 나타냄
  → 1) Training example 과 2) $G$로부터 sample 된 data에 대해 올바른 label 을 부여할 확률을 최대화하는 방향으로 학습
  

Minimax game

💡 Discriminator and Generator are playing two-player minimax game!

목적 함수를 $V(G, D)$ 라고 하면 minimax game 을 나타낸 수식은

첫 번재 항은 D 에 대한 최적화를, 두 번째 항은 G 에 대한 최적화를 나타낸다.

Training Algorithm

Figure 1. Algorithm for training GAN (Figure source : Goodfellow, I. et al., 2014.)

학습 과정을 나타내는 loop 에서 D를 완전히 최적화 하는 것은 매우 많은 연산을 필요로 하며, 유한한 데이터셋에 대해 이를 수행할 경우 overfitting 이 발생할 수도 있다.

• 따라서, G 를 최적화 하는 step 마다 D 를 최적화 하는 step 을 $k$번 수행
• G는 천천히 학습되며, D가 optimal solution 근처에 머무르며 수렴하는 방향으로 학습이 진행됨
• SML/PCD 에서 사용된 방식과 유사

1) Training D

• maximize 를 위해 Gradient ascent 기법 사용
  
  

2) Training G

• 실제 학습 시에는 $\log{(1-D(G(\bold{z})))}$ 를 minimize 하는 것 대신, $\log(D(G(\bold{z}))$ 를 maximize 하게끔 G 를 학습시킴.

  • 두 식 모두 $\bold{z}$에 대한 gradient 는 같으므로, G, D 를 모두 같은 point 로 수렴하게 함
  • 학습 초기에 $\log{(1-D(G(\bold{z})))}$가 saturate 되는 문제를 방지하기 위해 사용된 기법

• 학습 초기에는 G 의 성능이 좋지 않으므로, D 가 쉽게 학습 데이터와 거짓 이미지를 구분할 수 있고, 결과적으로 $\log{(1-D(G(\bold{z})))} \rightarrow \infin$ 가 발생 (saturate).

Training examples

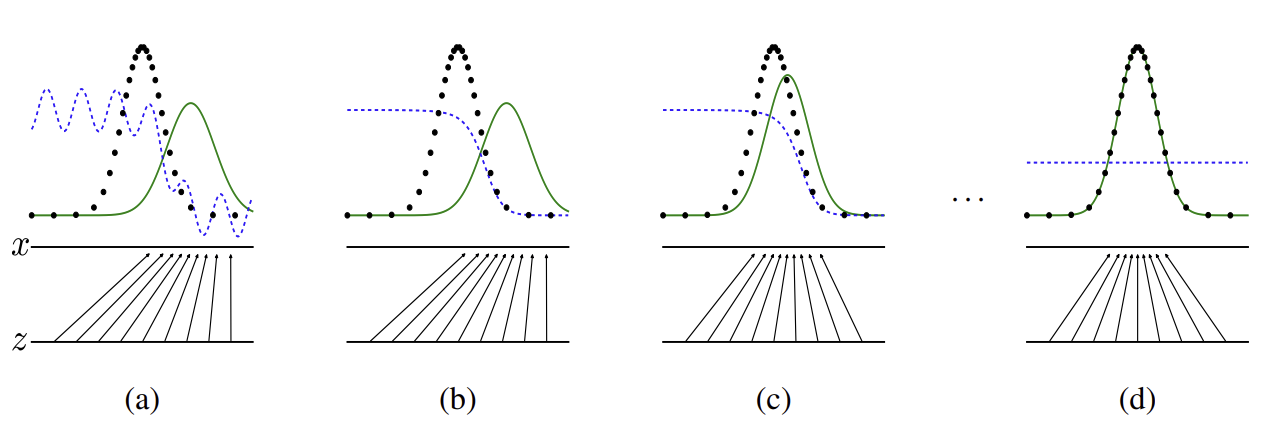Figure 2. Distribution of variables. (Figure source : Goodfellow, I. et al., 2014.)

1) Notation

• blue dashed line : distribution of discriminator
• black dotted line : distribution of data generating (real) → $p_{data}$
• green solid line : distribution of generator’s generative distribution (fake) → $p_g$
• lower horizontal line : domain of $\bold{z}$ (sampled) → in this case, uniform distribution
• upper horiziontal line : domain of $\bold{x}$
• upward arrows : mapping $\bold{x} = G(\bold{z})$

2) Explanation

• a) $p_{data}$와 $p_g$는 유사하지만 완벽히 일치하지 않는다. Discriminator 의 경우, 비교적 정확한 분류를 해 낸다 (예측한 확률이 1에 가까운 부분과 0에 가까운 부분이 드러남)

• b) D 를 optimize 하는 loop 를 통과한 후의 상태. a) 에 비해 discriminator 의 성능이 높아짐을 확인할 수 있으며, training data와 G에 의해 sample 된 데이터를 구분한다.

• c) G 를 optimize 하는 loop 를 통과한 후의 상태. $G(\bold{z})$가 실제 학습 데이터에 가까운 부분을 나타내도록 학습되었다.

• d) a) ~ c) 를 여러 번 반복해 학습된 후의 상태. 충분히 학습되었다면 $p_g = p_{data}$ 에 도달하고 더 이상 성능이 향상되지 않는다. D 는 학습 데이터와 G 로부터 sample 된 데이터를 구분할 수 없는 상태에 도달한다. 즉, $D(G(\bold{x})) = 1/2$ 인 상태이다.

Theoretical Results

G가 정의하는 확률분포 $p_g$ : $\bold z \sim p_z$ 를 이용해 샘플링된 변수들 ($G(\bold{z})$)의 분포와 동일

• 따라서, 위에 제시된 알고리즘이 충분한 자원/시간이 있다면 $p_{data}$에 대한 좋은 estimator 가 될 수 있음
• 이 절에서는 위 내용을 증명하고자 함

---

Global Optimality of $p_g = p_{data}$

💡 Minmax game has a global optimum.

Prop 1 고정된 G 에 대해, D의 optimal solution 이 존재하며 이는 아래 식과 같다.

Proof 고정된 G 에 대한 optimization problem (for D) 는 다음 식과 같이 나타난다.

이 때 $V(D)$를 다시 계산해보면,

적분변수를 $\bold{x}$로 통일하자. $\overline{G}(\bold{z}) = \bold{x}$ 로 두면, $\overline{G}(\bold{z})$ 의 분포는 $p_g$ 를 따르게 된다. 따라서,

가 성립한다. 이 때, 간단한 로그함수 예제를 살펴보면 $^\forall (a, \ b) \in \R^2 \ \backslash \ (0, 0)$ 에 대해 $f(x) = a \log x+ b \log (1-x)$ 는 $x = \frac{a}{a+b}$ 에서 최댓값을 가진다. 우리는 $V(D)$ 를 maximize 해야 하고, 피적분함수는

일 때 최댓값을 가진다.

Prop 1을 이용해, minimax problem 을 아래와 같이 나타낼 수 있다. Virtual training criterion $(C(G))$ 을 다음과 같이 정의하자. Fixed G 에 대한 optimization problem 에 $D_G ^* (\bold{x})$ 의 식을 대입하면,

Thm 1 $C(G)$가 최소가 되기 위한 필요충분조건은 $p_g = p_{data}$ 이며, 이 때의 최솟값은 $-\log4$ 이다.

Proof 만약 $p_g = p_{data}$ 가 성립한다면, 이 때 $C(G) = -\log4$ 이다. 따라서 $C(G)$ 에서 $\log 4$ 를 빼 보자. 이 때 KL-divergence 의 정의를 기억하자. 연속확률변수 $P, Q$ 에 대해서 각각의 확률밀도함수를 $p(x), q(x)$ 라고 하면

이다. 따라서,

가 성립한다. KL-divergence 내부 분모 2가 $-\log 4$로부터 나온 항임을 기억하자. 이제 두 개의 KL-divergence 항을 Jensen-Shannon divergene 를 이용해 정리하자.

정의를 이용하면,

여기서 Jensen-Shannon divergene 의 성질 중, non-negative 한 성질을 이용하자. 결과적으로

가 성립하고 등호는 $p_{data} = p_g$ 일 때 성립한다. 따라서 $C(G)$의 최솟값은 $-\log4$ 이며, 이를 만족시키는 유일한 해는 $p_g = p_{data}$ 이다.

따라서, 논문에서 제시한 generative model 은 original data의 분포를 완전히 copy 할 수 있다.

---

Convergence of Algorithm 1

Prop 2 만약 1) G, D의 모델 크기가 충분하고, 2) Algorithm 1의 매 loop 마다 D가 해당 step 의 G에 대해 $D^*$에 도달할 수 있고, $p_g$가 $\mathbb{E}_{\bold{x} \sim p_{data} (\bold{x})} [\log D^*_G(\bold{x})] + \mathbb{E}_{\bold{x} \sim p_{g}(\bold{x})} [\log(1- D^*_G(\bold{z}))]$ 를 최대화 시키는 방향으로 학습된다면, $p_g \rightarrow p_{data}$.

Proof 앞서 $V(G, D)$에서 치환을 통해 $G$에 대한 항을 $p_g$를 이용해 표현하였으므로, $V(G, D)=U(p_g, D)$ 로 쓸 수 있다. 이 때, 다음과 같은 사실을 이용하자.

만약 $f(x) = \sup_{\alpha \in A}f_{\alpha}(x)$ 이고 모든 $\alpha$에 대해 $f_{\alpha}(x)$가 convex 하다면, $\beta = \arg \sup _{\alpha \in A}f_{\alpha}(x)$ 에 대해 $\partial f_{\beta}(x) \in \partial f$ 가 성립한다.

Prop 2 의 경우, $U(p_g, D)$가 $p_g$에 대해 convex 하고, 주어진 G에 대한 $D^*$에서 $p_g$에 대한 gradient 를 구하는 상황이다. $\sup_D U(p_g, D)$ 역시 $p_g$에 대해 convex 하며, Thm 1. 에서 증명한 바와 같이 유일한 최솟값을 가지므로, $p_g$에 대해 충분히 작은 양의 변화를 주면 $p_g$는 $p_{data}$ 로 수렴한다.

In practice

G, D 2개의 layer는 다층 퍼셉트론이며, 각각은 파라미터 $\theta_g, \ \theta_d$ 로 표현된다. 따라서 실제로는 $p_g$ 를 이상적인 형태 ($p_{data}$)로 최적화 시키기 보다는 $\theta_g$에 대한 최적화를 진행한다. 따라서 모든 $p_g$를 나타내지는 못하며, parameter space 의 관점에서 볼 때는 주어진 최적화 문제를 해결하는 여러 개의 임계점 (critical point) 가 존재한다. 그러나, 위에 나타난 증명의 경우 모델이 infinite capacity 를 가진다고 가정한 상태 (parameter 와 같은 제한을 가지지 않는 상태)에서 성립한다. 따라서 실제 학습에서 사용한 모델이 위에서 제시한 이론적 배경을 완벽하게 만족하는 것은 아니다. 다만 다층 퍼셉트론을 이용한 경우에도 좋은 성능이 나타난 것으로부터, 다층 퍼셉트론은 이론을 완벽하게 만족하지 못하는 상태에서 사용하기에 합리적인 모델임을 알 수 있다.

Experiments

기본 모델 세팅

• 사용한 데이터셋 : MNIST, TFD, CIFAR-10
• Activation function
  • G : ReLU + Sigmoid
  • D : maxout
• Dropout on D
• G의 첫 번째 layer에 입력으로 noise 를 사용, 이후 layer 에서는 noise 를 따로 주지 않음

Results

Gaussian Parzen window 를 이용해 test set 과 G 를 통해 생성된 데이터 사이 ($p_g$의 분포를 나타냄) 의 log-likelihood 측정.

• Gaussian 에서 parameter $\sigma$의 경우 validation data를 이용한 Cross-validation 을 통해 결정됨

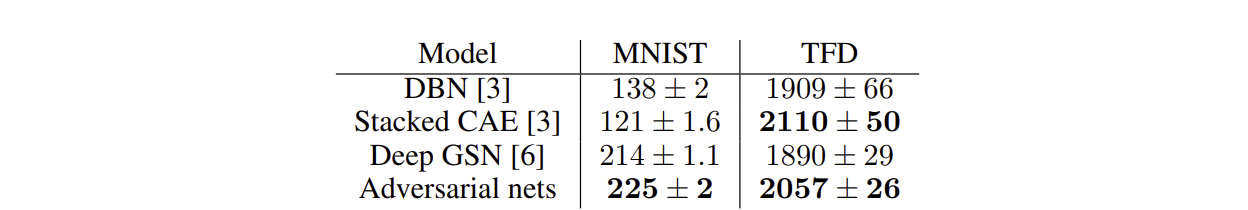Figure 3. Parzen window 를 이용한 log-likelihood
측정 결과. 평균과 분산을 함께 나타내었다.
(Figure source : Goodfellow, I. et al., 2014.)

• 이러한 방식으로 log-likelihood 를 측정하는 것은 그 측정 결과의 분산도 크고 고차원 공간에서 좋은 결과를 나타내지 못하지만, (당시의) 지식 수준에서 사용할 수 있는 방법 중 가장 좋은 방법이었다.
• Sampling 은 가능하지만, likelihood 를 정확히 측정할 수 없는 점은 후속 연구를 통해 개선될 여지가 있다.
• 아래 그림은 G network 를 학습시킨 후 sampling 한 결과를 나타낸다.

Figure 4. G를 학습시킨 후 sampling 한 결과. 각각 a) MNIST b) TFD c) CIFAR-10 with fully-connected model d) CIFAR-10 with deconvolutional generator 를 이용해 sampling 한 결과이다.(Figure source : Goodfellow, I. et al., 2014.)
Figure 5. Fully-connected generator model 에 대해,
z-space 의 좌표들 간 보간을 통해 얻은 결과를 나타낸다.
(Figure source : Goodfellow, I. et al., 2014.)

Advantages and disadvantages

이전 모델들과의 비교를 통해 장/단점을 분석해 보면 아래와 같다.

Disadvantages

1. $p_g (\bold{x})$를 직접적으로 표현할 수 없다.
2. G와 D가 적절하게 반복되며 업데이트 되어야 한다. (Synchronizing 이 되어야 한다)
   • D를 업데이트하지 않고 G를 계속해서 업데이트 하는 것은 방지해야 한다.

Advantages

[Computational advantage]

1. 마르코프 체인이 전혀 필요하지 않다. Gradient 를 계산하기 위해서는 역전파 만으로도 충분하다.
2. 학습 과정에서 inference 가 필요하지 않다.
3. 여러 가지 미분가능한 함수들을 통해 모델을 구축할 수 있다.

[Statistical advantage]

1. G는 학습 데이터로부터 직접적으로 업데이트 되지 않고, D에서 계산된 gradient 만을 이용해 업데이트 된다.
   • 즉, 입력되는 학습 데이터는 G network 에는 입력 (복사)될 필요가 없다.
     
     
2. Sharp / degenerate distribution (퇴화 분포) 을 표현할 수 있다.
   • 마르코프 체인에 기반한 network 의 경우 이러한 분포들을 명확히 나타내지 못한다.

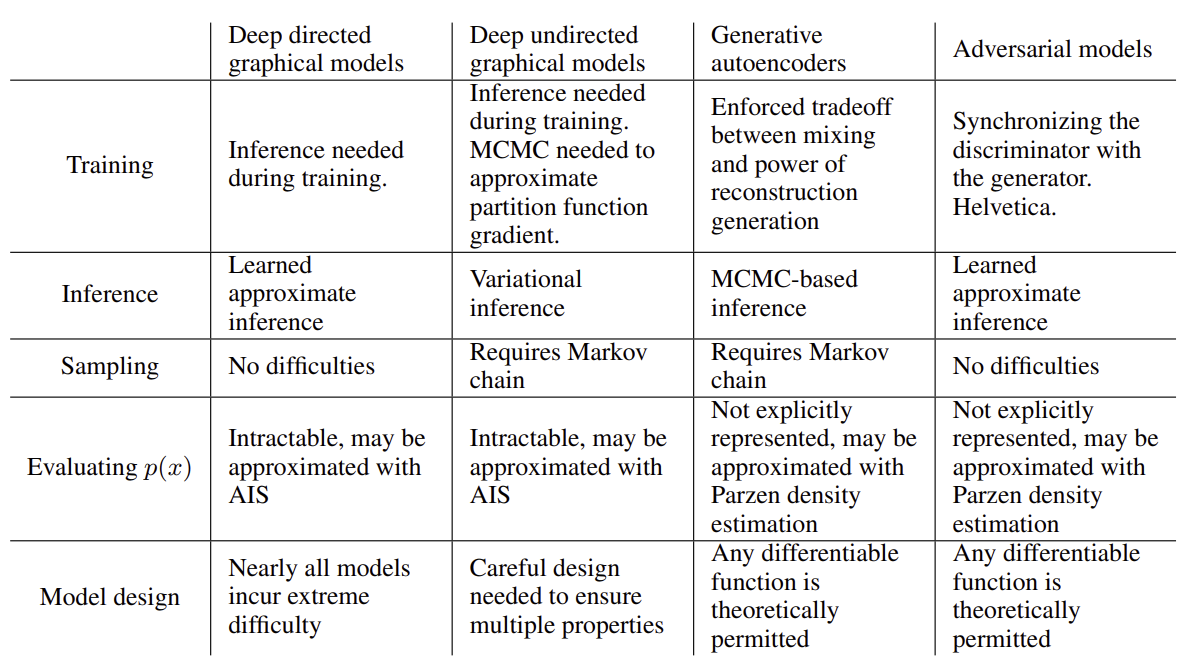Figure 6. 여러 가지 deep generative model 의 특징 비교.
(Figure source : Goodfellow, I. et al., 2014.)

Conclusions and future work

이 논문에서 제시한 framework 는 다양한 확장 가능성을 가진다. 크게 5가지의 가능성을 제시한다.

1. Conditional generative model

   • G, D network 에 모두 $\bold{c}$를 입력해 준다면, $p(\bold{x} | \bold{c})$ 를 얻을 수 있다.

2. Learned approximate inference

   • $\bold{x}$가 주어졌을 때 $\bold{z}$를 예측하는 auxiliary network (보조 신경망)을 학습시켜 수행할 수 있다.

3. $p(\bold{x}_S | \bold{x}_{\not S})$ 을 근사적으로 모델링할 수 있다.

   • $S$ : $\bold{x}$의 인덱스들로 이루어진 부분집합
   • parameter 를 공유하는 conditional model 집합을 학습시킴으로써 얻을 수 있다.

4. Semi-supervised learning

   • 일부 데이터에 대해 label 이 존재한다면, D에서 추출된 feature 또는 inference net을 통해 classifier 의 성능을 향상시킬 수 있다.

5. Efficiency improvements

   • G, D 를 학습시키기 위한 더 나은 방법을 각각 나누어서 제시하거나, 학습 과정에서 $\bold{z}$를 samling 하기 위한 분포를 바꾸어 학습을 가속화시킬 수 있다.

이 논문은 적대 신경망이 성공적이라는 것을 입증하였으며, 이러한 연구 방향이 유용할 수 있다는 것을 보여주었다.