서포트 벡터 머신(SVM)

SVM

• 특성의 가중치 벡터 : $w$ / 편향 : b

선형 SVM 분류 모델 이론

결정 함수와 예측

• 선형 SVM 분류 모델은 $w^Tx + b = w_1x_1 + ••• + w_nx_n + b$를 계산하여 새로운 샘플 $x$의 클래스를 예측한다.
• 예측 결과 : $\hat{y} = \begin{cases} 0,\,\,　w^Tx + b<0\\ 1,\,\,　w^Tx + b\geq0 \end{cases}$

목적 함수

• 결정 함수의 기울기 = $\lVert w \rVert$
• $margin \propto \frac{1}{\lVert w \rVert}$
• 하드 마진 분류기
  $minimize\frac{1}{2}w^Tw$
  조건: $i=1,2,•••,m$ 일 때 $t^{(i)}(w^Tx^{(i)} + b)\geq1$
  $t^{(i)}$는 결괏값
• 소프트 마진 분류기
  $minimize\frac{1}{2}w^Tw + C\displaystyle\sum_{i=1}^{m}{ξ^{(i)}}$
  조건: $i=1,2,•••,m$ 일 때 $t^{(i)}(w^Tx^{(i)} + b)\geq1-ξ^{(i)}$이고 $ξ^{(i)}\geq0$
  $ξ^{(i)}$는 슬랙 변수 : 각 샘플이 얼마나 마진을 위반하는지를 나타내는 변수

커널 SVM

(아래는 2차원의 예시)
$\phi(x) = \phi(\begin{pmatrix}x_1\\x_2\\ \end{pmatrix}) = \begin{pmatrix}x_1^2\\\sqrt{2}x_1x_2\\x_2^2\\ \end{pmatrix}$
에서
$\phi(a)^T\phi(b) = \begin{pmatrix}a_1^2\\\sqrt{2}a_1a_2\\a_2^2\\ \end{pmatrix}^T\begin{pmatrix}b_1^2\\\sqrt{2}b_1b_2\\b_2^2\\ \end{pmatrix} = a_1^2b_1^2 + 2a_1b_1a_2b_2 + a_2^2b_2^2 = (a_1b_1 + a_2b_2)^2 = (\begin{pmatrix}a_1\\a_2\\ \end{pmatrix}^T\begin{pmatrix}b_1\\b_2\\ \end{pmatrix})^2 = (a^Tb)^2$ 이므로
$\phi(a)^T\phi(b) = (a^Tb)^2$ 즉, 변환된 벡터의 점곱이 원래 벡터의 점곱과 같다.
여기서 함수 $K(a,b) = (a^Tb)^2$을 2차 다항식 커널이라고 부른다.
다항식 커널을 이용하면 변환 $\phi$를 계산하지 않고 $a$와 $b$만으로 $\phi(a)^T\phi(b)$를 계산할 수 있다. - 머서의 정리

일반적인 커널
선형: $K(a,b) = (a^Tb)^2$
다항식: $K(a,b) = (\gamma a^Tb + r)^d$
가우시안 RBF: $K(a,b) = exp(-\gamma \lVert a-b \rVert^2)$
시그모이드: $K(a,b) = tanh(\gamma a^Tb + r)$

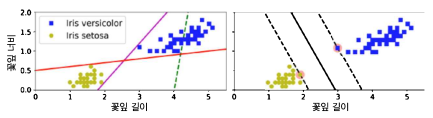
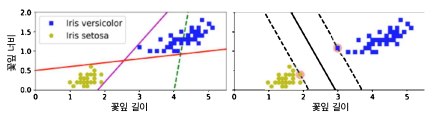
선형 SVM 분류

• 두 개의 클래스 중 새로운 데이터가 어느 클래스에 해당하는지 판단하는 비확률적 이진 선형 분류 모델
• 위 그림에서 오른쪽 그래프의 실선은 두 개의 클래스를 나누며, 제일 가까운 훈련 샘플로부터 가능한 멀리 떨어져 있는 SVM 분류기의 결정 경계이다.
• 같은 그래프의 결정경계 마진(라지 마진 분류)은 두 점선 사이의 공간(도로에 비유할 수 있다.)인데, 이 공간의 경계에 위치한 샘플에 의해서 공간이 결정된다. 이러한 샘플들을 서포트 벡터(Support Vector)라고 한다.
• 복잡한 분류 문제에 잘 맞고, 중간 크기 이하의 데이터셋에 적합하다.
• 클래스에 대한 확률을 제공하지 않는다.

SVM은 특성의 스케일에 민감하므로 StandardScaler를 사용하여 표준화를 적용하면 결정 경계가 훨씬 좋아진다.

하드 마진 분류(Hard Margin Classification)

• 모든 샘플이 도로 바깥쪽에 올바르게 분류되어 있는 마진 분류
• 문제점
  • 데이터가 선형적으로 구분될 수 있어야 한다.
  • 이상치에 민감하다.(마진 오류)

소프트 마진 분류(Soft Margin Classification)

• 도로의 폭을 가능한 넓게 유지하는 것과 마진 오류(샘플이 도로 중간이나 반대쪽에 있는 경우) 사이에서 조절하는 마진 분류
• 사이킷런의 SVM 모델에서 하이퍼 파라미터 C(도로 폭에 반비례한 값)를 조절하여 도로 폭을 조절할 수 있다.

비선형 SVM 분류

• 선형적으로 분류할 수 없는 데이터셋에 사용
• 데이터셋에 특성을 하나 더 추가하여 선형적으로 구분이 되도록 한다. (PolynomialFeatures를 활용할 수 있다.)

다항식 커널

• 다항식의 차수에 대한 딜레마
  • 차수가 낮으면 -> 매우 복잡한 데이터셋을 잘 표현하지 못한다.
  • 차수가 높으면 -> 특성이 너무 많아져 모델이 느려진다.
    * 해결방법 : 커널 트릭을 적용

커널 트릭(Kernel Trick)

• 선형 분류가 불가능한 데이터를 분류하기 위해 데이터의 차원을 증가시켜 하나의 초평면으로 분1류하도록 하는 것(이때 사용되는 함수를 커널 함수라고 한다.
• 실제로는 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있다.
• 아래로 갈수록 함수의 복잡성이 증가한다.
  선형함수(linear) : $x_i$
  다항함수(polynomial) : $(1+x_i x_j )^2$
  방사형 함수(radial basis) : $exp(-γ(x_i-x_j )^2)$
  시그모이드 함수(sigmoid) : $tanh⁡(κx_i x_j+C)$

유사도 특성

• 비선형 특성을 다루는 기법 중 하나
• 각 특성을 특정 랜드마크(landmark)와 얼마나 닮았는지 특정하는 유사도 함수(Similarity Function)로 계산한 특성을 추가하여 선형적으로 구분이 가능하도록 한다.

랜드마크 선택

• 배치, 미니배치, 확률적 경사 하강법처럼 무작위로 1개부터 전체까지를 랜드마크로 선택할 수 있는데, 랜드마크가 많을 수록 변환된 훈련 데이터셋이 선형적으로 구분될 확률이 높아지지만 랜드마크 개수와 같은 수의 특성이 생성된다는 단점이 있다.
• 따라서 적절하게 랜드마크 수를 설정해야 하는데 여기에도 커널 트릭을 적용할 수 있다.

SVM 회귀

• 제한된 마진 오류(도로 밖의 샘플) 안에서 도로 안에 가능한 많은 샘플이 들어가도록 학습한다.
  즉, 마진 오류를 error로 하여 error가 최소가 되도록 학습한다.