[DLS] Neural Networks and Deep Learning week 4

피망이·2023년 12월 8일

1st Course 1 Coursera week 4

[DLS] Deep Learning Specialization

목록 보기

4/6

Deep Neural Network

Deep L-layer Neural network

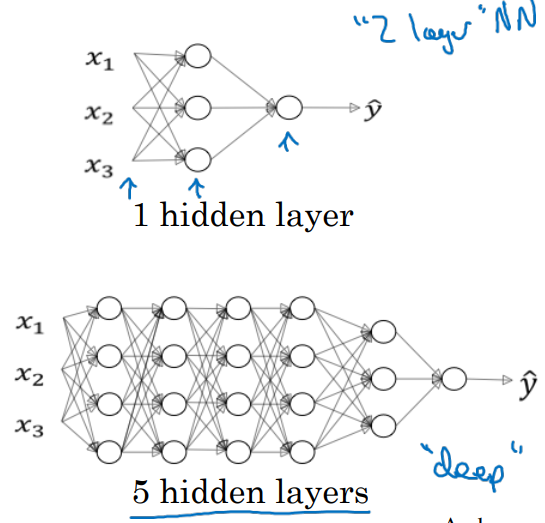
NN of deep layers is better than NN of shallow layer
- Hidden layer를 깊이 쌓을수록 성능이 좋아진다는 점이 실험적으로 증명되어 왔다.
Notation은 다음과 같다.
- 4 layer NN이라고 한다면,
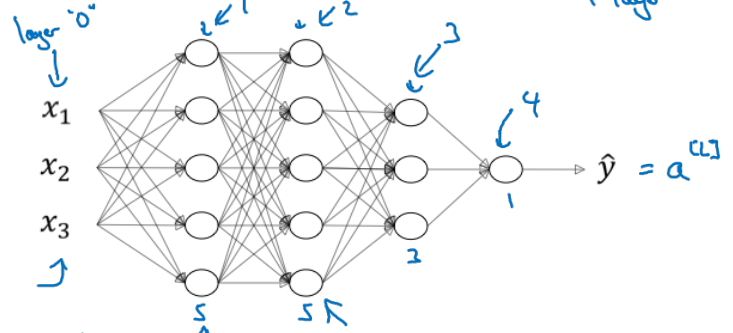
$L = 4$ (# of total layers)
$n^{[l]} =$ # units in layer $l$
$a^{[l]} =$ activations in layer $l$
$a^{[l]} = g^{[l]}$ , $W^{[l]} =$ weights for $z^{[l]}$
- $n^{[0]} = n_x = 3$ ← input x's
- $n^{[1]} = 5$ , $n^{[2]} = 5$ , $n^{[3]} = 3$ , $n^{[4]}=n^{[L]}=1$

Forward Propagation in a Deep Network

1st layer에 대한 forward propagation에 대해 살펴보자.
- $x$ 는 $a^{[0]}$ 와 같다는 점을 차용하여 propagation 식을 유도하면 다음과 같다.
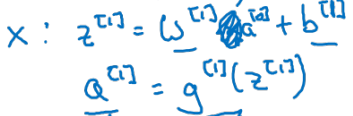
2nd layer에 대한 forward propagation은
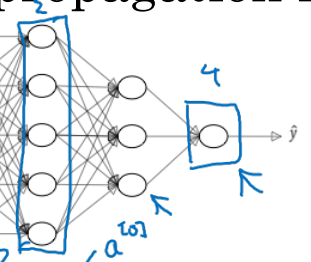
- 1st layer와 비슷한 형태로 layer number만 바뀌어 유도된다.
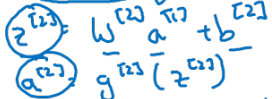
Training examples를 column 기준으로 stacking하여 matrix 형태로 나타내 보자.
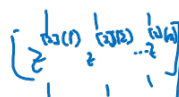
각 layer에서 연산되는 과정을 matrix 연산으로 Generalization 하면,
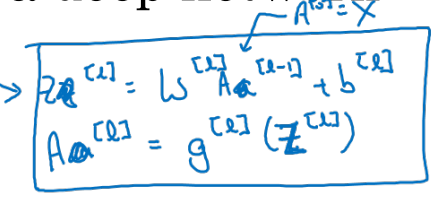
- 위와 같은 대문자(행렬식) 형태로 일반화 된다.
전체 layer 개수 $L$ 에 대한 for loop으로 연산 code를 작성하면 아래와 같다.
- for $l$ in range(1, L):
  $Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}$
  $$A^{[l]} = g^{[l]}(Z^{[l]})
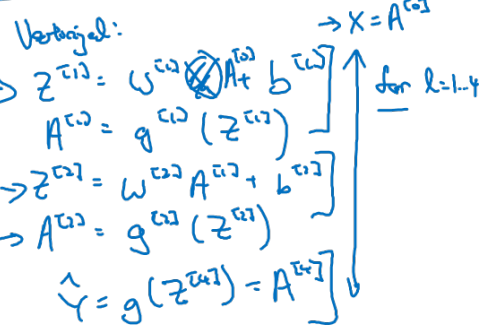
- layer를 연결하는 연산 과정은 for loop을 사용해야만 한다!

Getting your matrix dimensions right

Parameters $X^{[l]}$ 과 $b^{[l]}$ 의 dimension에 대해 생각해보자.
- 우선, 선형 변환으로 이루어진 $z^{[l]}$ 연산과 $a^{[l]}$ 연산은 shape이 같아야 한다.
  - Activation 함수에 집어넣을 것이기 때문!
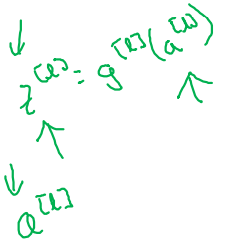
- 예를 들어 1st layer의 unit 개수가 3개이고, $x$ .shape = (2, 1)을 가진다고 할 때,
  - Activation으로 뽑아져 나오는 $a^{[1]}$ .shape & $z^{[1]}$ .shape = (3, 1)이어야 한다.
  - 행렬 곱 연산을 맞춰주기 위해 $W^{[1]}$ 과 $b^{[1]}$ 의 shape은 아래와 같아야 한다.
    - $z^{[1]} = W^{[1]} •x + b^{[1]} = W^{[1]} • a^{[0]} + b^{[1]}$
      (3, 1) = (3, 2) • (2, 1) + (3, 1)
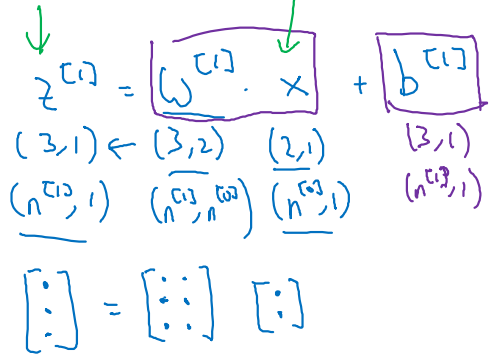
- 2nd layer의 unit 개수가 5개이고, 이전 $a^{[1]}$ .shape = (3, 1)이라면,
  - 최종 결과인 Activation $a^{[2]}$ .shape & $z^{[2]}$ .shape = (5, 1)이며,
  - 행렬 곱 연산을 맞춰주기 위한 $W^{[2]}$ 과 $b^{[2]}$ 의 shape은 아래와 같다.
    - $z^{[2]} = W^{[2]} • a^{[1]} + b^{[2]}$
      (5, 1) = (5, 3) • (3, 1) + (5, 1)
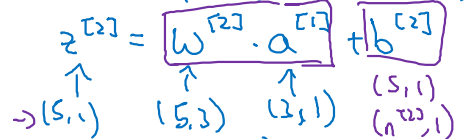
이를 통해 규칙성을 찾아보면 다음과 같이 정리된다. (derivative: 같은 shape)
- $W^{[l]}$ .shape = ( $n^{[l]}$ , $n^{[l-1]}$ )
- $b^{[l]}$ .shape = ( $n^{[l]}$ , 1)
- $dW^{[l]}$ .shape = ( $n^{[l]}$ , $n^{[l-1]}$ )
- $db^{[l]}$ .shape = ( $n^{[l]}$ , 1)
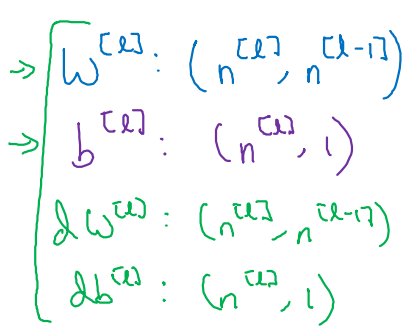
이제 m개의 training samples를 stacking하여 matrix 형태로 표현해보자.
- $z^{[l]} = W^{[l]} • X + b^{[l]} = W^{[l]} • A^{[l-1]} + b^{[1]}$
  ( $n^{[l]}$ , m) = ( $n^{[l]}$ , $n^{[l-1]}$ ) • ( $n^{[l-1]}$ , m) + ( $n^{[l]}$ , 1 ~> m)
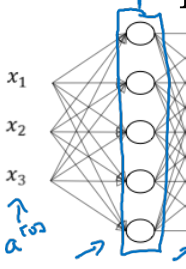
- 아래 그림은 1st layer에 관한 notation이다.
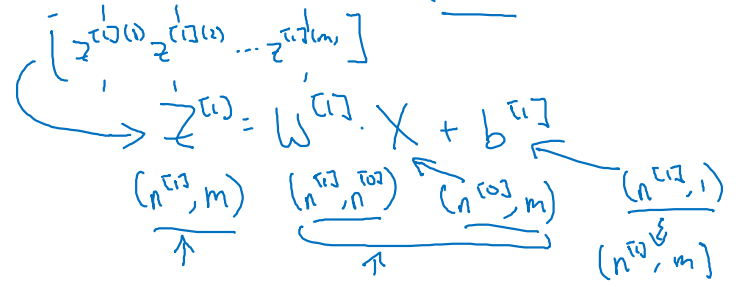
- Activatino $A^{[l]}$ 또한 $Z^{[l]}$ 의 shape과 같고, $dA^{[l]}$ 와 $dZ^{[l]}$ 또한 동일하다!

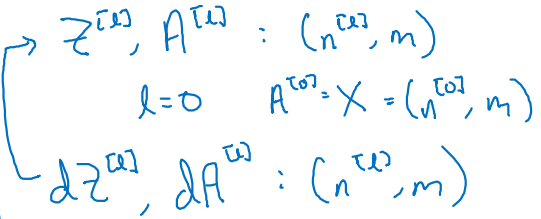
Why deep representations?

왜 Deep Neural Network여야 하는가?
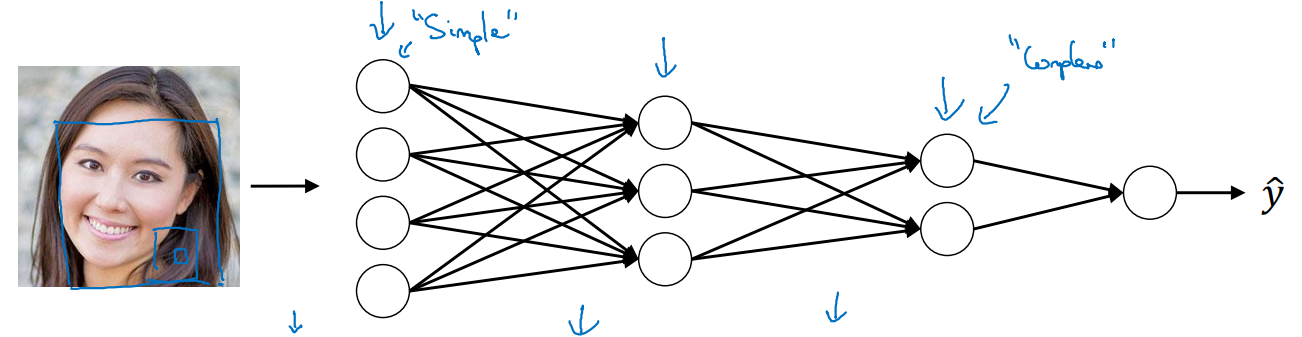
- 아래의 Input image를 Deep NN architecture에 집어 넣는다고 생각해 보자.
- 1st hidden layer가 추출할 수 있는 feature map은 다음 그림과 같다.
  - Vertical edge나 Horizontal edge와 같은 것들이 보인다.
  - 다소 simple한 특징들이지 않은가?
- 2nd hidden layer가 추출할 수 있는 feature map은 다음 그림과 같다.
  - 눈, 코, 입과 같은 특징들이 보인다.
  - 이전 layer에서 추출한 특징들보다는 좀 더 complex해 졌다.
- 3rd hidden layer가 추출할 수 있는 feature map은 다음 그림과 같다.
  - 이제는 사람 얼굴 형태로 추정할 수 있는 특징들이 많이 보인다.
  - layer를 깊게 쌓을 수록 추출할 수 있는 feature가 많아진다는 것을 알 수 있다.

Input 형태가 Audio일 때도 마찬가지다.
- Low level audio waveform
  → Phonemes(포님, 발음) : C A T
  → words
  → Sentence Phrase
  ...
- Deep layer NN일수록 더욱 complex한 문제들을 풀 수 있다!
  - Image detections, Audio detection ... etc.
Computational관점에서도 DeepNN이 효과적이다.
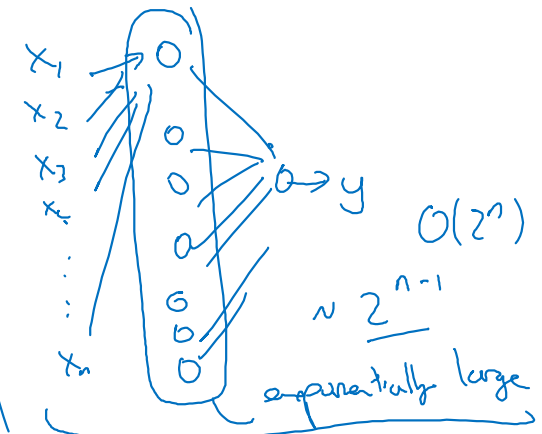
- 모든 Input $x$ 들에 대하여 XOR 연산을 n번 진행한다고 할 때,
  - 각 unit에서 XOR 연산이 일어난다고 보고,
  - n개의 units을 가지는 layer로 묶어 shallow하게 연산하게 되면,
    $O(2^{n-1})$ 의 계산 복잡도를 갖게 되어 상당히 비효율적이다.
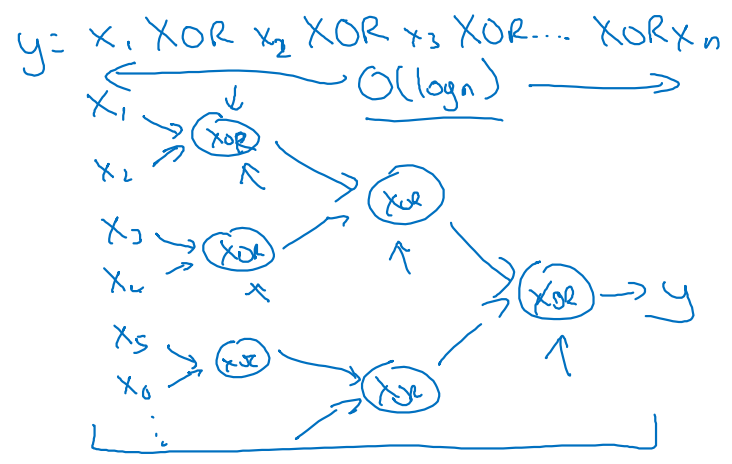
- 이를 Tree형태로 chain화하여 접근하게 되면
  - Deep하게 layer를 쌓는 과정과 유사해지며,
    $O(logn)$ 의 연산 속도를 갖게 되어 보다 효율적이다.

Building blocks of deep neural networks

DNN의 연산 과정은 Forward propagation과 Back propagation으로 이루어진다.
- 먼저 $l$ 번째 layer에서 일어나는 연산을 정리해보면 다음과 같다.
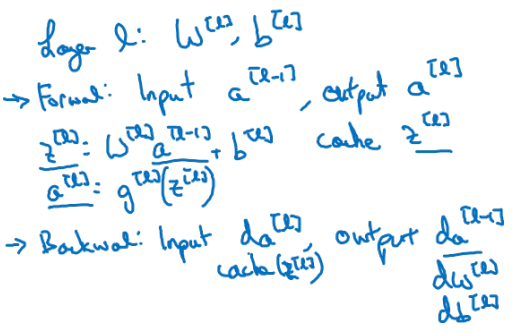
- 이 때, Forward에서 생성된 $a^{[l]}$ 와 $z^{[l]}$ 를 cache에 반드시 저장하여야 한다.
  - Backward에서 $da^{[l-1]}$ , $dW^{[l]}$ , $db^{[l]}$ 를 계산하기 위해 필요하기 때문이다.
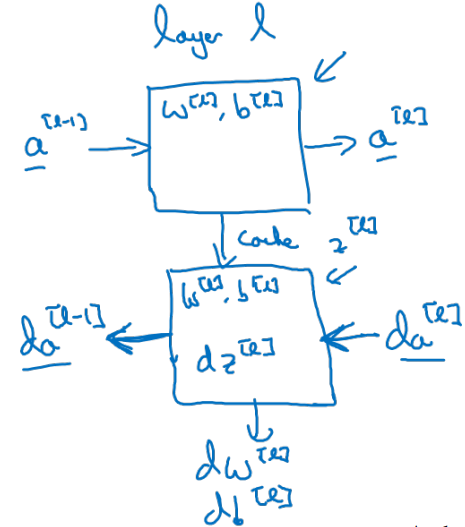
아래 그림은 $l$ th layer block에서 일어나는 연산 과정을 시각화 하였다.
전체적인 DNN 작동 process를 시각화 한 그림이다.
- Programming exercise에서 활용될 내용이다.

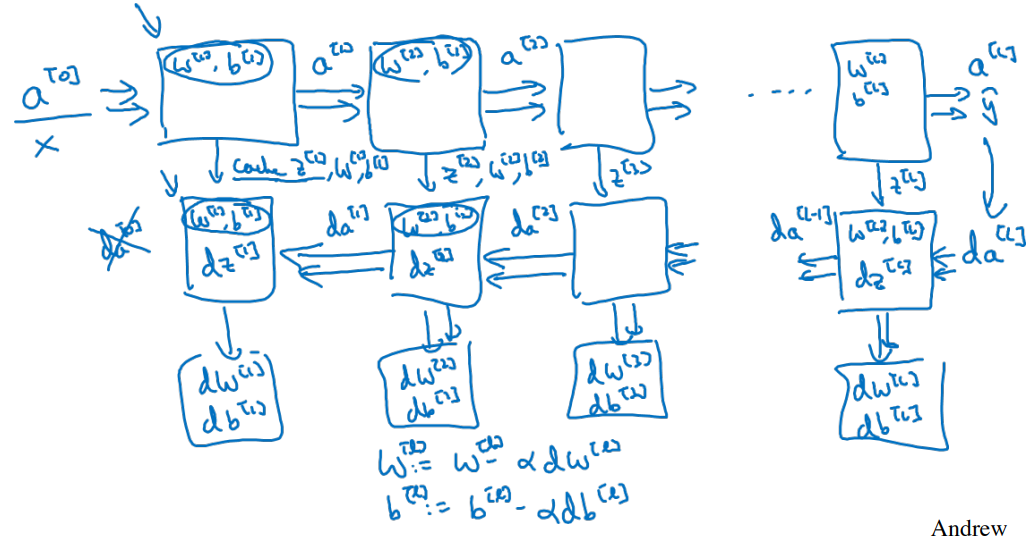
Forward and backward propagation

$l$ 번째 layer에서의 Forward와 Backward 연산 과정을 자세히 정리해보자.
- Forward propagation : Version of Vectorizal
  - $l-1$ 번째 layer의 output $A^{[l-1]}$ 을 받아 $l$ 번째 layer에서의 연산을 진행한다.
  - 이 때, $Z^{[l]}$ 는 cache에, activation $A^{[l]}$ 는 output에 저장한다.
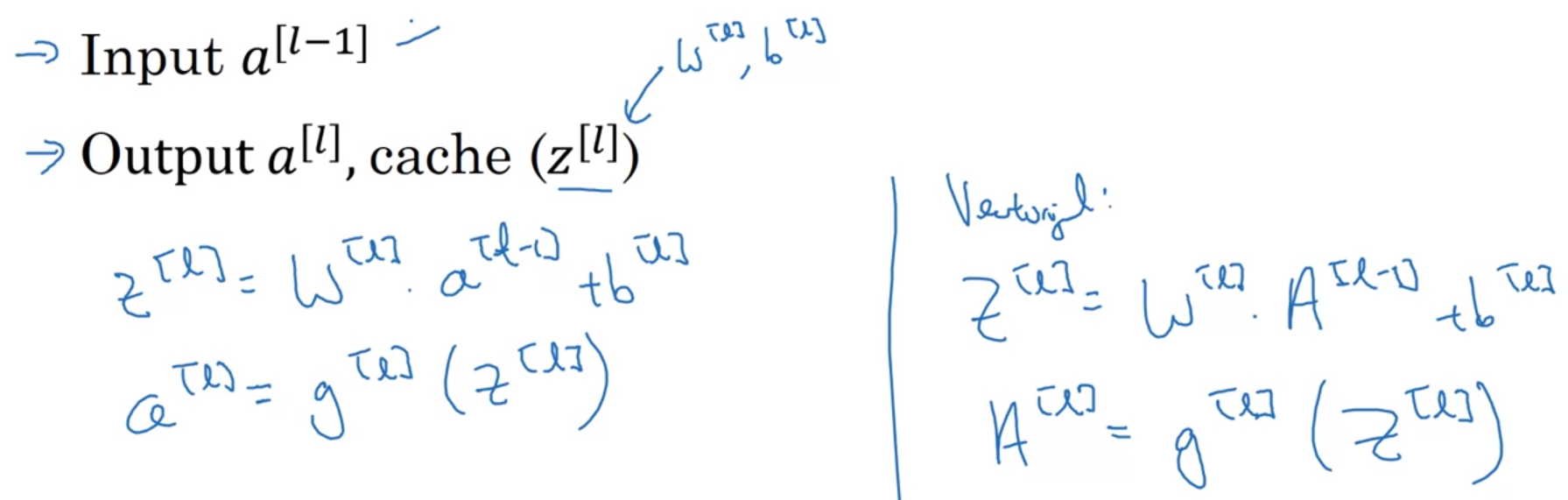
- Backward propagation : Version of Vectorizal
  - $l$ 번째 layer의 output $A^{[l]}$ 을 받아 $l-1$ 번째 layer에서의 연산을 진행한다.
  - 이 때, $l$ 번째 layer cache에 저장된 $Z^{[l]}$ 과 $l-1$ 번째 layer output $A^{[l-1]}$ 를 함께 활용하여 $dW^{[l]}$ 과 $db^{[l]}$ 를 계산할 수 있다!
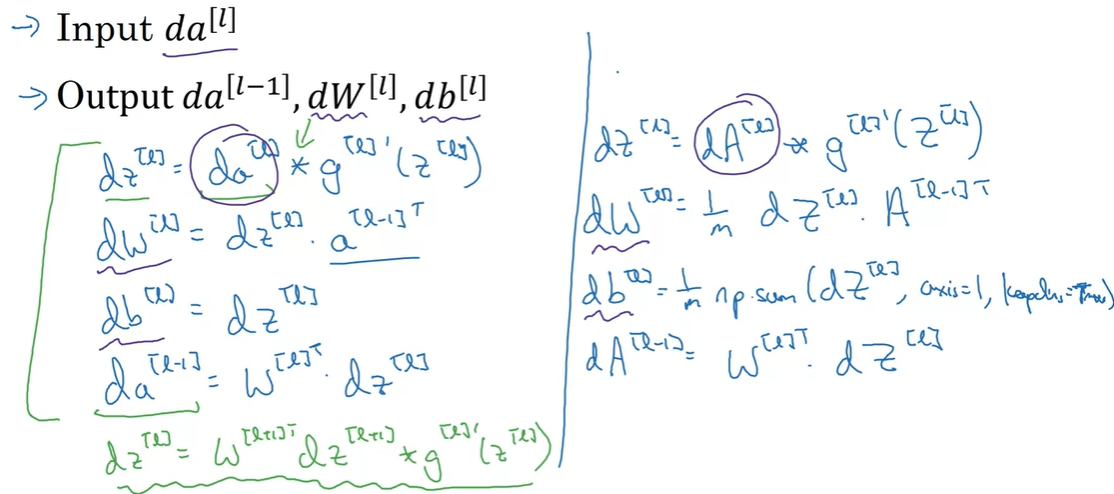
Summary
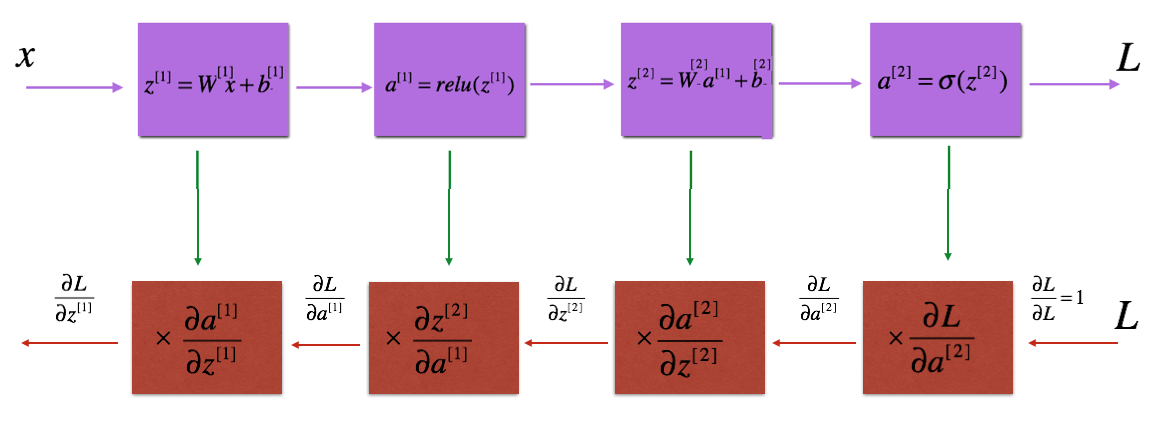
- 아래 그림은 하나의 unit에서 일어나는 forward와 backward propagation이다.
  - $da^{[l]}$ 는 한 training example로 loss의 미분값을 연산한 결과다.
  - $dA^{[l]}$ 로 표현된 Vectorizal version은 m개의 training examples의 loss 미분값을 더해서 표현한 derivative of Cost다.

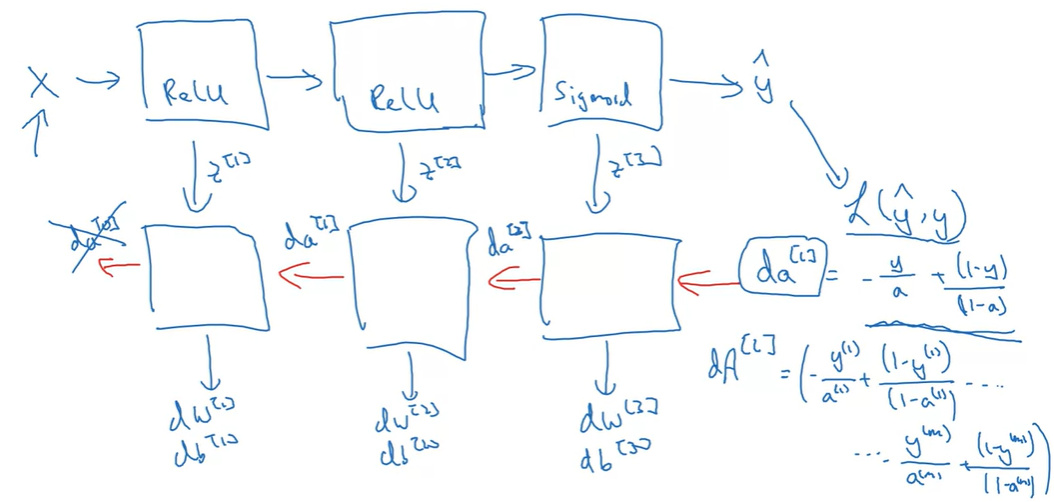
Parameters vs Hyperparameters

Hyperparameters는 Parameters를 control 할 수 있는 존재다.
- momentum, mimibatch size, regularization에서 설정하는 것들
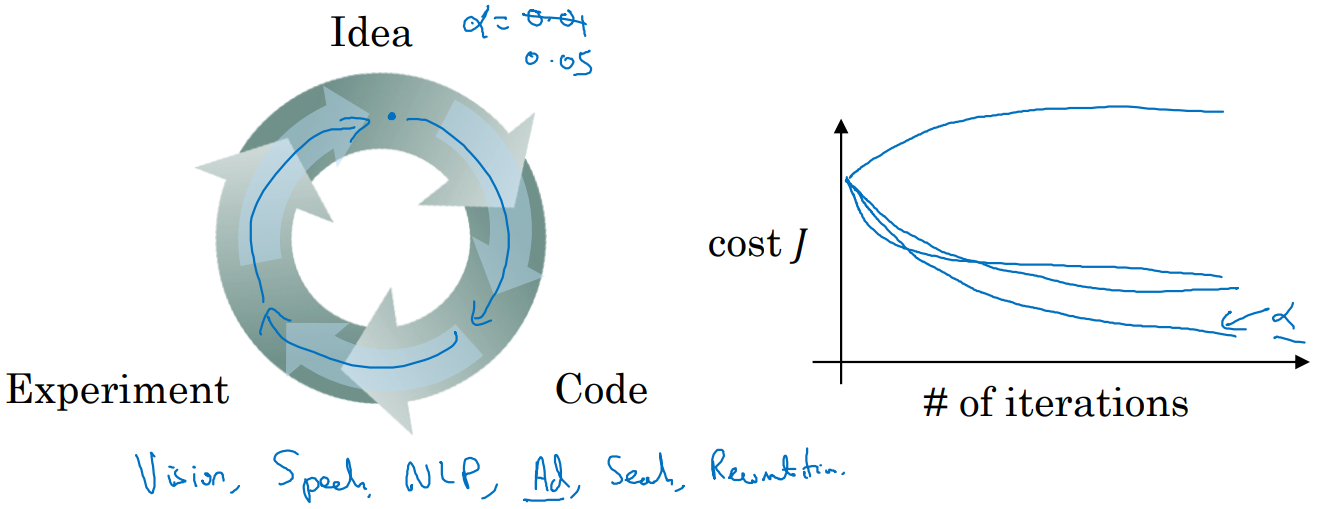
Deep Learning은 매우 empirical한 (경험적인) 과정이다.
- 어떤 hyperparameter를 설정했냐에 따라 결과가 크게 달라질 수 있다.
  - 따라서 Keep going Experiment 할 것.

What does this have to do with the brain?

Deep learning이 뇌의 정보 처리 과정과 닮았다는 사실은 Not a whole lot하다.
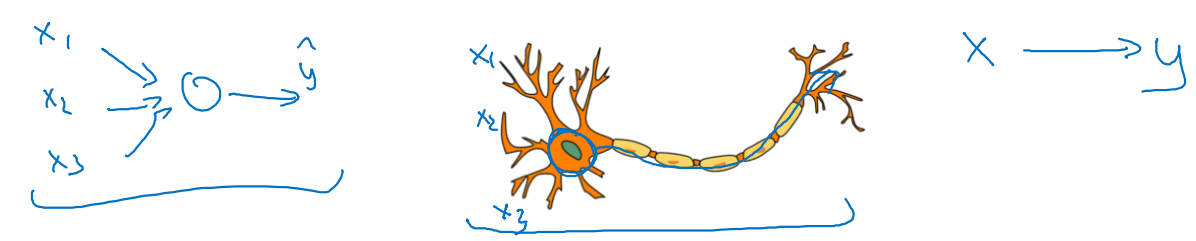
- Forward propagation은 뇌와 비슷하다고 여길만 했다.
  - 특히 CV 분야에서 뇌와 비슷하다고 여겼던 부분이 많았다.
- 허나 Backpropagation과정은 더 이상 뇌와 비슷하다고 여기기 힘들다.
  - 그러나 실제로 한 뉴런에서 어떤 일이 일어나는지는 밝혀지지 않았다.
결론: Deep learning은 $X → y$ 로 mapping하는 과정이라고 보자.

Assignment

W4A1

Building your Deep Neural Network: Step by Step

2-layer Neural Network
- Initialize parameters: random * 0.01

def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- size of the input layer
    n_h -- size of the hidden layer
    n_y -- size of the output layer
    
    Returns:
    parameters -- python dictionary containing your parameters:
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape (n_y, 1)
    """
    
    np.random.seed(1)

    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

L-layer Neural Network
- Initialize parameters deep: 1~L까지의 $l$ th layer

def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the dimensions of each layer in our network
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    bl -- bias vector of shape (layer_dims[l], 1)
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims) # number of layers in the network

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01  # [2, 4(l), 1]
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
        
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))

        
    return parameters

Linear forward $Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}$ where $A^{[0]} = X$ .

def linear_forward(A, W, b):
    """
    Implement the linear part of a layer's forward propagation.

    Arguments:
    A -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)

    Returns:
    Z -- the input of the activation function, also called pre-activation parameter 
    cache -- a python tuple containing "A", "W" and "b" ; stored for computing the backward pass efficiently
    """

    Z = np.dot(W, A) + b
    cache = (A, W, b)
    
    return Z, cache

Linear activation forward
- Sigmoid: $\sigma(Z) = \sigma(W A + b) = \displaystyle \frac{1}{ 1 + e^{-(W A + b)}}$
- ReLU: $A = ReLU(Z) = max(0, Z)$
- $A^{[l]} = g(Z^{[l]}) = g(W^{[l]}A^{[l-1]} +b^{[l]})$
  
  where the activation " $g$ " can be sigmoid() or relu().

def linear_activation_forward(A_prev, W, b, activation):
    """
    Implement the forward propagation for the LINEAR->ACTIVATION layer

    Arguments:
    A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"

    Returns:
    A -- the output of the activation function, also called the post-activation value 
    cache -- a python tuple containing "linear_cache" and "activation_cache";
             stored for computing the backward pass efficiently
    """
    
    if activation == "sigmoid":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)  # maybe : sigmoid, cache -> dict
    
    elif activation == "relu":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)  # cache = (linear_cache, activation_cache)

    cache = (linear_cache, activation_cache)

    return A, cache

L-Layer Model
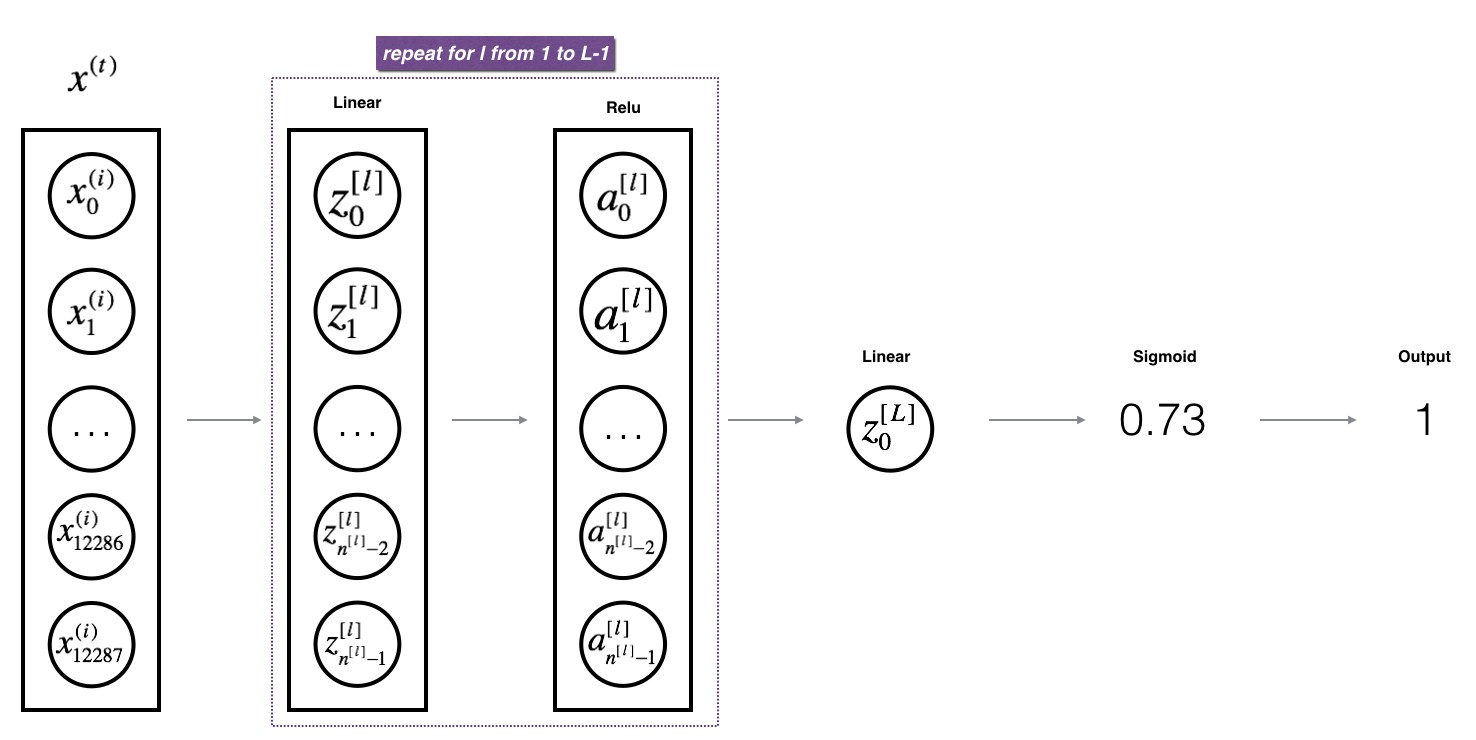
L model forward
- 1 ~ L-1 : ReLU forward
- L : Sigmoid forward
$A^{[L]} = \sigma(Z^{[L]}) = \sigma(W^{[L]} A^{[L-1]} + b^{[L]})$

def L_model_forward(X, parameters):
    """
    Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
    
    Arguments:
    X -- data, numpy array of shape (input size, number of examples)
    parameters -- output of initialize_parameters_deep()
    
    Returns:
    AL -- activation value from the output (last) layer
    caches -- list of caches containing:
                every cache of linear_activation_forward() (there are L of them, indexed from 0 to L-1)
    """

    caches = []
    A = X
    L = len(parameters) // 2 # divided by (W, b) # number of layers in the neural network
    
    # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
    # The for loop starts at 1 because layer 0 is the input
    for l in range(1, L):  # startswith 1
        A_prev = A  # update
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation='relu')
        caches.append(cache)  # startswith 0i
    
    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation='sigmoid')
    caches.append(cache)  
          
    return AL, caches

Cost function
$-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right))$

def compute_cost(AL, Y):
    """
    Implement the cost function defined by equation (7).

    Arguments:
    AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
    Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)

    Returns:
    cost -- cross-entropy cost
    """
    
    m = Y.shape[1]

    cost = -1/m * (np.dot(np.log(AL), Y.T) + np.dot(np.log(1-AL), (1-Y.T)))
    
    cost = np.squeeze(cost)  # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).

    return cost

Backward Propagation Module
Linear backward

dW^{[l]} = \frac{\partial \mathcal{J} }{\partial W^{[l]}} = \frac{1}{m} dZ^{[l]} A^{[l-1] T}

db^{[l]} = \frac{\partial \mathcal{J} }{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}

dA^{[l-1]} = \frac{\partial \mathcal{L} }{\partial A^{[l-1]}} = W^{[l] T} dZ^{[l]}

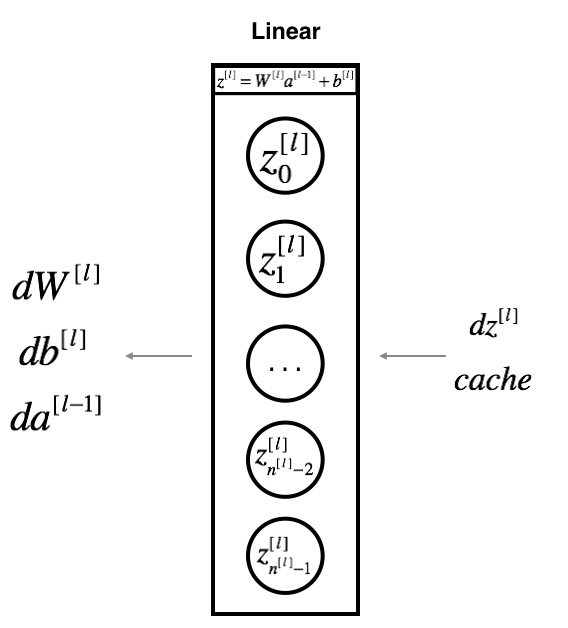
def linear_backward(dZ, cache):
    """
    Implement the linear portion of backward propagation for a single layer (layer l)

    Arguments:
    dZ -- Gradient of the cost with respect to the linear output (of current layer l)
    cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer

    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW -- Gradient of the cost with respect to W (current layer l), same shape as W
    db -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = 1/m * np.dot(dZ, A_prev.T)
    db = 1/m * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)
    
    return dA_prev, dW, db

Linear activation backward

$dZ^{[l]} = dA^{[l]} * g'(Z^{[l]})$
- First, define relu & sigmoid backward
- Second, define linear activation backward

def relu_backward(dA, cache):
    """
    Implement the backward propagation for a single RELU unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    
    Z = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.
    
    # When z <= 0, you should set dz to 0 as well. 
    dZ[Z <= 0] = 0
    
    assert (dZ.shape == Z.shape)
    
    return dZ

def sigmoid_backward(dA, cache):
    """
    Implement the backward propagation for a single SIGMOID unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    
    Z = cache
    
    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)
    
    assert (dZ.shape == Z.shape)
    
    return dZ


def linear_activation_backward(dA, cache, activation):
    """
    Implement the backward propagation for the LINEAR->ACTIVATION layer.
    
    Arguments:
    dA -- post-activation gradient for current layer l 
    cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
    
    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW -- Gradient of the cost with respect to W (current layer l), same shape as W
    db -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    linear_cache, activation_cache = cache
    
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)  # dA * g'(Z)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
        
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)  # activation_cache
        dA_prev, dW, db = linear_backward(dZ, linear_cache)  # linear_cache

    return dA_prev, dW, db

L model backward
- L-1 : Sigmoid backward
- L-2 ~ 0 : ReLU backward
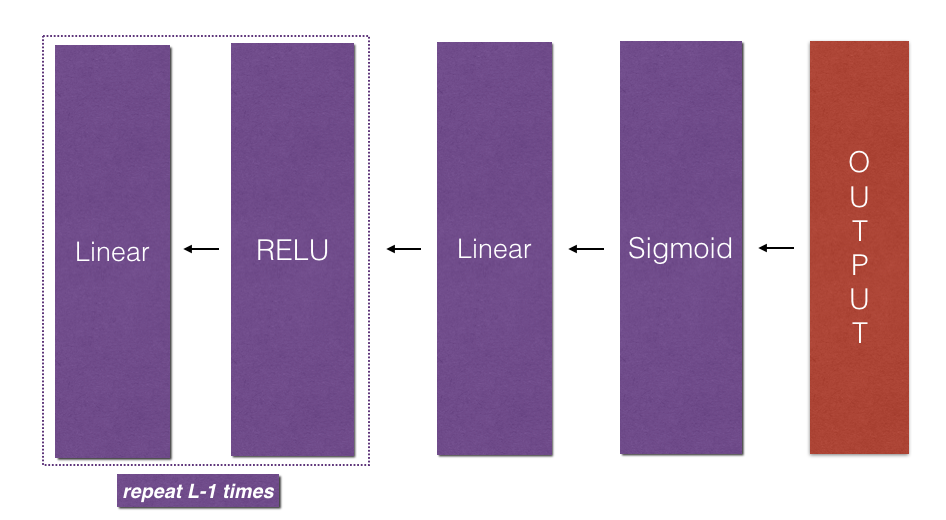
$dA^{[L]} = - (\displaystyle \frac{Y}{A^{[L]}} - \displaystyle \frac{1-Y}{1-A^{[L]}})$

def L_model_backward(AL, Y, caches):
    """
    Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
    
    Arguments:
    AL -- probability vector, output of the forward propagation (L_model_forward())
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
    caches -- list of caches containing:
                every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
                the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])
    
    Returns:
    grads -- A dictionary with the gradients
             grads["dA" + str(l)] = ... 
             grads["dW" + str(l)] = ...
             grads["db" + str(l)] = ... 
    """
    grads = {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
    
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) # derivative of cost with respect to AL
    
    # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "dAL, current_cache". Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"]
    current_cache = caches[-1]
    dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dAL, current_cache, activation='sigmoid')
    grads['dA' + str(L-1)] = dA_prev_temp
    grads['dW' + str(L)] = dW_temp
    grads['db' + str(L)] = db_temp
    
    # Loop from l=L-2 to l=0
    for l in reversed(range(L-1)):
        # lth layer: (RELU -> LINEAR) gradients.
        # Inputs: "grads["dA" + str(l + 1)], current_cache". Outputs: "grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)] 
        current_cache = caches[l]  # L-1, ...
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dA_prev_temp, current_cache, activation='relu')
        grads['dA' + str(l)] = dA_prev_temp
        grads['dW' + str(l+1)] = dW_temp
        grads['db' + str(l+1)] = db_temp

    return grads

Update parameters
$W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]}$ $b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]}$

def update_parameters(params, grads, learning_rate):
    """
    Update parameters using gradient descent
    
    Arguments:
    params -- python dictionary containing your parameters 
    grads -- python dictionary containing your gradients, output of L_model_backward
    
    Returns:
    parameters -- python dictionary containing your updated parameters 
                  parameters["W" + str(l)] = ... 
                  parameters["b" + str(l)] = ...
    """
    parameters = copy.deepcopy(params)
    L = len(parameters) // 2 # number of layers in the neural network

    # Update rule for each parameter. Use a for loop.
    for l in range(L):
        parameters['W' + str(l+1)] -= learning_rate * grads['dW' + str(l+1)]
        parameters['b' + str(l+1)] -= learning_rate * grads['db' + str(l+1)]

    return parameters

W4A2

Deep Neural Network for Image Classification: Application

Load and Process the Dataset

def load_data():
    train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels

    test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels

    classes = np.array(test_dataset["list_classes"][:]) # the list of classes
    
    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
    
    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes


train_x_orig, train_y, test_x_orig, test_y, classes = load_data()

Number of training examples: 209
Number of testing examples: 50
Each image is of size: (64, 64, 3)
train_x_orig shape: (209, 64, 64, 3)
train_y shape: (1, 209)
test_x_orig shape: (50, 64, 64, 3)
test_y shape: (1, 50)

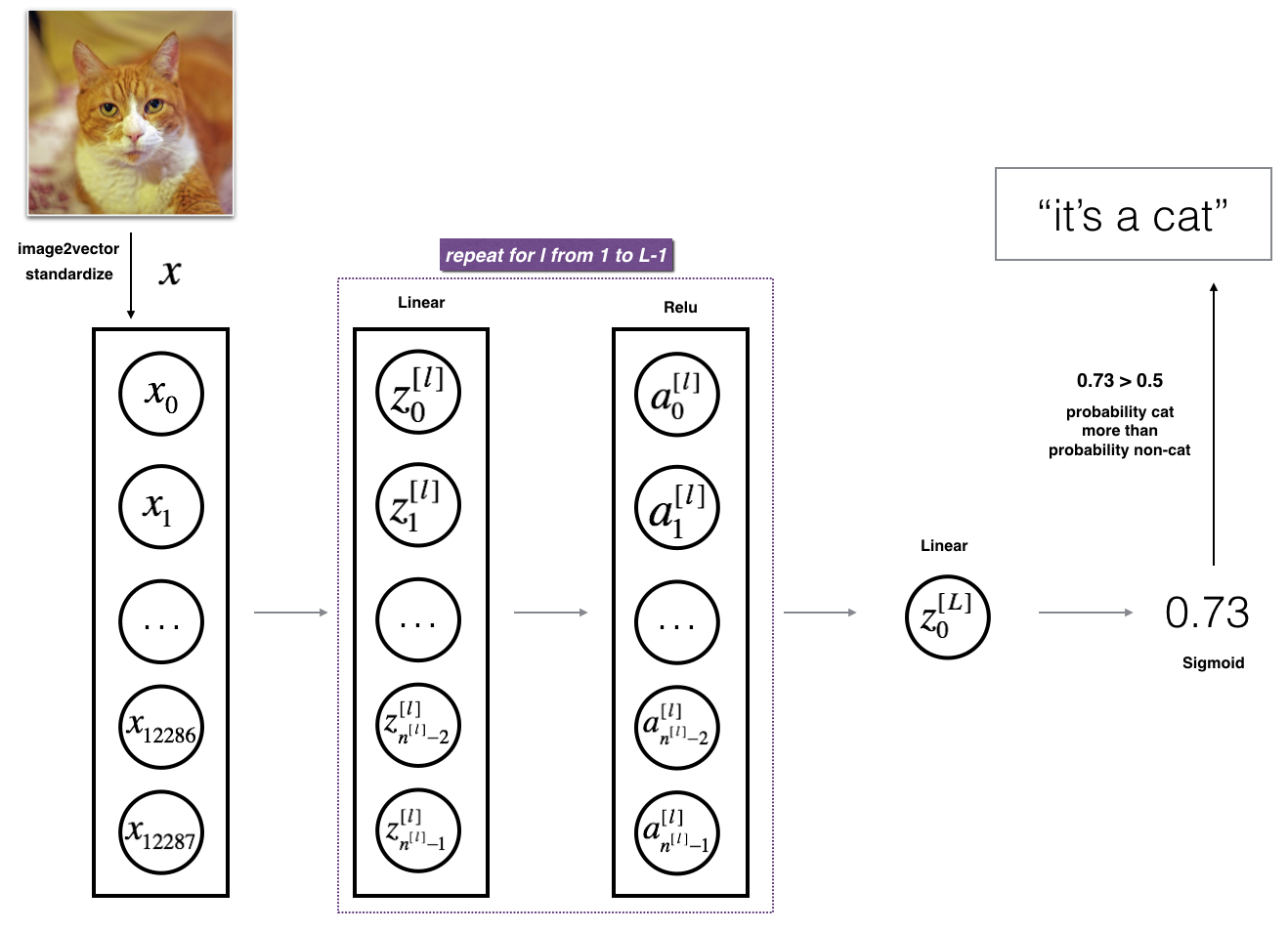
Image2Vector conversion

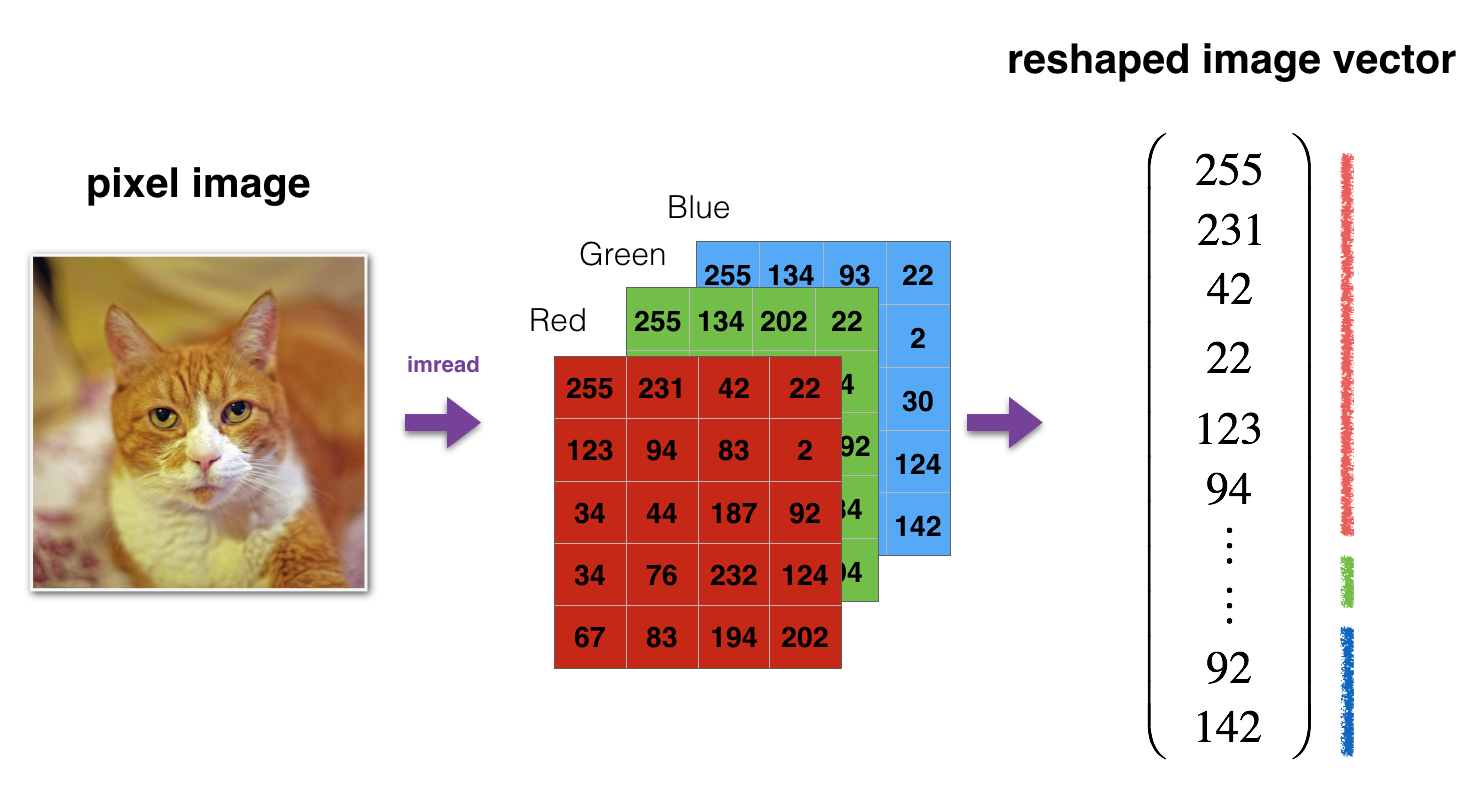
# Reshape the training and test examples 
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T   # The "-1" makes reshape flatten the remaining dimensions
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T

# Standardize data to have feature values between 0 and 1.
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.

train_x's shape: (12288, 209)
test_x's shape: (12288, 50)

2-layer Neural Network

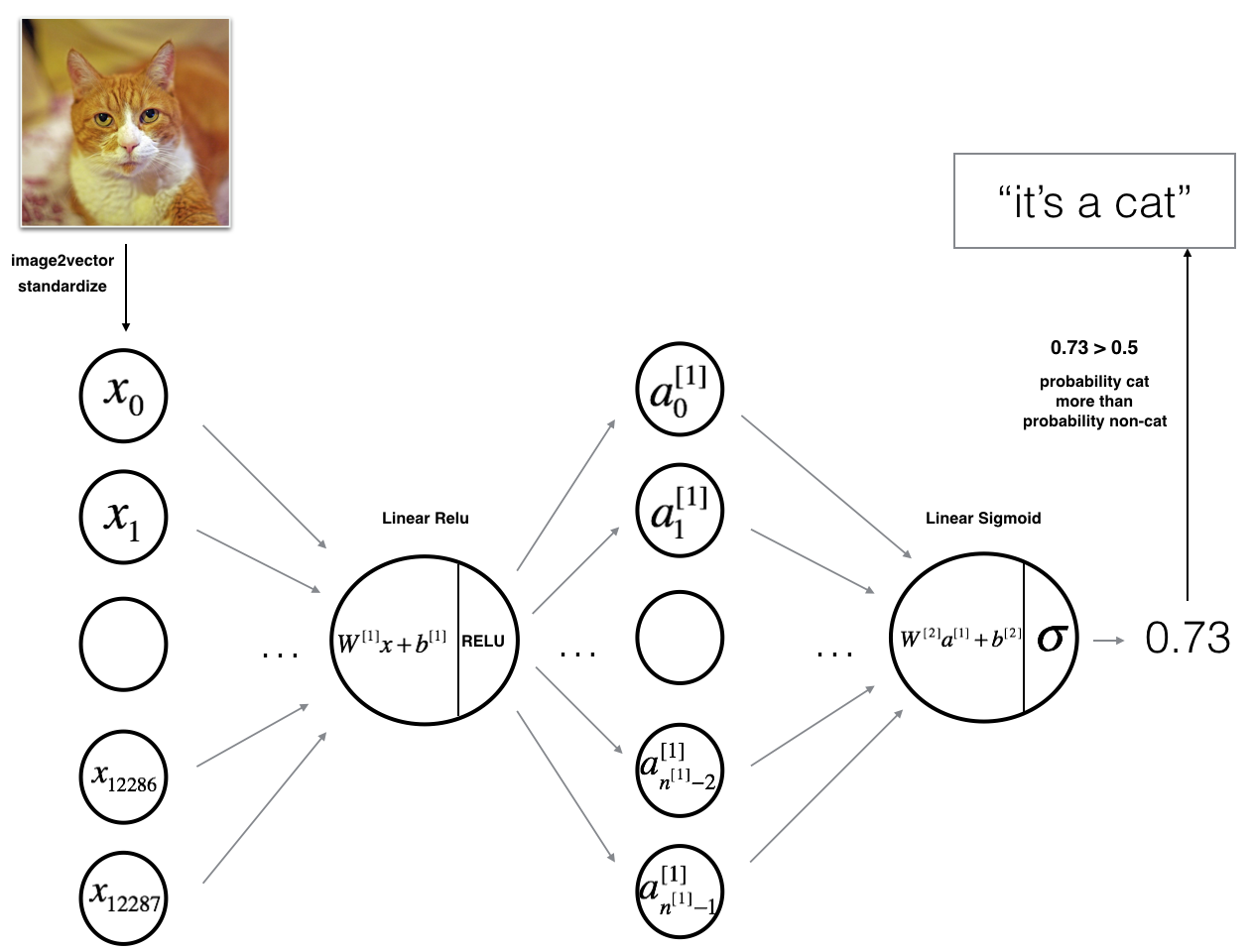
def initialize_parameters(n_x, n_h, n_y):
    ...
    return parameters 
def linear_activation_forward(A_prev, W, b, activation):
    ...
    return A, cache
def compute_cost(AL, Y):
    ...
    return cost
def linear_activation_backward(dA, cache, activation):
    ...
    return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters

2-layer model Architecture

def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    """
    Implements a two-layer neural network: LINEAR->RELU->LINEAR->SIGMOID.
    
    Arguments:
    X -- input data, of shape (n_x, number of examples)
    Y -- true "label" vector (containing 1 if cat, 0 if non-cat), of shape (1, number of examples)
    layers_dims -- dimensions of the layers (n_x, n_h, n_y)
    num_iterations -- number of iterations of the optimization loop
    learning_rate -- learning rate of the gradient descent update rule
    print_cost -- If set to True, this will print the cost every 100 iterations 
    
    Returns:
    parameters -- a dictionary containing W1, W2, b1, and b2
    """
    
    np.random.seed(1)
    grads = {}
    costs = []                              # to keep track of the cost
    m = X.shape[1]                           # number of examples
    (n_x, n_h, n_y) = layers_dims
    
    # Initialize parameters dictionary, by calling one of the functions you'd previously implemented
    parameters = initialize_parameters(n_x, n_h, n_y)
    
    # Get W1, b1, W2 and b2 from the dictionary parameters.
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # Loop (gradient descent)
    for i in range(0, num_iterations):

        # Forward propagation: LINEAR -> RELU -> LINEAR -> SIGMOID. Inputs: "X, W1, b1, W2, b2". Output: "A1, cache1, A2, cache2".
        A1, cache1 = linear_activation_forward(X, W1, b1, activation='relu')
        A2, cache2 = linear_activation_forward(A1, W2, b2, activation='sigmoid')
        
        # Compute cost
        cost = compute_cost(A2, Y)
        
        # Initializing backward propagation
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        
        # Backward propagation. Inputs: "dA2, cache2, cache1". Outputs: "dA1, dW2, db2; also dA0 (not used), dW1, db1".
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, activation='sigmoid')
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, activation='relu')
        
        # Set grads['dWl'] to dW1, grads['db1'] to db1, grads['dW2'] to dW2, grads['db2'] to db2
        grads['dW1'] = dW1
        grads['db1'] = db1
        grads['dW2'] = dW2
        grads['db2'] = db2
        
        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)

        # Retrieve W1, b1, W2, b2 from parameters
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]
        
        # Print the cost every 100 iterations
        if print_cost and i % 100 == 0 or i == num_iterations - 1:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if i % 100 == 0 or i == num_iterations:
            costs.append(cost)

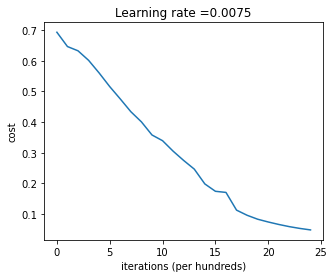
    return parameters, costs

Train 2-layer model

def plot_costs(costs, learning_rate=0.0075):
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()

parameters, costs = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)
plot_costs(costs, learning_rate)

>>> Cost after iteration 0: 0.693049735659989
	Cost after iteration 100: 0.6464320953428849
	Cost after iteration 200: 0.6325140647912677
	Cost after iteration 300: 0.6015024920354665
	Cost after iteration 400: 0.5601966311605747
	...

Prediction

def predict(X, y, parameters):
    """
    This function is used to predict the results of a  L-layer neural network.
    
    Arguments:
    X -- data set of examples you would like to label
    parameters -- parameters of the trained model
    
    Returns:
    p -- predictions for the given dataset X
    """
    
    m = X.shape[1]
    n = len(parameters) // 2 # number of layers in the neural network
    p = np.zeros((1,m))
    
    # Forward propagation
    probas, caches = L_model_forward(X, parameters)

    # convert probas to 0/1 predictions
    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0
    
    print("Accuracy: "  + str(np.sum((p == y)/m)))
        
    return p

predictions_train = predict(train_x, train_y, parameters)
>>> Accuracy: 0.9999999999999998

predictions_train = predict(test_x, test_y, parameters)
>>> Accuracy: 0.72

L-layer Deep Neural Network

def initialize_parameters_deep(layers_dims):
    ...
    return parameters 
def L_model_forward(X, parameters):
    ...
    return AL, caches
def compute_cost(AL, Y):
    ...
    return cost
def L_model_backward(AL, Y, caches):
    ...
    return grads
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters

### CONSTANTS ###
layers_dims = [12288, 20, 7, 5, 1] #  4-layer model

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    """
    Implements a L-layer neural network: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
    
    Arguments:
    X -- input data, of shape (n_x, number of examples)
    Y -- true "label" vector (containing 1 if cat, 0 if non-cat), of shape (1, number of examples)
    layers_dims -- list containing the input size and each layer size, of length (number of layers + 1).
    learning_rate -- learning rate of the gradient descent update rule
    num_iterations -- number of iterations of the optimization loop
    print_cost -- if True, it prints the cost every 100 steps
    
    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    np.random.seed(1)
    costs = []                         # keep track of cost
    
    # Parameters initialization.
    parameters = initialize_parameters_deep(layers_dims)
    
    # Loop (gradient descent)
    for i in range(0, num_iterations):

        # Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
        AL, caches = L_model_forward(X, parameters)
        
        # Compute cost.
        cost = compute_cost(AL, Y)
    
        # Backward propagation.
        grads = L_model_backward(AL, Y, caches)
 
        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)
                
        # Print the cost every 100 iterations
        if print_cost and i % 100 == 0 or i == num_iterations - 1:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if i % 100 == 0 or i == num_iterations:
            costs.append(cost)
    
    return parameters, costs

Train L-layer model

parameters, costs = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)

>>> Cost after iteration 0: 0.7717493284237686
	Cost after iteration 100: 0.6720534400822914
	Cost after iteration 200: 0.6482632048575212
	Cost after iteration 300: 0.6115068816101356
	Cost after iteration 400: 0.5670473268366111
	...

Prediction

pred_train = predict(train_x, train_y, parameters)
>>> Accuracy: 0.9856459330143539

pred_train = predict(test_x, test_y, parameters)
>>> Accuracy: 0.8

Result analysis
- Print misabled!

def print_mislabeled_images(classes, X, y, p):
    """
    Plots images where predictions and truth were different.
    X -- dataset
    y -- true labels
    p -- predictions
    """
    a = p + y  # 0+1 or 1+0
    mislabeled_indices = np.asarray(np.where(a == 1))  # [[행 인덱스s], [열 인덱스s]]
    plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
    num_images = len(mislabeled_indices[0])
    for i in range(num_images):
        index = mislabeled_indices[1][i]  # [행][열]
        
        plt.subplot(2, num_images, i + 1)
        plt.imshow(X[:,index].reshape(64,64,3), interpolation='nearest')
        plt.axis('off')
        plt.title("Prediction: " + classes[int(p[0,index])].decode("utf-8") + " \n Class: " + classes[y[0,index]].decode("utf-8"))

print_mislabeled_images(classes, test_x, test_y, pred_test)