[MMD] Calculus for Machine Learning and Data Science Week 3
Week 3 - Optimization in Neural Networks and Newton's Method
Lesson 1 - Optimization in Neural Networks
Regression with a perceptron
-
House size를 통해 price를 예측하는 task가 주어졌다고 해보자.
- 눈치챘겠지만 두 변수의 관계를 linear regression으로 정의하고자 하는 것이다.

-
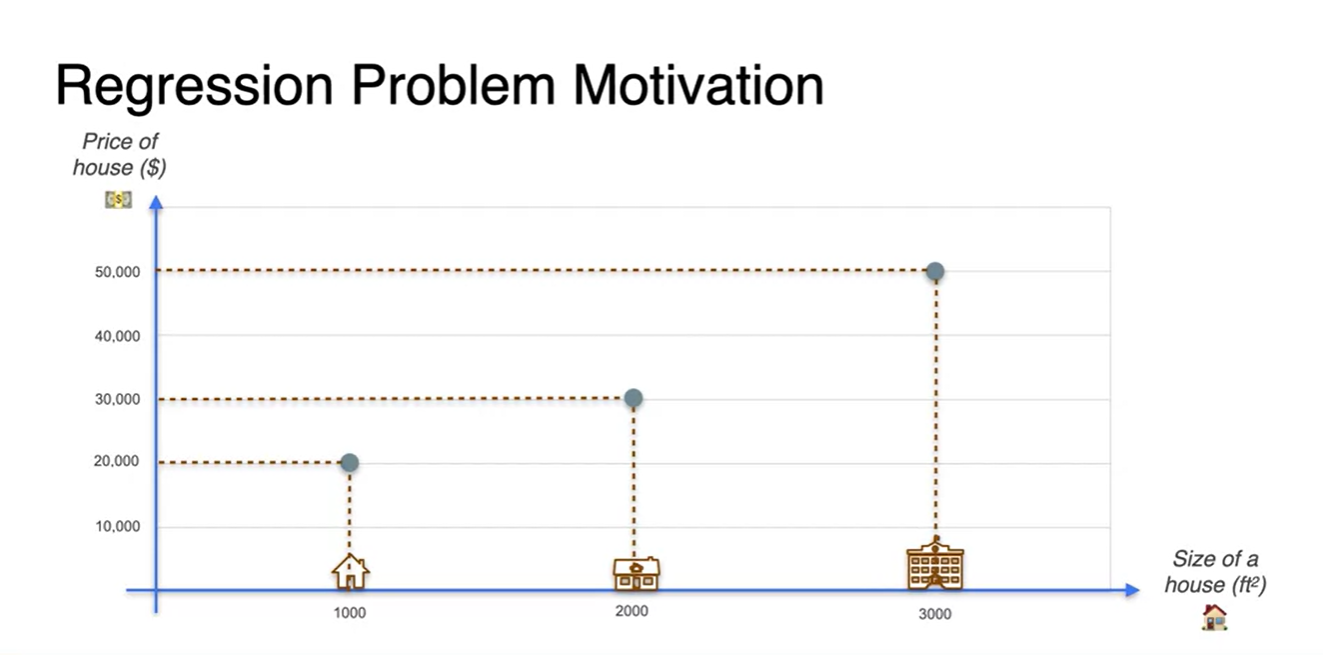
3개의 data point가 주어진 상황에서 둘의 관계를 예측해보자.
- 아마도 size가 n배 늘어남에 따라 price도 n배 늘어나는 완전한 선형 관계를 가진다고 추측할 수 있다.
-
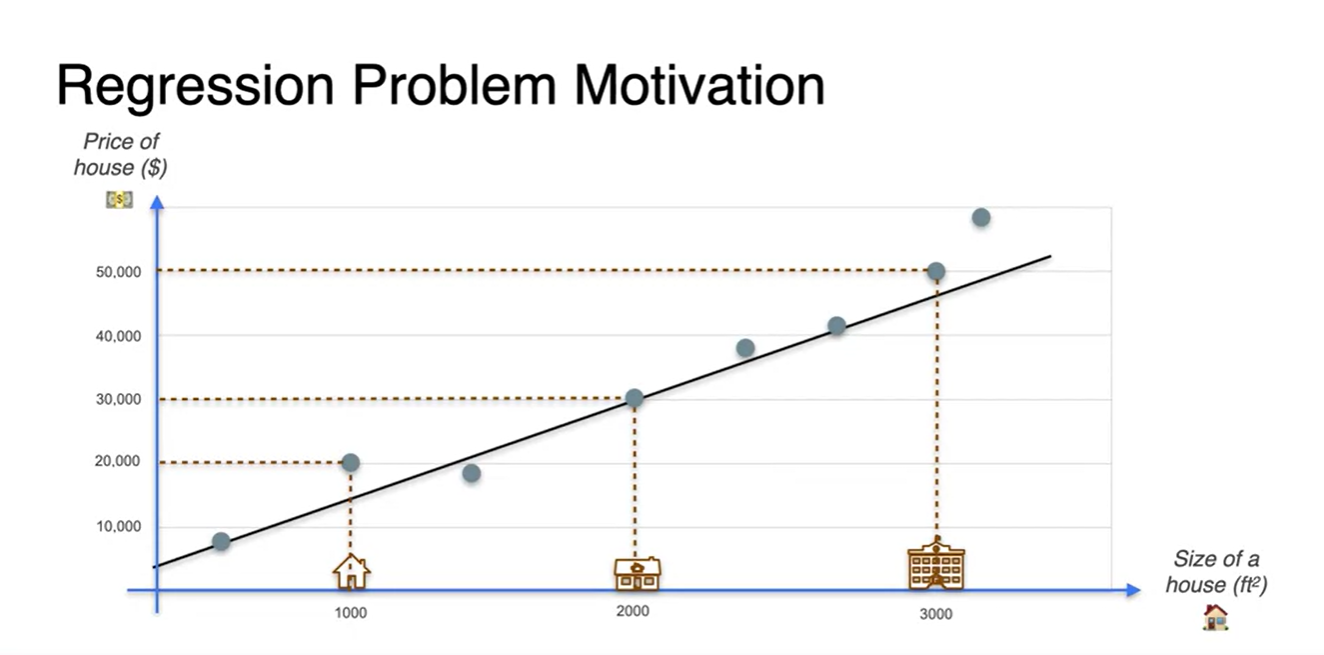
그러나 data point가 많아지고 완전한 선형성이 깨진다면
- 모든 data point의 선형 관계를 아우르는 최적의 선형 방정식을 찾아야만 한다.
-
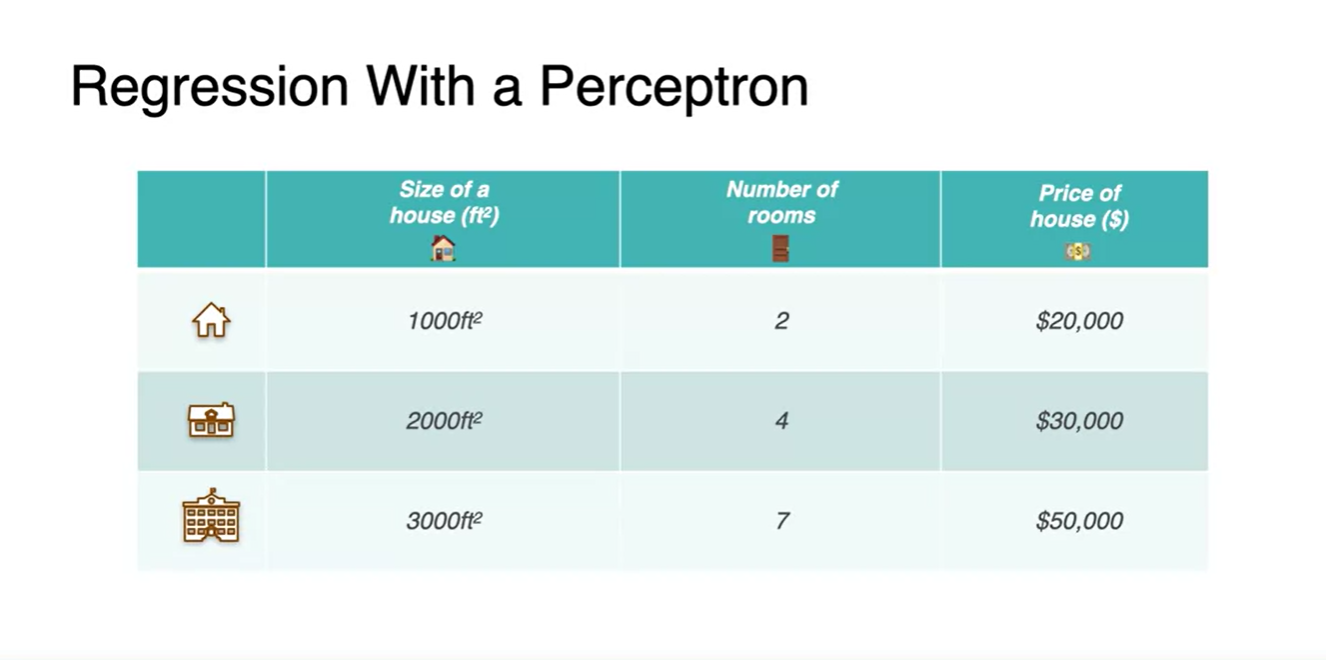
위의 data에서 room의 개수까지 관계 변수로 추가한 표(행렬)를 나타내면 아래와 같다.
- 우리가 머신러닝에서 행해야 할 data format은 행렬 batch이므로 이 틀을 잘 기억해두자.
-
하나의 변수 뿐만 아니라 여러 변수에 영향을 받는 선형 관계를 예측하고자 한다면
-
Input은 size와 room의 개수가 m개의 training set으로 담긴 행렬 (row 기준)
- 즉, shape이 (2, m)인 data
-
Output은 m개의 training set을 예측한 price 행렬
- 즉, shape이 (1, m) == (m,)인 data가 된다.
-

-
Regression의 추론 과정은 각 data point들을 Summation function에 넘겨 mapping하고
- 추론값 을 예측하여 실제 정답과 비교하도록 하는 과정이다.
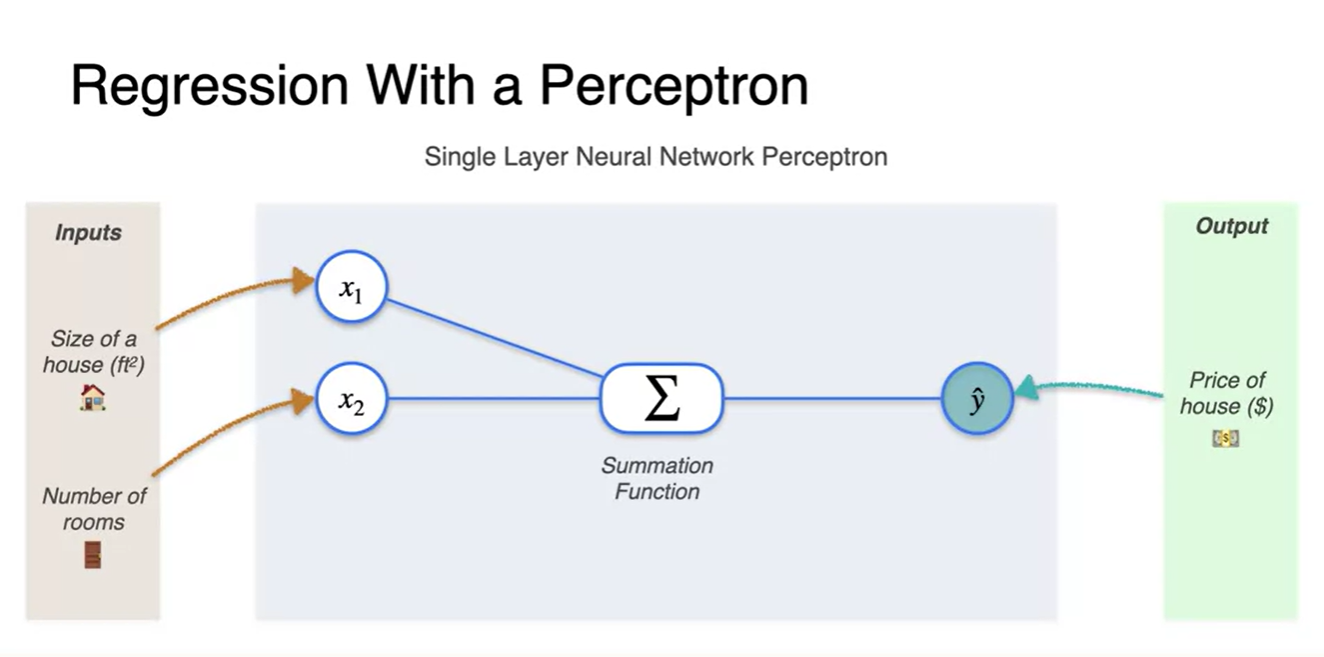
-
Summation function의 전체적인 수식은 로 표현되며
- Linear transform + bias 또는 단순 Affine transform이라 부른다.
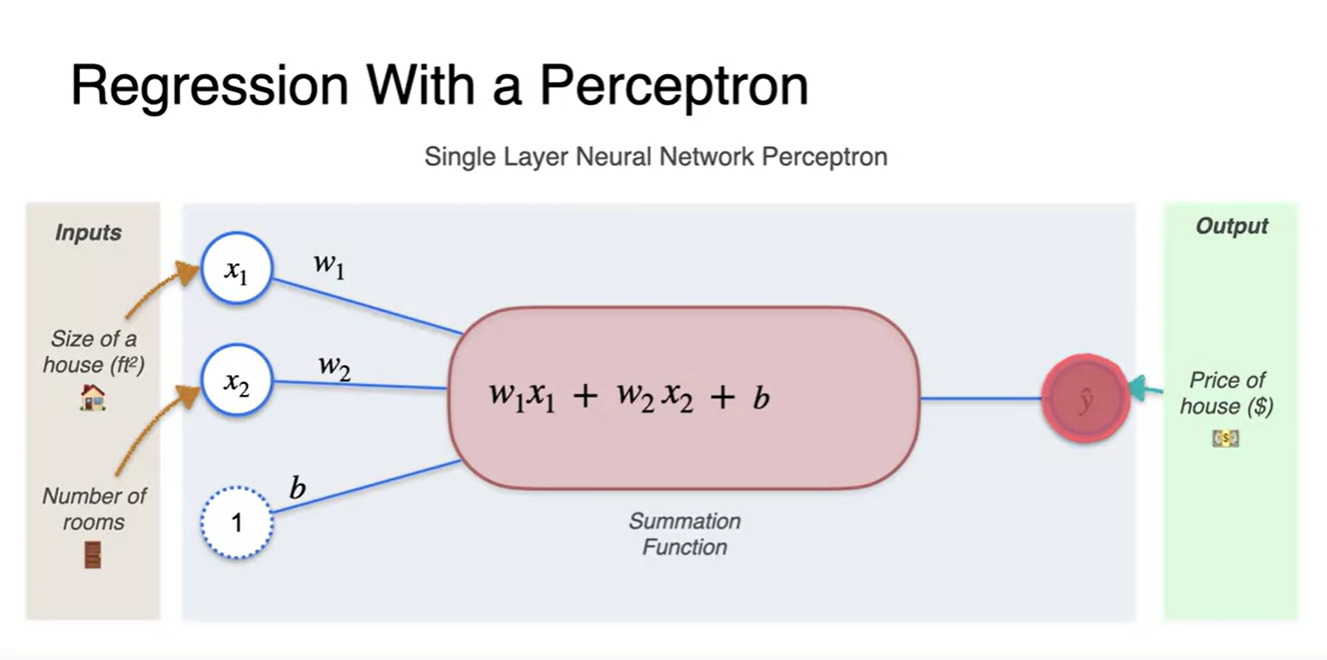
-
주의해야 할 점은 우리가 찾는 변수 즉, 업데이트 되는 값은 나 가 아니라는 점이다.
-
우리는 가중치와 편향 parameter 와 를 업데이트 하는 것이다.
- 앞서 배웠던 Loss function을 이용하여 data point들의 관계성을 가장 잘 나타내는 parameter를 추정하는 과정을 거칠 것이다.
-
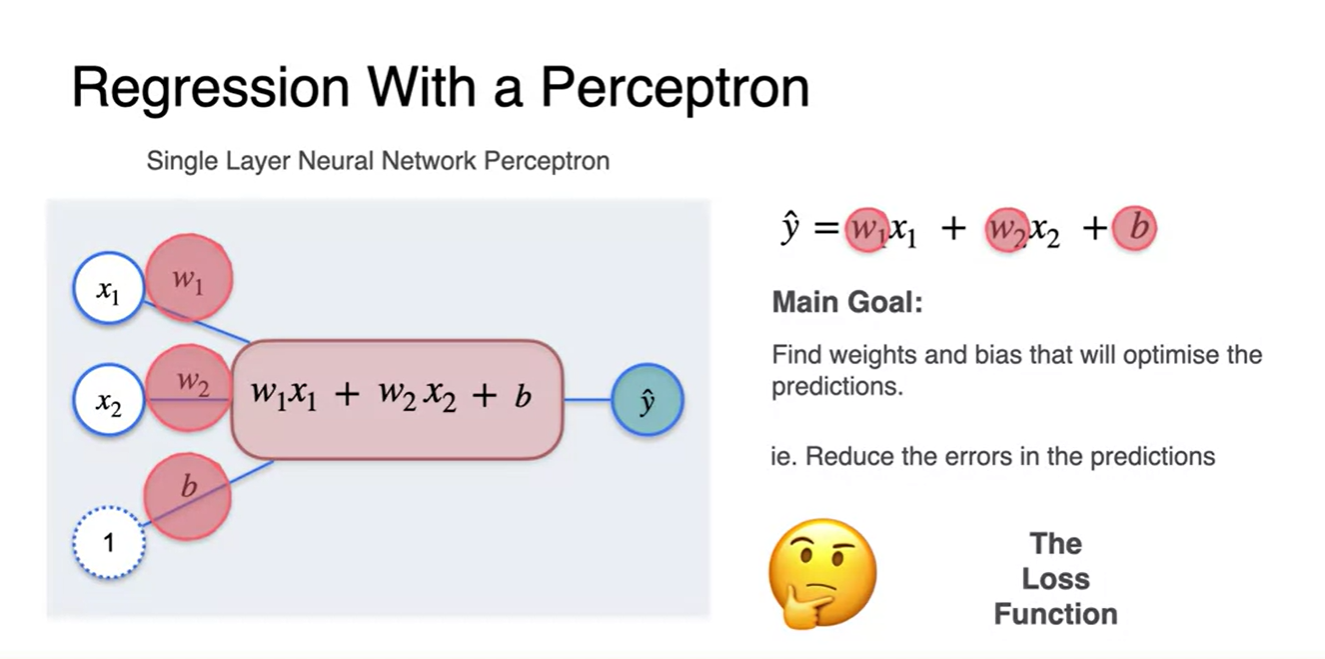
Regression with a perceptron - Loss function
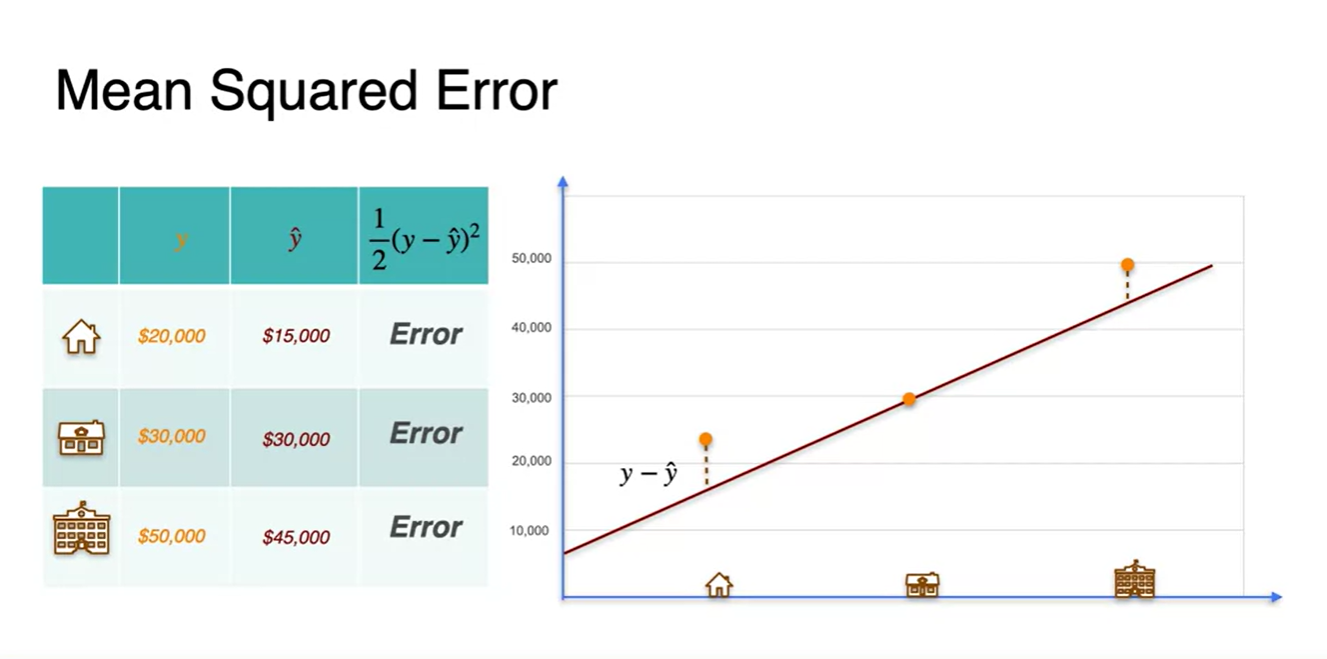
- 우리는 실제 정답 와 추론값 의 차이를 Error라고 정의할 수 있다.
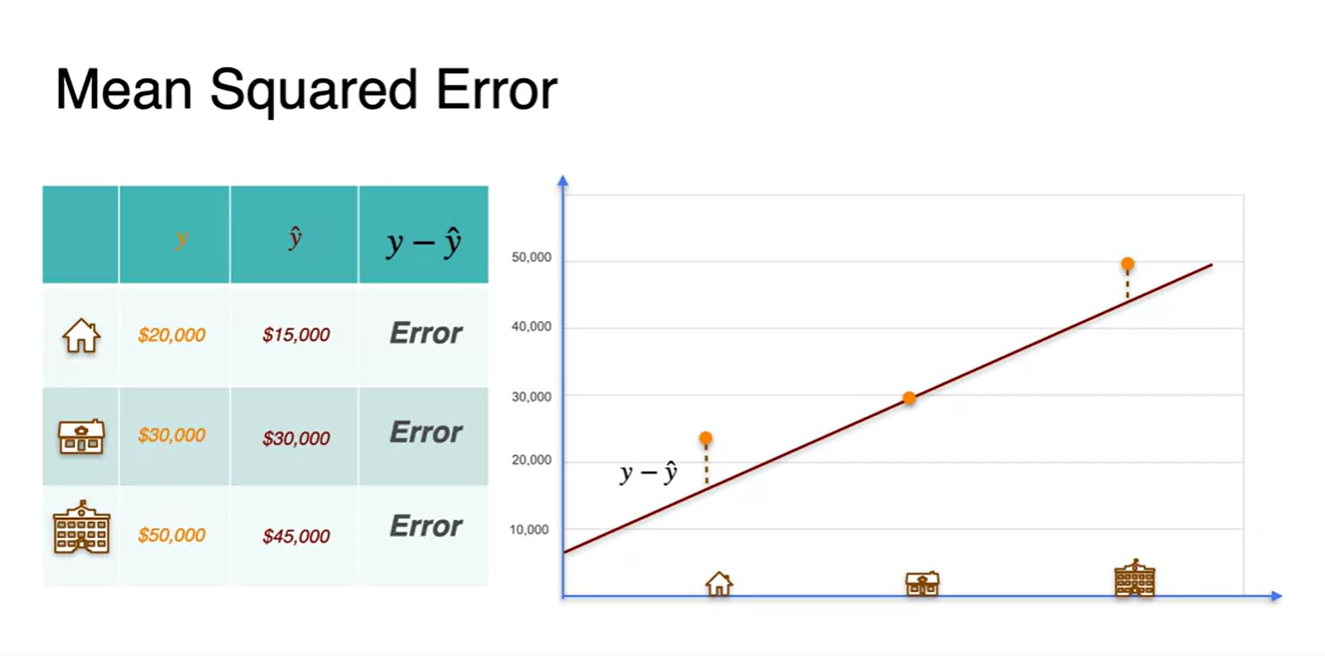
-
그러나 편차의 개념인 제곱과 미분의 용이성을 위하여 최종 Error는 다음과 같이 정의하겠다.
- Error :
-
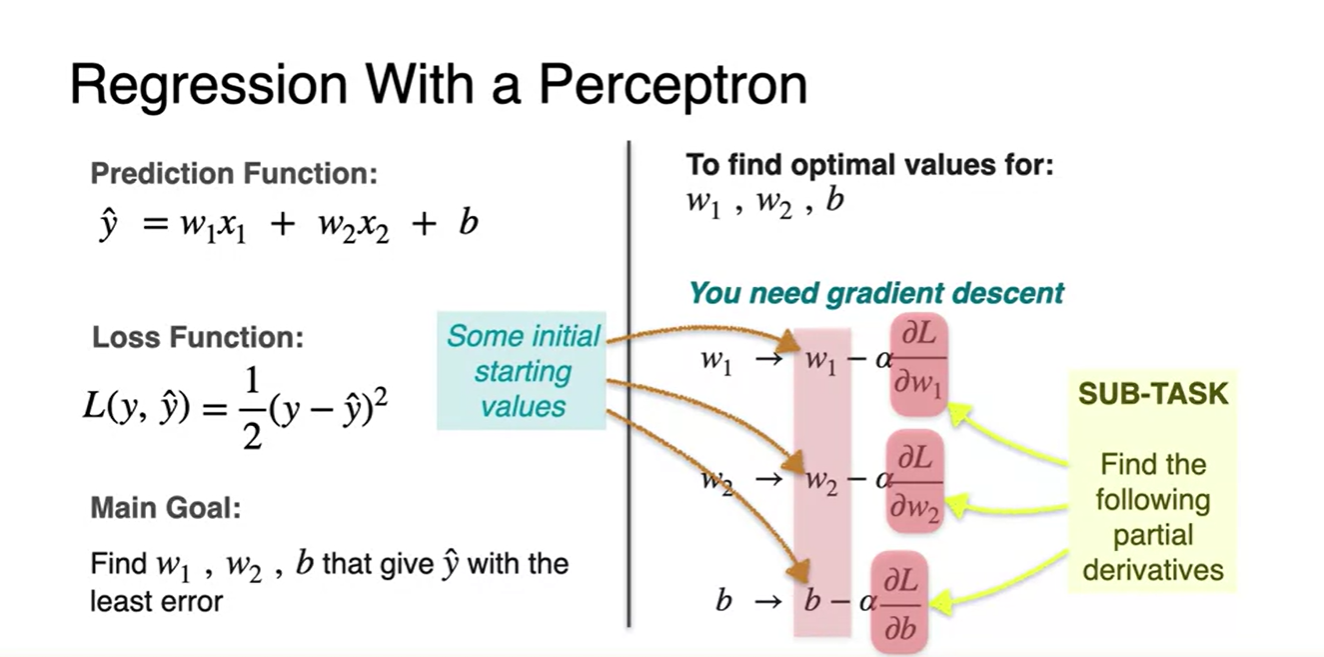
Regression 문제를 단층 Perceptron으로 그리면 아래 그림과 같고
- 최종 Loss function은 으로 정의된다.

Regression with a perceptron - Gradient Descent
-
Predict function과 Loss를 알았으면 이제 해야할 일은 parameter update 과정이다.
-
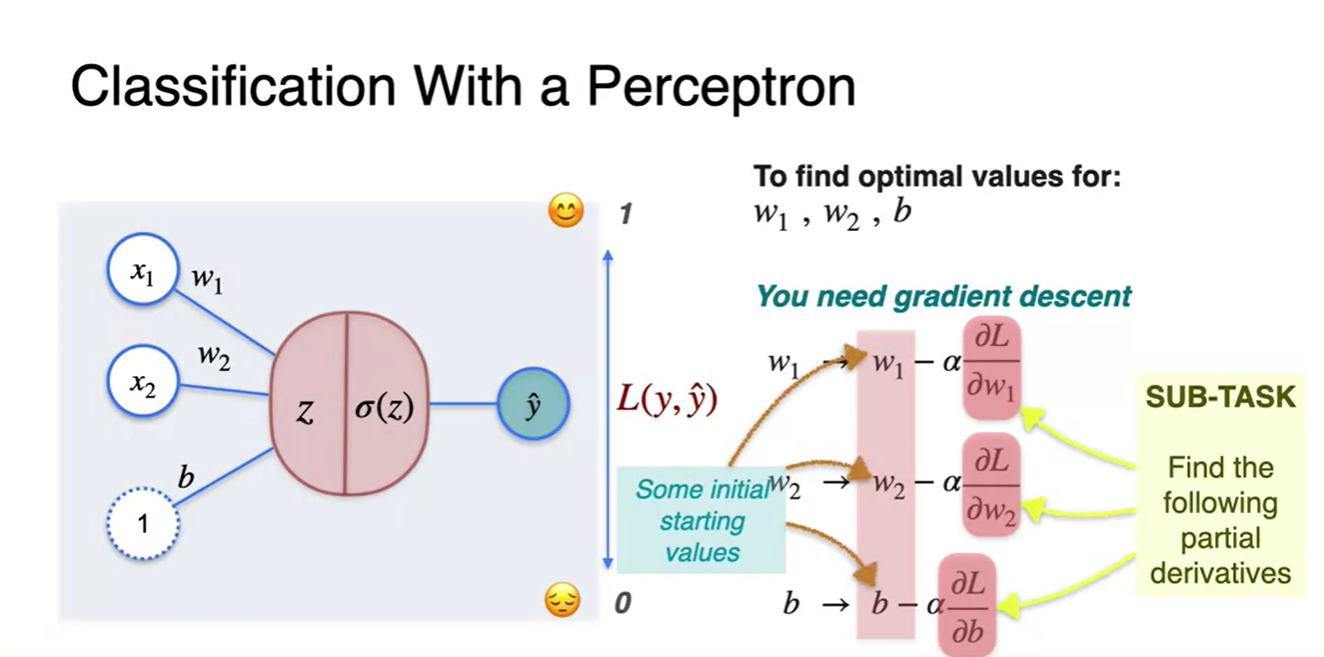
우리가 알아야 할 term은 아래 그림의 진한 분홍으로 색칠되어 있는 부분이다.
-
각 parameter로 Loss를 partial 미분한 값을 말한다.
, ,
-
-
-
Loss에 관한 parameter 편미분은 그 자체로는 쉽지 않다.
-
왜냐하면 나 의 값이 Loss에 직접적으로 정의되어 있지 않고 에 정의되어 있기 때문이다.
-
따라서 우리는 chain rule을 활용하여 미분 자체를 펼쳐줄 것이고, 최종적으로 우리가 찾아야 할 값은 아래 색칠된 4개의 값이다. (중복)
, , ,
-
-

-
아래는 각 변수에 관하여 partial 미분한 결과를 나타낸 표이다.
- 색칠된 곳은 강의 슬라이드에서 보여준 전개 과정이 포함된 것이라 크게 신경쓸 필요 없다.

-
우리가 chain rule을 통해 알아할 모든 값을 찾았다면 원래의 update 값에 대입할 것이다.
- 그 결과, 이미 찾아놓거나 data 값인 , , 만을 대입하여 gradient value를 알아낼 수 있다는 점 또한 시사점이다.

-
그리하여 우리는 아래와 같은 수식으로 gradient descent를 간편하게 행할 수 있다.

Classification with Perceptron
-
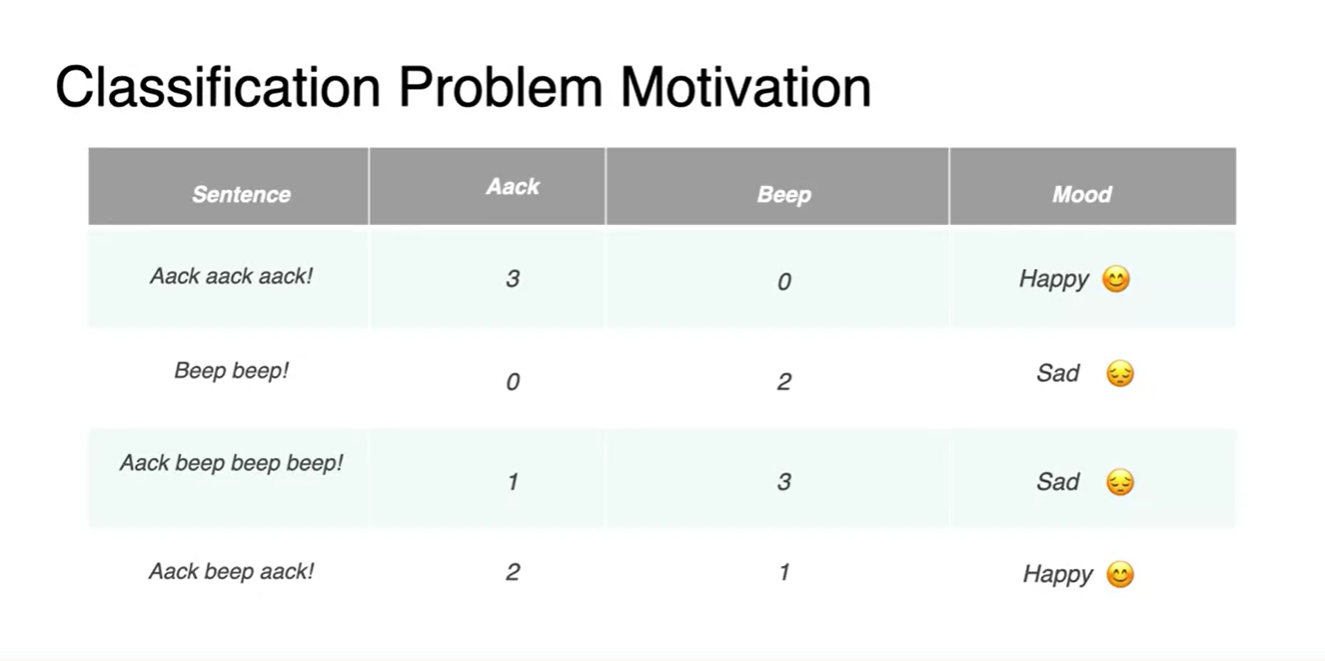
아래와 같은 4가지 특징을 나타내는 데이터 matrix가 존재한다고 해보자.
- 여러 feature들의 연관성을 보고 이 문장의 sentimet가 happy인지 sad인지 구별하는 task를 수행하고 싶다.
-
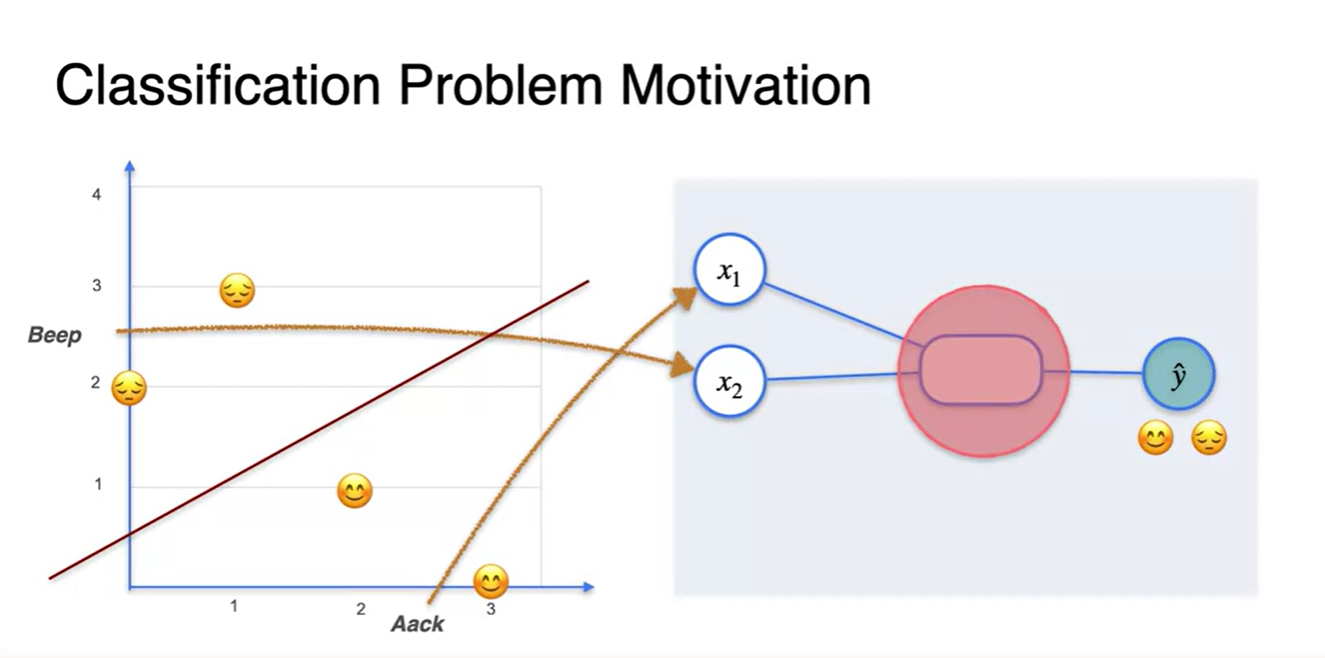
Beep feature와 Aack feature로 축을 그려 data point들을 나타내면 아래쪽이 happy, 위쪽이 sad로 나뉘는 것을 볼 수 있다.
-
우리는 이 두 감정을 구별하는 선형 방정식 직선을 찾아 0과 1로 이진 분류하는 과제를 수행하려는 것이다.
- 이 때 features는 두 변수 concaternated된 [, ] 벡터로 나타낼 수 있고, observative sample m개가 열 기준으로 쌓이면 input dataframe이 된다.
-
-
원소에 각각 곱해지는 가중치 와 bias 까지 더하면
- 수식으로 표현되며 이 값이 바로 예측값 이다.
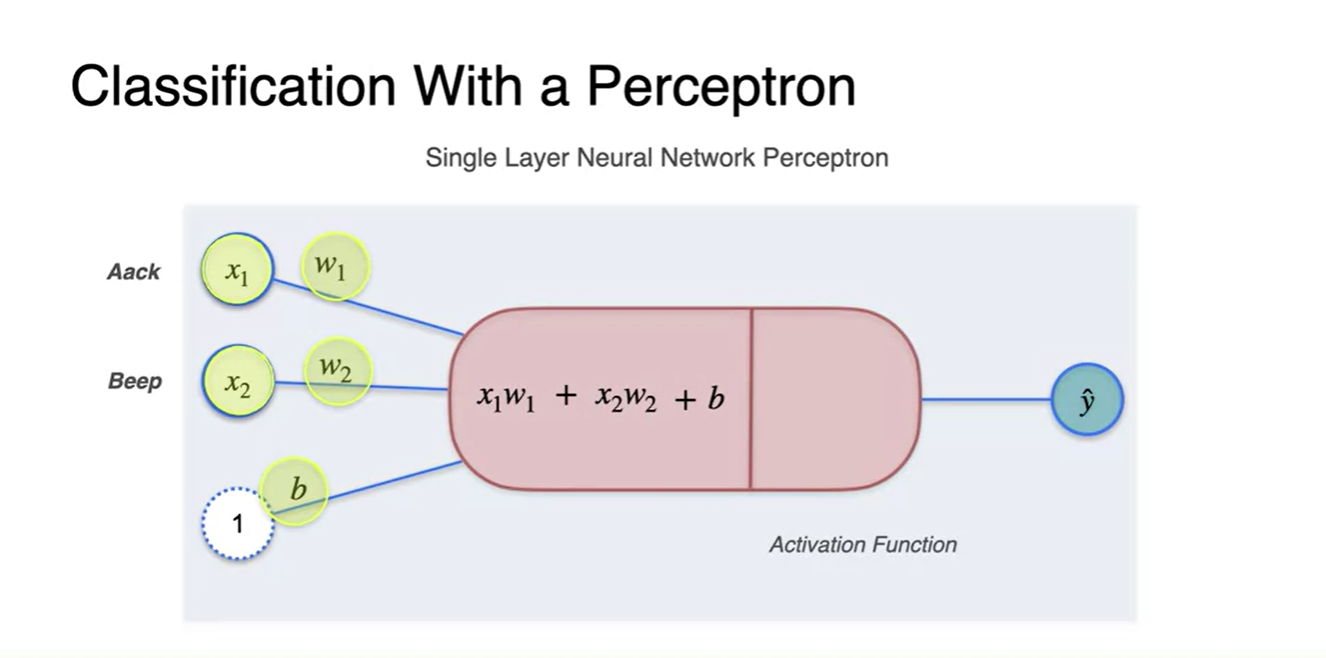
- 이 값은 자연스럽게 continuous한 값일 수밖에 없다는 문제가 있다.
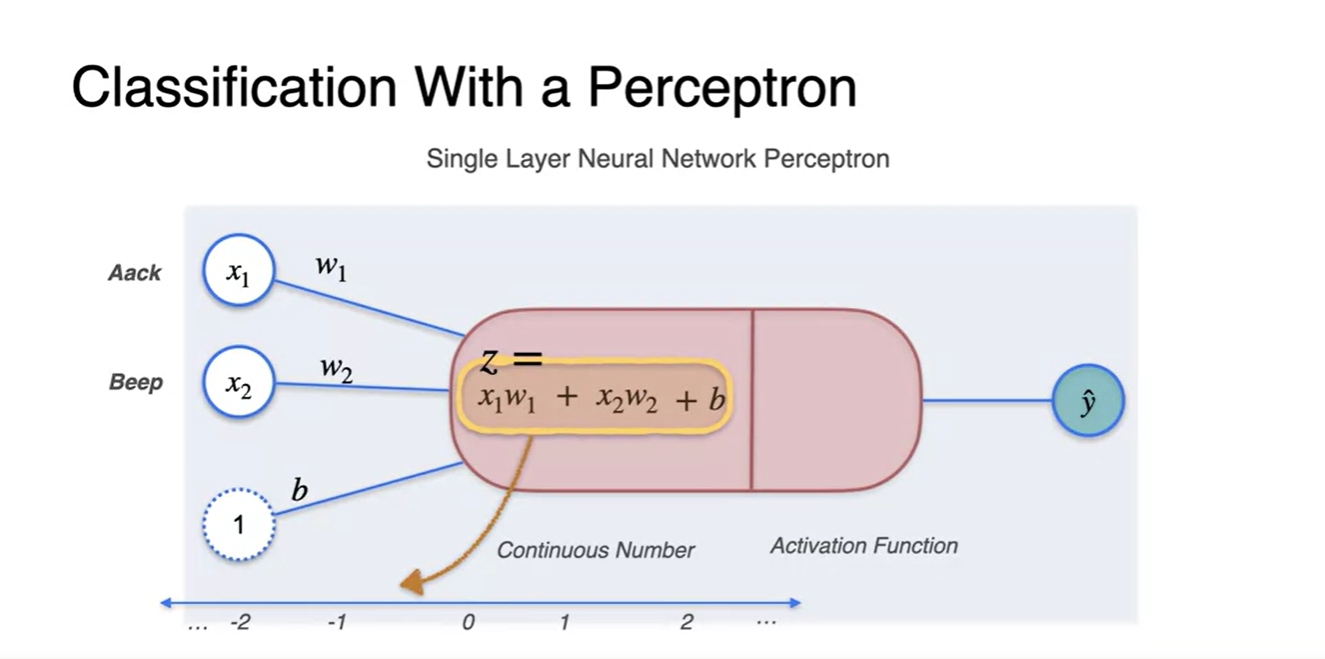
-
우리가 수행하고자 하는 task는 감정을 긍정과 부정 둘로 나누려는 것이기 때문에 0과 1의 값으로 표현된다면 충분히 둘을 구별해낼 수 있다.
- 따라서 activation function인 sigmoid가 그 역할을 해주는 것이며 sigmoid 통과 이후 값은 0과 1 사이의 값으로만 출력되게 된다.
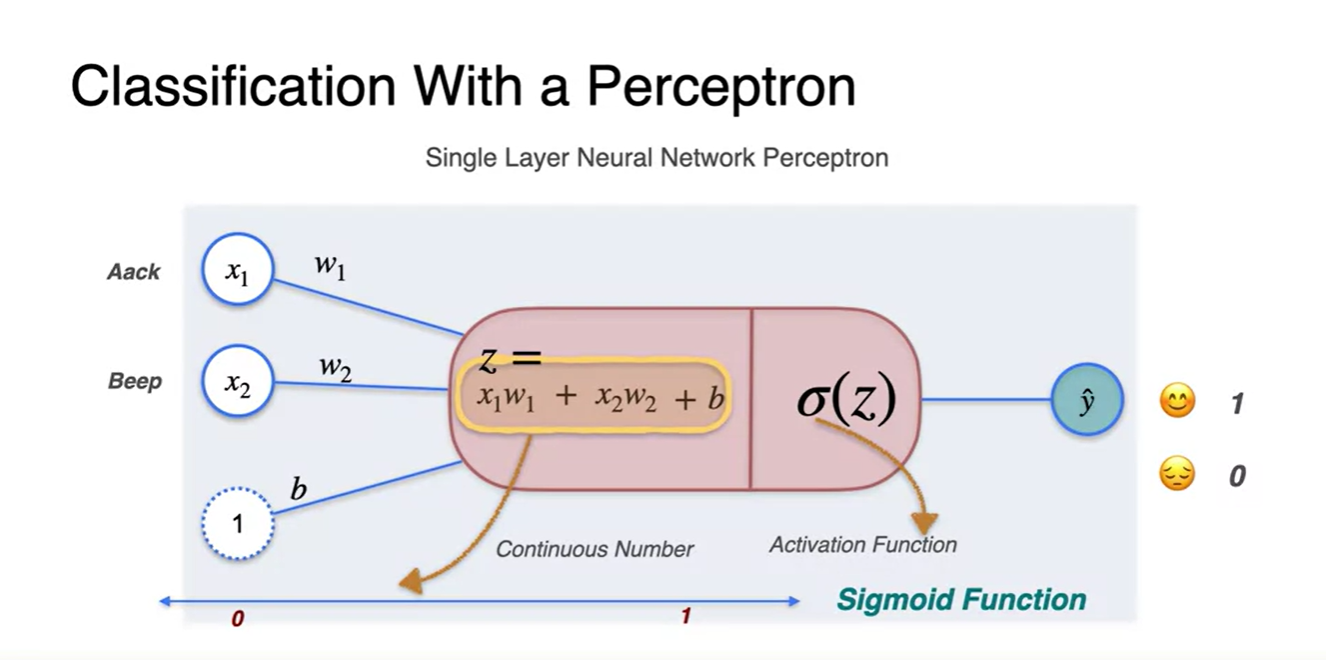
-
Sigmoid 통과 이전의 선형 변환 summation 값을 라고 한다면
-
Sigmoid 함수는 로 나타낼 수 있다.
- 이 값을 0과 1로 출력하게끔 하여 happy와 sad 감정을 분류하게 될 것이다.
-
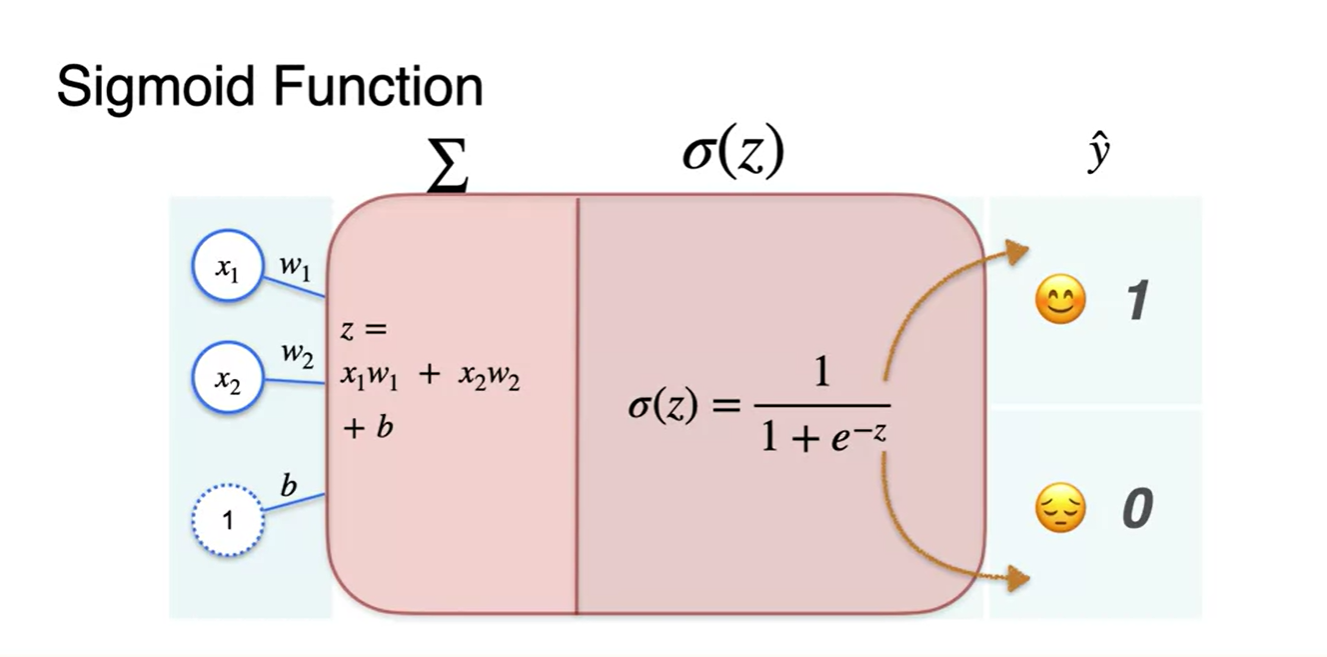
Classification with Perceptron - The sigmoid function
-
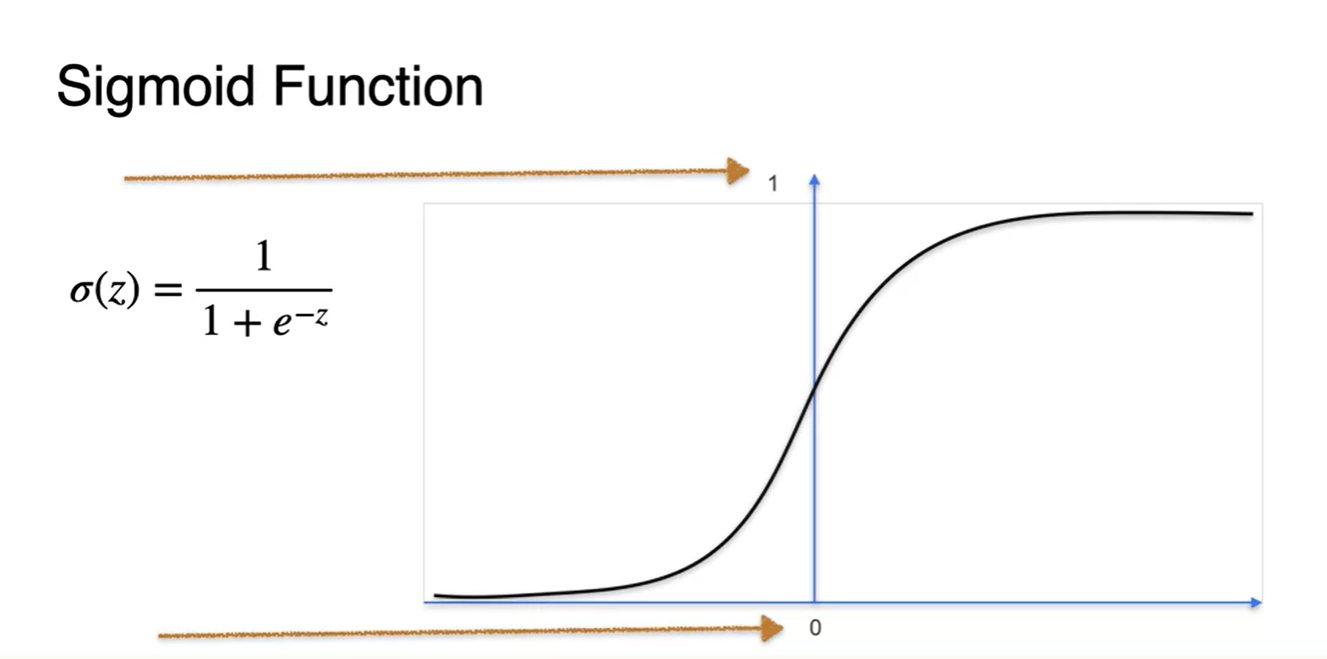
Sigmoid 함수는 0과 1사이의 값을 가지며
- 가 매우 작으면 0에 수렴하고, 가 매우 크면 1로 수렴하는 특징을 갖는다.
-
아래 미분 과정은 (굉장히) 복잡해 보이기 때문에 내 방식대로 미분해보려 한다.
-
[product rule]
-


-
Sigmoid 함수를 미분하면 자기 자신의 값을 Recall 해올 수 있기 때문에
- Backpropagation시 이전 미분 값을 간편하게 넘겨줌으로써 chain rule을 쉽게 적용할 수 있다는 장점이 있다.

Classification with Perceptron - Gradient Descent
-
이제 본격적으로 Perceptron을 활용한 Classification task에서의 Gradient Descent를 적용해보자.
-
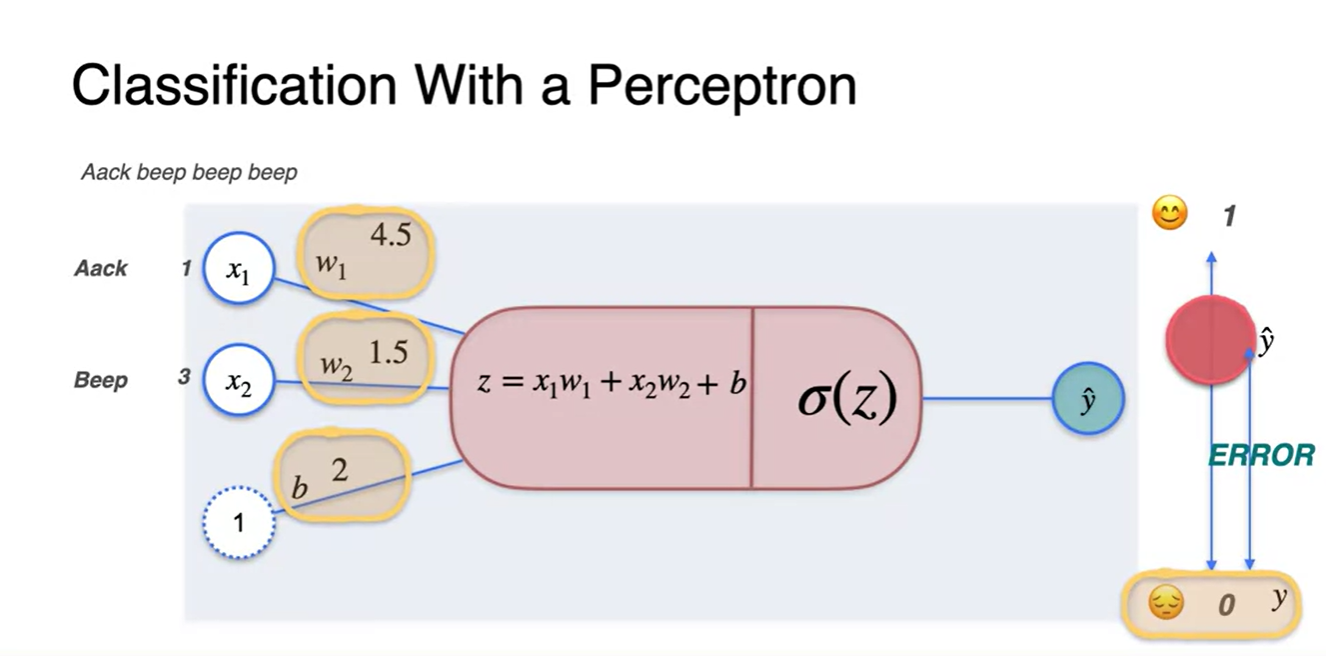
Aack feature와 Beep feature의 값이 각각 1, 3이고 weight value , 가 각각 4.5, 1.5라면 Sigmoid까지 통과시킨 예측값 는 0과 1 사이의 확률값으로 예측될 것이다.
- 만약, 정답이 0으로 표현된 sad라면 추정한 logit과 정답 0의 차이가 Error라는 것을 알 수 있다.
-
-
이 task에서 쓰이는 Loss function은 Log prop 즉, 정답을 최대한 올바르게 추정하고자 하는(전체 확률을 최대화하는) 기댓값을 사용한다.
- MLE 수식으로 나타내면
- Loss로 나타내면

- 우리는 앞으로 새로운 이 Loss를 Gradient Descent하여 parameter를 업데이트하는 과정을 살펴볼 것이다.
Classification with Perceptron - Calculating the derivatives
-
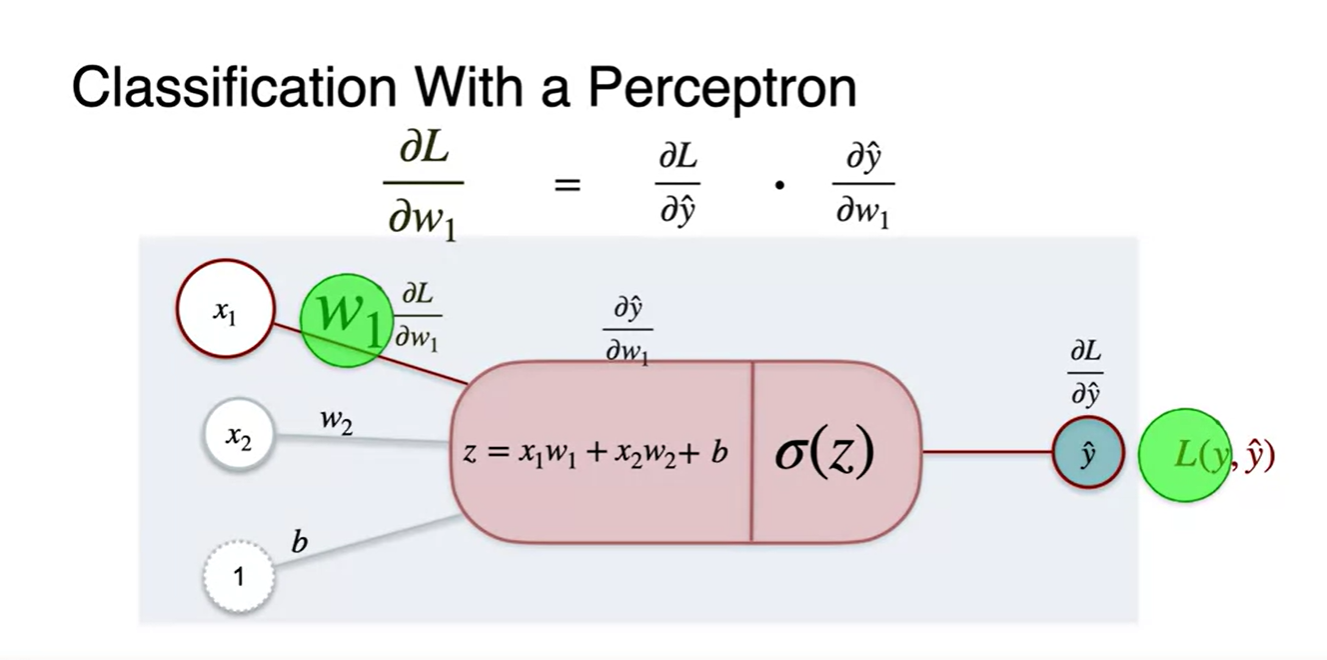
이전에 해왔던 대로, parameter 도함수를 찾기 위해 Loss의 chain rule을 적용하면 아래와 같이 세 변수에 대한 미분으로 전개된다.
-
아직 sigmoid 함수가 적용된 미분을 생략하고 적었다.
-
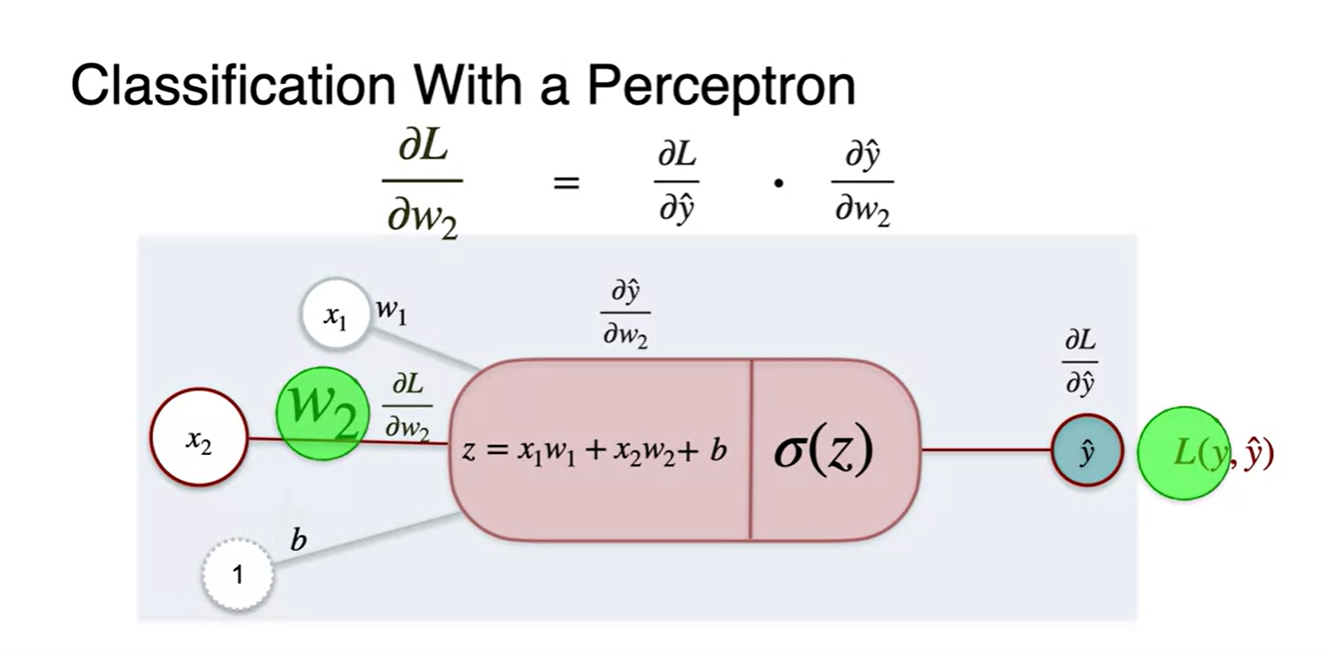
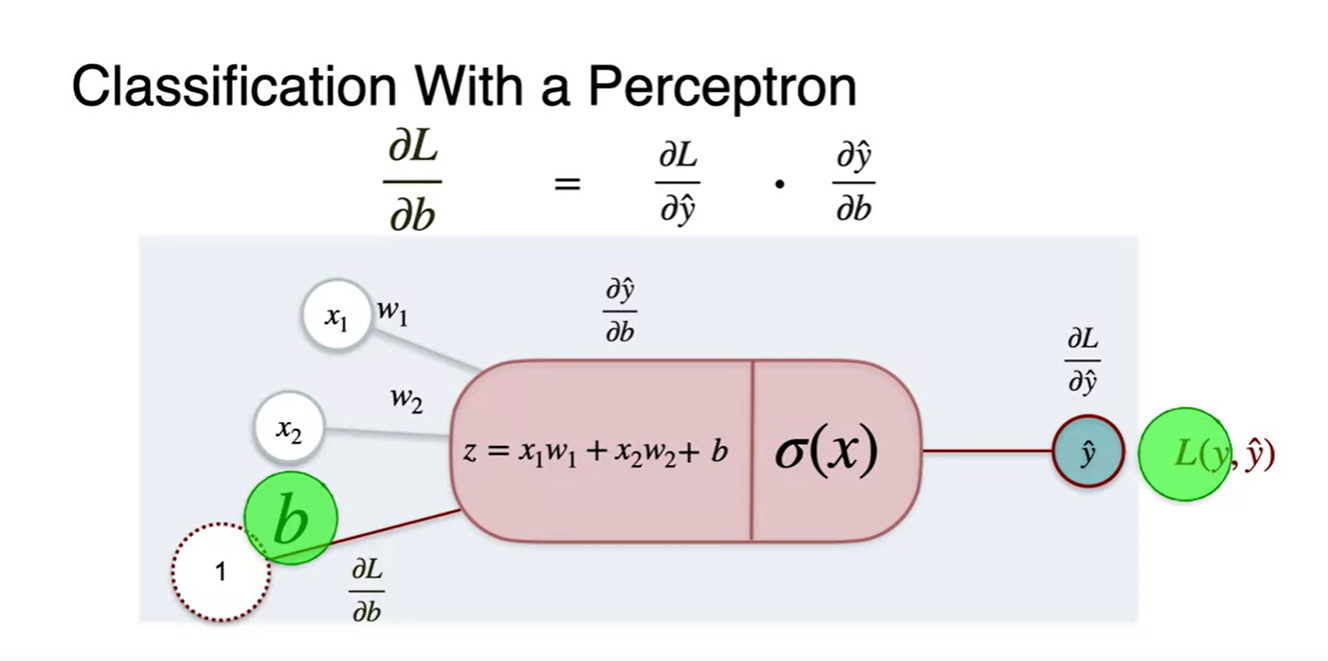
- 새롭게 정의한 Log loss로 gradient descent하는 chain rule은 어떻게 전개할까?

-
먼저 Loss에 대한 의 미분 를 찾아보자.
- 정리하면 이다.

-
아래 식이 전개된 과정은 사실 (*는 , , 중 1)을 전개한 과정으로 보인다.
-
위에서 구한 Sigmoid 함수의 미분까지 적용하여 나타내면 다음과 같이 정리된다.
-

-
Loss에 대한 각 parameter의 미분을 조합해보자.
- 와 (*는 , , 중 1)의 곱으로 전체 Loss 미분을 나타내면 아래와 같다.

- 전개하면 약분 값들이 생기며 이를 삭제해주고 난 최종 function은 두 번째 그림과 같다.


-
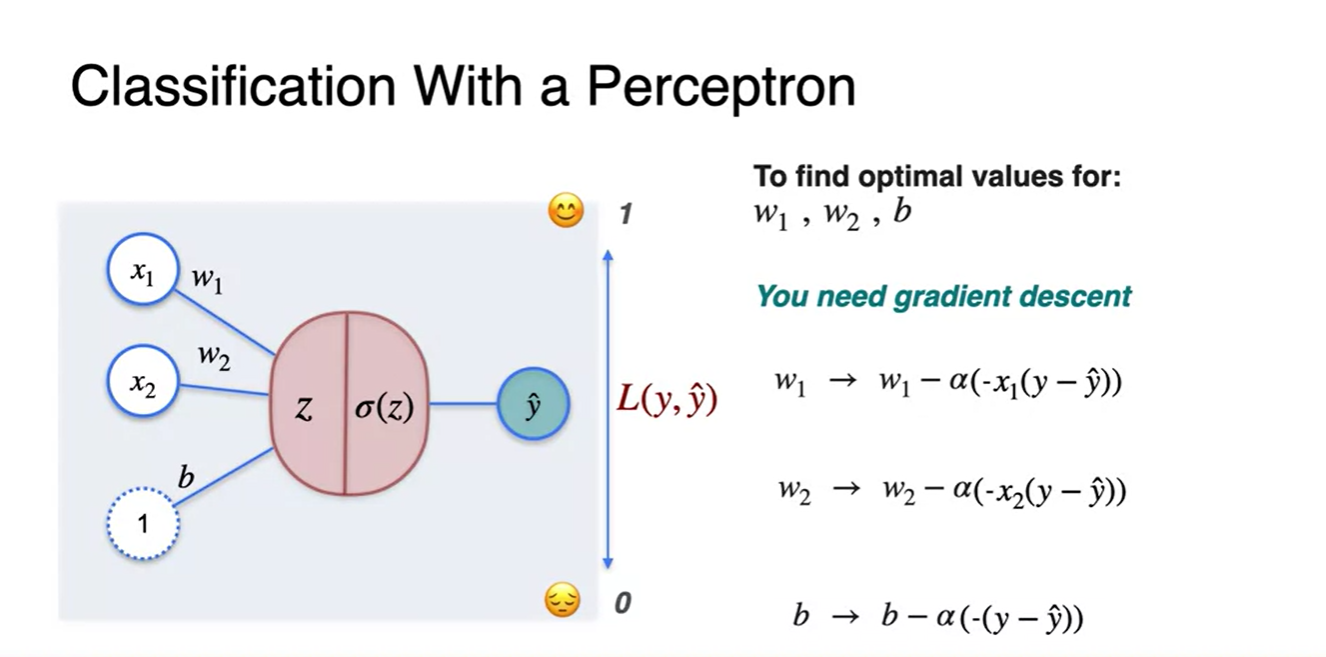
최종적으로 우리는 Classification에 쓰이는 Log loss를 사용하여 gradient descent를 수행하였다.
-
현재는 Sigmoid를 activation function으로 활용했기 때문에 아래와 같은 수식을 그대로 적용해도 된다.
- 다른 함수를 사용한다면 수식이 다시 업데이트 되어야 한다.
-
Classification with a Neural Network
-
위에서 다룬 단층 퍼셉트론 Classification 문제를 다시 한번 떠올려보자.
-
Aack과 Beep의 발현 횟수를 통해 해당 발화의 Mood를 happy와 sad로 구분하는 문제였다.
-
두 특징 벡터에 곱해지는 가중치 와 를 찾아내야 했고, 추론값 을 계산하기 위해서 를 계산해 실제 정답 와 비교했다.
-

-
이번에는 다층 퍼셉트론으로 추론값 을 계산해보자.
-
다시 말해, 여러 선형 변환을 거쳐 더 정밀한 값을 얻어낼 수 있다고 가정하는 것이다.
-
현재는 2 layers 퍼셉트론으로 이루어져 있으며, 구분을 두자면 (input, hidden, output) layer로 나눌 수 있다.
- 여기서 hidden layer가 더 많아진다면 Deep Neural Network라 부르게 된다.
-
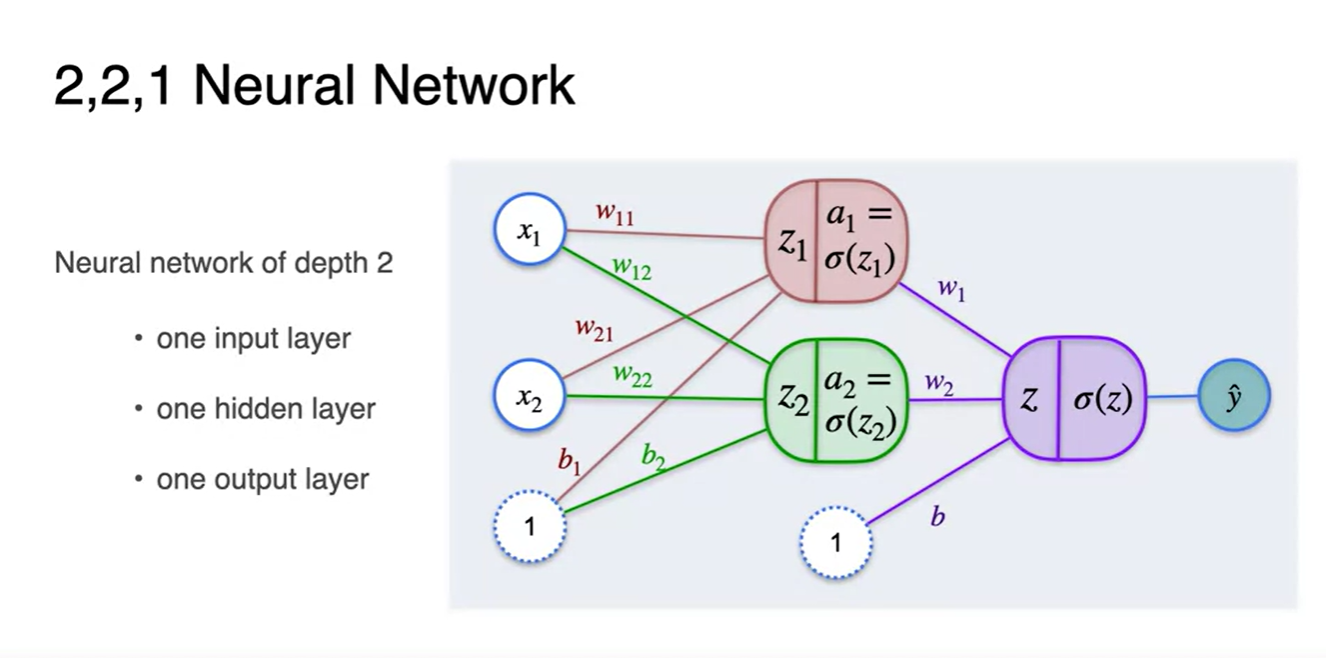
-
수식을 전개해보면 아래와 같다.
-
-
-
- → 아래 Loss에 대입(정답 와 함께)
-
-
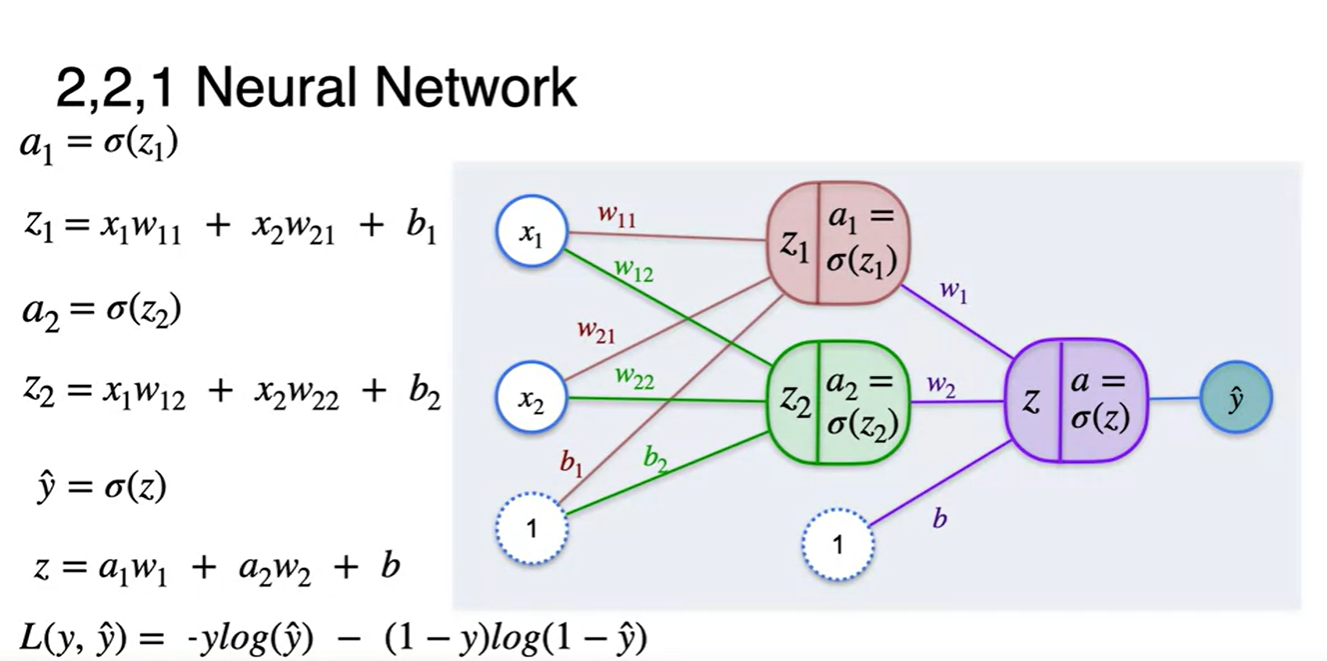
Classification with a Neural Network - Minimizing log-loss
-
우리의 목적은 Loss를 최소화하는 최적의 weights와 biases를 찾는 일이다.
- 정답과의 차이를 줄이기 위해 각 parameter로 미분한 Loss의 미분량을 찾아 업데이트 시켜줘야 한다.
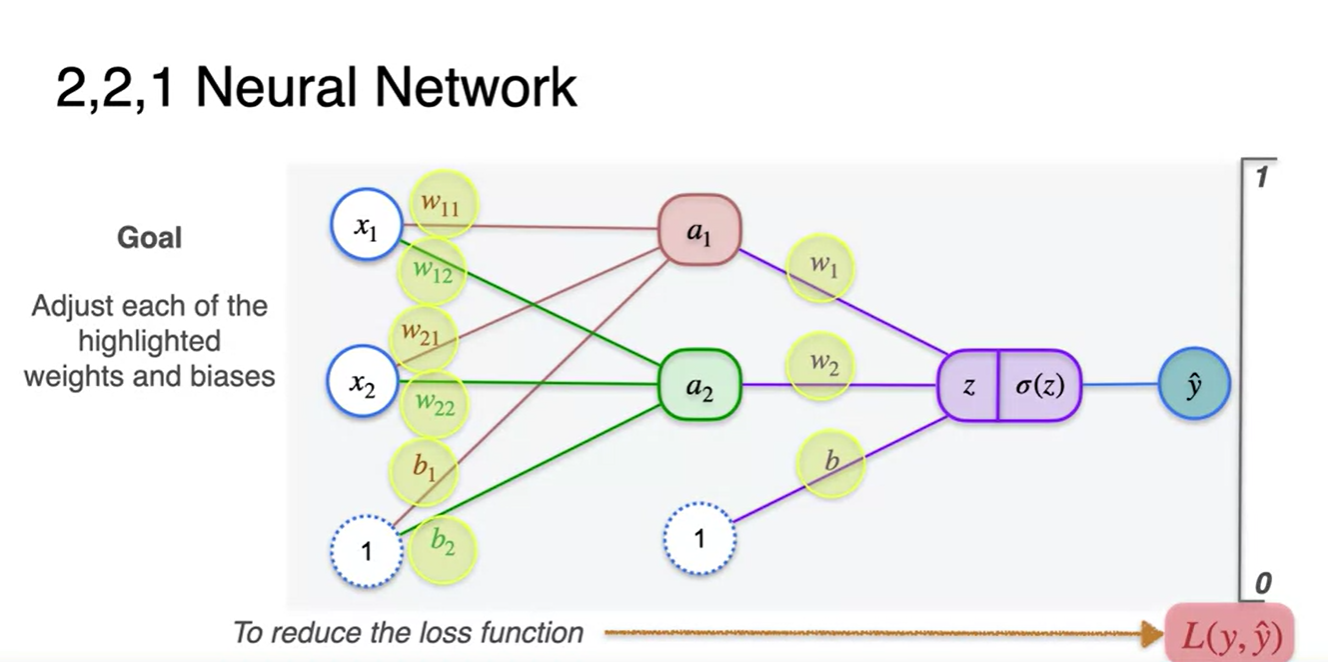
-
각 layer에 적용된 parameter notation으로 표현한 Loss 미분량은 아래와 같다.
-
Input-Hidden layer : ,
-
Hidden-Output layer : ,
-
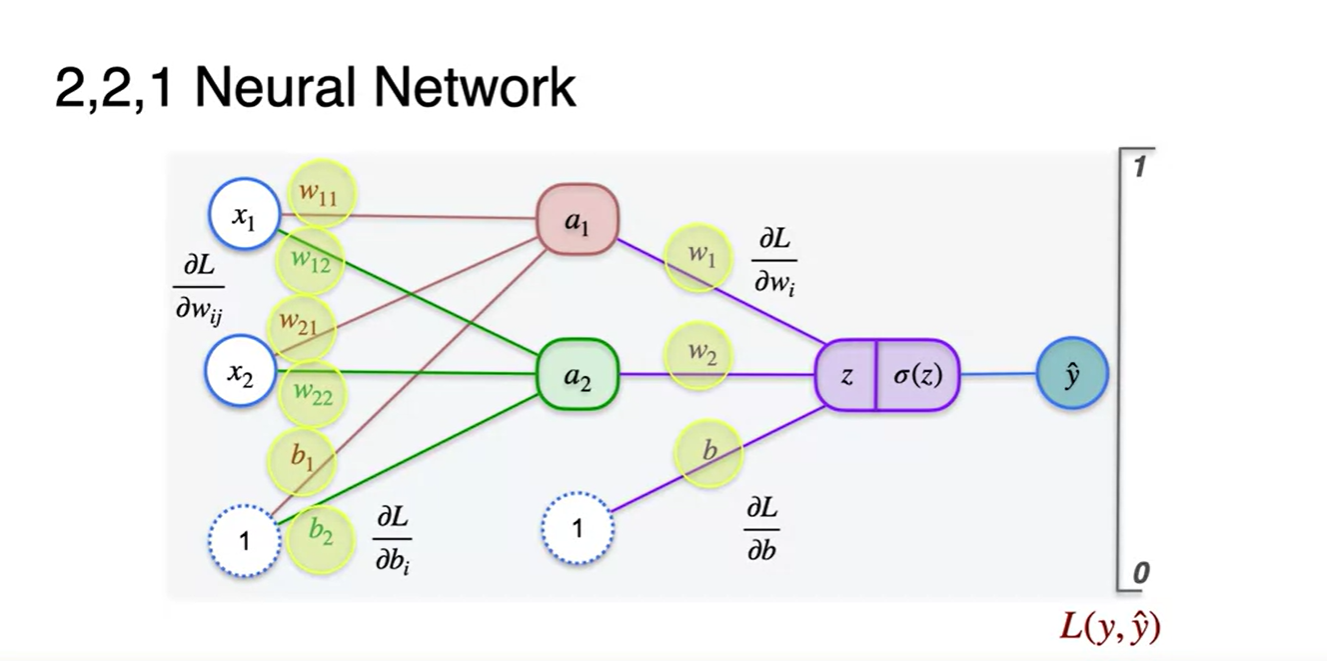
-
단계를 나눠 첫 번째 layer로만 이어지는 Loss 미분량을 연산해보도록 하자.
- 이 때 필요한 값은 , , / , 이다.
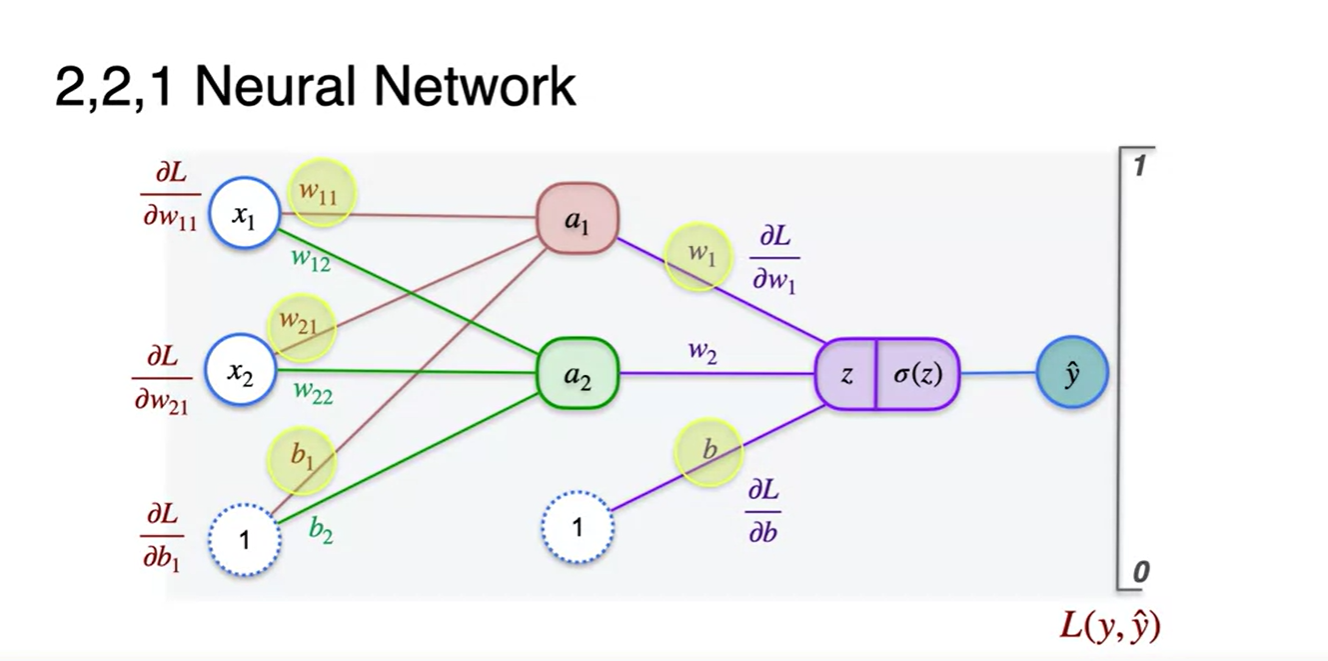
-
내부 계산 과정까지 한 그림에 표현해보면 아래와 같다.
-
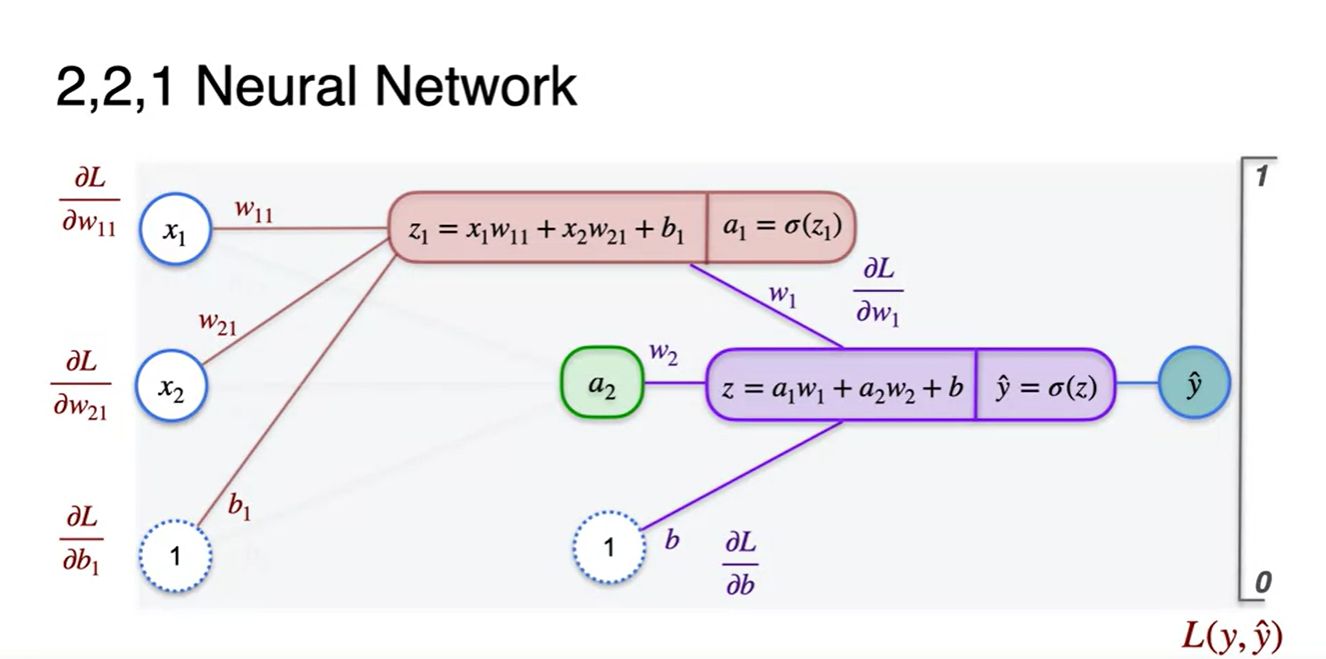
-
parameter로 미분한 Loss 미분량은 어떻게 찾을까?
-
전체 계산 과정으로부터 나온 으로부터 천천히 chain rule을 써가며 정리해보자.
-
오른쪽부터 읽으며 왼쪽으로 향해보라.
-
= * * * *
-
-
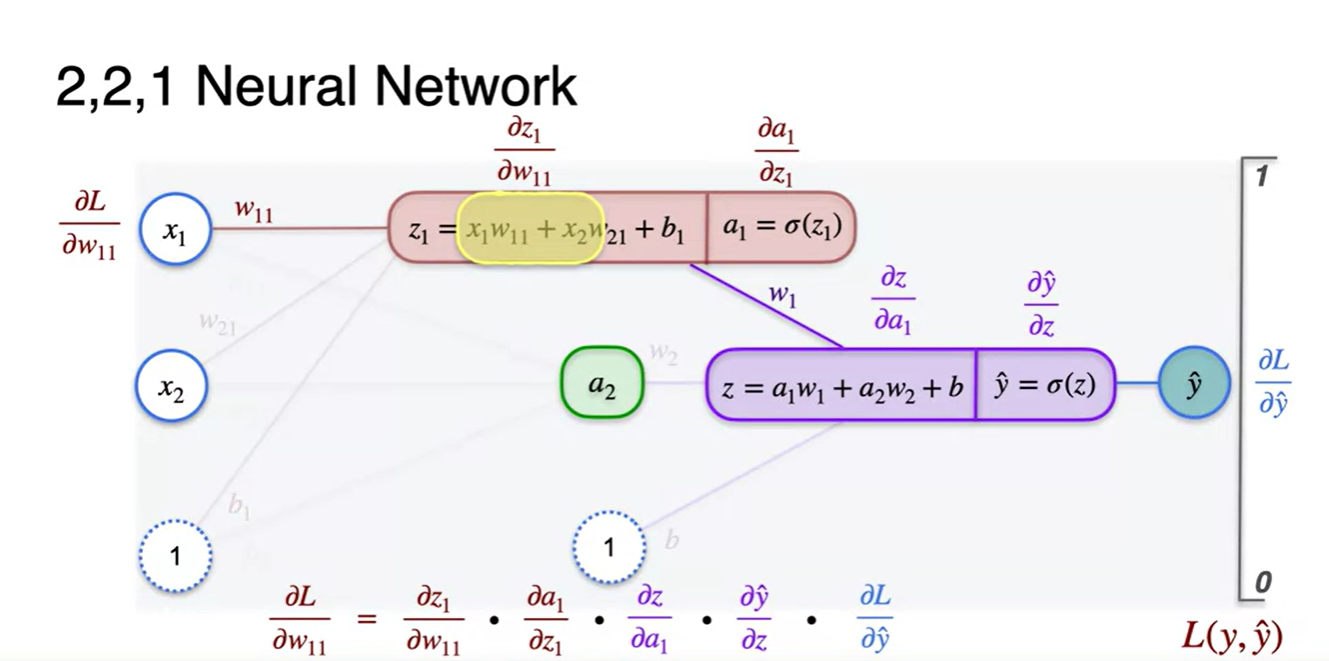
-
위 수식을 차근차근 직접 미분해가며 정리해보자.
-
-
Parameter update :
-

-
이제는 parameter로 미분한 Loss 미분량을 찾아보자.
-
전체 계산 과정으로부터 나온 으로부터 천천히 chain rule을 써가며 정리해보자.
-
오른쪽부터 읽으며 왼쪽으로 향해보라.
-
= * * * *
-
-
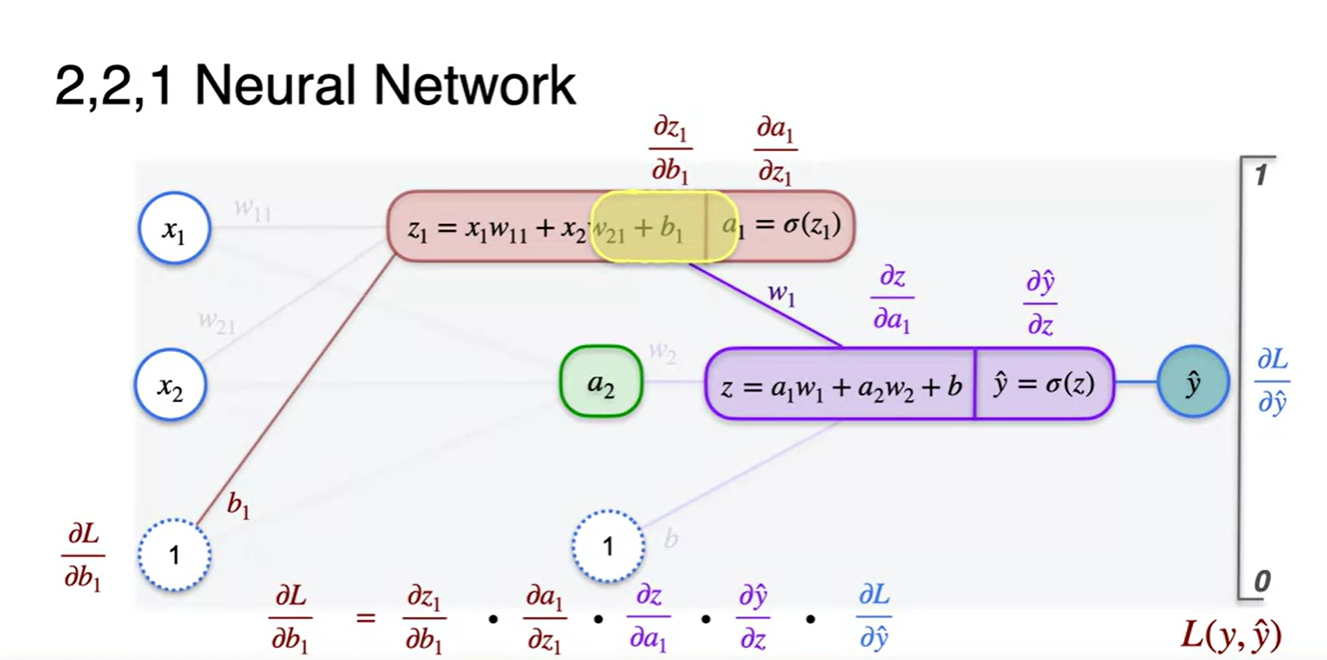
-
위 수식을 차근차근 직접 미분해가며 정리해보자.
-
-
Parameter update :
-

-
전체적인 parameter 업데이트 값을 정리하면 아래와 같다.
-
이 때 주목해보면 좋은 점은 두 번째 layer의 parameter로 들어갈 이 첫 번째 layer의 parameter 업데이트 수식 과정에 포함되어 있다는 점이다.
- 따라서 캐시에 weight값과 출력값을 모두 저장해 back prop시 입맛대로 가져다 쓸 수 있게 만들어야 한다.
-

- 2번째 layer에서의 gradient descent 과정은 단층 퍼셉트론에서 구했던 수식과 완전히 일치한다.
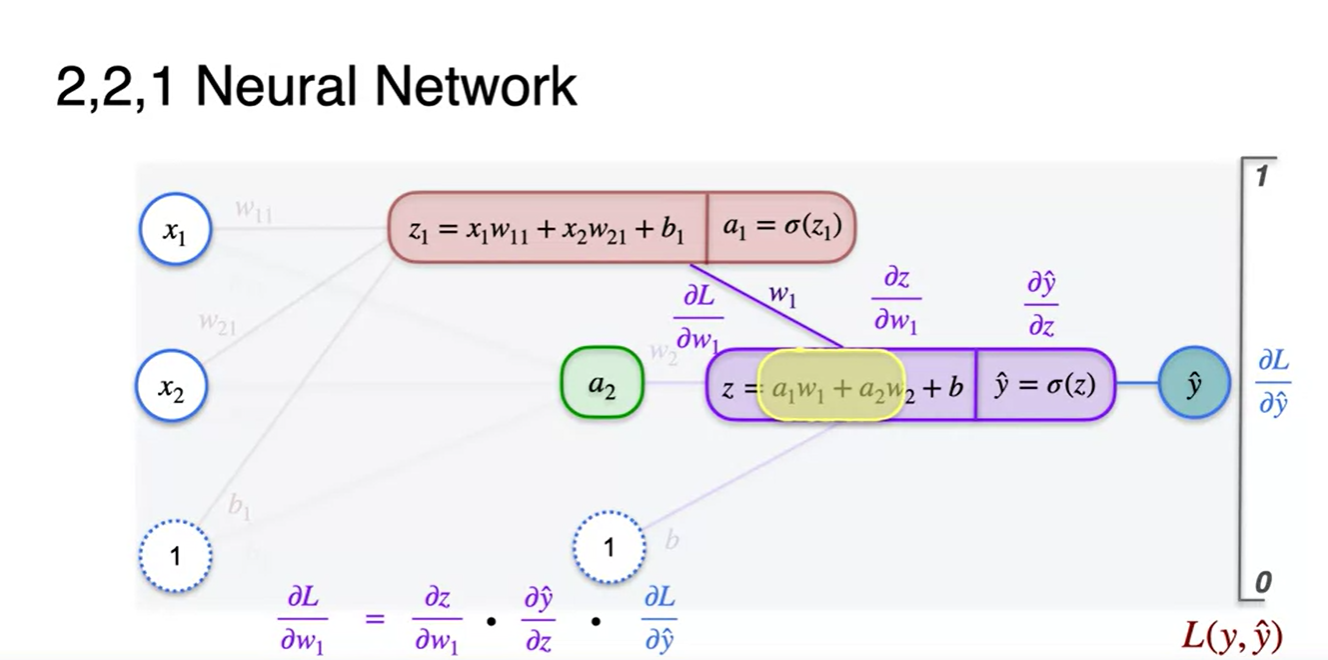
-
그냥 넘어가면 서운하니 전개해보고 넘어가자.
-
= * *
-
Parameter update :
-

- 전체적인 parameter 업데이트 값을 정리하면 아래와 같다.

Gradient Descent and Backpropagation
-
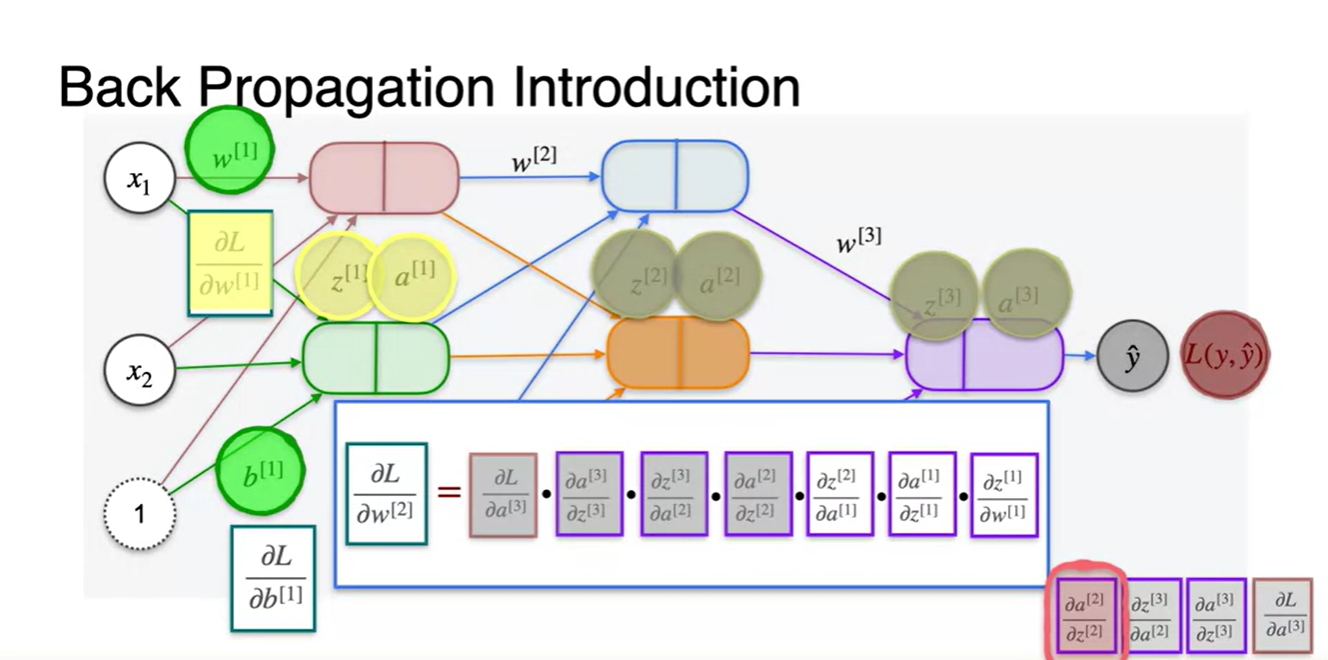
이제 3 layers 다층 퍼셉트론으로 Backpropagation 과정을 반복해보자.
- 각 layer에서 연산되는 변수들의 notation은 오른쪽 위에 이런 식으로 붙어져 표현될 것이다.
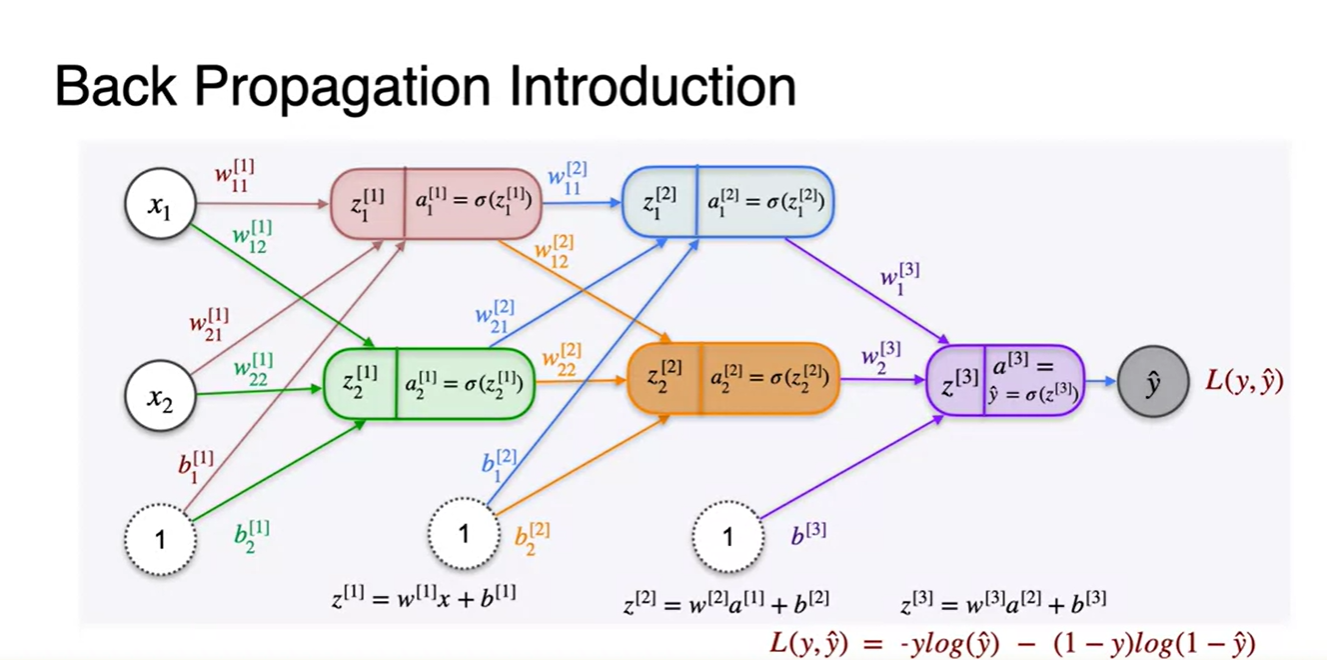
-
모든 layer를 통과하여 나온 추론값 과 정답 를 비교한 Loss를 계산하는 과정까지가 Forward pass 과정이다.
- Backpropagation은 와 parameter로 미분한 Loss 미분량을 찾아내 Loss를 최소화하기 위한 parameter를 각각 update 해내는 과정이다.
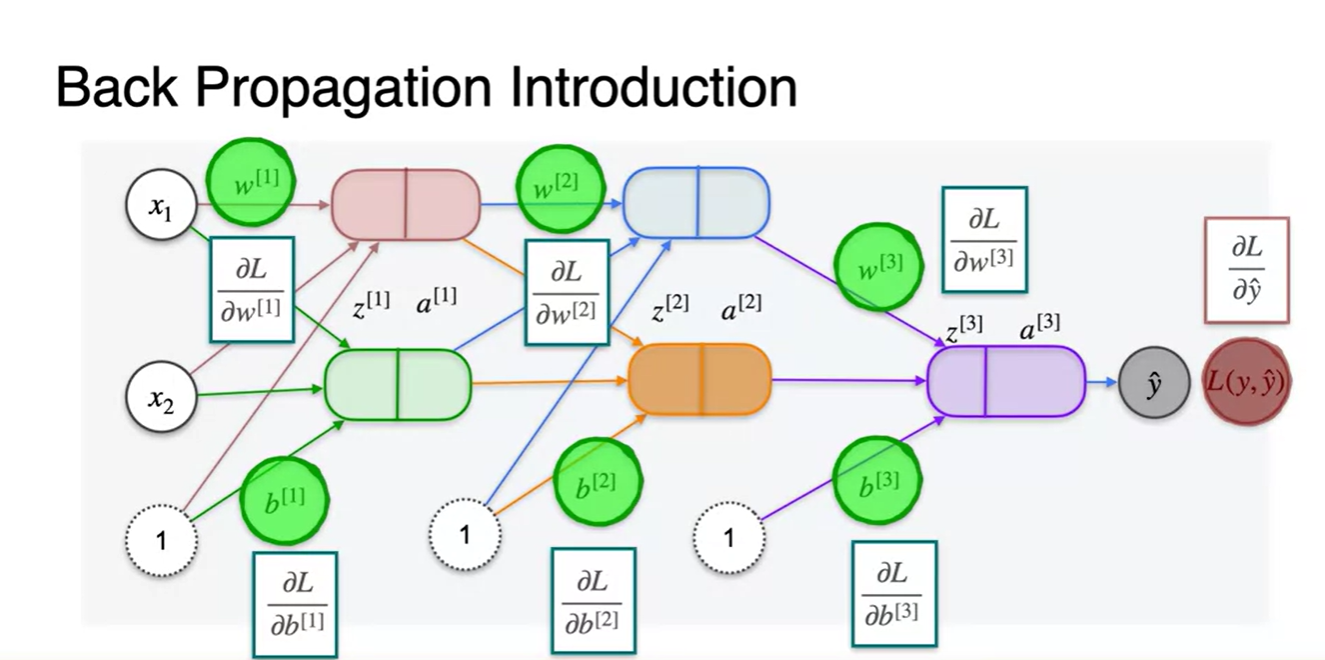
-
가장 마지막 3번 layer에서의 연산 과정을 살펴보자.
-
과 로 미분한 Loss 미분량은 아래의 chain rule을 거쳐 구해진다.
-
=
-
=
-
-
이 과정에서 뒤의 두 항 와 는 중복되기 때문에 cache에 저장해 놓고 이후에 사용할 수 있다.
-
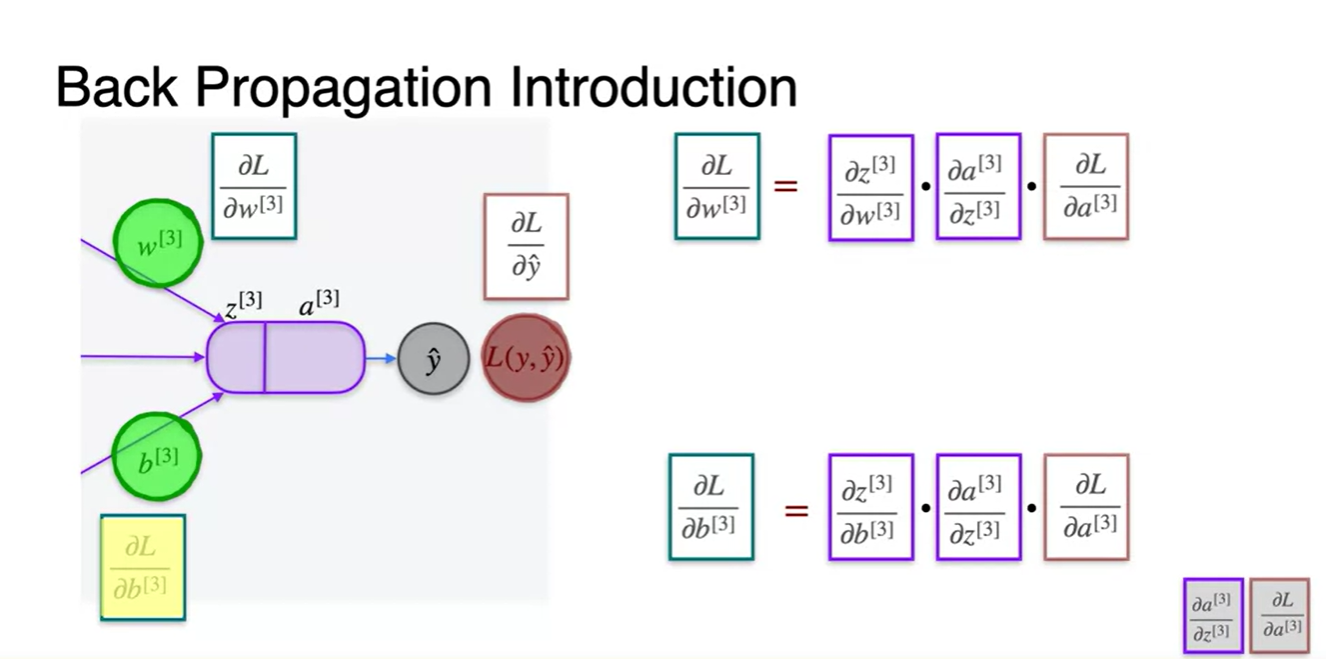
-
2번 & 3번 layer에서의 연산 과정을 살펴보자.
-
과 로 미분한 Loss 미분량은 아래의 chain rule을 거쳐 구해진다.
-
=
-
=
-
-
앞서 계산해 놓은 와 항을 대입하고 새롭게 구한 와 두 항을 cache에 저장해 둔다.
-
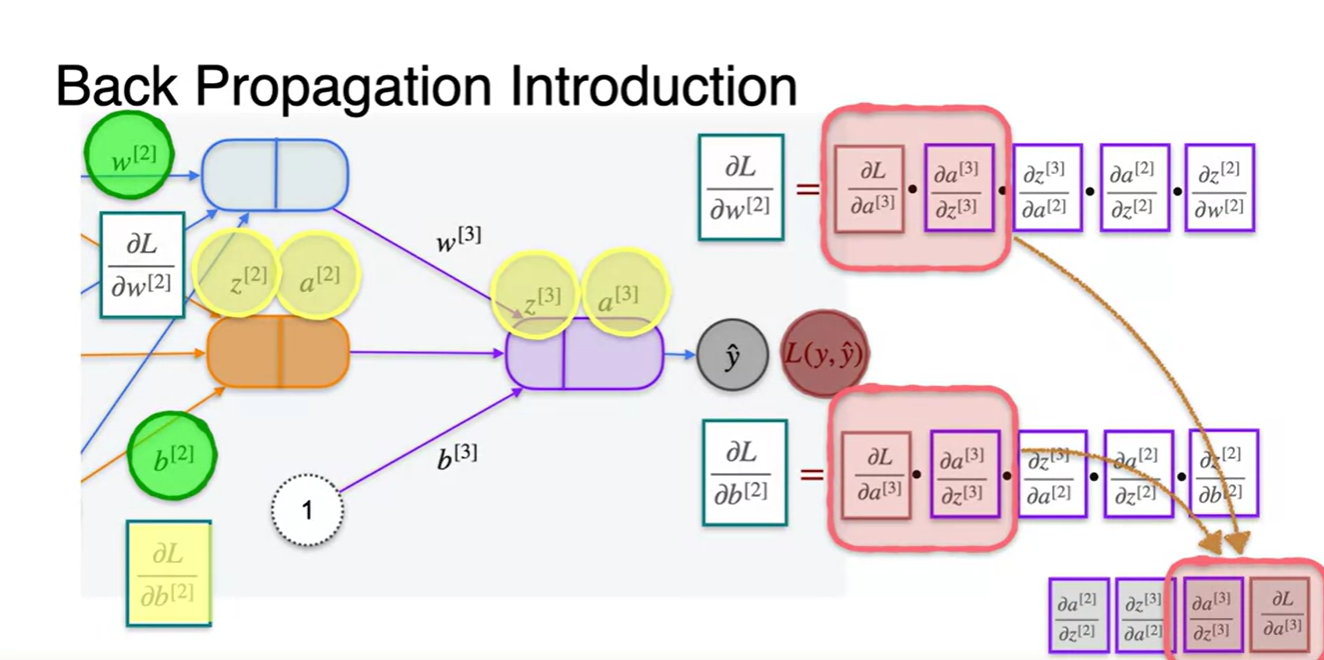
-
마지막으로 1번 layer에서의 연산 과정을 살펴보자.
-
과 로 미분한 Loss 미분량은 아래의 chain rule을 거쳐 구해진다.
-
=
-
=
-
-
앞서 계산해 놓은 , , , 항을 대입하고 나머지 항들을 계산해 parameter 업데이트를 진행한다.
- 그림에서 표현된 → 로 고쳐 읽자. (강사의 오타다.)
-
Lesson 2 - Newton's Method
Newton's Method
-
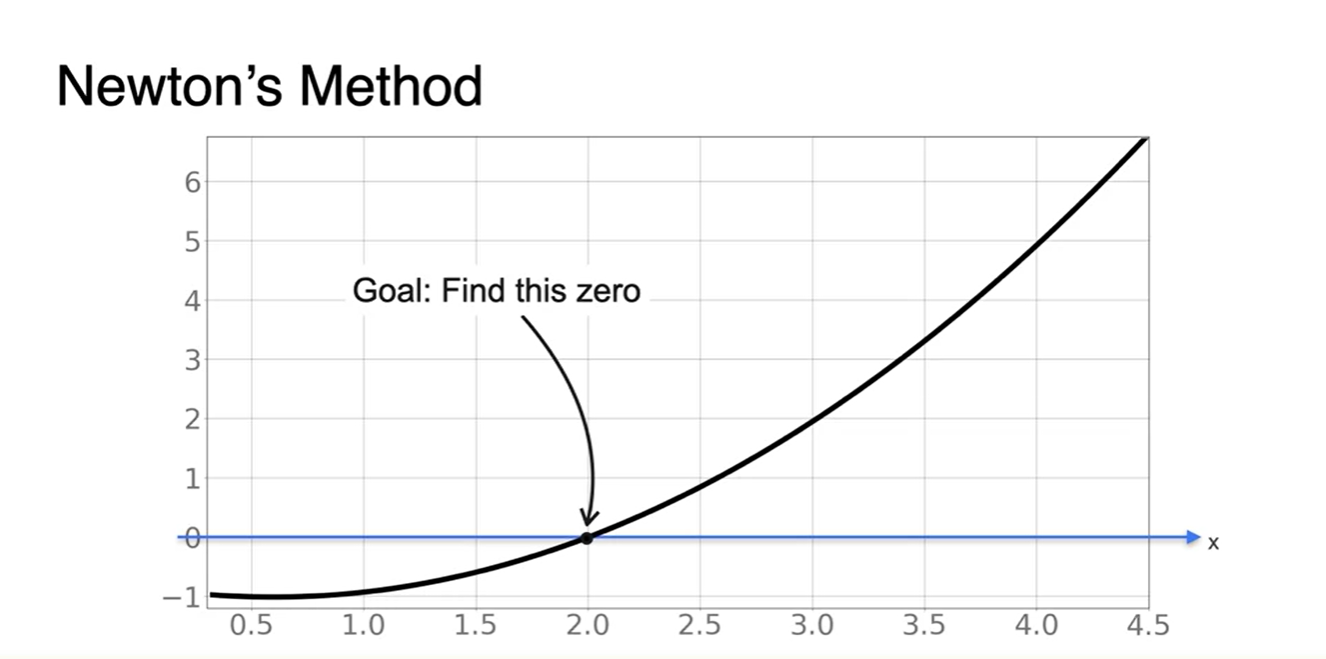
Newton's Method를 활용한 optimizing 기법에 대해 알아보자.
- 우리의 목표는 Loss function의 derivative가 0이 되는 parameter x를 찾는 과정임을 잊지 말자.
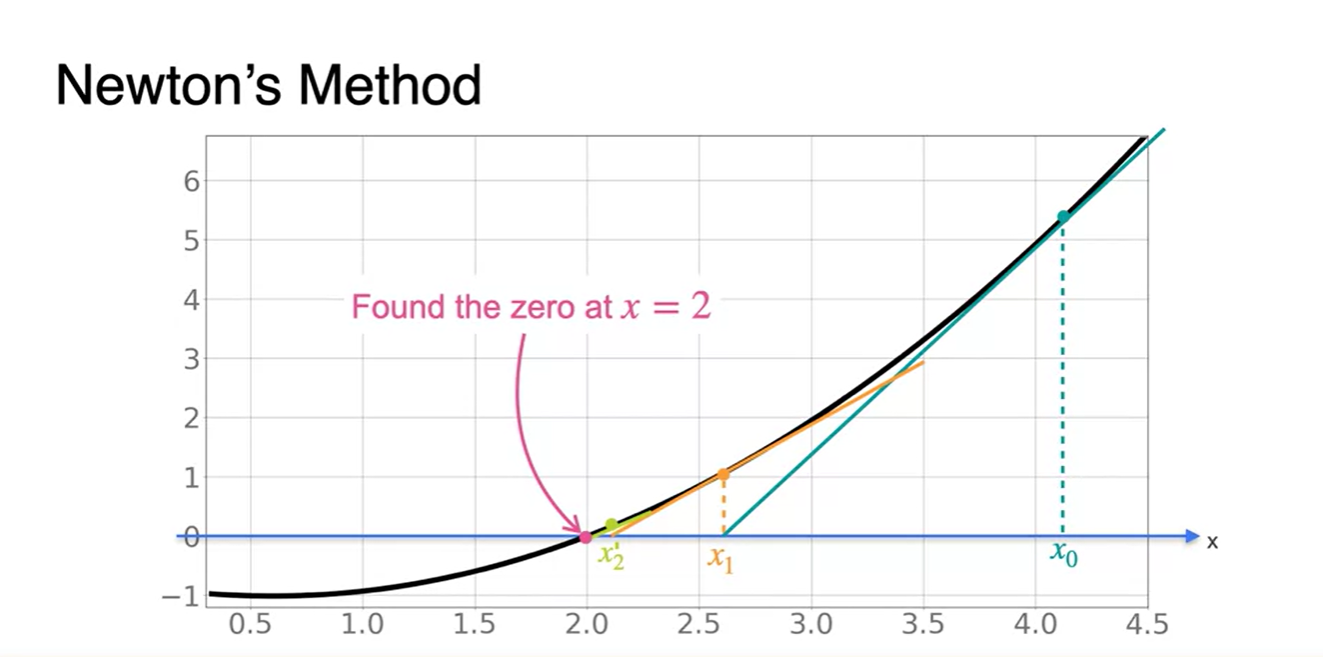
-
초기 지점 에서부터 slope를 구하고, x절편을 찾으면 이 구해진다.
- 의 slope를 통해 다시 x절편을 찾고, 의 slope로 또 다시 x절편을 찾아나가다 보면 해당 function의 value가 0이 되는 x값에 점점 가까워져감을 알 수 있다.
-
지점에서의 미분값으로부터 function을 0으로 만드는 기울기 함수의 x절편 을 찾는 수식을 정리해보자.
-
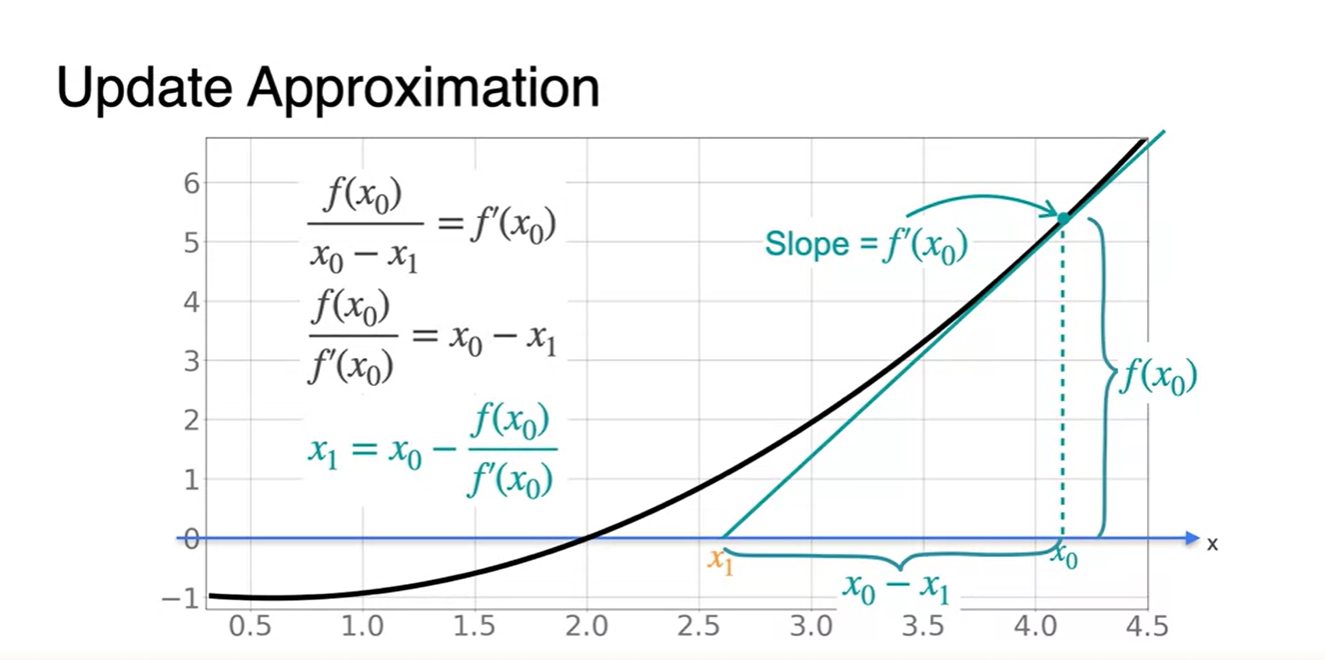
-
일반화된 점화식으로 표현하면 다음과 같다.
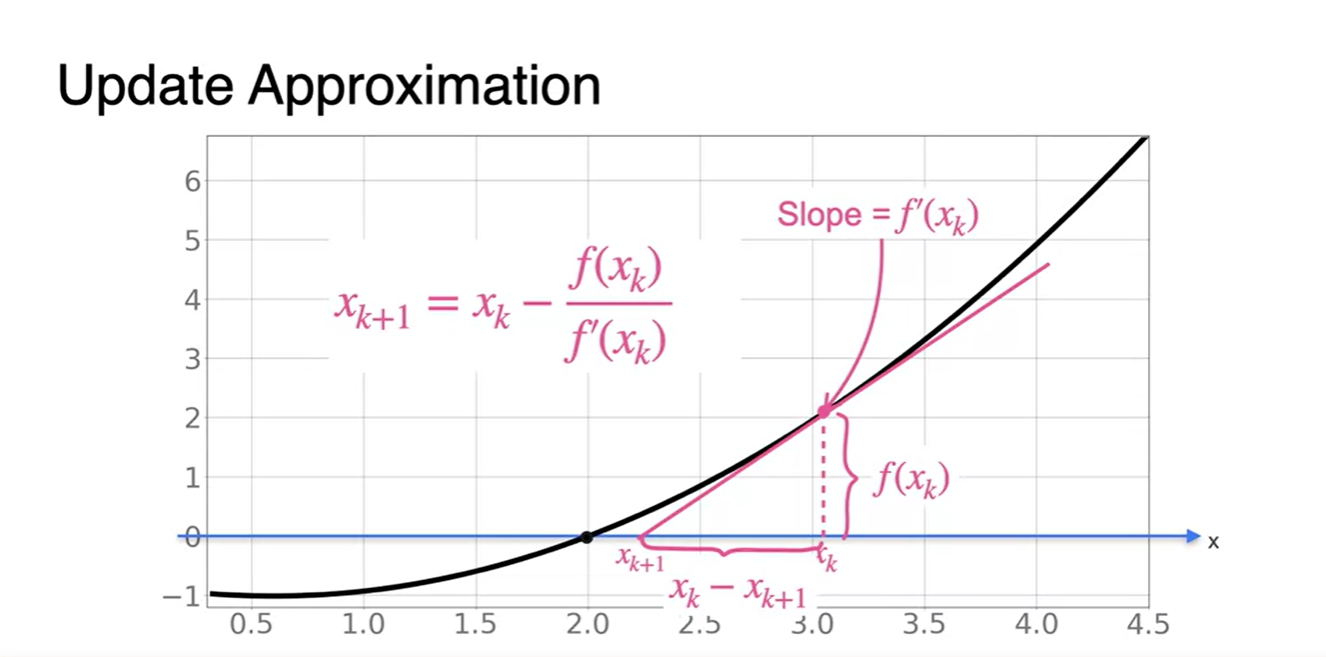
-
그렇다면 이러한 방법론을 어떻게 optimizing에 활용한다는 것일까?
-
Newton's method는 를 0으로 만드는 x값을 찾아나가는 수식이다.
- 이러한 맥락에서 Loss function의 derivative 함수를 0으로 만드는 것과 동일한 기법이라 볼 수 있다.
-
Newton's method의 는 Loss function 의 미분 함수 다.
-
우리는 를 0으로 만족시키는 parameter x값을 구하기 위해 의 미분 도함수 즉, 이계도함수가 추가로 필요하다.
-

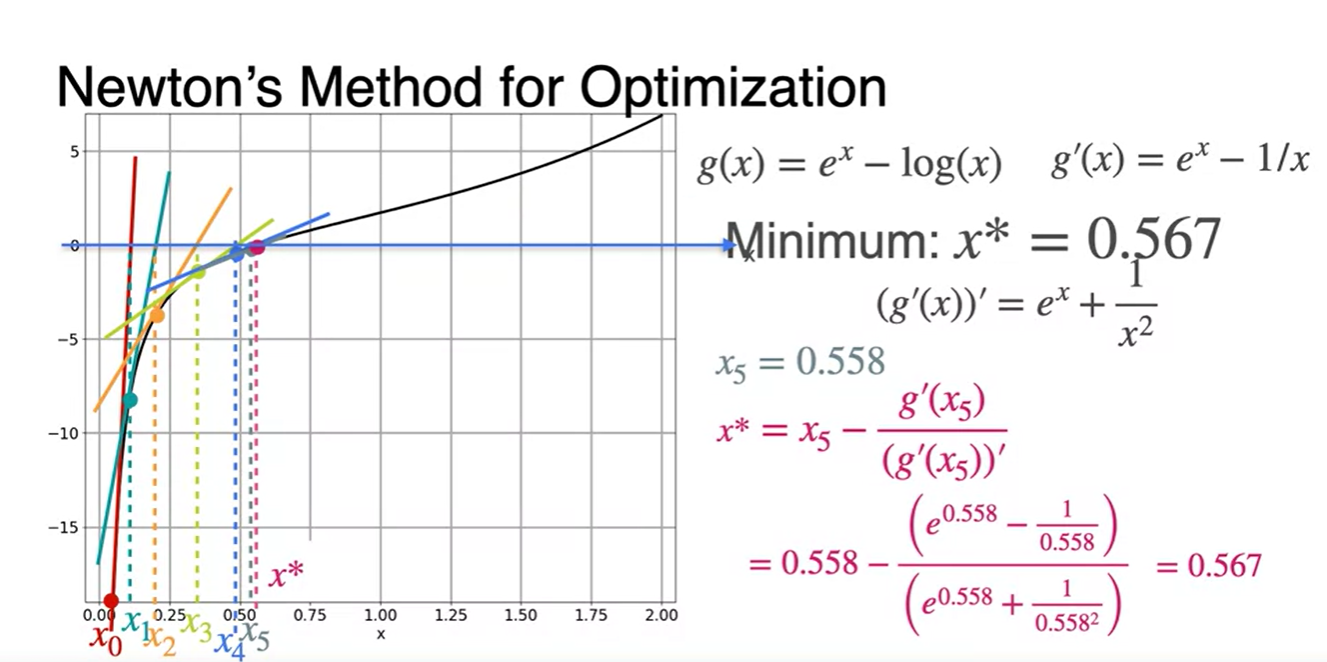
Newton's Method: An example
-
기존 함수를 알 때, 이 함수를 minimize하는 parameter x값은 인 지점에서의 x값을 찾으면 다.
- 원래 함수는 이며, 다.
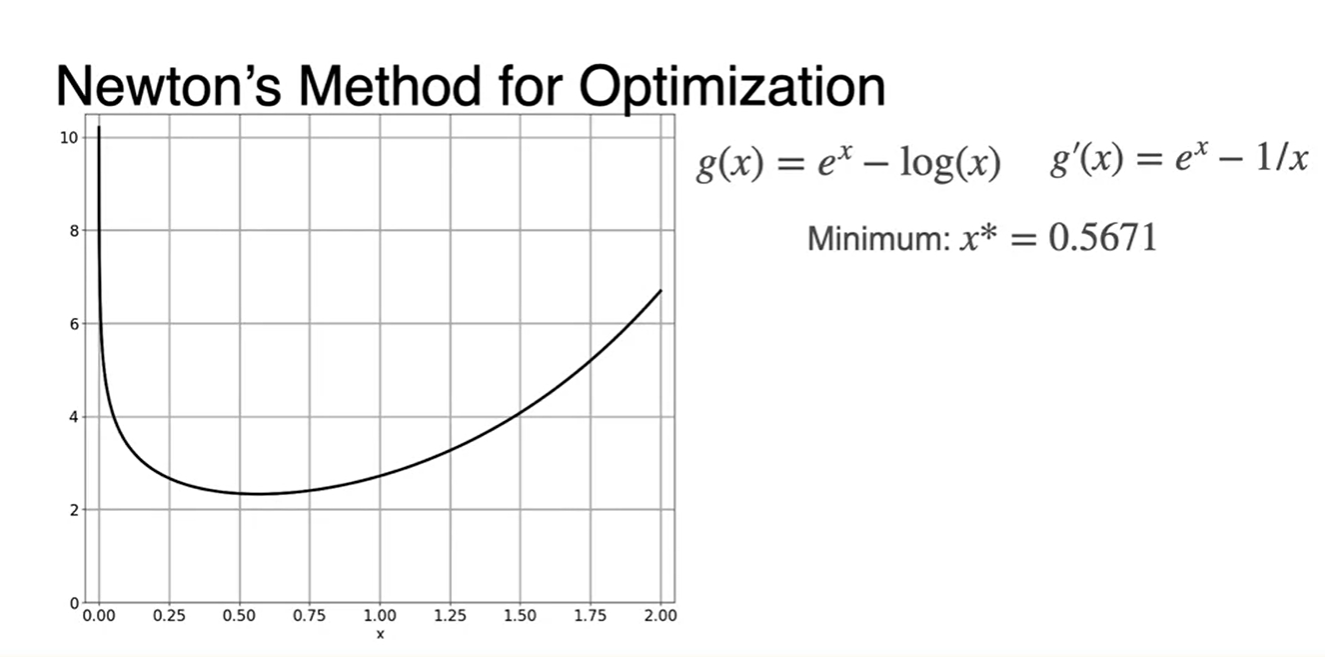
-
다시 말해, 아래 새롭게 그려진 함수가 0이 되는 x값을 찾는 것이 핵심이라는 것이다.
-
이는 위에서 말한 Newton's method를 통해 이계도함수 를 구하여 추정하는 방법으로도 가능하다.
-
함수의 이계도함수 이다.
-
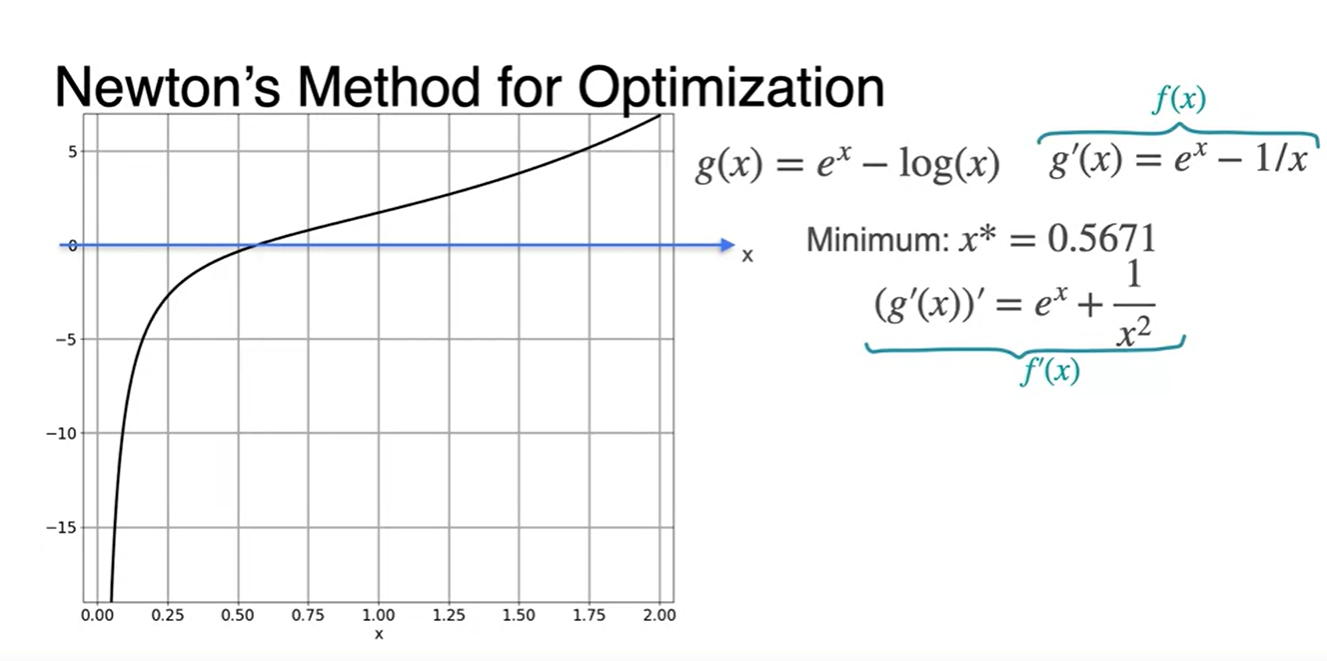
-
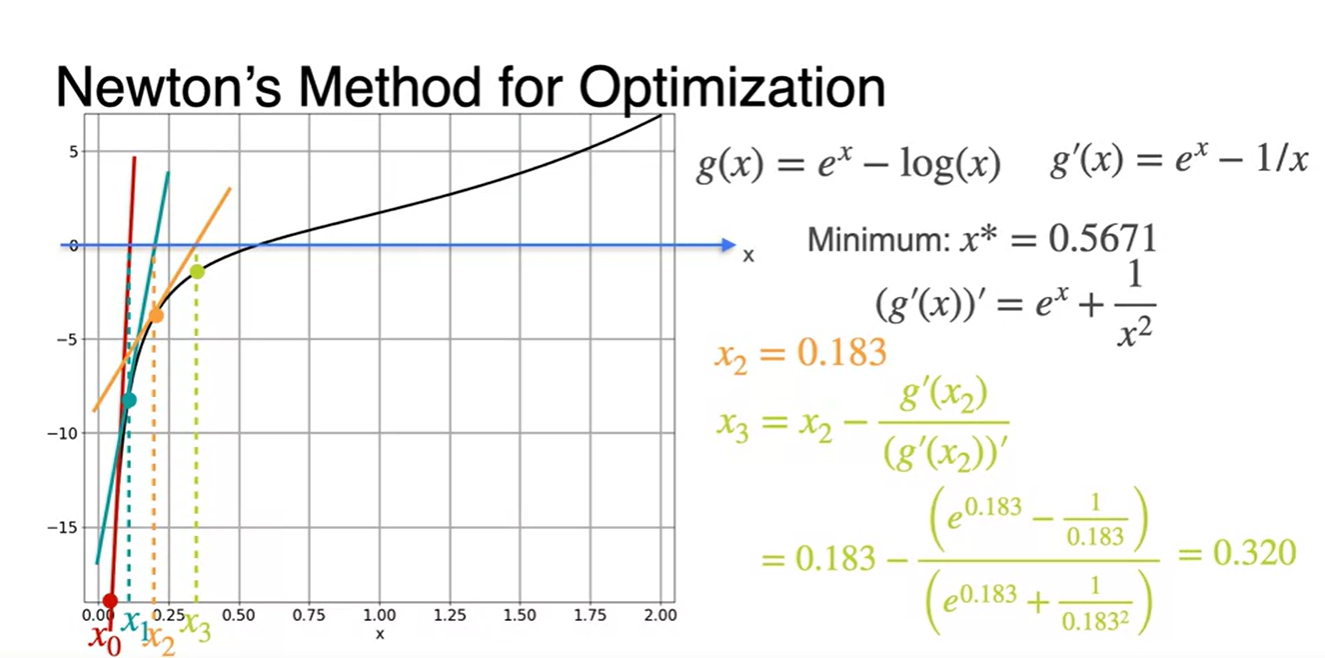
이제 초깃값 를 대입해보자.
- 에 대입하여 다음 값을 찾는다.
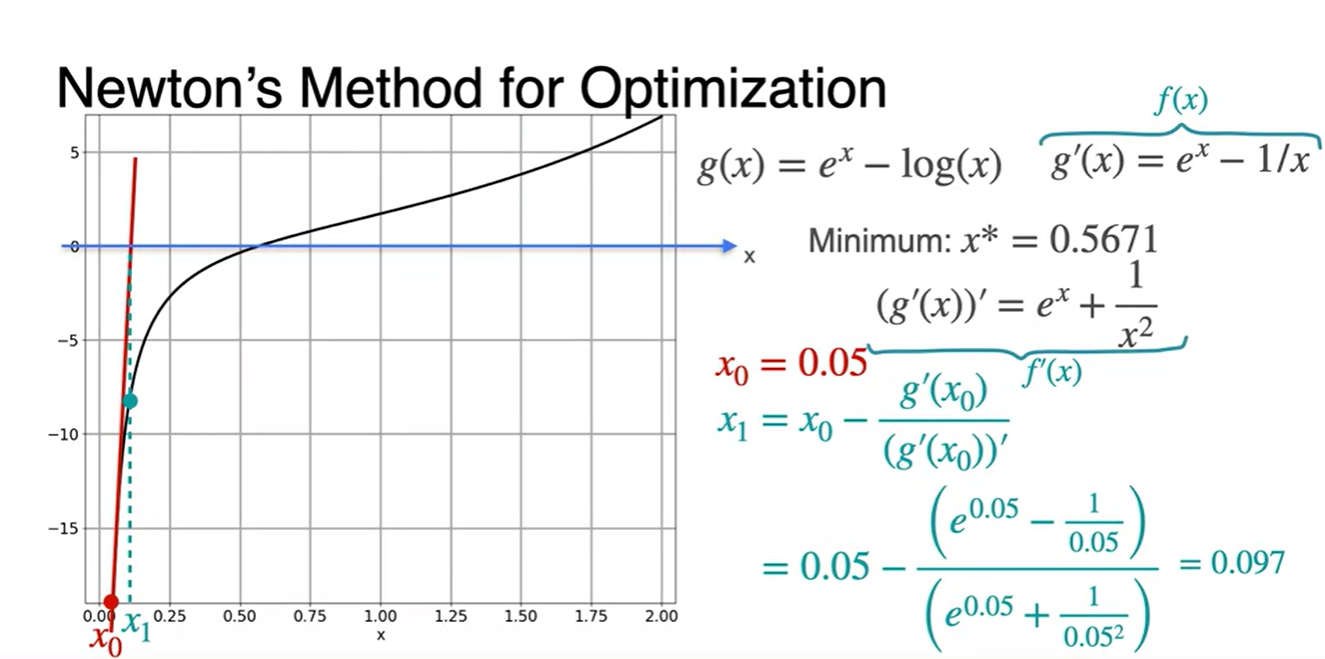
-
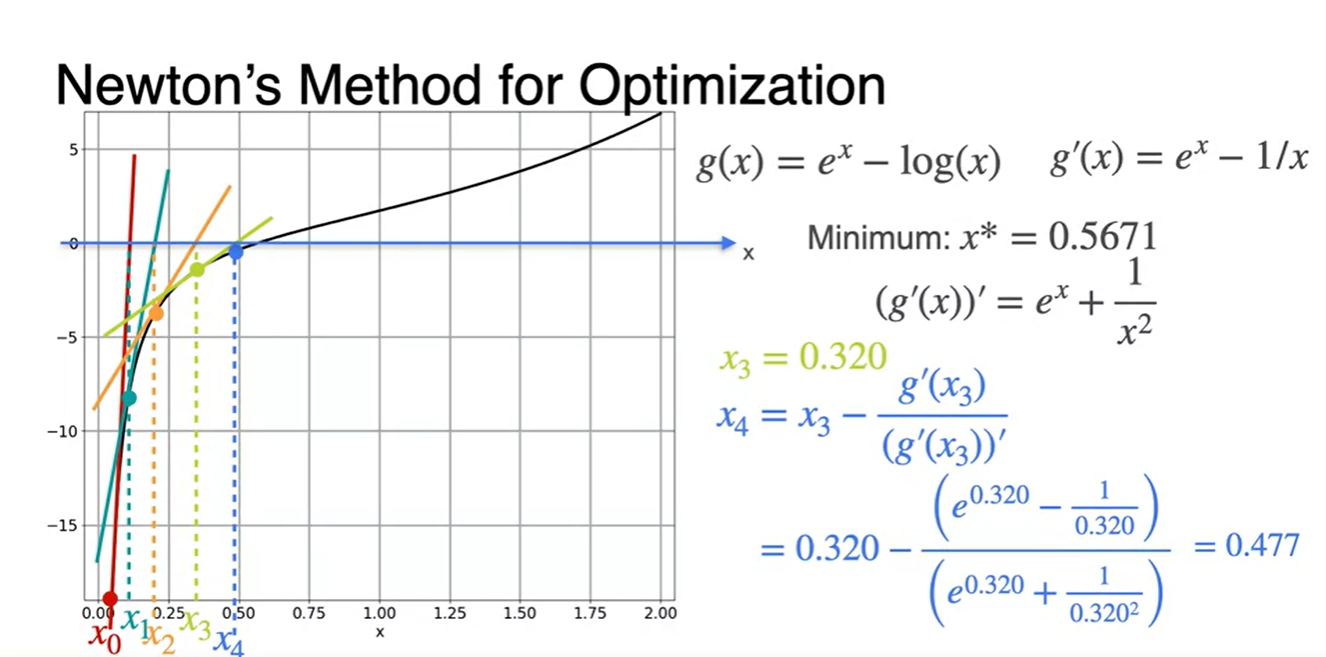
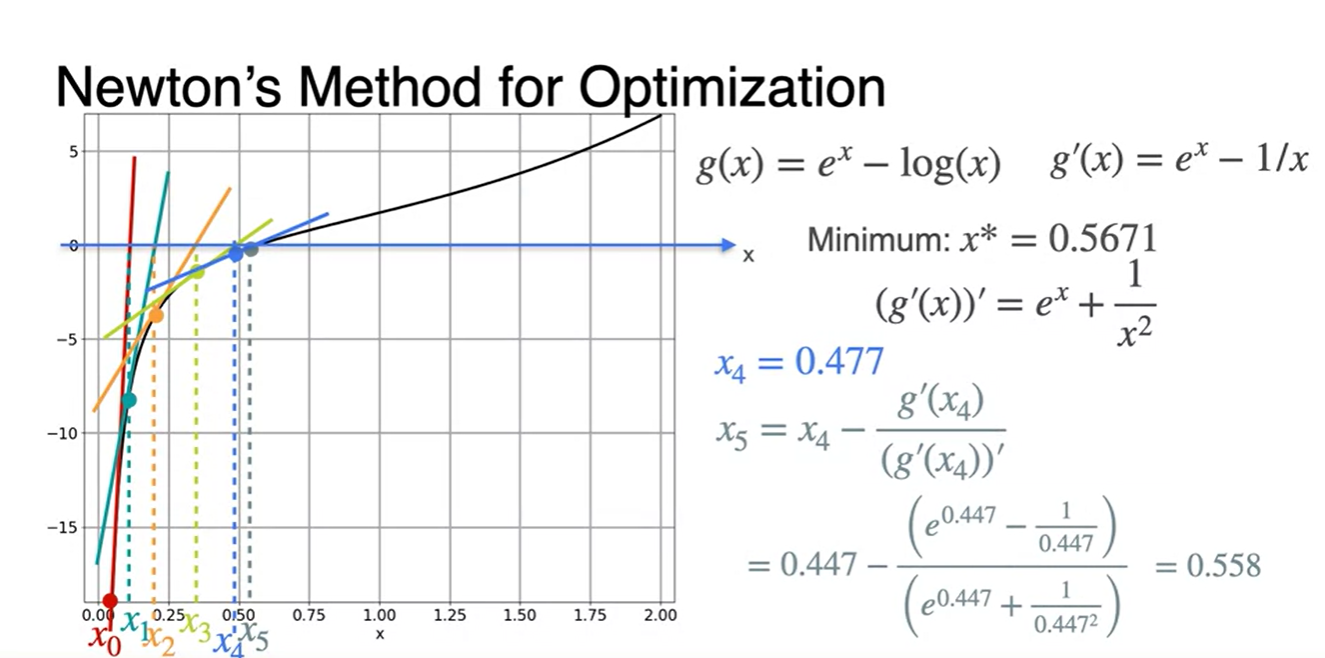
위에서 구해진 값을 통해 다시 한 번 값을 찾는다.
- 에 대입하여 다음 값을 찾는다.

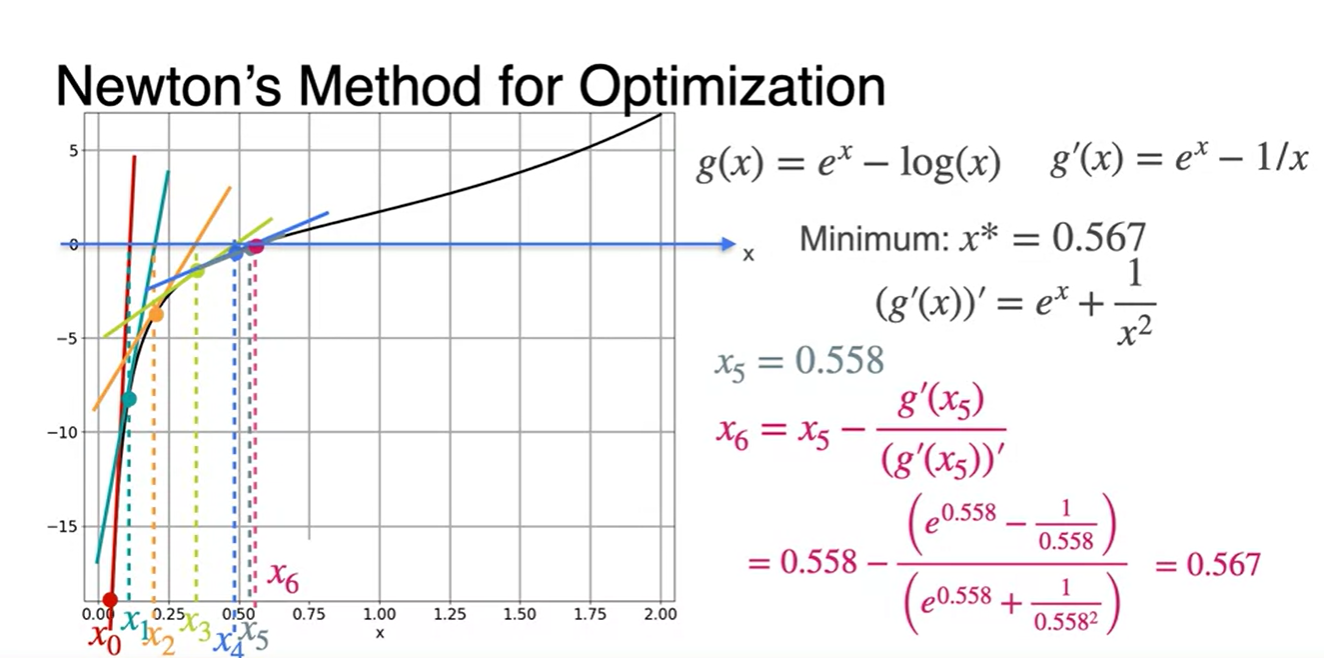
- 같은 과정을 계속해서 반복한다.
-
그러다보면 어느 순간의 지점에서 x값이 계속해서 비슷한 값으로 업데이트 될 것이다.
- 그러한 지점에서 break를 걸어 Loss를 minimize하는 최종 parameter x를 찾는다.
The second derivative
-
Second Derivative, 이계도함수에 대해 알아보자.
-
라이프니츠 notation으로는 ,
-
라그랑지안 notaion으로는 로 표현한다.
-

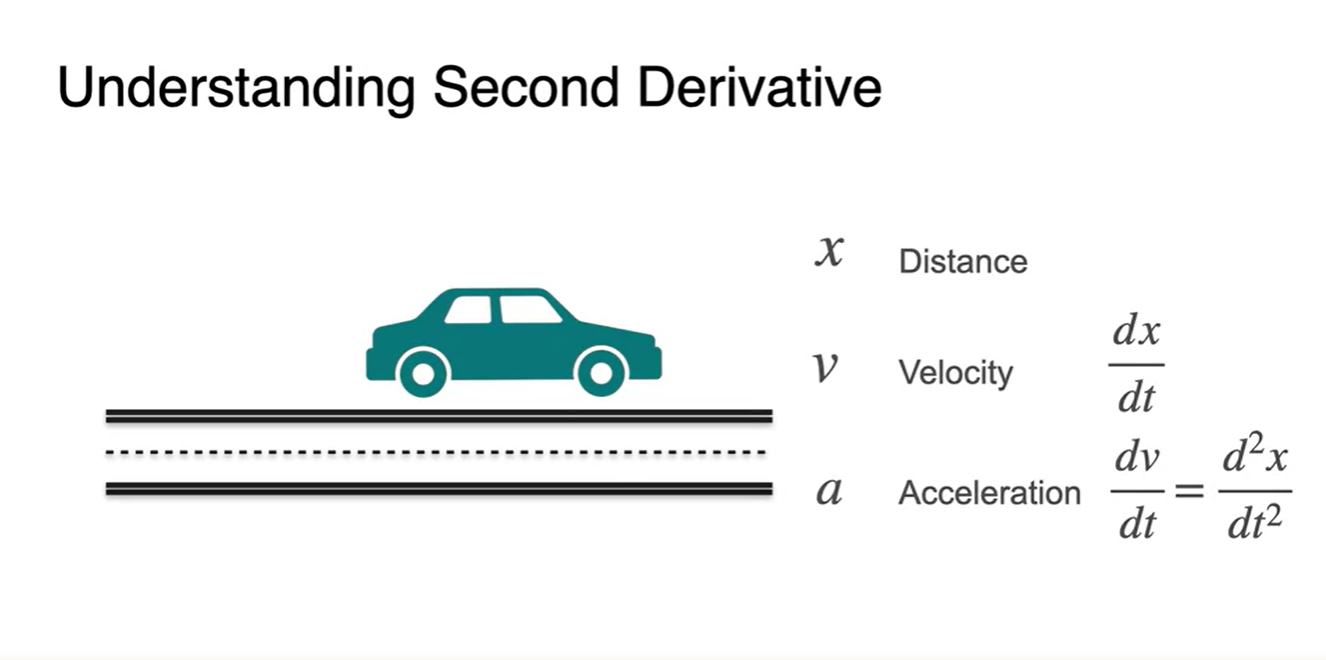
- 는 distance(위치), 는 velocity(속도), 는 acceleration(가속도)다.
-
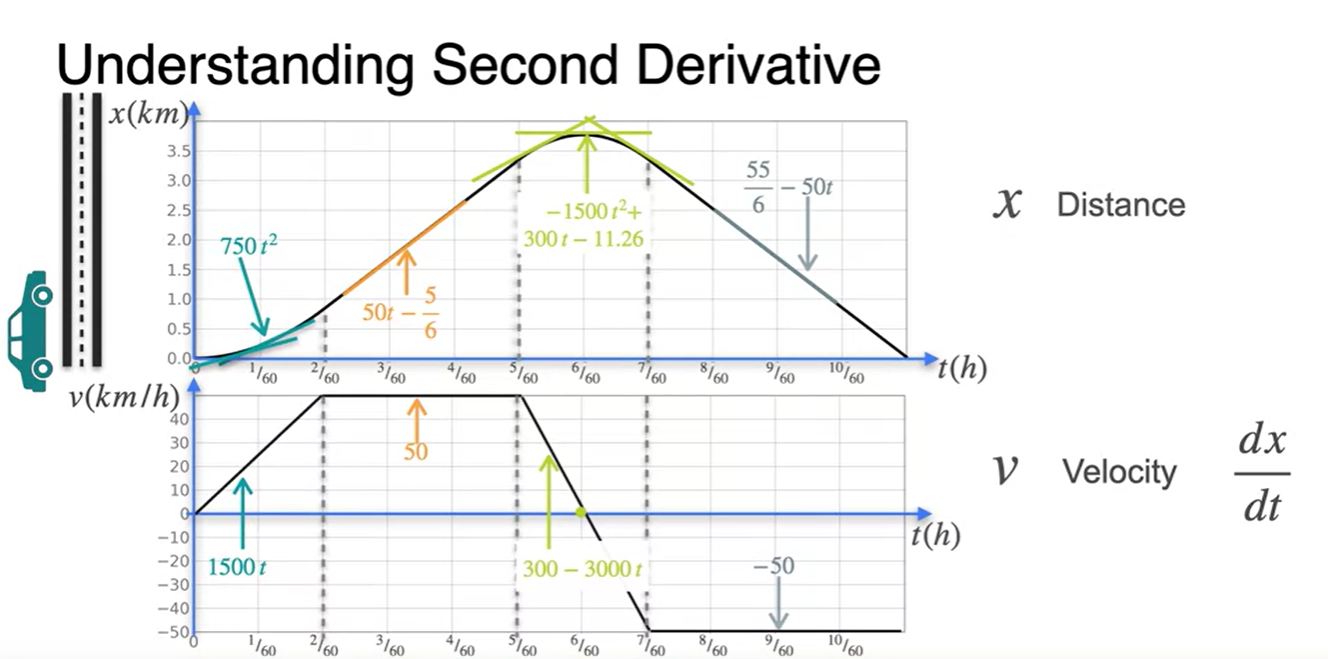
시간 에 대한 함수로 표현된 위치 함수 와 속도 함수 관계는 이렇다.
-
즉, 위치 함수 의 slope(미분량)을 시간에 따라 점 찍으면 속도 함수가 된다.
- 구체적으로는 {각 구역으로 나눈 위치 함수}의 미분 도함수가 {속도 함수}로 표현되는 것이다.
-
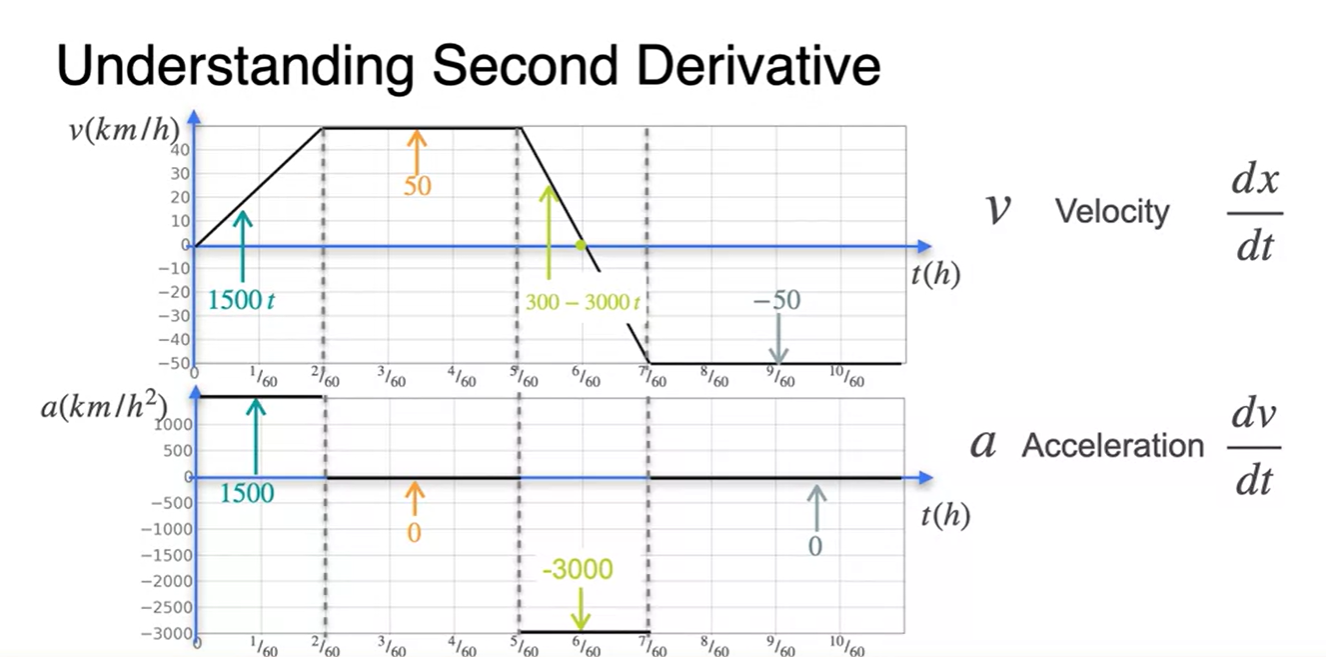
-
가속도 함수는 속도 함수 의 미분 도함수다.
- {각 구역으로 나눈 속도 함수}의 미분 도함수가 {가속도 함수}로 표현되는 것이다.
-
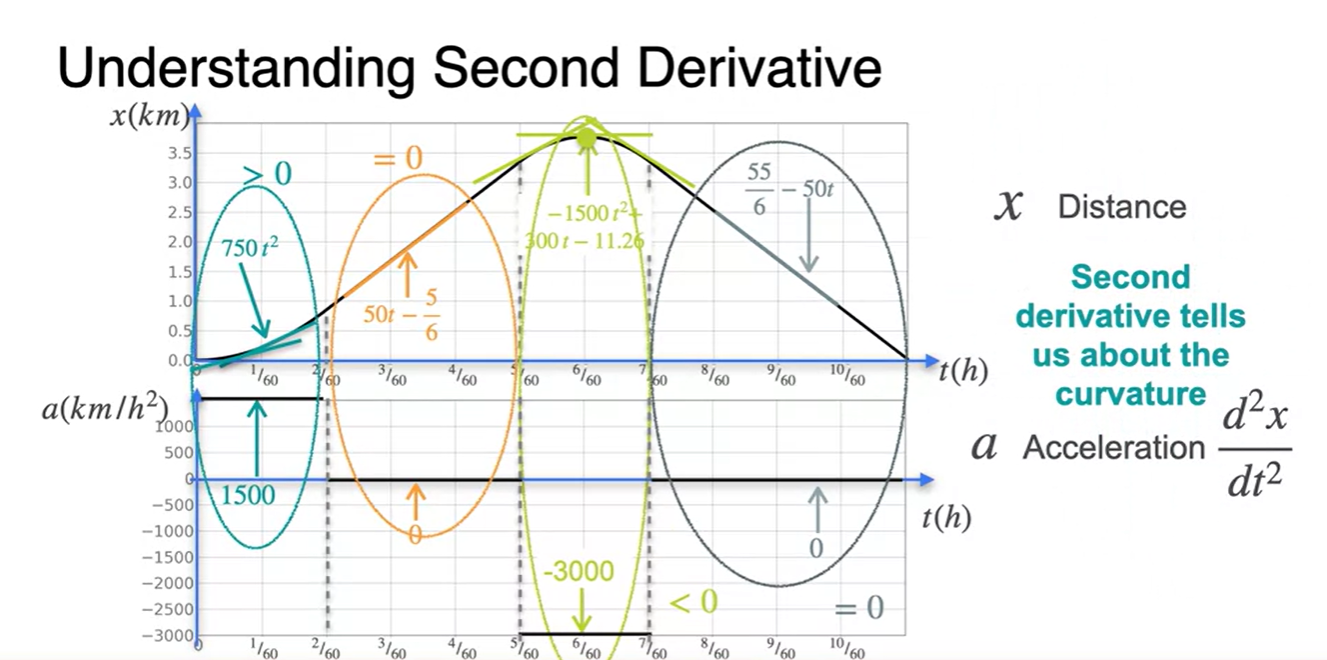
위치 함수 와 가속도 함수 의 관계는 이렇다.
-
각 구간별로 나누어 살펴보면 오목한 함수는 이계도함수가 > 0, 볼록한 함수는 이계도함수가 < 0인 것을 특징적으로 알 수 있다.
-
위치의 변동성이 일정한 즉, 속도 변화가 상수인 구간의 이계도함수는 = 0 이다.
-
-
이를 영어로는 Curvature라고 하는데, convex function이면 Concave up & 그 반대면 Concave down이라 볼 수 있다.
-
이계도함수가 0인 것만으로는 어떠한 정보도 얻어낼 수 없다.
- 예를 들어, 2차 미분량의 앞뒤 부호가 다르다는 조건이 주어진면 변곡점이라는 특징이 존재하기도 한다.
-
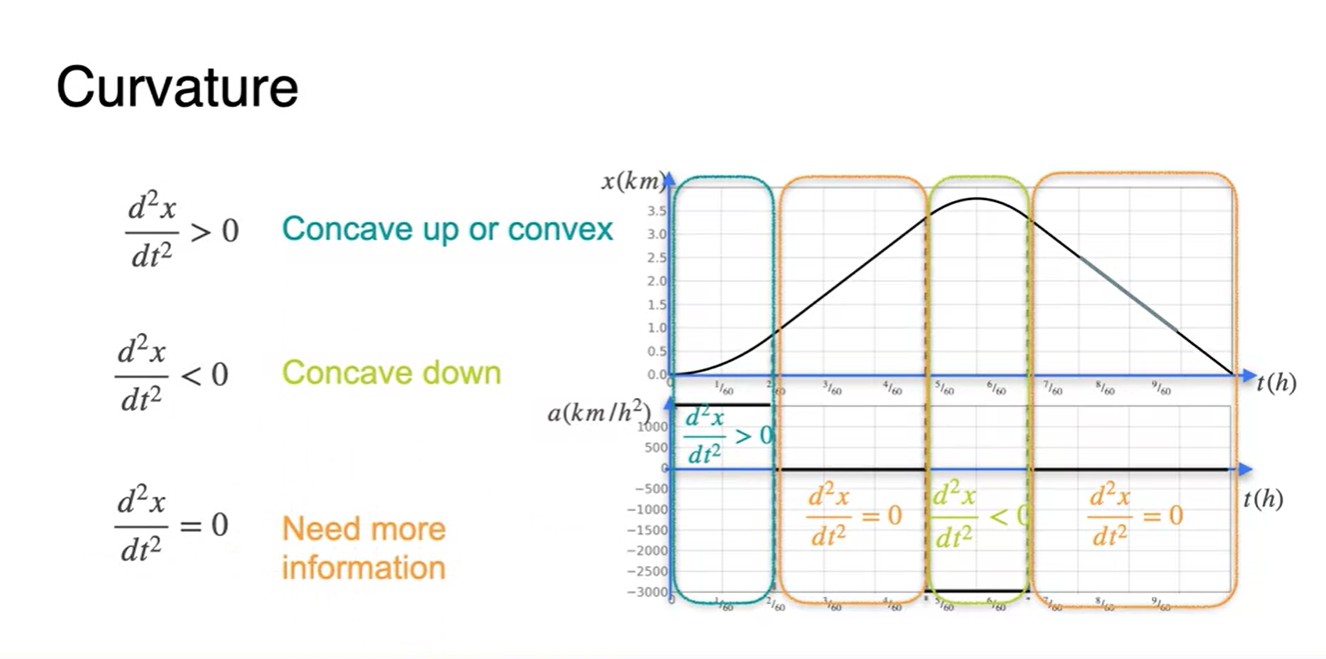
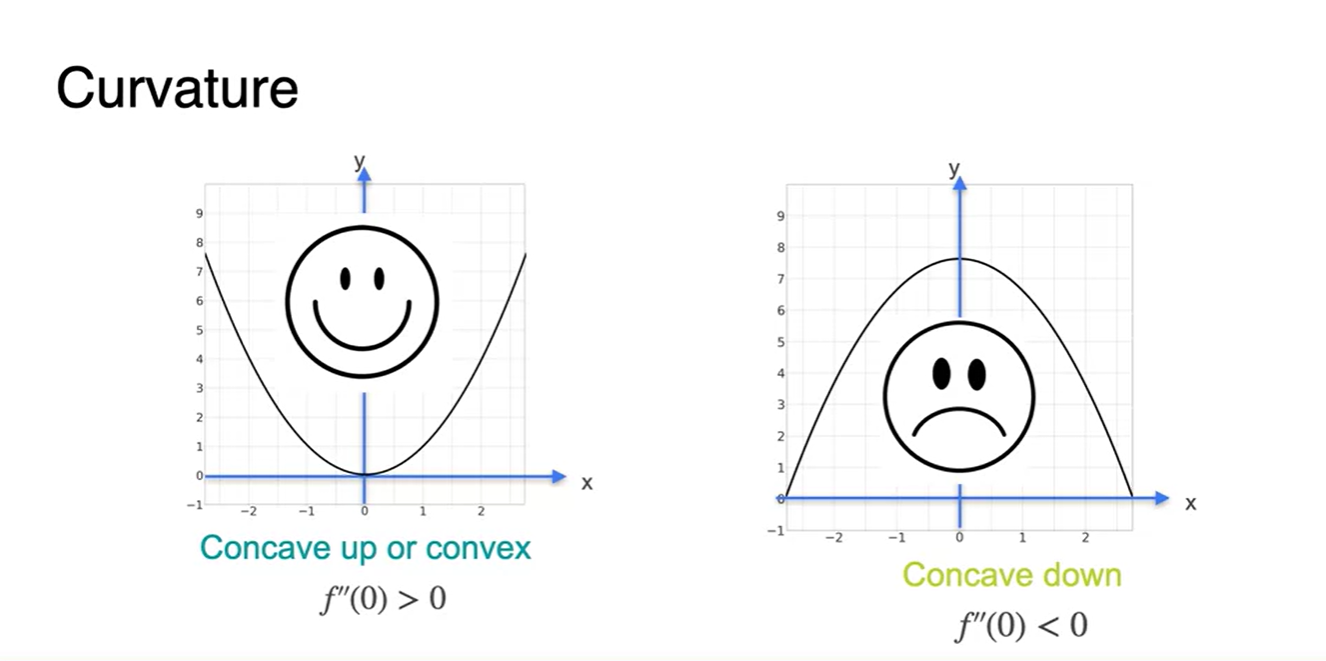
- 함수 모양을 쉽게 구별하기 위해 웃는 얼굴이면 > 0, 찡그린 얼굴이면 < 0로 생각하자.
-
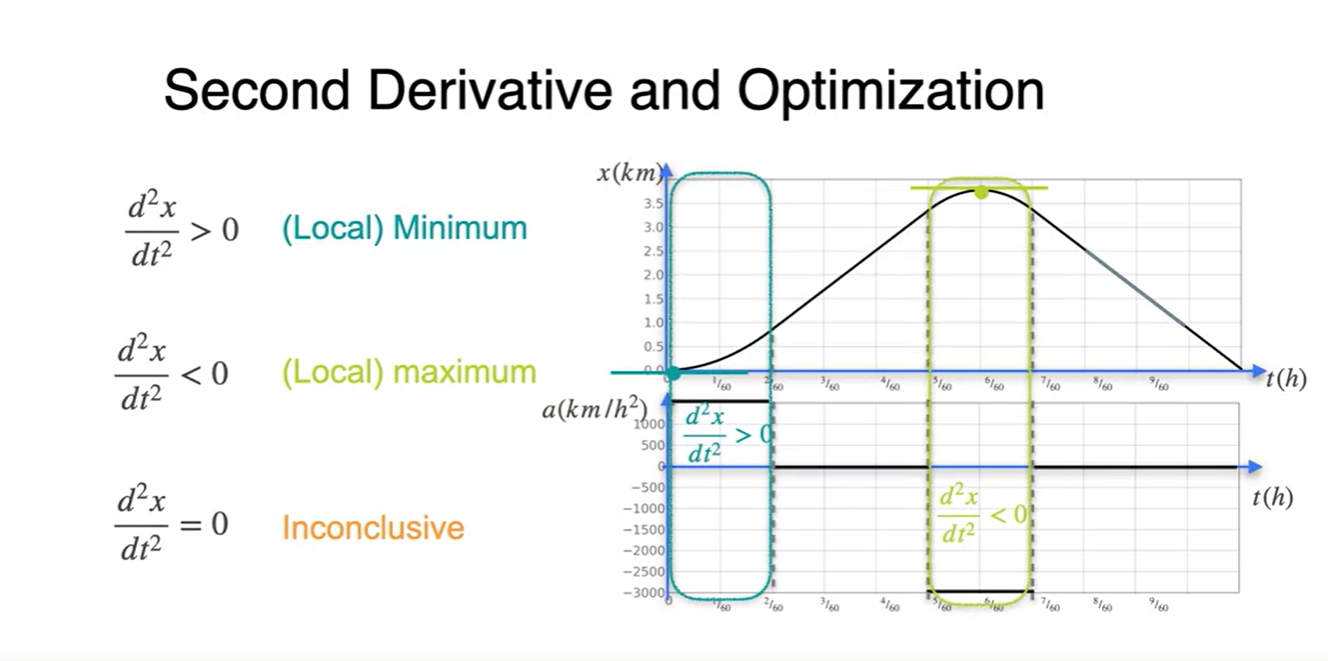
Loss function의 2차 미분 함수가 > 0인 구간이면 (Local) Minimum이라는 것을 기억하자.
- 반대로 2차 미분 함수가 < 0이면 (Local) Maximum, 0이면 어떠한 구간도 아니다.
The Hessian
-
변수가 1개일 때와 2개일 때의 차이를 표로 정리해보자.
-
1차원 함수 는 변수로만 미분한 함수이기 때문에 라고만 나타내었다.
-
2차원 함수 는 , 변수로 각각 편미분 해준 함수를 벡터화하여
로 표현한다.
- 그럼 의 2차 미분의 형태는 어떤 모양을 하게 될까?
-

-
함수를 2차 미분까지 이어가보자.
-
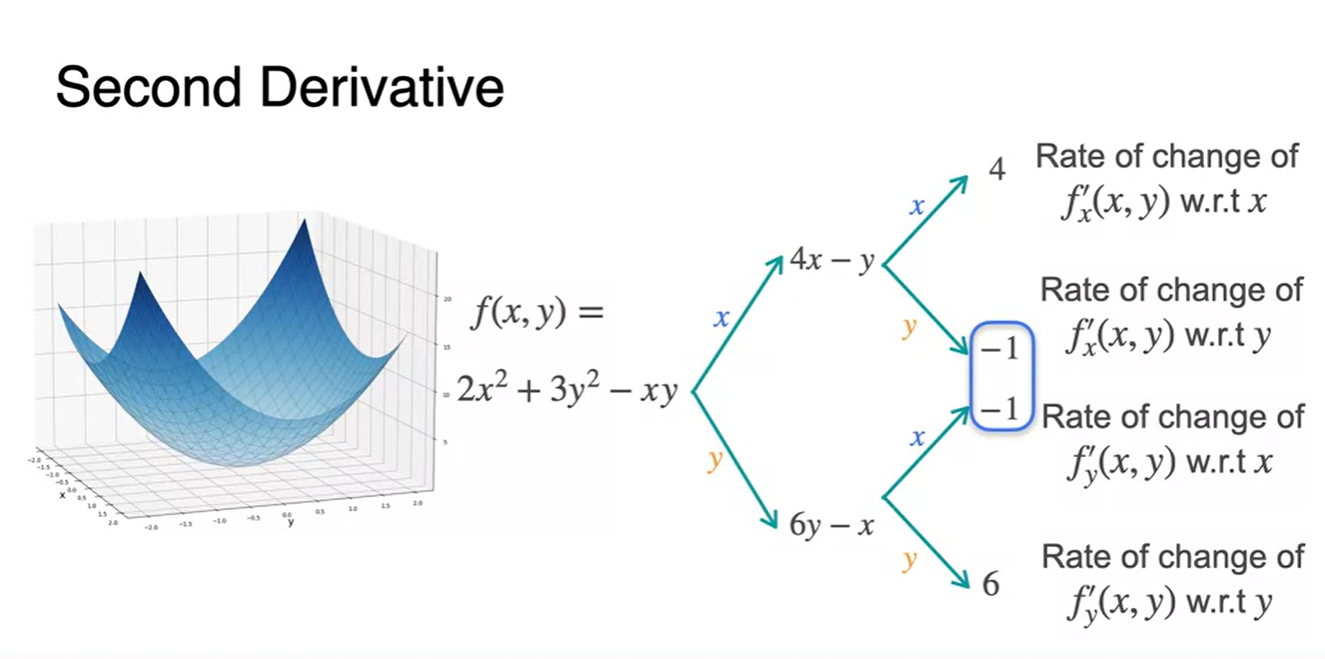
변수로 미분한 와 변수로 미분한 함수를 얻는 과정까지는 1차 미분이었다.
- 1차 도함수를 또 다시 와 로 한번 더 미분하면 4, -1 / -1, 6의 미분 함수(상수 함수)가 얻어진다.
-
-
이러한 과정을 하는 이유는 무엇일까?
-
{변화량 함수}의 변화량(Change in the change)을 와 변수 각각에 대해 살펴보고 싶기 때문이다.
- 각 변수가 orthogonal 하다면 와 로 각각 한번씩 미분한 함수는 똑같은 과정으로 취급하며, Symmetric한 과정이라고 이해하면 된다.
-

- 라이프니츠 notation과 라그랑지안 notation의 차이는 아래와 같다.

-
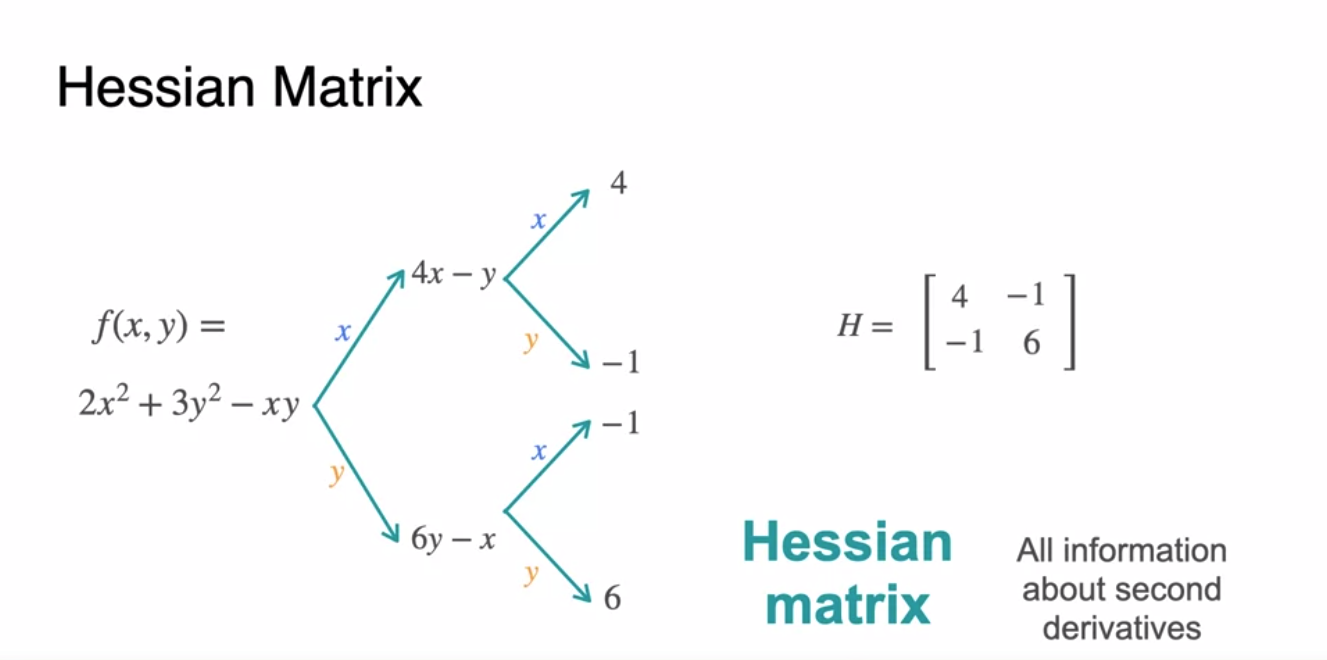
Hessian 행렬은 2차 미분 도함수를 행렬화 한 형태를 나타낸다.
- 1행 1열은 에 대한 2번 미분,
1행 2열은 로 1번 & 로 1번 미분,
2행 1열을 로 1번 & 로 1번 미분(1행 2열과 같다),
2행 2열은 에 대한 2번 미분
- 1행 1열은 에 대한 2번 미분,
-
라그랑지안 notation을 써서 수식으로 표현하면 다음과 같다.
- 로 표현한다.

- 앞서 살펴 보았던 표에 Hessian 행렬을 넣어 완성해보자.

Hessians and concavity
-
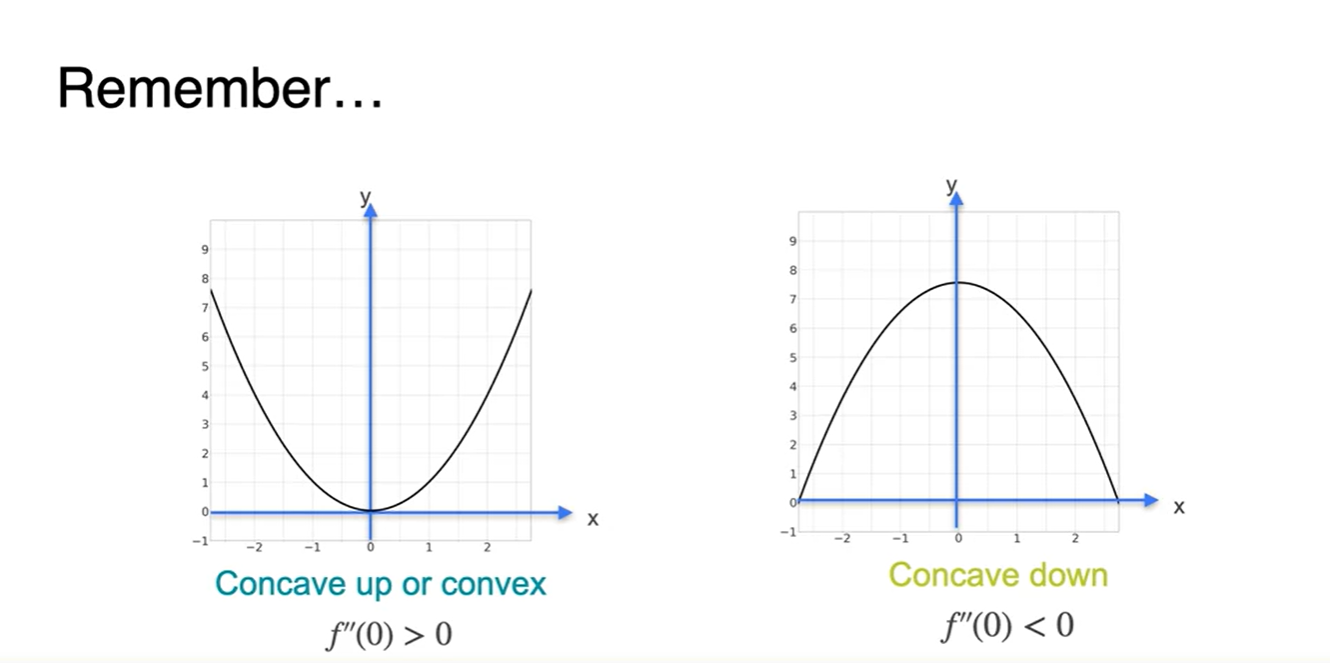
2차 미분이 양수인 것과 음수인 것의 차이는 Concave up or down으로 설명할 수 있었다.
- 이면 오목한 함수, 이면 볼록한 함수다.
-
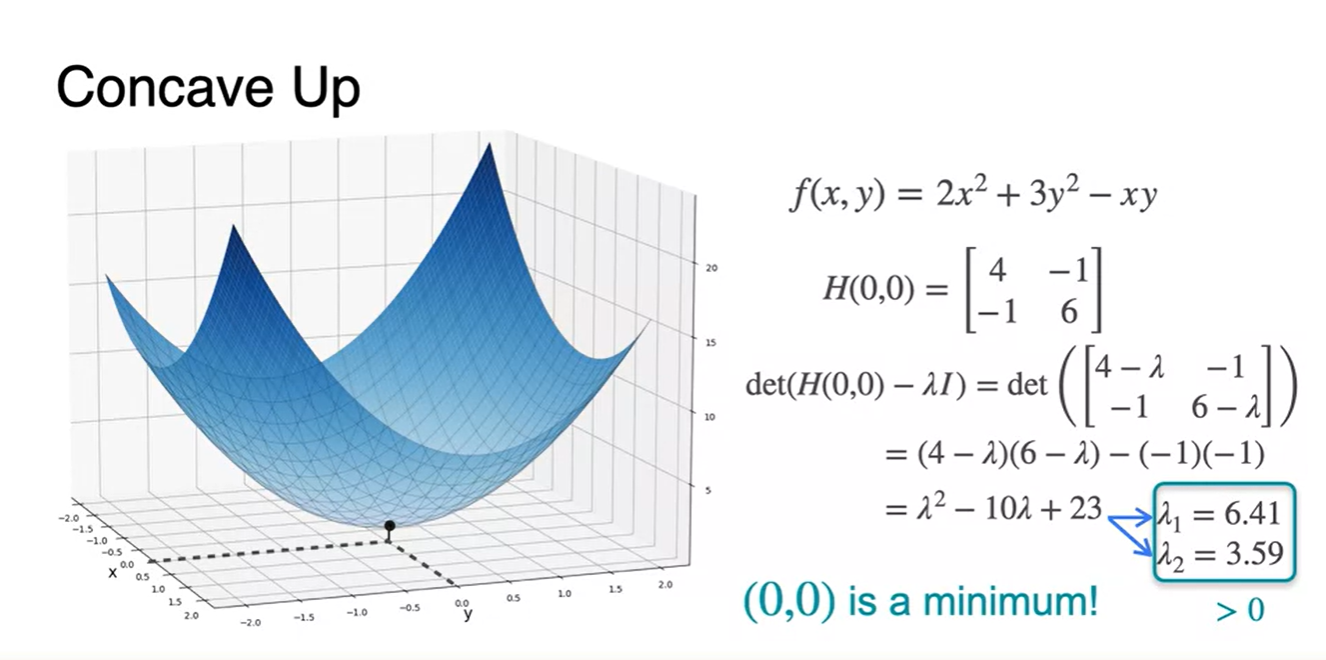
Concave up 함수의 Hessian 행렬이 구해졌다면 eigenvalues를 구해봄으로써 함수의 모양을 예측할 수 있다.
-
특정 지점에서의 Hessian 행렬의 eigenvalues가 모두 양수라면 해당 함수의 모양은 오목한 함수이며 해당 지점에서 minimum한 값을 가진다.
- Eigenvalue 형이 왜 여기서 나와..
-
-
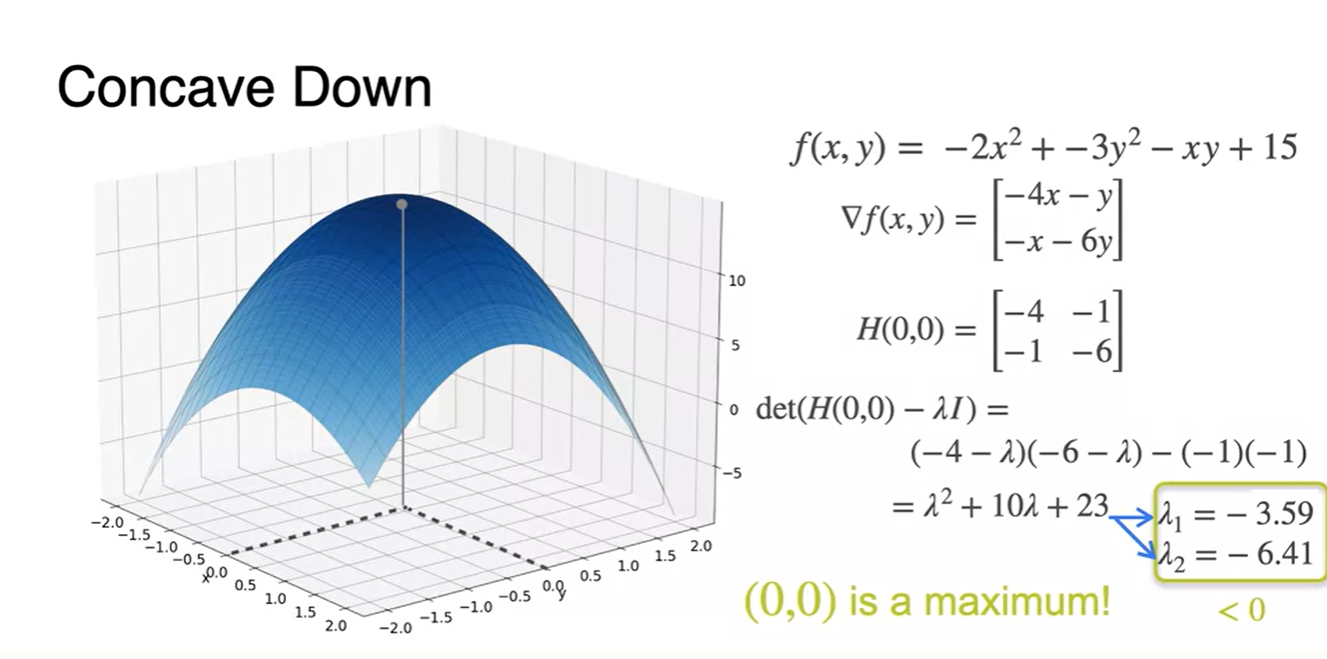
반대로 Concave down 함수에서의 Hessian 행렬을 구하여 eigenvalues를 구해보면 모두 음수임을 알 수 있다.
-
이를 통해 그 지점에서 함수는 볼록한 함수임을 알 수 있고 해당 지점이 바로 maximum이라는 점 또한 알게 된다.
-
이처럼 특정 parameters에서의 Hessian 행렬과 eigenvalues를 구했을 때 값이 모두 양수이거나 음수라면 해당 지점이 minimum / maximum 인지를 추측할 수 있다!
-
-
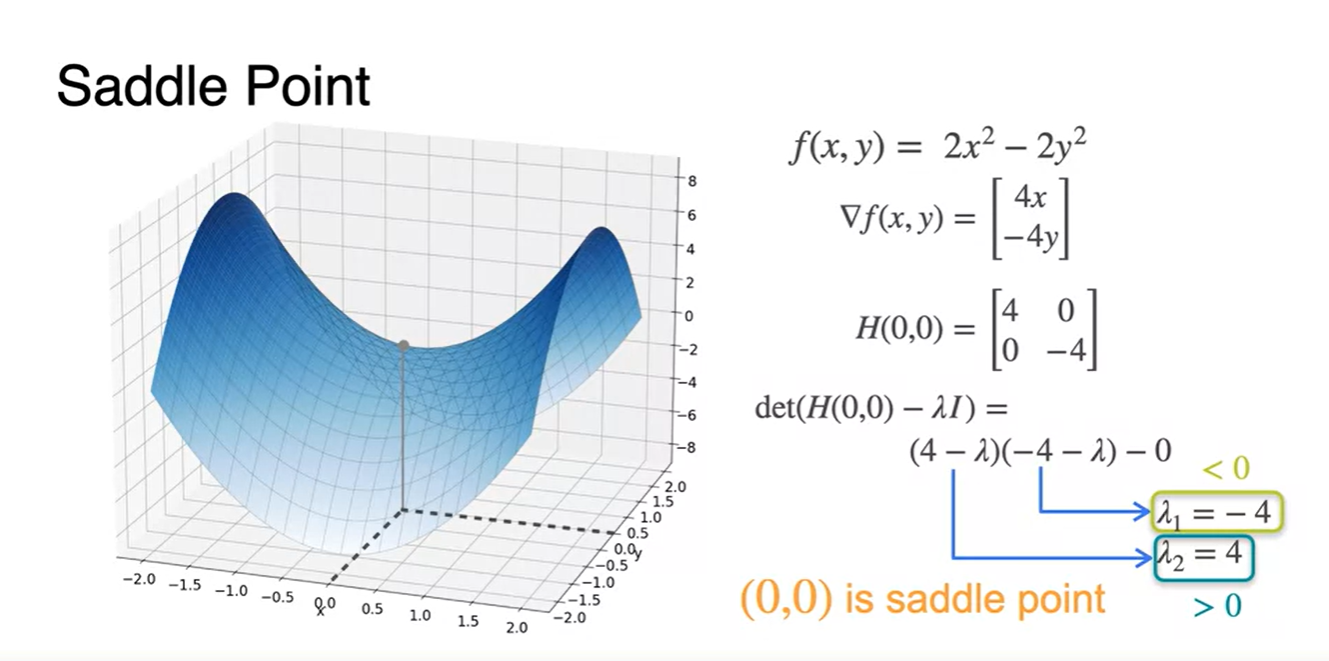
만약, Saddle Point(안장점)이라면 eigenvalue는 양수일 수도 있고 음수일 수도 있으며 어떠한 값은 0일 수도 있다.
-
Eigenvalue가 이차 미분의 값을 유추하게도 만드는건가 싶으나 이는 더 확인해봐야 할 듯 하다. (뇌피셜)
- 이렇게 생각한 이유는 안장점에서의 {2차 미분 = 0}이라는 일반적 상식이 존재하기 때문이다.
-
-
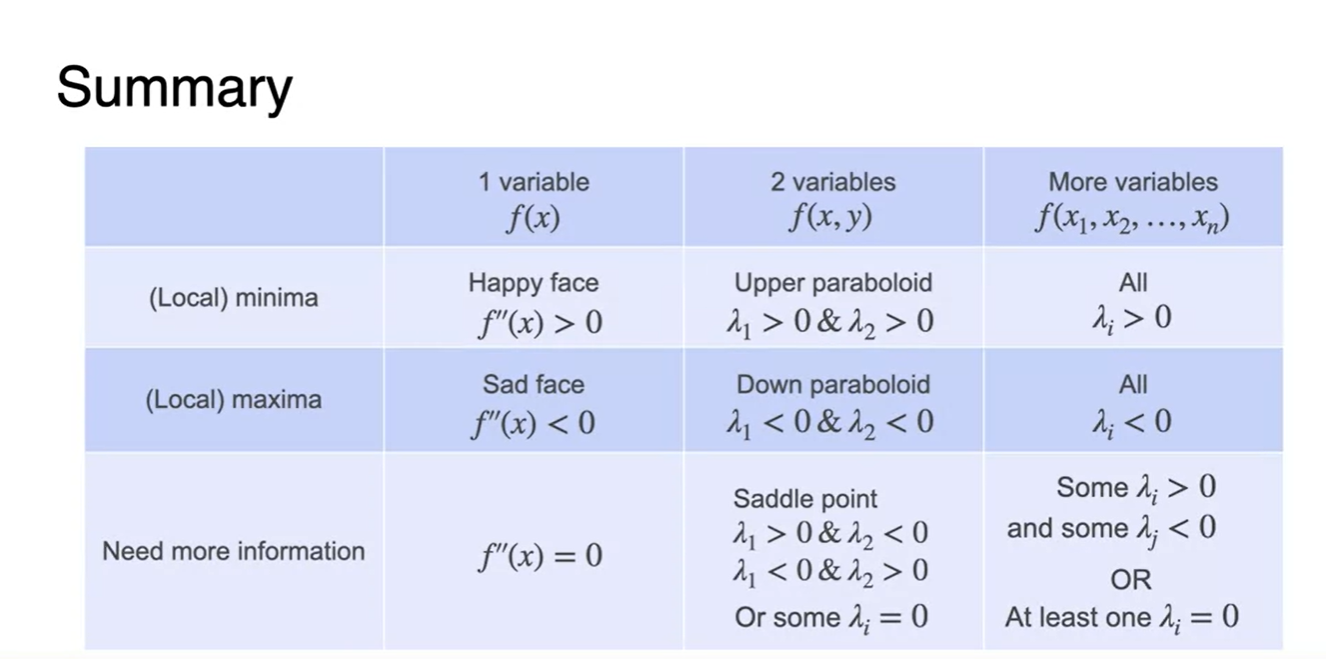
요약하자면 아래와 같다.
-
변수가 많아질 때에도 마찬가지로, 오목한 함수일 때의 eigenvalues는 모두 양수, 볼록한 함수일 때의 eigenvalues는 모두 음수다.
- 다시 말해, eigenvalues가 모두 양수인 지점이 바로 (Local) minima 지점이며 eigenvalues가 모두 음수인 지점이 바로 (Local) maxima 지점이다.
-
Newton's Method for two variables
-
이제 Hessian 행렬을 적용하여, 2 variables를 가질 때의 도함수가 0인 지점을 추정해보자.
-
기존 점화식을 다시 작성해보면 로 쓰여진다.
-
이를 행렬로 표현하면 2차 미분 도함수인 Hessian 행렬과 1차 미분 도함수 의 곱으로 표현할 수 있다!
-
-

-
과 의 순서를 절대로 바꿔서는 안 된다.
- 행렬 곱의 특성 상 (2x2)@(2x1)은 가능하지만 (2x1)@(2x2)는 불가하다.

- 함수의 Hessian 행렬을 찾기 위해 각 변수들로 미분하여 나타낸 결과가 아래와 같다.
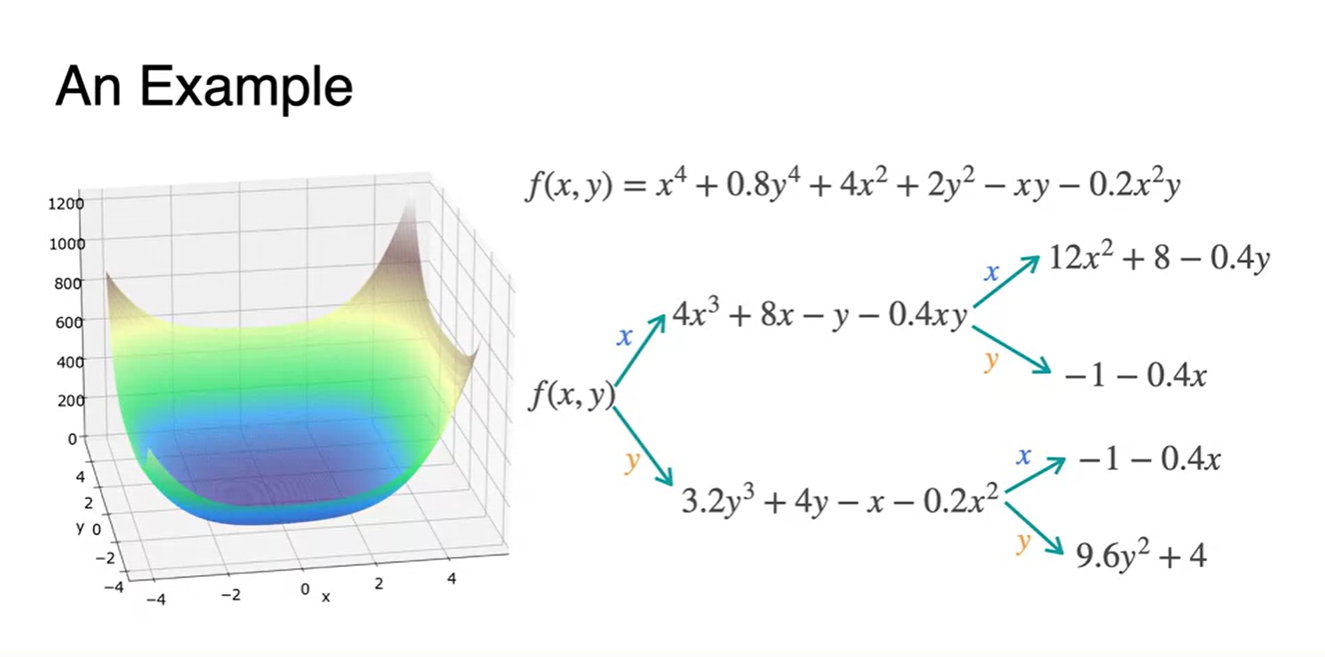
- 와 Hessian 행렬을 찾아 행렬로 쌓은 형태가 아래와 같다.
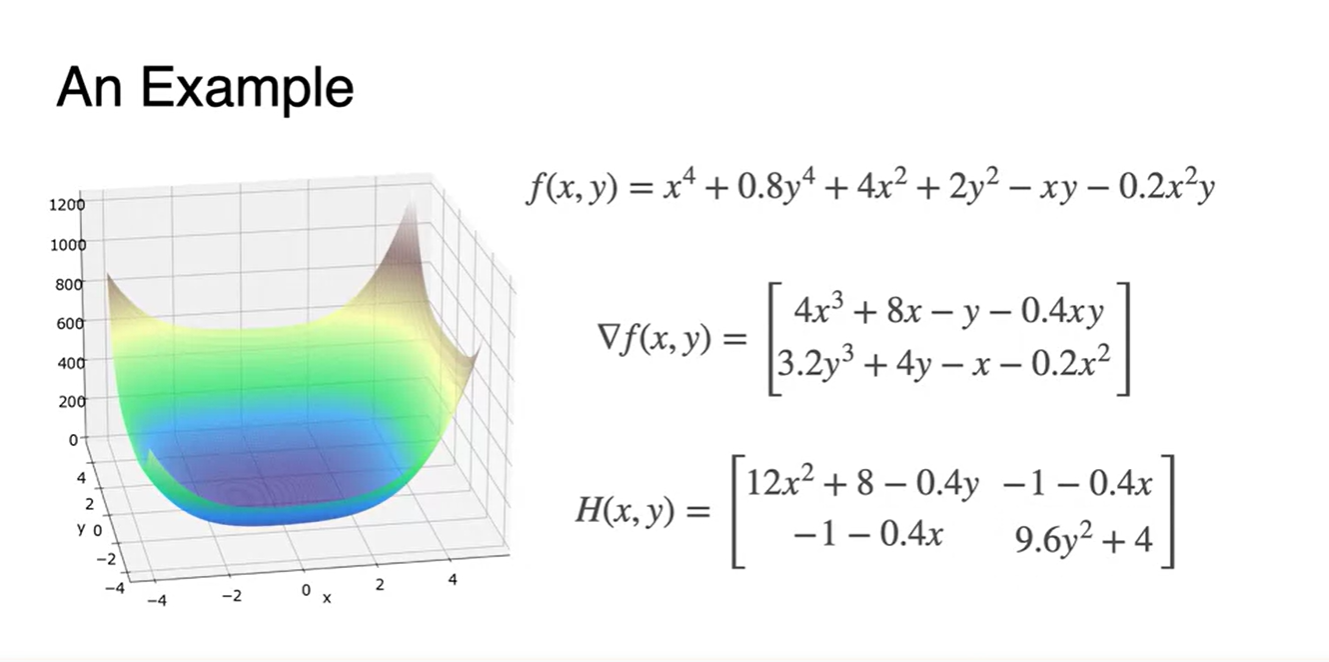
-
이제 본격적으로 stating point를 잡아 Newton's Method로 함수가 0인 지점의 parameter를 찾아가보자.
- 현재 starting point는 지점이다.
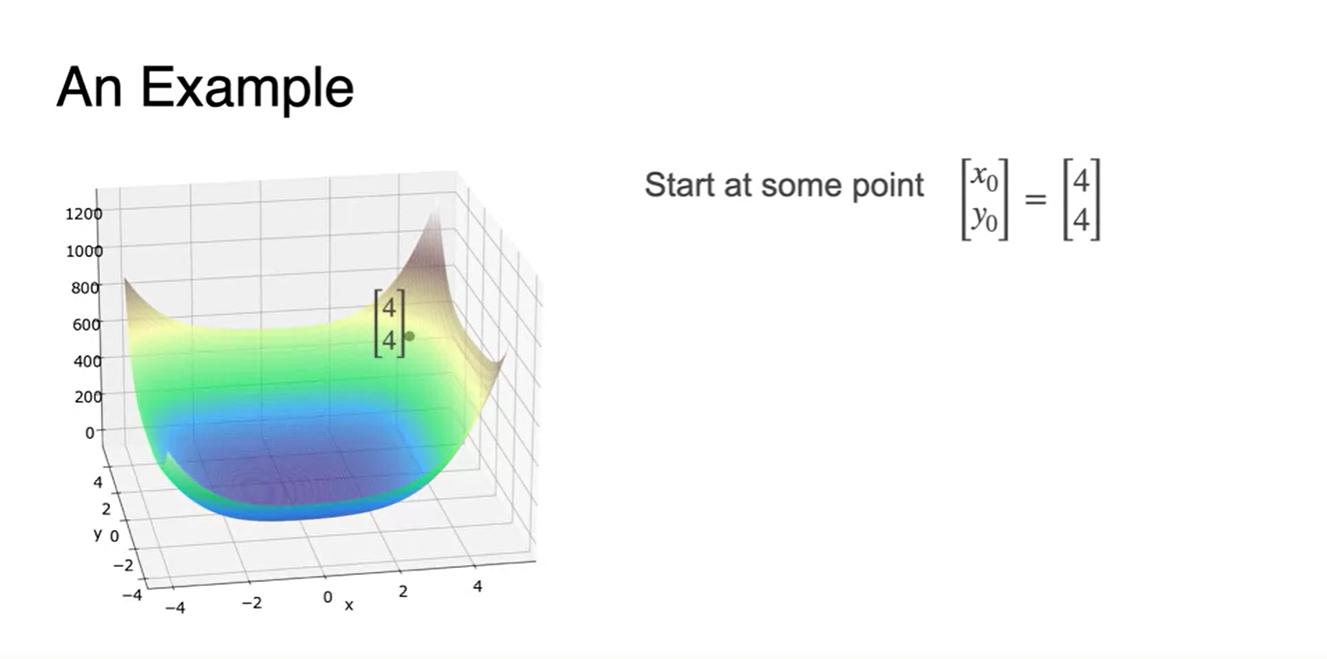
- 와 그리고 Newton's Method로 다음 parameter를 계산한 결과다.
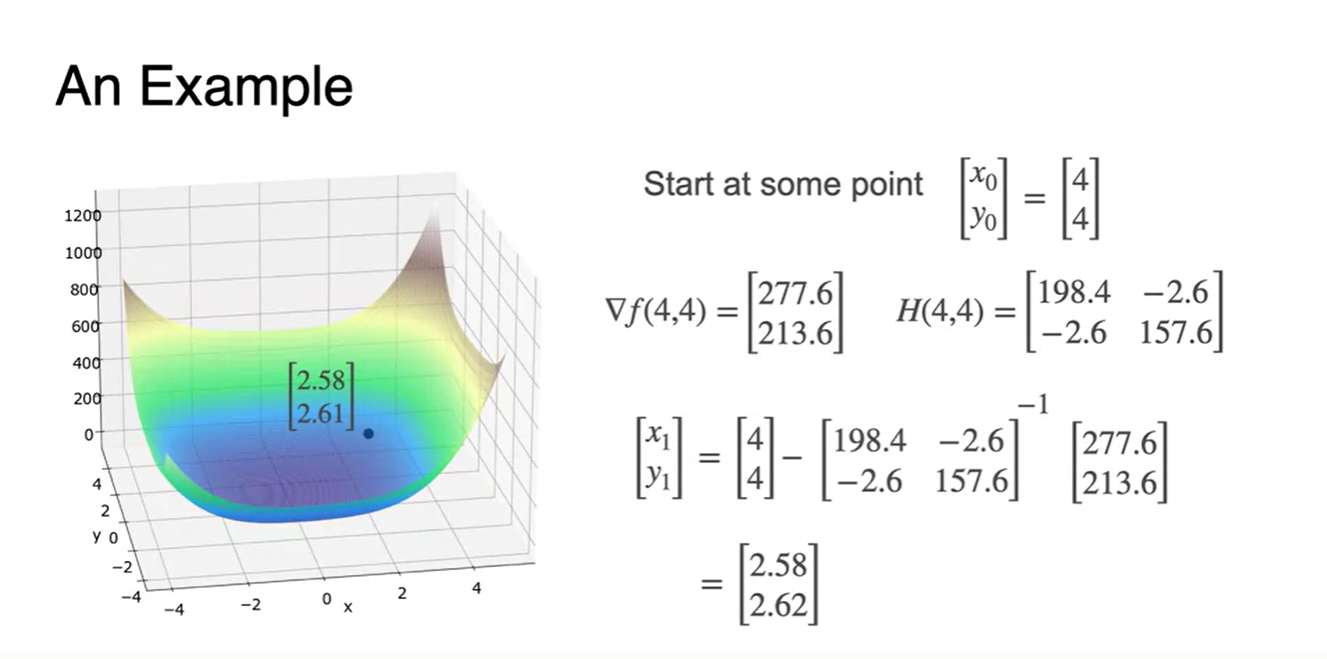
- 위에서 추정된 로 , 을 찾아, 다음 parameter를 추정한 결과다.
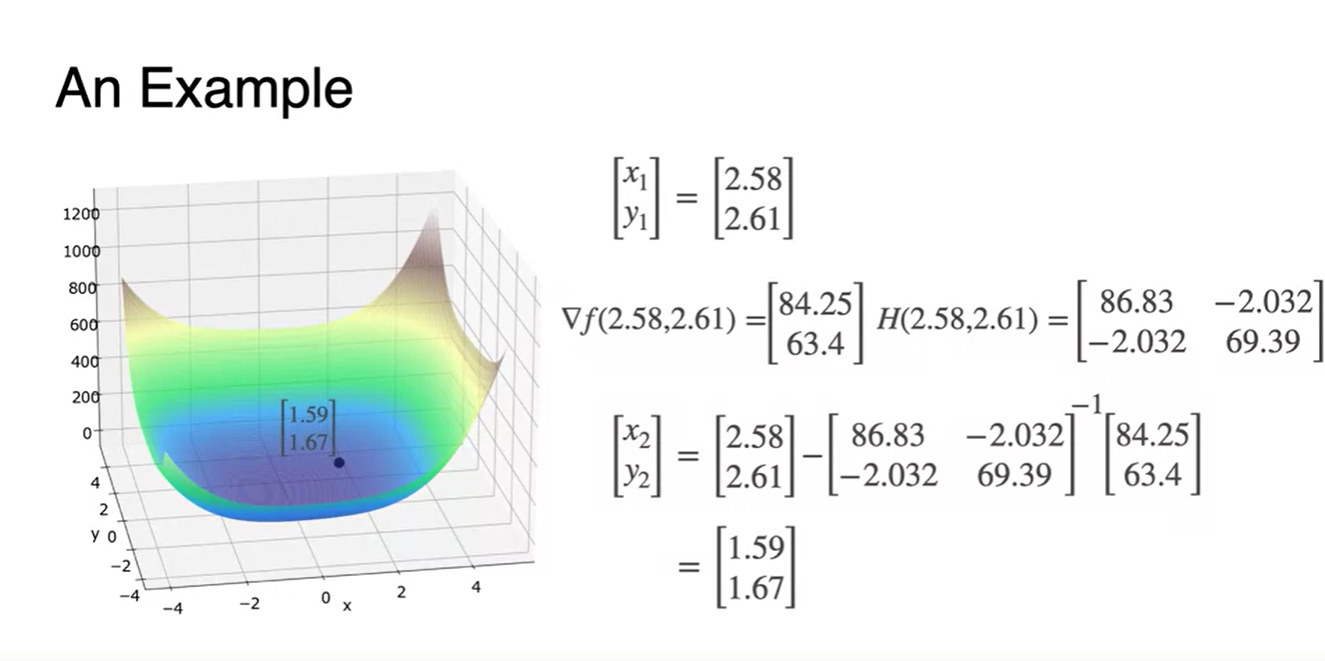
-
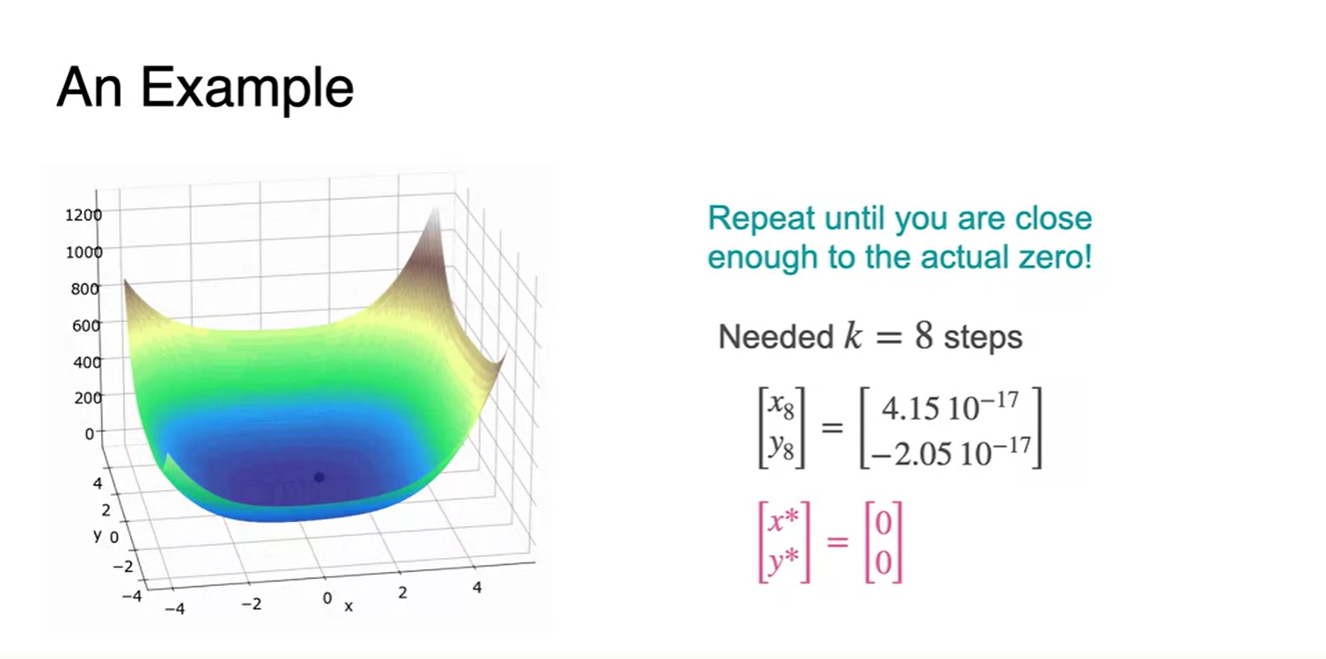
이러한 과정을 반복하다 보면 어떠한 지점에서 특정 값으로 수렴하는 구간이 찾아오게 된다.
-
현재는 8번째 step에서 의 값을 추정할 수 있었다.
- 이 지점이 바로 도함수를 0으로 만드는 즉, (Local) minima 지점의 parameter임을 알 수 있다.
-